Module 2.0 - NumPy Arrays

Objectives

The goal of this module is to introduce numpy arrays, for use when working with numeric data.

2.0.0 A List of Lists

Recall a basic list:

# A list of integers:
evens = [2, 4, 6, 8, 10]

# A list of strings:
greetings = ['hello', 'hi', 'howdy', 'aloha']

# Access list elements using square brackets and index
x = evens[1] + evens[3]
print(x)

# We can change the value at an individual position
evens[0] = x

# Recall: len() gives us the length of the list
print('length:', len(evens), 'contents:', evens)

# Example of using **in** to search inside a list:
if (not 'hey' in greetings):
    print('missing hey')

# Add something new to the end of a list
evens.append(12)

# Write code here to increment each element by 2

print(evens)
# Should print: [12, 4, 6, 8, 10, 12]

Exercise 2.0.1

First, in list_example.py, type up the above to see what it prints (without including the missing code). Then, in list_example2.py, add the missing code to increment each list element by 2.

Let’s recall a few things we learned about lists via this example:

list features

Why are lists useful? - Using a loop to create elements, as in:

for i in range(1, 10, 2):
        A.append(2*i)

Performing some action on each element, as in:

for i in range(len(A)):
        A[i] = 2 * A[i]

One can use multiple lists as well, as in:

for i in range(len(A)):
        B[i] = A[i] + 5

Lists allow both index iteration as above but also content iteration:

total = 0
    for k in A:
        total = total + k

As it turns out, we can make a list of lists.

That is, a list whose elements are themselves lists.

For example:

A = [ [2,4,6,8,10], [1,3,5,7,9] ]

x = A[1]          # The 2nd element is a list
print(x)          # Prints [1,3,5,7,9]

y = A[1][3]       # 4-element of 2nd list
print(y)          # 7

print(len(A))     # 2
print(len(A[0]))  # 5

The inner square brackets are used for the two lists contained in the one larger list:

list of lists

And the outermost square brackets indicate the single list with two items:

list of lists

A[1] refers to the 2nd element of the outer list, which means A[1] is the 2nd inner list
Since A[1] is a list itself, we can access its elements using an additional set of square brackets, e.g., A[1][3] = 7
And the len() function applied to the whole list will give 2, while applying it to one of the constituent lists will give that list’s length

Exercise 2.0.2

Consider the following code:

A = [[1,2,3,4], [4,5,6,7], [8,9,10,11,12]]
x = A[?][?]
print(x)     # Should print 7

# Write code to increment every element using a nested `for` loop:


print(A)
# Output should be: [2, 3, 4, 5], [5, 6, 7, 8], [9, 10, 11, 12, 13]]

In list_example3.py, add the correct numbers to replace the question marks. Then, write a nested for loop to increment every element of every constituent list.

Think of a single list as one dimensional:

A = [2, 4, 6, 8, 10]
print(A[3])

In a one-dimensional list, we need a single number to access a data value in the list: print(A [3])

A list of lists is two dimensional:

A = [ [2,4,6,8,10], [1,3,5,7,9] ]
print(A[0][2])

In a two-dimensional list, we need two numbers to access a data value in the list:, hence print(A[0][2])

Think of a list of lists of lists as three-dimensional, which means three numbers fix the position of a element. For example:

A = [ [ [1,2], [3,4], [5,6] ], [ [7,8], [9,10], [11,12] ] ]

It’s a bit hard to see the list of lists of lists:

list of lists

We can look at indexing list elements by looking at each element:

Get the outermost element:

A = [ [ [1,2], [3,4], [5,6] ], [ [7,8], [9,10], [11,12] ] ]

print(A[0])

[[1, 2], [3, 4], [5, 6]]

Get the third element of the outermost element:

A = [ [ [1,2], [3,4], [5,6] ], [ [7,8], [9,10], [11,12] ] ]

print(A[0][2])

[5, 6]

Get the second element of the third element of the outermost element:

A = [ [ [1,2], [3,4], [5,6] ], [ [7,8], [9,10], [11,12] ] ]

print(A[0][2][1])

2.0.1 NumPy Arrays: A Better List for Numbers

Python was created as a general-purpose programming language and did not originally have support for numerical computing. A library called NumPy (numpy) was created to address this.

While lists are useful and easy to use, they are a bit inefficient “under the hood”:

Very large lists (million of elements or more) can slow down a program. A list-of-lists is even slower for large sizes, and takes up a lot of memory.

NumPy arrays (we will often call them simply “arrays”) were created as a separate structure in Python to enable efficient processing of lists of numbers, especially multidimensional lists.

Some of the most compelling uses involve the array equivalent of a list-of-lists-of-lists: an image. As we will see, a color image will can be represented as athree dimensional array while a black-and-white image only requires a two-dimensional array.

Because arrays are part of NumPy and not a “built-in” part of Python, the syntax around arrays is a bit different, for example:

import numpy as np

A = np.array([1,2,3,4])

Arrays constitute a large topic in Python, and its advanced features can be fairly complex.
This is a basic introduction so that we can work with images.
Let’s start with an example of a one-dimensional array, the cousin of a plain list:

import numpy as np

A = np.array([1,2,3,4])

print(type(A))             # What does this print?
A[1] = 5                   # Replace 2nd element
print(A)                   # [1 5 3 4]
print(A.shape[0])          # 4
print('len(A)=',len(A))    # 4

# A[4] = 9
# A.append(9)

Exercise 2.0.3

Type up the above in array_example.py. Try un-commenting in turn each of the two commented-out lines at the end to see what kind of errors this yields. (Restore your program by commenting out both.)

Let’s point out a few things: To gain efficiency, arrays trade away some flexibility and ease of use. For example, we now need to import this special package called numpy:

import numpy as np

Once we do this, the syntax for making an array with actual data is, as we’ve seen:

A = np.array([1,2,3,4])

Why np ?

The convention to import the numpy library as np is strictly for convenience, using the keyword as to create a shortcut:

import numpy as np
A = np.array([1, 2, 3, 4])

This could also be written as:

import numpy
A = numpy.array([1,2,3,4])

There is no difference in the function of the code by creating the shorcut, but because we tend to use a lot of numpy arrays, the np shortcut saves time in writing code and makes the code more readable. It has become a convention in the Python/NumPy community, and you will rarely encounter import numpy without the np shortcut.

import numpy as np
A = np.array([1, 2, 3, 4])

Notice that that actual data is fed into the numpy``array function as a list:

import numpy as np
A = np.array([1, 2, 3, 4]) # [1, 2, 3,4] is the argument for np.array()

The actual array so created is assigned to the variable A. To work with elements in the array, we use square brackets with the variable A, just like a list:

A[1] = 5                   # Replace 2nd element

The standard function len() also works the same as with lists:

print('len(A)=',len(A))

However, the array has a feature that is more general called shape:

print(A.shape[0])          # 4

At first this seems cumbersome, and for single-dimensional arrays, it is.
But for multiple dimensions, it’s convenient to have the length of each dimension handy. This is what shape has.
shape[0] has the first dimension (the length of the array along the first dimension).
shape[1] has the length along the second dimension, and so on.
For a single dimensional array, there’s only shape[0].
One of the efficiency tradeoffs is that an array has a fixed size. This means to add a new element, we have to rebuild the array. Thus, to add an element in the above example, we need to write:

A = np.append(A, 9)
print(A)        # [1 5 3 4 9]

This creates a new array with the added element. The difference between what we have done here and modifying a list in place is subtle, but important. Typically most scientific applications do not change sizes on the fly, and so, this is not a serious restriction.

Numpy has powerful features that simplify manipulation of numeric arrays.

For example, consider:

import numpy as np

A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

C = A + B            # Direct element-by-element addition
print(C)             # [5, 7, 9]

D = np.add(A, B)     # The same, via the add() function in numpy
print(D)             # [5, 7, 9]

E = B - A            # Elementwise subtraction
print(E)             # [3, 3, 3]

Exercise 2.0.4

Type up the above in array_example2.py and add a line that multiplies the arrays A and B element-by-element, and prints the result: ([ 4 10 18]).

Exercise 2.0.5

In list_version.py, let’s remind ourselves about how lists work. Start by examining what happens with:

X = [1, 2, 3]
Y = [4, 5, 6]
Z = X + Y
print(Z)          # What does this print?

# Write code here to compute Z as element-by-element addition
# of X and Y (to give [5, 7, 9])

print(Z)

Then add code to perform element-by-element addition.

Numpy also has a number of functions that act on arrays and return arrays, for example:

One can apply a function like square-root element-by-element:

A = np.array( [1, 4, 9, 16] )
B = np.sqrt(A)
print(B)        # [1. 2. 3. 4.]

Numpy can create an array with random elements, as in:

# Roll a die 20 times
A = np.random.randint(1, 7, size=20)

This produces an array of size 20 with each element randomly chosen from among the numbers 1,2,3,4,5,6.
Numpy has its own random-generation tool: np.random This has a function randint() that takes the desired range (inclusive of first, excluding the last), and the desired size of the array.

One can also test membership using the in operator: For example, suppose we roll a die 20 times and want to know whether a 6 occured:

# Roll a die 20 times
A = np.random.randint(1, 7, size=20)  
if 6 in A:
    print('Yes, there was a 6')

Exercise 2.0.6

In dice_problem.py fill in code below to estimate the chances that you get a total of 7 at least once when rolling a pair of dice 10 times.

successes = 0
num_trials = 1000
for n in range(num_trials):
    # Fill your code here

print( successes/num_trials )

To do so, generate one array called A of length 10 with random numbers representing one die (selected from 1 through 6). Then generate a second array called B that represents the 10 rolls of the second die. A success occurs when A[i]+B[i] is 7 for some i. Can you solve this without accessing individual array elements with a loop?

2.0.2 2D Arrays

Here, 2D is short for two-dimensional. Let’s begin with a conceptual depiction of a 1D (one-dimensional) array:

First, suppose we create an array of 5 numbers as in:

A = np.array([50, 55, 60, 65, 70])

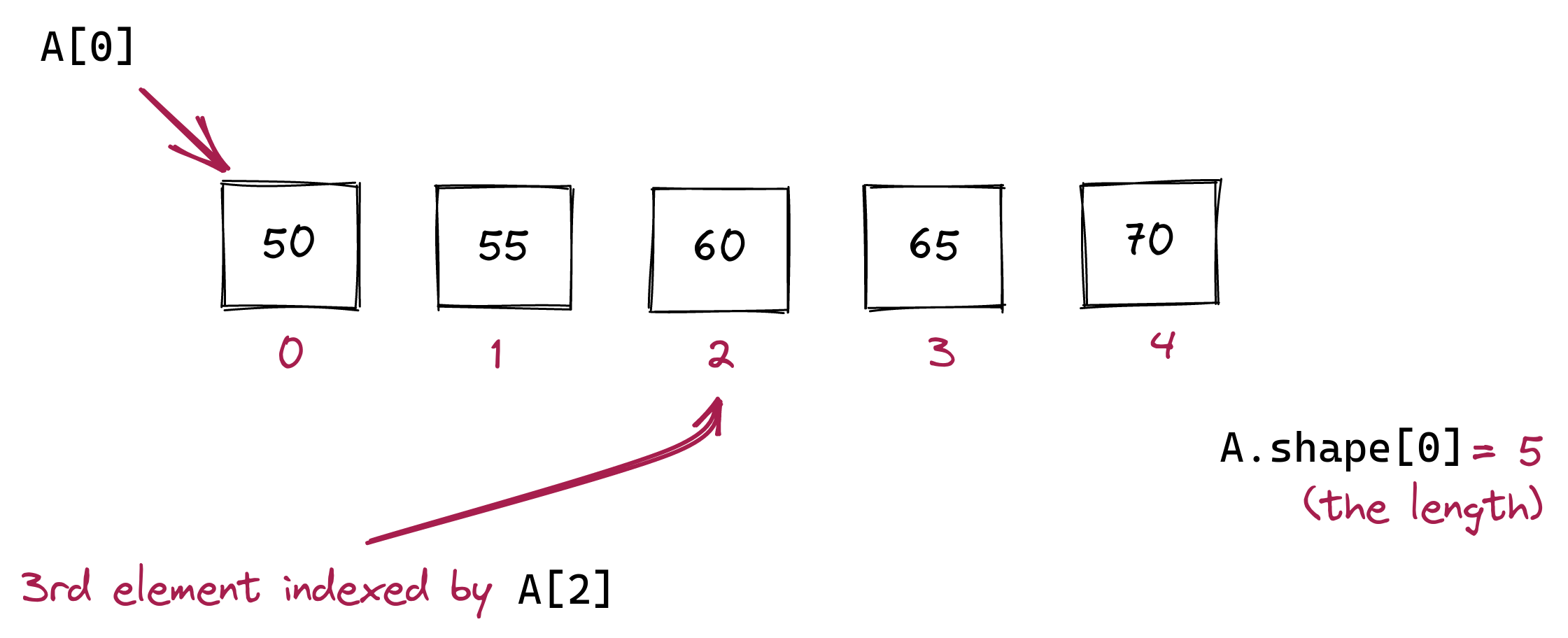
A convenient way to visualize this is to draw these numbers in a series of adjacent “boxes” as in:

boxes

Because we need a way to use our keyboard to enter elements, we use a particular kind of syntax, comma-separation with square-brackets to specify the elements. We use a similar type of syntax to access a particular element in this array, as in:

print(A[2])

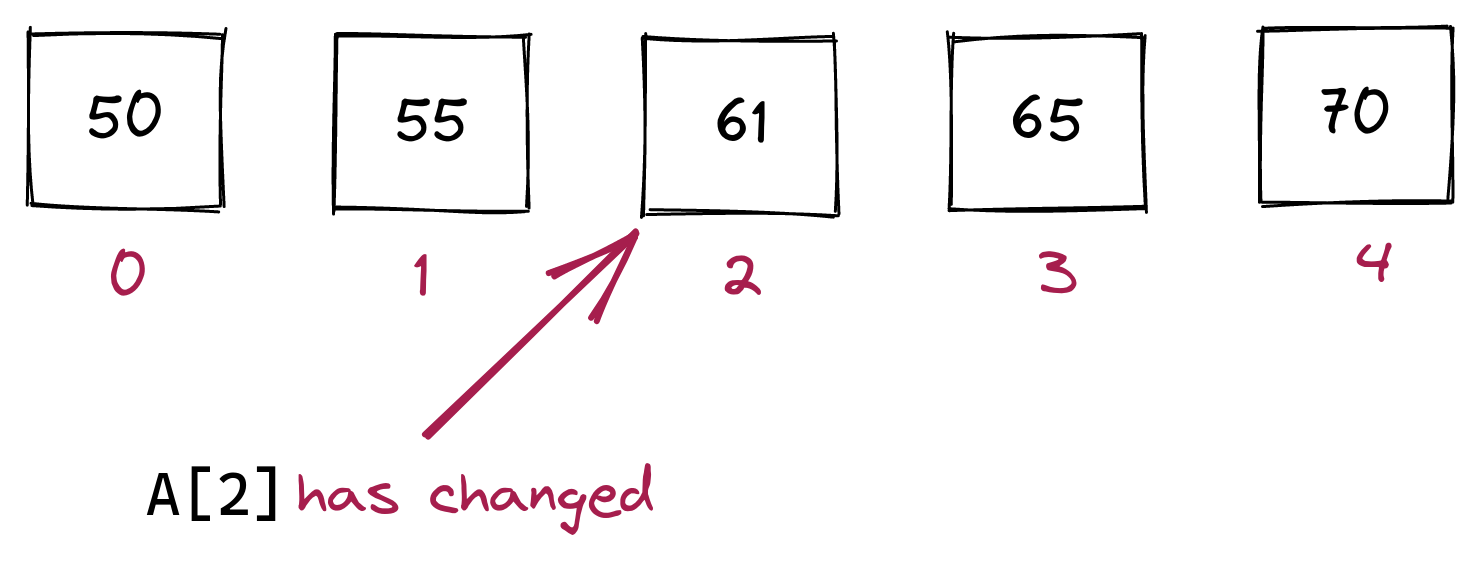
We can also change an element in an array:

A[2] = 61

which will result in the visualization:

the visualization

To explain how a 2D array works, let’s start with its conceptual visualization, via an example:

Consider this visualization of a 2D array:

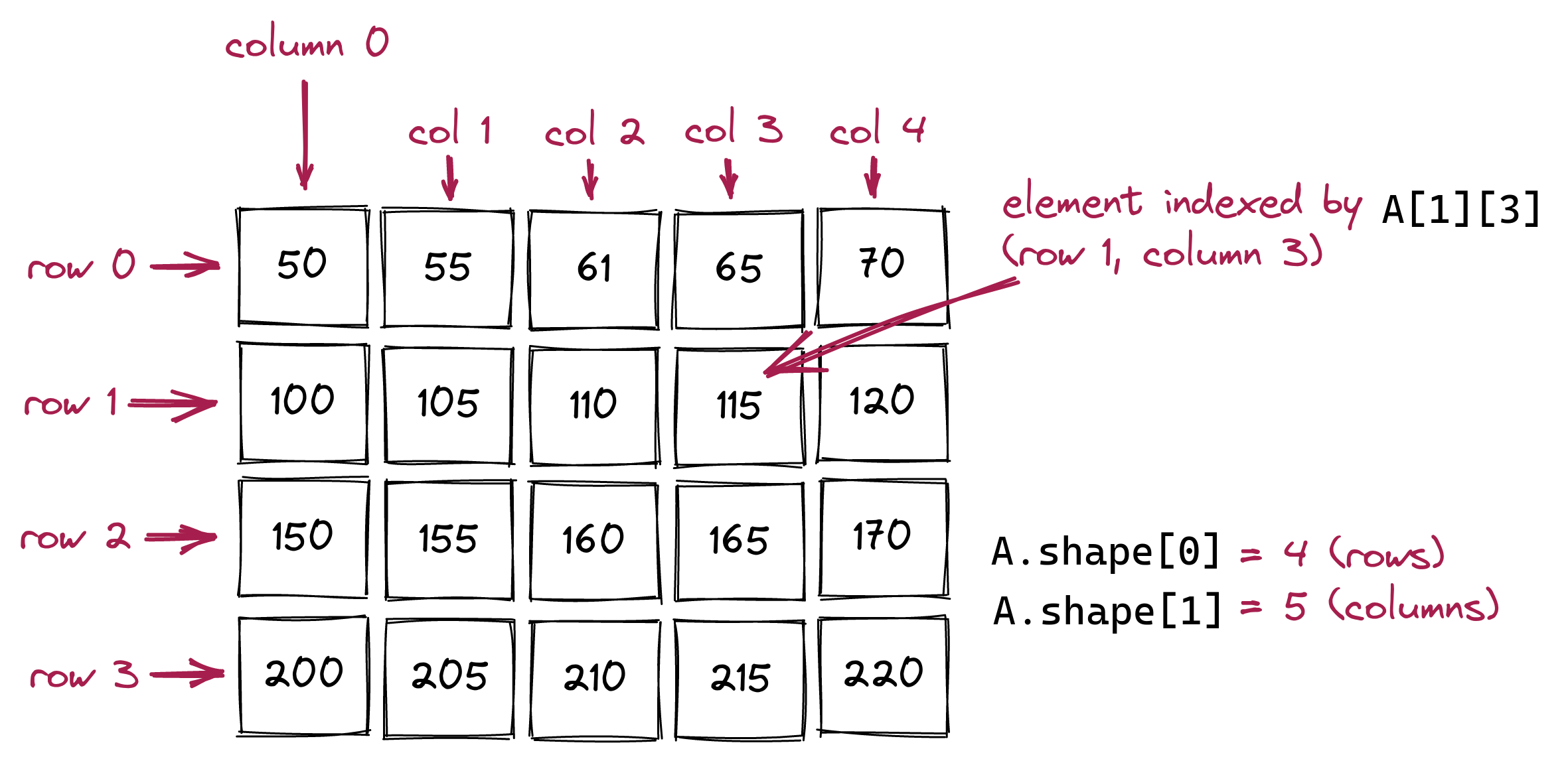
2D array

We use the term row to describe the contents going across one of the series of boxes going left to right:

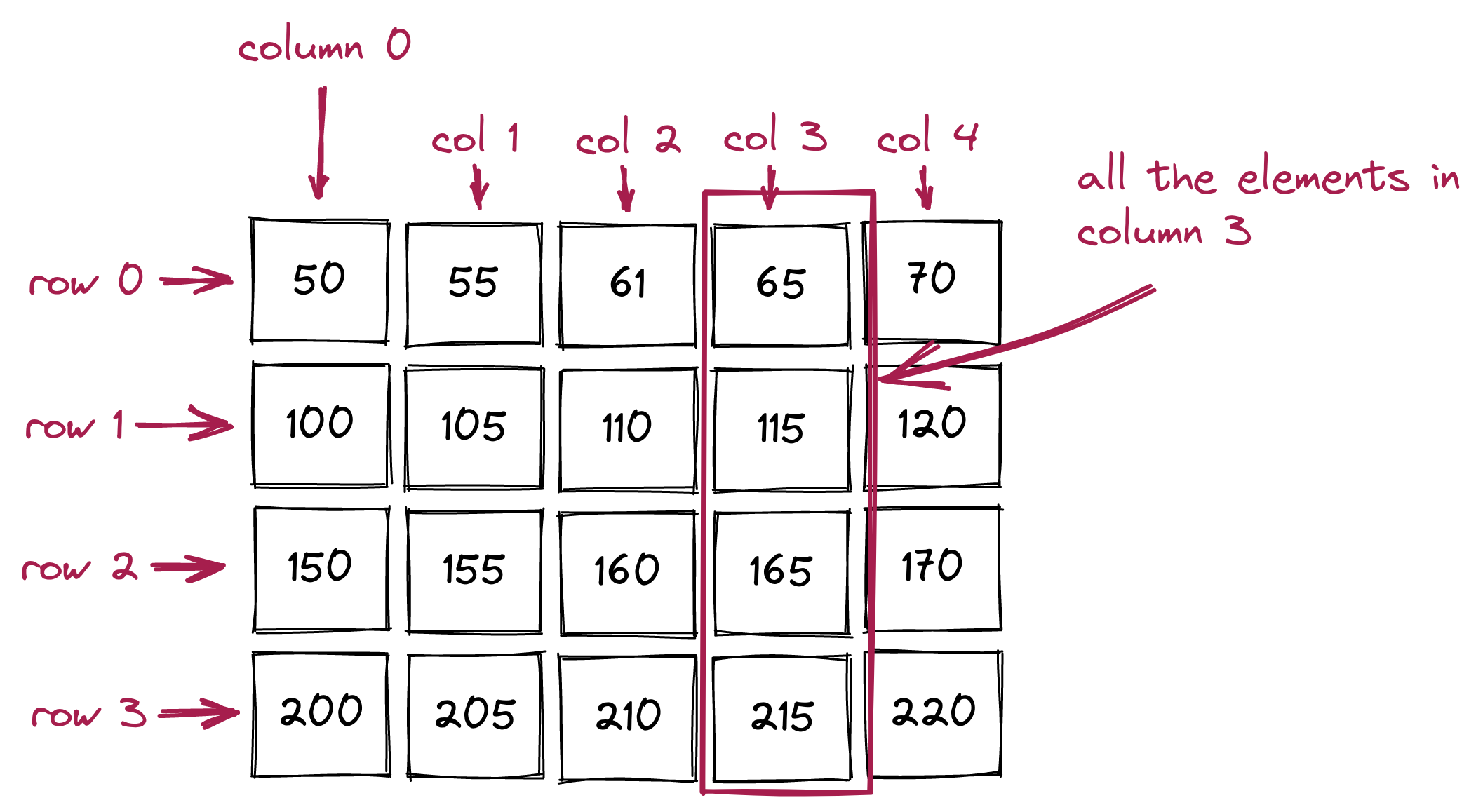
series of boxes

And the term column (shortened to col in our pictures) to describe the series of boxes going vertically top to bottom:

The number of elements in a row is the number of columns.
The number of elements in a column is the number of rows. Again, because our limited keyboard doesn’t let us draw boxes, we need a way to type in a 2D array. We do so by writing out a 2D array as a series of comma-separated rows:

A = np.array([ [50,   55,  60,  65,  70],
               [100, 105, 110, 120, 125],
               [150, 155, 160, 165, 170],
               [200, 205, 210, 215, 220] ])

Here, we’ve added whitespace (that’s allowed) to line up the rows so that it’s visually organized. To access a particular element, we need the row number and column number, as in:

print(A[1,3])     # NOT A[1][3]

Important: Unlike a list-of-lists, arrays can use comma separation. For comparison:

# List of lists:
X = [ [2,4,6,8,10], [1,3,5,7,9] ]
print(X[0][2])

# 2D array:
X = np.array([ [2,4,6,8,10], [1,3,5,7,9] ])
print(X[0,2])

Arrays allow box separation as well (like lists) but this causes problems in other array operations (slicing): so please use comma-separation with a single set of square brackets for arrays.

Just as we used a for loop for a single array, it is very typical to use a nested for loop for a 2D array:

For comparison, let’s look at a 1D array:

A = np.array( [1, 4, 9, 16] )
for i in range(A.shape[0]):        # Recall: A.shape[0] is the size
    print(A[i])

The equivalent for a 2D array is:

A = np.array([ [50,   55,  60,  65,  70],
               [100, 105, 110, 120, 125],
               [150, 155, 160, 165, 170],
               [200, 205, 210, 215, 220] ])

for i in range(A.shape[0]):        # number of rows
    for j in range(A.shape[1]):    # number of columns
        print(A[i,j])

To make the code a bit more readable, we could write

num_rows = A.shape[0]
num_cols = A.shape[1]
for i in range(num_rows):
    for j in range(num_cols):
        print(A[i,j])

Exercise 2.0.7

Consider this conceptual 2D array: In 2D_array.py, write code to create the array, and then a nested loop to print the array so that the output has one row on each line, with two spaces between elements, as in:

Exercise 2.0.8

In 2D_array2.py, use the same array above and structure a nested loop to compute the sum of elements down each column so that the output is:

Column 0 total is 14
Column 1 total is 23
Column 2 total is 25

About 2D arrays:

Although our examples show arrays of integers, the NumPy package supports a wide variety of data types, including floats, chars, and strings. There are even specially “compacted” versions of integers to enable working with extremely large arrays.
Two common (and quite different) uses of 2D arrays:
- One is for a mathematical construct called a matrix, which you is discussed in a linear algebra course.
- The other is for images, which we’ll look at next.

2.0.3 Greyscale Images as 2D Arrays

Consider the following program:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

greypixels = np.array([ [50,   55,  60,  65,  70],
                        [100, 105, 110, 120, 125],
                        [150, 155, 160, 165, 170],
                        [200, 205, 210, 215, 220] ])
dt.set_axes_off()
dt.draw_greyimage(greypixels)

dt.display()

Exercise 2.0.9

Type up the above in image_example.py and download drawtool.py into the same folder. Run the program and examine the image output as compared to the input array greypixels.

What is a greyscale image? By greyscale, we mean an image without colors, but rather shades of grey (often 256 shades). Consider this illustration showing an image on the left with a small part of it zoomed in:

zoomed in

Any digital image is really a 2D arrangement of small squares called pixels, in rows and columns (just like an array). In a greyscale image, each pixel is colored a shade of grey. In standard (“8-bit”) greyscale images, there are 256 shades of grey numbered 0 through 255, where 0 represents black and 255 represents white.

Now let’s go back to the code and examine what we wrote:

greypixels = np.array([ [50,   55,  60,  65,  70],
                        [100, 105, 110, 120, 125],
                        [150, 155, 160, 165, 170],
                        [200, 205, 210, 215, 220] ])

The first number (50) is a shade of dark grey (almost black).
The next number (55) along that row specifies a slightly lighter (but still quite dark) shade of grey.
Now consider 200, the first number in the 4th row: this is a shade of light grey, while 220 at the end is nearly white.
A greyscale image is nothing but a 2D array of integers whose values range between 0 and 255 (inclusive). Our eyes are fooled into seeing a seamless image because of high resolution.
Our eyes can see the individual pixels in the example above, a regular image has thousands or millions pixels, which is enough to fool the eye. -In a color image, as we will later see, we’ll need three numbers for each pixel (the amounts of red, green, blue). About the greyscale machine pictured above:
- This is an image of the ACE computer, one of the world’s earliest computers, designed by none other than Alan Turing, computer science pioneer and WWII hero.
- To give you a sense of how primitive these were, your laptop with 8GB RAM has more than 60 million times the memory of the ACE.
- And yet, the ACE was a landmark technological wonder at its time.

Let’s now work with an actual image:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

greypixels = dt.read_greyimagefile('eniac.jpg')
# greypixels is a 2D array

dt.set_axes_off()
dt.draw_greyimage(greypixels)

dt.display()

# Add code to print the number of rows, number of columns
# Should print: rows = 189  columns = 267

Exercise 2.0.10

Type up the above in image_example3.py and download eniac.jpg. Add code to print the number of rows and number of columns.

Image formats:

When an image is stored as a file, the file needs to contain all the integers that comprise the 2D array (for greyscale images)> Large images can take quite a bit of space.
For example, a 1000-row x 1000-column image will have one million pixels.
Many images have vast expanses of the same color or intensity and they offer a chance to compress (use less space by being clever).
Image formats arose as a result of wanting to both compress the storage and to store meta-info about images.
Popular formats include: JPG, PNG, GIF and Bitmap.
Typically the last part of the filename (the .jpg in eniac.jpg) tells you the format.
Python provides a way of reading from these formats so that we don’t have to worry about the details.

Let’s now modify a greyscale image:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

greypixels = dt.read_greyimagefile('eniac.jpg')

greypixels2 = np.copy(greypixels)
num_rows = greypixels2.shape[0]
num_cols = greypixels2.shape[1]

lightness_factor = 10

for i in range(num_rows):
    for j in range(num_cols):
        value = greypixels[i,j] + lightness_factor
        if value > 255:
            value = 255
        greypixels2[i,j] = value

dt.set_axes_off()
dt.draw_greyimage(greypixels2)

# To save an image, use the save_greyimage() function:
# dt.save_greyimage(greypixels2,'eniac-light.jpg')

dt.display()

Exercise 2.0.11

Type up the above in image_example4.py and try different values (in the range 10 to 100) of the lightness_factor. There is more than one “correct” answer!

Exercise 2.0.12

In image_example5.py write code to create the “negative” of a greyscale image (black turns to white, white to black, light grey to dark grey, dark grey to light grey, and so on). For example, applying this to the eniac.jpg image should result in eniac-negative.jpg.

2.0.4 Color Images as 3D Arrays

In a color image, each pixel will have a color instead of a “greyness” value.
Unfortunately, one cannot easily represent colors with a single number.
There are many ways of using multiple numbers to encode colors.
We’ll use the most popular one: specify the strengths of the three primary colors (Red, Green, Blue).
This approach is so popular that we refer to it simply as “RGB.””
The “amount” of red is a number between 0 and 255, the amount of green is another such number, as is the amount of blue.
Each color is therefore a group of three numbers, for example:
- (255,0,0) is all red (no green, no blue)
- (0,255,0) is all green (no red, no blue)
- (0,0,255) is all blue (no red, no green)
Let’s try a few more:
- (255,255,0)
- (100,255,255)
- (200,200,200) (grey is R,G,B all equal)
- (0,0,0)
- (255,255,255) is white

When each pixel needs three numbers and there’s a grid of pixels,how do we store the numbers?

We use a small array (of size 3) to store the triple. Then each pixel in the 2D array of pixels will have an array of size 3.
This is a 3D array!

Let’s look at an example:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

pixels = np.array(
    [ [ [255,0,0], [200,0,0], [150,0,0], [50,0,0] ], 
      [ [255,50,0], [200,100,0], [150,150,0], [50,200,0] ], 
      [ [255,50,50], [200,100,100], [150,150,150], [50,200,200] ], 
      [ [0,50,50], [0,100,100], [0,150,150], [0,200,200] ], 
      [ [0,0,50], [0,0,100], [0,0,150], [0,0,200] ]
  ]) 

dt.set_axes_off()
dt.draw_image(pixels)

dt.display()

Let’s point out the structure inherent in the above 3D array:

3d array

Next, let’s work with actual color images with an example application: converting color to greyscale.

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

# The image file is expected to be in the same folder
pixels = dt.read_imagefile('washdc.jpg')

num_rows = pixels.shape[0]
num_cols = pixels.shape[1]

greypixels = dt.make_greypixel_array(num_rows, num_cols)
for i in range(num_rows):
    for j in range(num_cols):
        # Average of red/green/blue
        avg_rgb = (pixels[i,j,0] + pixels[i,j,1] + pixels[i,j,2]) / 3
        # Convert to int
        value = int(avg_rgb)
        greypixels[i,j] = value

dt.set_axes_off()
dt.draw_greyimage(greypixels)

# Notice: saving to a different image format (PNG):
dt.save_greyimage(greypixels, 'washdc-grey.png')

dt.display()

Exercise 2.0.13

Type up the above in color_example3.py and download washdc.jpg. Compare the file size of the original versus the new greyscale file you created.

Next, consider the following program:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

pixels = dt.read_imagefile('washdc.jpg')

num_rows = pixels.shape[0]
num_cols = pixels.shape[1]

for i in range(num_rows):
    for j in range(num_cols):
        if ( (pixels[i,j,1] > pixels[i,j,0]) 
             and (pixels[i,j,2] < 0.5*pixels[i,j,1]) ):
            pixels[i,j,0] = 0
            pixels[i,j,1] = 0
            pixels[i,j,2] = 255

dt.set_axes_off()
dt.draw_image(pixels)

dt.display()

Exercise 2.0.14

Type up the above in color_example4.py. You already have washdc.jpg.

What did we just do?

We are examining the R,G,B values for each pixel, to see if the condition (G > R) and (B < G) is satisfied. When the condition is satisfied, we are overwriting the pixel with a new (all blue) color.
What we’re trying to do is identify greenery by asking: when do we have the Green value a bit larger than the Red value and much larger than the Blue value?
Why is this useful? This is essentially what many satellite-image applications do: identify areas of interest for urban planning, crop surveys, environmental assessment, and other uses.
Notice that this rule does not capture all greenery.

Exercise 2.0.15

In color_example5.py, try to add additional rules to capture the remaining greenery (the trees) and set those pixels to blue as well.

2.0.5 Arrays and Slicing

Slicing can be applied to arrays in the same way that we used them earlier for lists with one major difference, as we’ll point out. For example:

import numpy as np

print('list slicing')
A = [1, 4, 9, 16, 25, 36]
B = A[1:3]                 # B has [4, 9]
print(B)
B[0] = 5                   # B now has [5, 9]
print(B)
print(A)                   # What does this print?

print('array slicing')
A = np.array( [1, 4, 9, 16, 25, 36] )
B = A[1:3]                 # B "sees" [4, 9]
print(B)
B[0] = 5                   # What happens now?
print(B)
print(A)                   # What does this print?

Exercise 2.0.16

Type up the above in slicing_example.py. Did you get the results you expected?

The slicing expression 1:3 in A[1:3] refers to all the elements from position 1 (inclusive) to just before position 3 (so, not including position 3). With lists, a new list is created with these elements:

A = [1, 4, 9, 16, 25, 36]
B = A[1:3]

So, writing into the new list (B) does not affect the old list (A) from which the slice was taken. But with arrays, a slice is only a view as if we were giving a name to a zoomed-in-part:

A = np.array( [1, 4, 9, 16, 25, 36] )
B = A[1:3]

Here, array B refers to the segment (that’s still in A) from positions 2 to 3. This is why, if you make a change to B, you are actually changing A. Why did the authors of NumPy do this?

The reason is, many image processing applications require working on parts of images.
Then, with regular slicing, if we were to pull out parts and modify them, we’d have to write them back in.
Slicing makes it convenient to write directly into parts of images.

Slicing is a big sub-topic so we will point out a few useful things via an example:

# Color image:
A = np.array(
    [ [ [255,0,0], [200,0,0], [150,0,0], [50,0,0] ], 
      [ [255,50,0], [200,100,0], [150,150,0], [50,200,0] ], 
      [ [255,50,50], [200,100,100], [150,150,150], [50,200,200] ], 
      [ [0,50,50], [0,100,100], [0,150,150], [0,200,200] ], 
      [ [0,0,50], [0,0,100], [0,0,150], [0,0,200] ]
  ]) 

B = A[4:5,:,: ]   # The fifth row
print(B) 
C = A[:,1:2,:]    # The second column
print(C)
D = A[:3,:2,:]    # The pixels in the first three rows and first two columns
print(D)

A different slice can be specified for each dimension of a multidimensional array.
When neither end of a slicing range is specified, that implies all the elements, as in: B = A[4:5,:,:]
Here, the standalone colons imply the whole range for the 2nd and 3rd array index positions.
It is possible to specify just one limit as in: D = A[:3,:2,:]
In the first (row) case, we’re saying “all rows from the start up to row 2”.

Let’s apply slicing to creating a cropped image:

from drawtool import DrawTool
import numpy as np

dt = DrawTool()
dt.set_XY_range(0,10, 0,10)
dt.set_aspect('equal')

pixels = dt.read_imagefile('washdc.jpg')

# Crop from row 50 to 179, and column 50 to 199
pixels2 = pixels[50:180, 50:200]

dt.set_axes_off()
dt.draw_image(pixels2)

dt.display()

Exercise 2.0.17

In slicing_example2.py change the cropping so that the Washington Monument shows up centered in your cropped image, with little else around it.

2.0.6 Tuples

Suppose we want to write a function that computes both the square and cube of a number. One option is to write two separate functions:

def square(x):
    return x*x

def cube(x):
    return x*x*x

x = 5
print(x, square(x), cube(x))

We can alternatively write one function that computes and returns two things:

def square_cube(x):
    square = x*x
    cube = square*x 
    return (square, cube)

x = 5
(y, z) = square_cube(x)
print(x, y, z)

The return statement returns a pair of values: return (square, cube).
The pair is enclosed in parentheses.
And notice that, since two values are being returned, we need a pair to capture the return values: (y, z) = square_cube(x)

We can go beyond a pair to any number of such “grouped” variables:

def powers(x):
    square = x*x
    cube = square*x 
    fourth = cube*x
    fifth = fourth*x
    return (square, cube, fourth, fifth)  # returns four grouped variables

x = 5 
(a, b, c, d) = powers(x) # expects four grouped variables from the function
print(x, a, b, c, d)

Such a grouping of variables is called a tuple.

Tuples are similar to lists in many ways, but different in one crucial aspect: tuples are immutable.

First, let’s examine how to write the same square_cube() function above but using lists:

def square_cube_list(x):
    square = x*x
    cube = square*x 
    return [square, cube]

x = 5
[y, z] = square_cube_list(x)
print(x, y, z)

This works just fine. Another way in which a tuple is like a list is in using square-brackets and position indices to access individual elements, as in:

# List version:
L = square_cube_list(x)
print(L[0], L[1])      # L[0] has the square, L[1] has the cube

# Tuple version:
t = square_cube(x)
print(t[0], t[1])      # t[0] has the square, t[1] has the cube

However, here’s the difference:

# List version:
L = square_cube_list(x)
L[0] = 0              # This is allowed

# Tuple version:
t = square_cube(x)
t[0] = 0              # This is NOT allowed

Thus, you can replace a list element but you cannot replace a tuple element. This is in fact a bit subtle, as this example shows:

x = 3
y = 4
t = (x, y)   # The tuple's value is now fixed.
print(t)     # (3, 4)
x = 2
print(t)     # (3, 4)

Once the tuple is instantiated (that’s the technical term for “made”) then the tuple’s value cannot be changed. You can of course assign a different tuple value to a tuple variable as in:

t = (1, 2)
print(t)
t = (3, 4)
print(t)

Here, we’re simply replacing one fixed-value tuple with another. Hence, tuples are immutable (so are strings).

Why use tuples at all? It’s to allow programmers to signal clearly that their tuples shouldn’t be changed. This turns out to be convenient for mathematical tuples (like points on a graph), which are similar.

Groups of tuples can be combined into lists and other data structures. It’s very useful in working with points (the mathematical point you draw with coordinates) and other mathematical structures that need more than one number to describe.

For example, here’s a program that, given a list of points, finds the leftmost point (the one with the smallest x value).

def leftmost(L):
    leftmost_guess = L[0]
    for q in L:
        if q[0] < leftmost_guess[0]:
            leftmost_guess = q
    return leftmost_guess

list_of_points = [(3,4), (1,2), (3,2), (4,3), (5,6)]
(x,y) = leftmost(list_of_points)
print('leftmost:', (x,y) )

leftmost: (1, 2)

Exercise 2.0.18

Trace through several iterations of the above, then type in tuple_example.py to confirm the trace.

Exercise 2.0.19

Consider the following:

import math

def distance(p, q):
    return math.sqrt( (p[0]-q[0])**2 + (p[1]-q[1])**2 )

def find_closest_point(p, L):
    # Write your code here to find the closest point in L to p
    # and to return both the point and the distance to it from p.

list_of_points = [(3,4), (1,2), (3,2), (4,3), (5,6)]
query_point = (5,4)
(c, d) = find_closest_point(query_point, list_of_points)

print('closest:',c,' at distance', d)
# Should print: 
# closest: (4, 3) at distance 1.4142135623730951

In tuple_example2.py, fill in the missing code to find the closest point in a list of points to a given query point. Return both the closest point and the distance to the query point as a tuple.

2.0.7 Dictionaries

Consider this problem: We have a data file that looks like this:

apple
banana
apple
pear
banana
banana
apple
kiwi
orange
orange
orange
kiwi
orange

This might represent, for example, a record of sales at a fruit stand. We’d like to count how many of each fruit. One way would be to define a counter for each kind:

num_apples = 0
num_bananas = 0
num_pears = 0
num_kiwis = 0
num_oranges = 0
with open('fruits.txt','r') as data_file:
    line = data_file.readline()
    while line != '':
        fruit = line.strip()
        if fruit == 'apple':
            num_apples += 1
        elif fruit == 'banana':
            num_bananas += 1
        elif fruit == 'pear':
            num_pears += 1
        elif fruit == 'kiwi':
            num_kiwis += 1
        elif fruit == 'orange':
            num_oranges += 1
        else:
            print('unknown fruit:', fruit)
        line = data_file.readline()

print('# apples:', num_apples)
print('# bananas:', num_bananas)
print('# pears:', num_pears)
print('# kiwi:', num_kiwis)
print('# oranges:', num_oranges)

Exercise 2.0.20

Type up the above in fruits.py and use the data file fruits.txt to confirm. Next, in fruits2.py, change the program to accommodate the additional fruits in fruits2.txt.

Aside from being tedious, this approach has other issues:
- One would like to be able to write a general program that does not need to know which fruits are in a file. - What if there were a thousand different kinds of items? - A single mistake in a variable can cause the counts to be wrong.

Fortunately, the use of dictionaries will make it easy:

# Make an empty dictionary
counters = dict()

with open('fruits.txt','r') as data_file:
    line = data_file.readline()
    while line != '':
        fruit = line.strip()
        if fruit in counters.keys():
            # If we've seen the fruit before, increment.
            counters[fruit] += 1
        else:
            # If this is the first time, set the counter to 1
            counters[fruit] = 1
        line = data_file.readline()

print(counters)

Exercise 2.0.21

Type up the above in fruits3.py and first apply it to fruits.txt and then to fruits2.txt.

A dictionary is a technical term that is only somewhat related to an actual English dictionary. Think of an English dictionary as something where you look up a word and receive its meaning.
The operations here are look up and receive an associated value (the word’s meaning, in this case).
In Python, a dictionary is a structure that lets you associate one kind of data with another.
The technical equivalent of a word is called a key and the equivalent of the meaning is called the value.
So, a dictionary is a collection of key-value pairs. Here’s an example:

d = {'apple': 3, 'banana': 3, 'pear': 1, 'kiwi': 2, 'orange': 4}

In this case, we’re associating

The value 3 with the key ‘apple’
The value 3 with the key ‘banana’
The value 1 with the key ‘pear’
The value 2 with the key ‘kiwi’
The value 4 with the key ‘orange’ Conveniently, Python allows array indexing using the key:

d = {'apple': 3, 'banana': 3, 'pear': 1, 'kiwi': 2, 'orange': 4}

print(d['apple'])  # Prints 3

d['banana'] = 0    
# Which changes the value associated with 'banana' to 3

The above is an example of a dictionary that’s already built (after we’ve processed the data). To process data on-the-fly, we need an additional operation that an English dictionary does not really have: we need to be able to add something that’s not already there. To add a new key, we simply use it as an index:

d = {'apple': 3, 'banana': 3, 'pear': 1, 'kiwi': 2, 'orange': 4}

d['plum'] = 0

Important

A dictionary can only have one value for each key. Assigning a second value to a key overwrites the original value.

d = {'apple': 3}
print(d)
d['apple'] = 4
print(d)
e = {'peach': 2, 'peach': 5}
print(e)

{'apple': 3}
{'apple': 4}
{'peach': 5}

With this understanding we can now revisit the code in the fruit example.

# Make an empty dictionary
counters = dict()

with open('fruits.txt','r') as data_file:
    line = data_file.readline()
    while line != '':
        fruit = line.strip()
        if fruit in counters.keys():
            # If we've seen the fruit before, increment.
            counters[fruit] += 1
        else:
            # If this is the first time, set the counter to 1
            counters[fruit] = 1
        line = data_file.readline()

print(counters)

Lines 4, 5, 6 and 14 process the file line-by-line, as we’ve seen before
Line 8: if fruit in counters.keys(): checks to see if we have seen the fruit before by seeing if value of fruit is present as a key in the dictionary
- If the fruit has been seen before, counters[fruit] += 1 increments the count for that fruit by 1
- If it has not been seen (the else statement), counters[fruit] = 1 adds a new key to the dictionary for that fruit, with value equal to 1 (since it has been seen for the first time)

Exercise 2.0.22

In stopwords2.py, write code that uses a dictionary to compare the relative occurrence of stopwords in alice.txt and darwin.txt. These texts are Lewis Carroll’s Alice In Wonderland and Charles Darwin’s On the Origin of Species (the complete work for both cases). You will also need wordtool.py and wordsWithPOS.txt.

In particular, we’d like to know: what percentage of the stopword occurence can be attributed to ‘the’, what percentage to ‘and’, and so on.

Here’s some starter code:

import wordtool as wt 

# The 25 most common stopwords
stopwords = {'the': 0,'be': 0,'to': 0,'of': 0,'and': 0,'a': 0,'in': 0,'that': 0,
            'have': 0,'I': 0,'it': 0,'for': 0,'not': 0,'on': 0,'with': 0,'he': 0,
            'she': 0,'you': 0,'do': 0,'as': 0,'at': 0,'his': 0,'her': 0,'they': 0,
            'by': 0}

wt.open_file_byword('alice.txt')

s = wt.next_word()

'''
your code goes here
update the values of the dictionary based 
on the occurrences of the stopwords in the text
'''

for key in stopwords.keys():
  print('Stopword "' + key + '" is ' + str(stopwords[key]) + '% of stopwords')

For alice.txt the output should look like this (not necessarily in the same order) using the string formatting from the previous section.

Compare the outputs for the two texts: do the stopwords occur with similar relative frequencies across the two texts?

2.0.8 More Python Than You Require

Unit 2 will lightly sketch a few advanced topics to introduce ideas and show some examples, without expecting mastery of all the details.

You might ask: what’s left in Python to learn?

Quite a lot. - Like many modern programming languages, Python is large enough that one needs a few courses to experience all of it. - Some concepts are advanced enough to need weeks to cover (example: objects). - Others need a background in data structures to understand how they work (example: dictionaries). - Yet others involve library functions and external packages.

Do you need to learn more? Is what you’ve learned enough to put Python to work? We’ll have more to say about this shortly.

End-Of-Module Problems

Full credit is 100 pts. There is no extra credit.

Problem 2.0.1 (100 pts)

Write a function third_shortest that takes as input a string and returns the third-shortest word length. Words in the string will be separated by spaces. Do not include punctuation.

As an example, third_shortest('You should not judge, you should understand.') returns 6. (Note that by removing punctuation, judge is counted as length 5.)

Hint: Use The np.min function, the str.split function, and dicts.

Submit as third_shortest.py.

Problem 2.0.2 (100 pts)

Write a function binner that takes as input a list of numbers and:

Creates five equal size “bins” of numbers.
Counts how many numbers are in each bin
Returns a dict of those bins.

For instance, [1, 1, 1, 6] would have these five bins: 1-2, 2-3, 3-4, 4-5, 5-6. There are three numbers in the first bin, none in the second, third, and fourth, and one number in the last. (If a number falls exactly between two bins, it can go in either of these two, but not both.)

So: binner([1, 1, 1, 6]) would return: {'1.0-2.0': 3, '2.0-3.0': 0, '3.0-4.0': 0, '4.0-5.0': 0, '5.0-6.0': 1}.

You can call the keys for the bins whatever you like, as long as the values are correct.

Submit as binner.py.