Module 0.2 - Numbers

Objectives

By the end of this module, for simple “Hello World”-like programs, you will be able to:

Create variable declarations.
Assign values to variables by simple assignment, and print them out.
Distinguish between integers in strings versus actual integers.
Demonstrate ability to perform operations on integers for a desired output.
Simplify expressions with constants to single value.
Evaluate expressions with variables in them.
Convert English descriptions of operations into expressions.
Mentally trace execution with expressions and calculations.
Mentally trace expressions and calculations inside for loops.
Produce desired output using for loops and calculations.
Identify new syntactic elements related to the above. And, once we’ve worked with integers, we’ll also do some “number crunching”.

0.2.0 - An Analogy

Python uses variables, similar to variables in algebra, to store information. Consider the analogy of variables as storage boxes. Consider the following rules about these boxes:

Each box can store only one item.

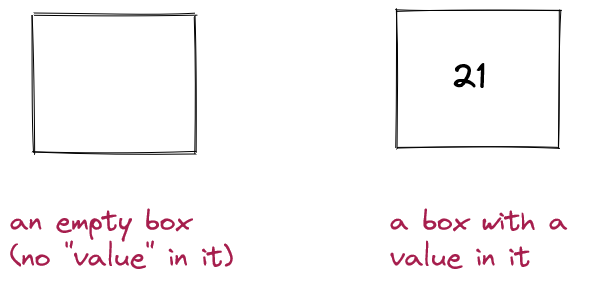
simple range

The possible things that can be stored inside are called values. Thus, at any given moment, a box’s value is whatever’s inside it.
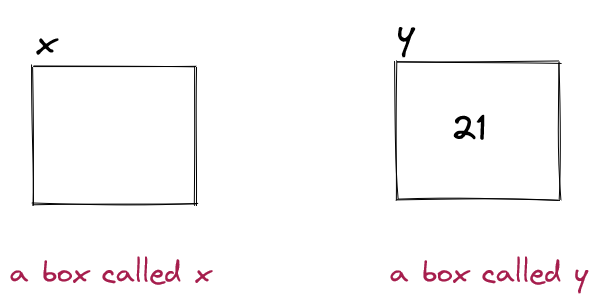
Each box has a unique name:

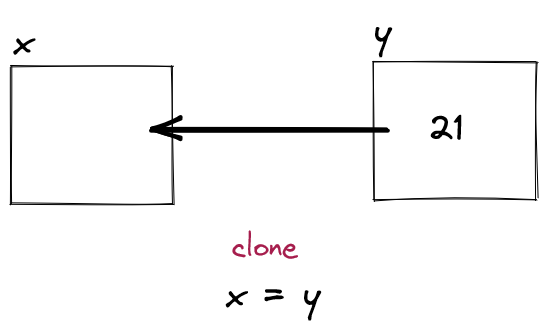
simple range

There is a cloning process that works like this:

simple range

The value inside one box is cloned.
The cloned value is placed inside another. There is a strange shortcut notation to specify cloning:

x = y

Here, the = (equals sign) does not mean “equals.”

It has been repurposed to mean “clone”, “copy,” or, in programming-language jargon, “assign”.
The value on the right side of the assignment operator is assigned to the variable on the left.
Important: Remember, a variable(box) can hold only one value at a time.

0.2.1 - Integer Variables

We’ll now start working with variables that hold integers (whole numbers like 3, 17, 2097, but not numbers like 3.141).

Consider this program:

i = 5
print(i)

Exercise 0.2.1

Type up the program in variable_example.py. What does it print?

Now let’s examine key parts of this program:

First, i is the name of a “box” (of sorts). The term used for “box” is variable . i is a variable. To put something in a variable, we use assignment with the repurposed = (equals) sign.

simple range

When we print a variable, what gets printed is its value. Thus, the number 5 gets printed

simple range

Important: What you see on printed out is the number 5 and NOT the letter i, thus when you see print(i) you should think: - “Hmmm, the print function is going to print the contents of variable i”. - “I wonder what’s inside i?” - “Let me look in the program to see what was the most recent value that got written into i”. For example:

i = 5
i = 3
print(i)

Exercise 0.2.2

Type up the above in variable_example2.py and confirm that 3 is what gets printed.

By way of explanation:

Exercise 0.2.3

Is it possible to not have a value in a variable? Consider this program:

i
print(i)

Type up the program in variable_example3.py You will see an error: fix the error (there is more than one way).

Thus: when you make a variable, you need to put something in it.

Next, let’s look at assignment between variables: This is the analogue of cloning between “boxes”. Consider this program:

i = 5
j = i     # The value in i gets copied into j
print(j)  # Prints 5

We say, in short, ” i is assigned to j“. Notice: we’ve used comments above to annotate and explain. We’ll do this often, knowing that comments are not executed.

Exercise 0.2.4

Consider this program:

i = 5
j = i
print(j)
print(i)   # Did i lose its value?

Type up the program in variable_example4.py

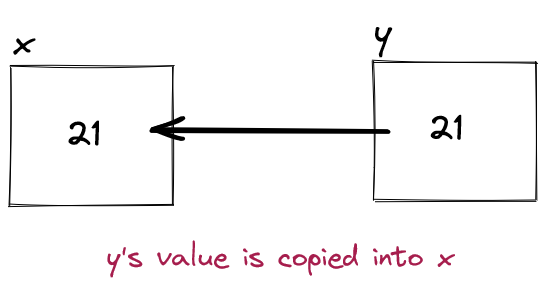
The above example illustrates that the value in i gets copied into the variable j, which means that the value 5 is still in the variable i.

Exercise 0.2.5

Consider this program:

i = 5
j = i
k = j
print(k)

Try to identify the output of this program just by mental execution. Type up the program in variable_example5.py and confirm.

Exercise 0.2.6

Consider this program:

i = 5
j = i
i = 0
k = j
j = 0
print(k)

Try to identify the output of this program just by mental execution. Type up the program in variable_example6.py and confirm.

Note that a copied value does not change if the original is changed. For example, consider:

i = 5
j = i      # j now has 5
i = 0      # We changed i here
print(j)   # j still has 5

Here’s the line-by-line execution: - The first line puts the value 5 in variable i. The second line copies the value ini(which is 5) into j. Sojwill have the value 5 as well. - The third line replaces the value 5 with value 0. -jstill has 5, so the fourth line will print 5. - Note: 0 is an actual value, and is not “no value” or “nothing”.

Exercise 0.2.7

Type up the following lines of code in variable_example7.py

i = 5
j = 6      

# Add code between here

# and here.

print(i)   # should print 6
print(j)   # should print 5

Add some lines of code with the objective of swapping the values in variablesiand j. You will need a third variable to be used as a holding place. Thus, without directly assigning the number 5 tojor the number 6 to i, write code using a third variable to achieve the desired swapping of values.

0.2.2 - Integer Operators

Let’s examine the familiar arithmetic operators +, -, *, /:

Addition: +
Subtraction: -
Multiplication: *
Division: /

Consider this example with addition:

i = 5
j = 6
k = i + j
print(k)

What happens during execution:

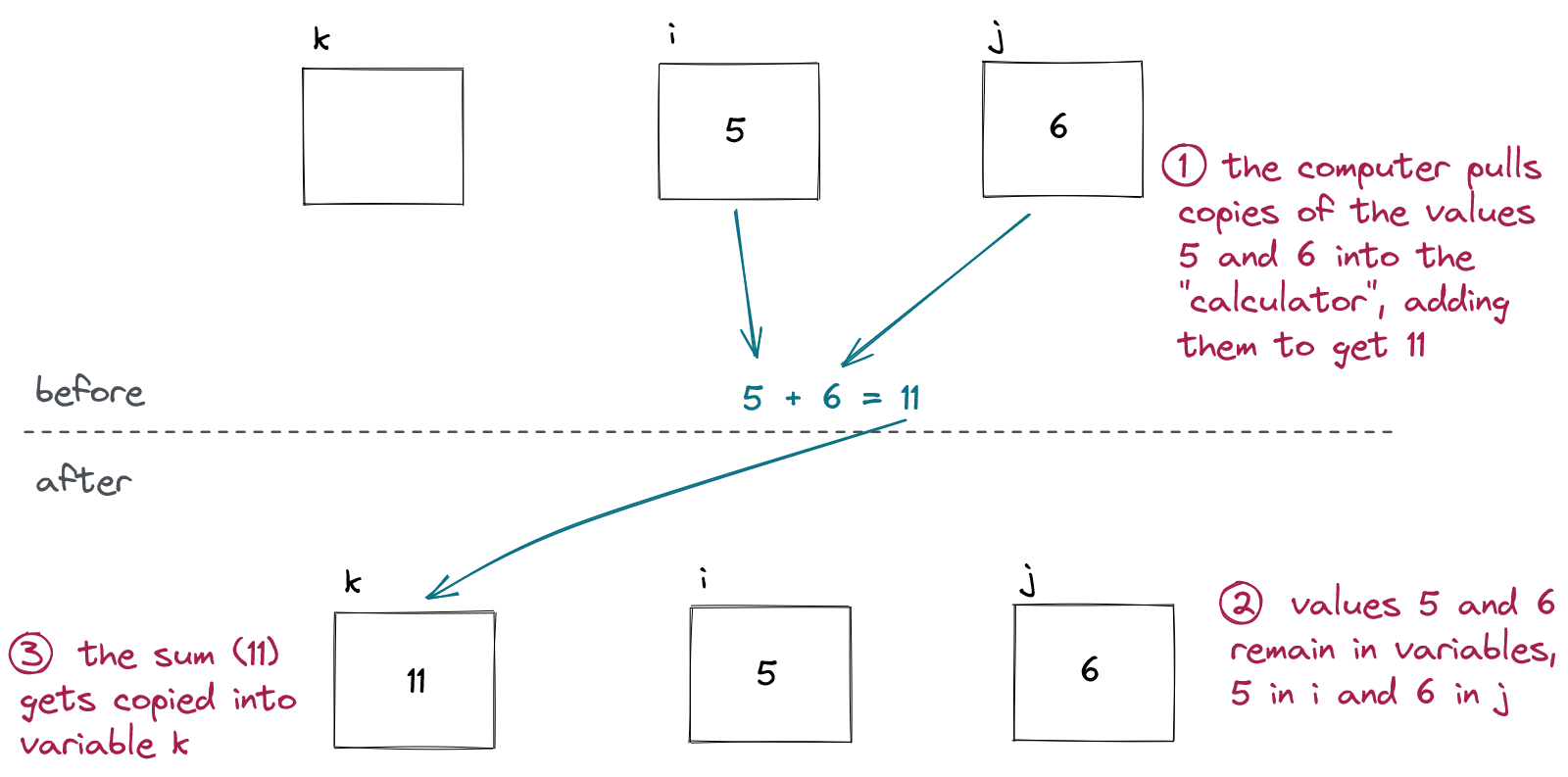
addition with variables

The values in i and j are added. The resulting value goes into variable k.
A long-ish way of saying this aloud:

“k is assigned the sum of the values of i and j”

A shorter way: - “k is assigned i plus j”

Here’s an example with multiplication and division:

i = 5
j = 6
k = i * j
print(k)      # prints 30
m = i / j
print(m)      # what does this print?
n = i // j
print(n)      # what does this print?

Exercise 0.2.8

Type up the above in variable_example8.py. Now, find values of i and j such that the printed output is

36
4.0
4

Save your program with these values of i and j.

Integer division: In math, we learned that 1/4 = 0.25 and 21/6 = 3.5. This remains true in Python when we do something like

i = 21
j = 6
m = i / j

On the other hand, if we wish to perform integer division, we can use the integer division operator:

i = 21
j = 6
m = i // j

That is, the result is truncated down to the nearest integer.

Example: 3 // 2 becomes 1 because 1.5 gets truncated to 1.
Example: 15 // 4 becomes 3 because 3.75 gets truncated to 3.
Integer division is useful when we want to do integer arithmetic.

0.2.3 - Expressions and Operator Precedence

Consider the following program:

i = 5
j = 6
k = i*j - (i+1)*(j-1)
print(k)

About expressions:

An expression combines constants (like 1 , above), and variables using operators. Example: i*j - (i+1)*(j-1).
The above expression is really equivalent to: (i*j) - ((i+1) * (j-1)). Here, we added some clarifying parentheses.
Operator precedence allows us to reduce the number of clarifying parentheses. Python precedence follows standard precedence in math: /, *, +, -.
You might remember the precedence via the acronyms BODMAS or PEMDAS. (Look it up.)
The above expression is NOT the same as: i*j - i+1*j-1.
Also, note the change of whitespace: We could have written k = i * j - (i + 1) * (j - 1). But k = i*j - (i+1)*(j-1). is easier to read.
Sometimes you might find it useful to add “unnecessary” parentheses to organize your expression for human readability.

Let’s dive a bit deeper into precedence and do some examples: - We’ll use the four operators: addition (+), subtraction (-), multiplication (*), and division (/). We’ll use small integer to illustrate. Note: The key to working them out is to use extra parentheses in the right way.

The PEMDAS rule: apply Parentheses, then Exponents, then Multiplication and Division, and then Addition and Subtraction.

Example: 3 + 2*4

Here, we apply 2*4 to get 8
Then do 3 + 8 to get 11.
Applying extra parenthesis, i.e. 3 + (2*4), can makes it more clear.

Example: 3*(24/3-2*3) First, work out what’s inside the parentheses (the P of PEMDAS):

Do division of 24/3 and multiplication of 2*3 to get (8 - 6)
This gives (2)
Now go out and see that we need to do `3*(2)``
Which gives 6.
Using extra parentheses and spacing makes it clear: 3 * ( (24/3) - (2*3) )

Example: 1 + ( (4 - 1) * 8) / 6

Do the innermost parentheses first: (4 -1) = 3
Which results in 1 + (3 * 8) / 6
Then the next parentheses to get: 1 + 24/6
Then the D in PEMDAS: 1 + 4
Result: 5

Exercise 0.2.9

What does the expression \(i \cdot j - i + 1 \cdot j-1\) evaluate to when i=7 and j=3? Write a program example_expression.py to compute the value - your program should print the value after calculating it.

0.2.4 - More About Expressions and Assignment

The remainder operator: The expression 10 % 3 is “the remainder when 10 is divided by 3”. Thus 10 % 3 yields 1.

Similarly 11 % 4 is 3. The remainder operator is sometimes called modulo, as in “ten modulo 3 is 1”

Consider this example:

i = 14
j = -6
k = i % (-j)
print(k)

Exercise 0.2.10

Can you mentally execute and identify what’s printed in the code above? Type up the above in expression_example2.py to confirm.

One way to know whether one number cleanly divides another is to apply the % (remainder) operator.

print(10 % 2)
print(11 % 2)
print(12 % 5)
print(12 % 3)

Try running the above code. You can see that for numbers that divide evenly (10 and 2, 12 and 3), the result is 0.

0.2.5 - Shortcut Operators

Because it is common to add values into (and subtract values out of) existing variables, Python has built-in shortcut operators for these operations.

Consider this program, which

x = 5
print(x)
x = x + 1
print(x)

We can write this using the “shortcut addition” operator += as follows:

x = 5
print(x)
x += 1
print(x)

s += i is the same as s = s + i One can read s += i as “add i to what’s already in s, and store the result in s”.

This can be applied to the other operators as well:

s -= i         # Same as s = s - i
p *= 2         # Same as p = p * 2
d /= 2         # Same as d = d / 2

0.2.6 - Floating Points

So far all of the numeric variables we have worked with have been integers, whole numbers without decimals. However, it is often useful to work with decimals and fractions.

Because of computers store information, integers and decimal values are handled slightly differently.
Decimals are formally called “floating point” numbers (because of how the decimal point is stored).
Floating point numbers are often called “floats,” for short.

Python automatically returns a float from a mathematical operation when it is appropriate:

x = 6 / 3
print(x)
y = 5 / 3
print(y)
z = 1 + 2.5
print(z)

2.0
1.6666666666666667
3.5

Exercise 0.2.11

Write up the above as float_behavior.py. Add a multiplication operation that results in a float.

From the addition example, you can see that Python automatically takes an operation between an integer and a float and returns a float.
Sometimes two operations between integers result in a float, such as divsion.

An operation between two floats that yields a whole number still results in a float:

x = 1.5 + 1.5
print(x)

3.0

The distinction here is that the value displayed as 3.0 is a float, whereas something displayed as 3 would be an integer.

Floating Point Precision

Because of how computers represent numbers, floating point variables are not always perfectly precise.

For instance, we know that \(1 + 2 = 3\). Python’s integer math represents this correctly:

x = 1 + 2
print(x)

We also know that \(0.1 + 0.2 = 0.3\). However, this is a case where Python is slightly imprecise!

x = 0.1 + 0.2
print(x)

0.30000000000000004

Understanding and predicting the exact nature of these errors (“floating point errors”) is a complicated topic: for now, you should simply know that these errors exist.

0.2.6 - Converting Ints and Floats

Python has built in functions int() and float() to convert between these two types of numeric variables.

int() will truncate the floating point number at the decimal point.
float() converts exactly.

x = float(5)
print(x)
y = int(2.6)
print(y)

5.0
2

0.2.8 - When Things Go Wrong

As you might imagine, there are many ways to inadvertently create errors. In each case below, first try to identify the error just by reading. Then, type up the program to confirm.

Exercise 0.2.12

What is the error in this program?

i = j
j = 4
print(i)

Type it up in error1.py to confirm.

Exercise 0.2.13

What is the error in this program?

i = 4
j = 3
k = ( (i + j) * (i - j) / 2
print(k)

Type it up in error2.py to confirm.

We’ll now see a different kind of error:

n = 2
print(4/n)
n -= 2
print(4/n)

Exercise 0.2.14

Type it up in error3.py and see. “Fix” the error - modify the code so that the error does not occur.

The above is an example of a runtime error : The code itself is correctly written in that there are no issues with breaking the rules of the language. However, wheni is 0, you can’t divide by 0.

This causes a runtime error, meaning the program runs fine until the particular occurrence of divide-by-zero.

0.2.9 - Big Picture

Another in our series of occasional “big picture” sections that will step back from the material to comment on how we can learn better.

This was a long module with lots of exercises and details. Let’s review:

We introduced the all-important concept of a variable along with the sense that there’s a “place” in the computer for each variable.
- The “place” is really in the memory (also called RAM) of the computer.
Along with variables is the notion of assignment , which means “copying the value in one variable into another variable”. Note: assignments are amongst the most common of statements in everyday code.
When a variable is of a numeric type like integers, we also need to go over basic operators and show examples.
We learned that Python handles numbers with decimals (“floating point numbers”) slightly differently than it handles integers.

If you have to go back to some of the material to review or try some exercises again, that’s fine. You’re going to get better at this!

End-Of-Module Problems

Full credit is 100 pts (complete at least three problems). There is no extra credit.

Problem 0.2.1 (40 pts)

Modify line 3 of following program such that j is added to x instead of 2.

x = 5
j = 4
x = x + 2 # modify only this line
print(x)

The result should print 9. Submit as simple_addition.py.

Problem 0.2.2 (40 pts)

Add code to line 4 of following program to add i, j, and k, divide the result by two, and assign the result to variable x, i.e.:

\(x = \frac{i + j + k}{2}\)

i = 3
j = 4
k = 5
# add your code here
print(x)

The result will be a floating point number, 6.0. Submit as simple_math.py.

Problem 0.2.3 (40 pts)

Add code to line 4 of following program to add x and twice y divide the result by 3, convert the result to an integer and assign the result to variable z, i.e.:

\(x = \frac{x + 2 \times y}{3}\) converted to an integer.

x = 7
y = 4
# add your code here
print(z)

The result will initially be a floating point number, 5.0, which after conversion to an integer will be 5, resulting in this printed output:

Submit as more_math.py

Problem 0.2.4 (40 pts)

The following program intends to implement the following mathematical operation:

\(w = \frac{x + 3 \times y}{z - 2}\).

x = 7
y = 4
z = 3
w = (x + 3 x y/(3 - z))
print(w)

The program contains several errors. Fix them.

The result will be a floating point number, 19.0. Submit as math_errors.py.