Module 1.3 - Booleans, Strings, Built-ins, and Types

Objectives

By the end of this module you will be able to:

Practice working with Boolean expressions and variables.
Practice examples with strings
Start to use built-in functions
Delve into the notion of type

1.3.0 Boolean variables: Two Examples

Recall: An integer variable takes on values like 5 and -33:

x = 5
y = -33

A floating-point variable stores real numbers like:

x = 5.0014
y = -33.3333334

A string variable stores strings or chars, as in:

s = 'hello'
c = 'z'

A boolean variable stores one of two values: True or False
For example:

a = True
print(a)

b = False
print(b)

c = not a
print(c)

d = a or b
print(d)

e = a and b
print(e)

Exercise 1.3.1

Type up the above in boolean_example.py and run to examine the output.

The reserved words True and False are used in their usual sense. A boolean variable can store only one of these values:

a = True
b = False

Notice: True and False start with capitals. These aren’t the same as the quote-delimited strings 'True' and 'False'
Just as we could perform arithmetic on integer variables, so can we perform boolean operations on boolean variables. The simplest one is not:

a = True
c = not a

Since a has the value True then not a will have the value False
Thus, c will have the value False.

Likewise:

a = False
c = not a
print(c)

will print True.

Shown in table form, not is simple:

The `not` Operator
`a`	`not a`
`True`	`False`
`False`	`True`

Next, consider or:

d = a or b

How or works:

a or b will be True when one or more of them is True.
Another way to state it: a or b will be False only when a and b are both False.

This table shows all the combinations:

The `or` Operator
`a`	`b`	`a or b`
`True`	`True`	`True`
`True`	`False`	`True`
`False`	`True`	`True`
`False`	`False`	`False`

Next, consider and

e = a and b

How and works: a and b will be True only when both are True.

The `and` Operator
`a`	`b`	`a and b`
`True`	`True`	`True`
`True`	`False`	`False`
`False`	`True`	`False`
`False`	`False`	`False`

Let’s look at another example:

a = True
b = True

a = not a       
x = a and b
y = a or b
print(x, y)

Exercise 1.3.2

Type up the above in boolean_example2.py.

Look at:

a = True
b = True

Here, there are two boolean variables, each of which is assigned a (boolean) value. Think of the variables as “boxes” in the usual way but as boxes that can hold only boolean values (True or False).

Next, look at

a = not a

Here, the value in a before this executes is True So, not a is False . This gets stored in a So, after the statement executes a will have the value False . Next, look at

x = a and b

We know that a has the value False in it, while b has the value True . Thus, the and operator is applied to the values False and True. You can picture this as: False and True.
What is the result? Similar to applying the “rules of multiplication” to two numbers, we apply the rules of and to False and True.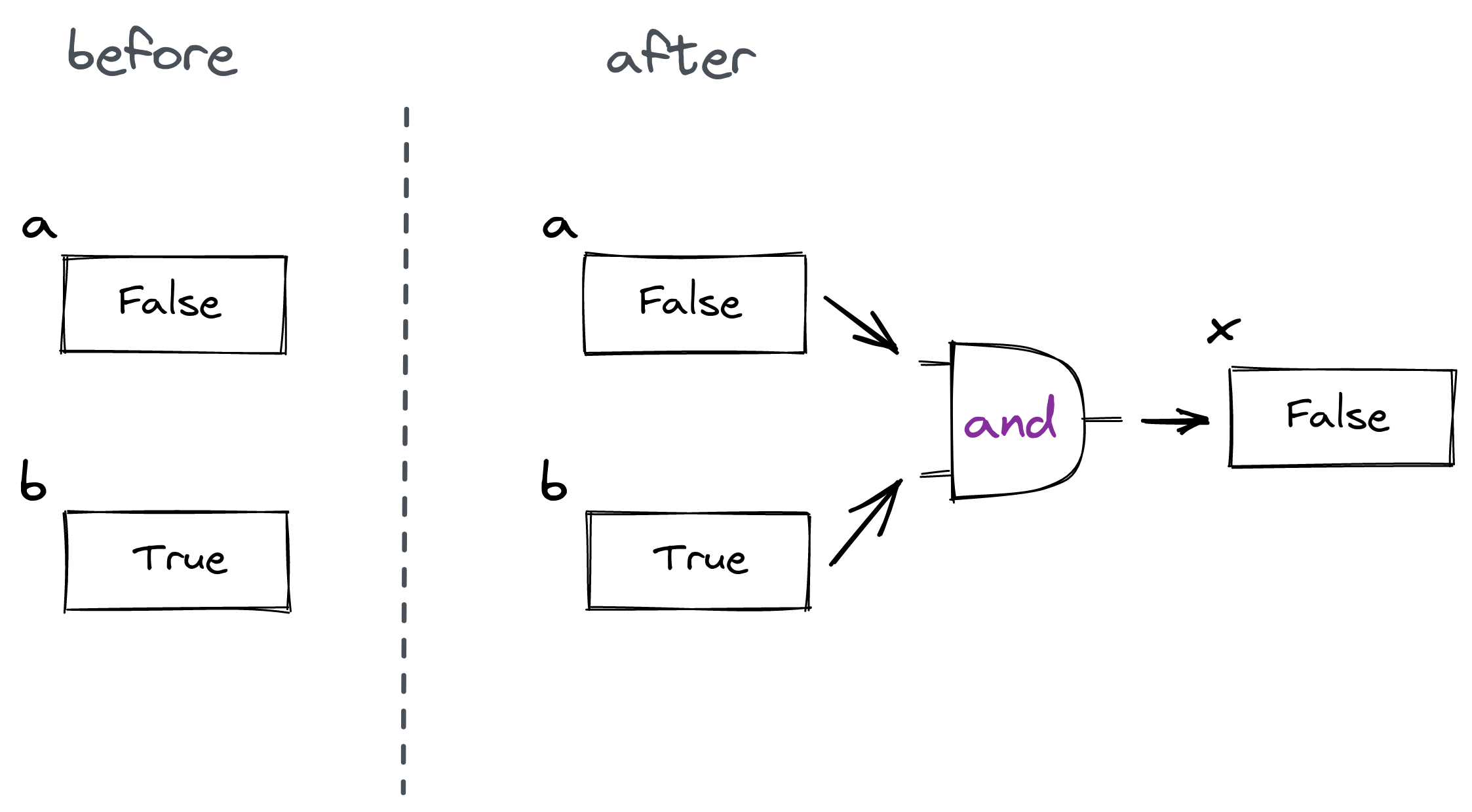

and diagram

The result is: False . Thus, the value False is assigned to the variable x.

The next statement is:

y = a or b

Because a is now False and b is True, the result in y will be:

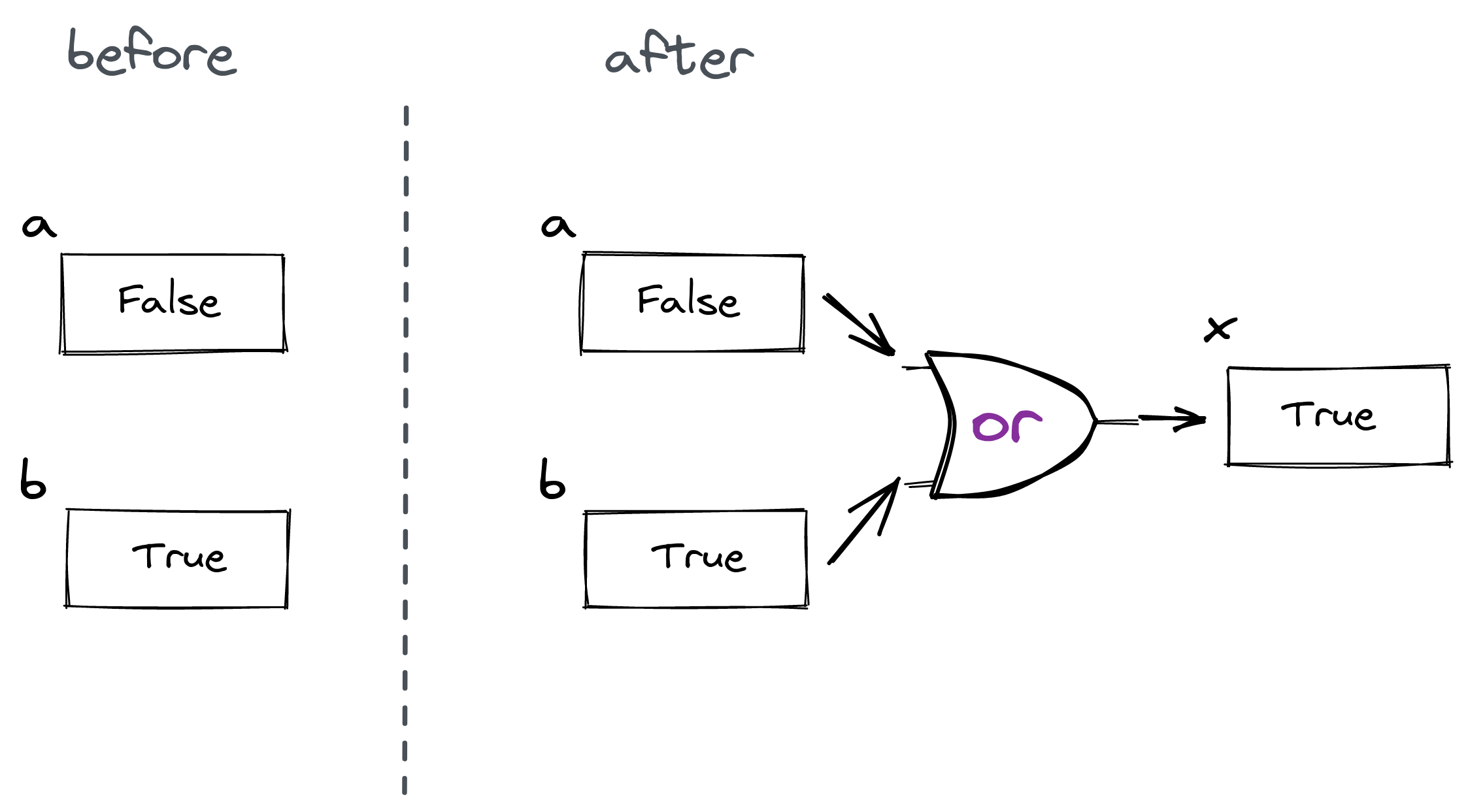
or diagram

1.3.1 Combining Boolean Operators

Consider

a = True
b = False
c = True
u = (a and b) or (a or b)
v = (not u) or (not (b and c))
print(u, v)

Let’s draw an expression diagram to help us understand what happens with the first expression:

or diagram

Exercise 1.3.3

Draw an expression diagram to work out the result for the second expression (the value of v) above. Then type up the above in boolean_example3.py to confirm.

Boolean expressions can be constructed with numeric variables and their comparison operators:

k = 5
m = 3
n = 8
a = True
b = False

first = (m < k) and (n > k)
second = ( (k+m == n) or (k-m < 10) )
third = first and (not second)
fourth = first or a
print(first, second, third, fourth)

Note: Since m is 3, k is 5, the expression (m < k) in

first = (m < k) and (n > k)

evaluates to True.

Similarly, the expression (n > k) also evaluates to True since n = 8 in

first = (m < k) and (n > k)

Thus, the resulting expression on the right side becomes:

first = True and True

Which evaluates to True from the rules (the table) for and.

Exercise 1.3.4

Draw an expression diagram to work out the result for the remaining three expressions above. Then type up the above program in boolean_example4.py to confirm.

1.3.2 Using a Boolean Variable

To see how a Boolean variable is used in practice, we will work through a somewhat elaborate example that will teach us other useful things.

Let’s start with this program:

def print_search_result(A, search_term):
    if search_term in A:
        print('Found ', search_term)

B = [15, 3, 23, 9, 14, 4, 6, 2]
print_search_result(B, 4)

Here, the goal is to create a function that takes a list, and a search value (or search term) and looks inside the list to see if it exists. Does the program work?

Exercise 1.3.5

Type up the above program in search_example.py to confirm.

Note: We have exploited the in operator in Python to examine whether or an element exists in a list: if search_term in A:

This will return either True or False. Python does the work of traversing the list and peeking inside to see if value (4 in this case) is in the list.

Now consider the problem of also printing the position where it’s found:

def print_search_result(A, search_term):
    for k in range(len(A)):
        if A[k] == search_term:
            print('Found', search_term, 'at position', k)

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 4)

Does this work?

Exercise 1.3.6

Type up the above program in search_example2.py to confirm.

Note: We are now traversing the list ourselves:

for k in range(len(A)):

Here, k will start at 0 and go up to the last index (one less than the length of the list). At each iteration, we check to see if the search term is equal to the list element at the current position (determined by k):

if A[k] == search_term:

If so, we’ve found it.

Exercise 1.3.7

Use the list

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 4)

and trace through the above program. Also trace through what happens when we instead have

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 5)

(There is nothing to turn in for this exercise.)

What we’d like to do is print something when a search term is not found in the list.
Consider this program:

def print_search_result(A, search_term):
    for k in range(len(A)):
        if A[k] == search_term:
            print('Found', search_term, 'at position', k)
    print('Not found:', search_term)

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 4)
print_search_result(B, 5)

Exercise 1.3.8

Start by thinking through the execution to see if this worked. Then, type it up in search_example3.py to see.

Let’s try another variation:

def print_search_result(A, search_term):
    for k in range(len(A)):
        if A[k] == search_term:
            print('Found', search_term, 'at position', k)
        else:
            print('Not found:', search_term)

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 4)
print_search_result(B, 5)

Exercise 1.3.9

Start by thinking through the execution to see if this worked. Then, type it up in search_example4.py to see.

We’ll now see how a simple Boolean variable is commonly used in these types of problems:

def print_search_result(A, search_term):
    found = False
    pos = -1
    for k in range(len(A)):
        if A[k] == search_term:
            found = True
            pos = k

    if found:
        print('Found', search_term, 'at position', pos)
    else:
        print('Not found:', search_term)

B = [15, 4, 23, 9, 4, 6]
print_search_result(B, 4)
print_search_result(B, 5)

Trace through the above.

Exercise 1.3.10

Type up the above program in search_example5.py and confirm the trace.

1.3.3 Returning a True/False value

Possible the most commonly use of Booleans is to write a function that returns True or False.

Suppose we want to determine whether or not a list has a negative number:

def has_negative(A):
    for k in A:
        if k < 0:
            return True
    return False

B = [2, 4, -10]
print(has_negative(B))
C = [1, 3, 5]
print(has_negative(C))

Trace through the above program.

Exercise 1.3.11

Type up the above program search_negative.py to confirm the trace.

Exercise 1.3.12

In search_negative2.py complete the function below to identify whether or not a list has exactly two negative numbers:

def has_two_negatives(A):
    # Write your code here

B = [2, 4, -10]
print(has_two_negatives(B))  # Should print False
C = [1, -3, -5]
print(has_two_negatives(C))  # Should print True
D = [1, -3, -5, -7]
print(has_two_negatives(D))  # Should print False

1.3.4 Strings and Slicing

It is common to want to pull out parts of strings.

For example, if the user in some application types ‘DC 20052’, we may want just the zip code:

s = 'DC 20052'
state = s[0:2]
zipcode = s[3:8]
print(state, zipcode)

Let’s explain:

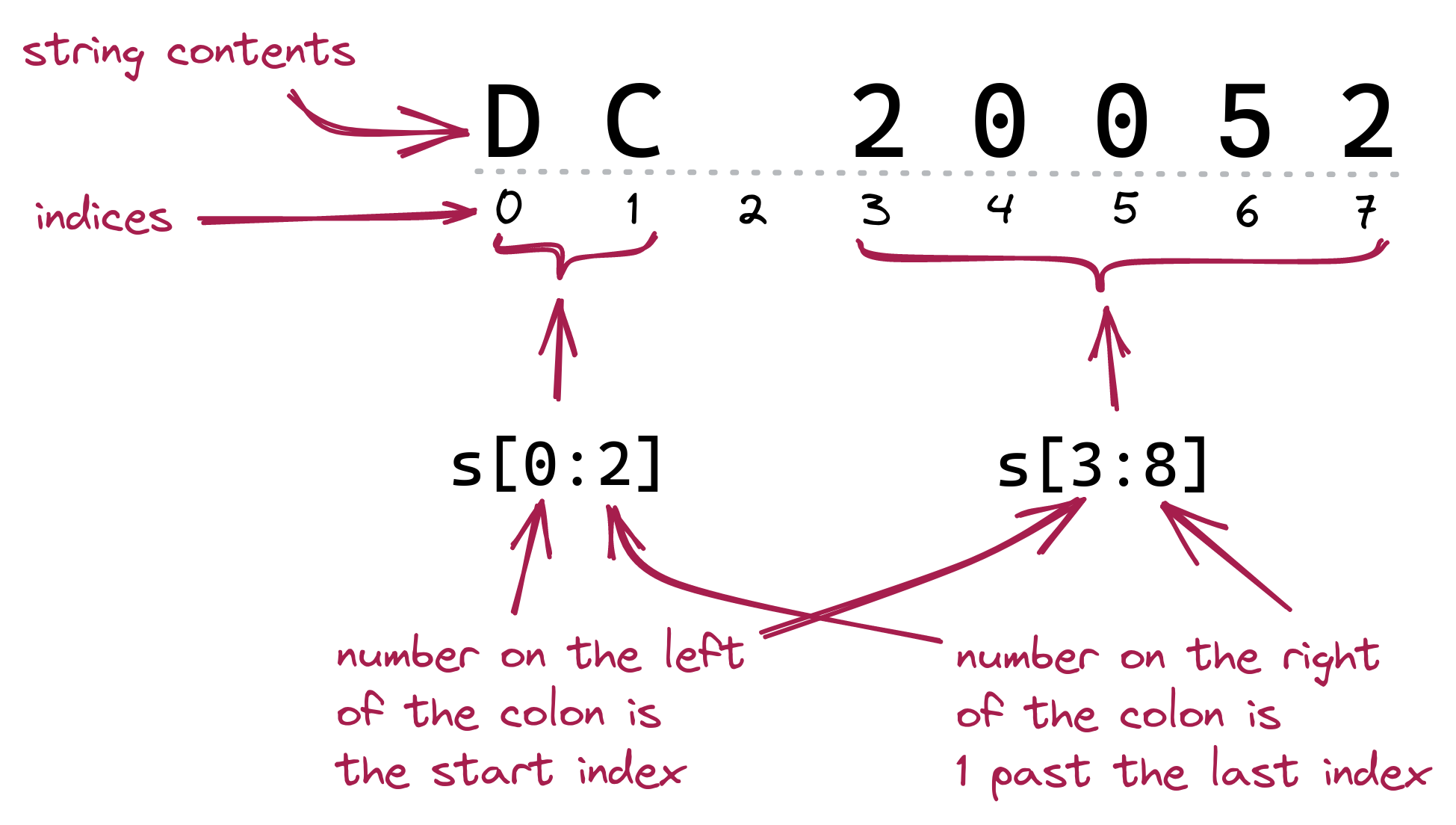
slicing

The slicing expression 0:2 refers to all the chars of the string from the first (the 0-th) up to just before the one at position 2 (which would mean 1).

0:2 refers to characters at positions 0 through 1. Similarly, 3:8 refers to all the chars from position 3 up to 7 (inclusive).
Recall: For any range of numbers like 3,4,5,6,7, exclusive would mean the numbers 4, 5, 6 (excluding 3, excluding 7). Inclusive would include the ends: 3,4,5,6,7.
Slicing ranges are specified so that the left end is inclusive and the right end is exclusive
- 3:8 means “starting at and including 3” and “going to but excluding 8”.
- 0:2 means “starting at and including 0” and “going to but excluding 2”.

Exercise 1.3.13

In slicing.py write code to extract the actual phone number (202)-994-4000 from

s = 'phone: 202-994-4000'
# Write your code here
# print the output

The printed output should be:

(202)-994-4000

Slicing expressions work for lists too:

A = ["'twas",'brillig','and','the','slithy','toves']
print(A[2:5])

['and', 'the', 'slithy']

Exercise 1.3.14

Type the above in slicing2.py and change the slice so that the output is:

["'twas", 'brillig']

Let’s look at slicing when we don’t know the size.

Consider the zipcode example where the 5-digit zip code may preceded by all kinds of text, as in:

'DC 20052'
'District of Columbia, 20052'
'20052'
'My zip code is 20052'

So, all we know is that the last 5 chars in the string need to be extracted. Then, we need to get the length of the string at the moment we have the string. Let’s put this in a function:

def extract_zip(s):
    start = len(s) - 5
    end = len(s)
    return s[start:end]

example1 = 'DC 20052'
example2 = 'District of Columbia, 20052'
example3 = '20052'
print(extract_zip(example1))
print(extract_zip(example2))
print(extract_zip(example3))

Note that

end = len(s)

gives us the index just past the last index. And

start = len(s) - 5

gives the index 5 position before the end. So, the slice becomes: s[start:end]

Exercise 1.3.15

In slicing3.py, write a function to extract the phone number in the same way, when the first part could be anything like phone: 202-994-4000 or my number is 202-994-4000.

In this case, use a function:

def slice_phone_number(s):
    # your code should take in a string s
    # and return a phone number formatted:
    #    (XXX)-XXX-XXXX
    return phone_number

Your function should return a string formatted as shown. The return value of slice_phone_number('phone: 202-994-4000') should be (202)-994-4000. The return value of slice_phone_number('my number is 202-994-4001') should be (202)-994-4001.

More Information Than You Require

Some advanced slicing syntax. Master the basic slicing syntax first.

We will use a simple list for these examples:

x = [1, 2, 3, 4, 5, 6, 7, 8]

A slice can leave a value to one side of the colon blank, such as x[1:] or x[:5]
- Leaving a value blank implies the first value if the left side is blank
- x[:5] yields [1, 2, 3, 4, 5]
- It implies the last value if the right side is blank
- x[2:] yields [3, 4, 5, 6, 7, 8]
Using a negative index in a slice will index from the end.
- -1 is the last element, -2 is the second-to-last, etc.
- This can be used for single values: x[-2] yields 7
- x[2:-2] yields [3, 4, 5, 6] (the second-to-last element, 8, is not included)
- x[-5:] yields [4, 5, 6, 7, 8]
Using a second colon slices using an interval greater than one:
- x[1:5:2] yields [2,4]
- Negative values index from the end of the list, backwards
- Going backwards includes the starting value and doesn’t include the stopping value.
- x[3:0:-1] yields [4, 3, 2]
- x[1:5:-1] yields [] - an empty list - going backwards from 1 already starts out after the stopping point!
- x[::-1] yields [8, 7, 6, 5, 4, 3, 2, 1]
- x[::] yields [1, 2, 3, 4, 5, 6, 7, 8] - but it’s faster to just use x 🙃

1.3.5 Using Slicing to Solve a Problem

Suppose we want to determine the longest prefix that two strings have in common, as in:

print(find_common_prefix('river', 'rivet'))

This should print ‘rive’ but

print(find_common_prefix('river', 'stream'))

should find no common prefix.

We will use the following ideas:

Let an index variable start at 0 and increase in a loop.
For each value of the index, we’ll compare the corresponding char in each string.
As long as the chars are equal, we keep going (because these will be part of the common prefix.)
The moment they are NOT equal, we will have gone past the end of the common prefix.

Let’s try this:

def find_common_prefix(w1, w2):
    for k in range(len(w1)):
        if w1[k] != w2[k]:
            break
    return w1[0:k]

print(find_common_prefix('river', 'rivet'))

The Python reserved word break is used to break out of a loop:

for k in range(len(w1)):
        if w1[k] != w2[k]:
            break

Thus, the moment break executes, execution exits the loop to the statement that follows the loop. Notice how we use slicing once we’ve found the char that’s past the common prefix:

return w1[0:k]  # All the chars from 0 to k-1 inclusive

Exercise 1.3.16

Does it work? Trace the execution of the above before typing it up in prefix.py to see.

Exercise 1.3.17

Next, trace the executing when the strings are ‘riveting’ and ‘rivet’. What goes wrong? Fix the problem in prefix2.py .

1.3.6 Built-in String Functions in Python

Python comes with many useful functions for strings.

Here’s a sample:

A = ['to','infinity','and','beyond','and', 'even','further']
s = 'infinity'

# Convert to uppercase:
print(s.upper())       

# Count occurrences of the char 'i' in s:
print(s.count('i'))    

# Locate which index 'f' first occurs in s:
print(s.find('f'))     

# Occurrences of 'and' in list A:
print(A.count('and'))  

# Occurrences of 'i' in 2nd string in list A:
print(A[1].count('i')) 

if A[3].startswith('be'):
    print('starts with be')

data = '42'
print(data.isnumeric())

Exercise 1.3.18

Type up the above in string_functions.py and examine the output to try and make sense of how the functions work.

There’s a key difference, for example, between the functions len() and upper():

s = 'hello'
k = len(s)
t = s.upper()

The function len() is like the ones we’ve been writing ourselves. In this case, the string s is given to it as a parameter:

k = len(s)

But the function upper() is quite different:

t = s.upper()

This is, in some sense, attached to the the string variable s. The use of the period right after the variable followed by a function is a somewhat advanced topic:

objects

We’ll just use the feature. (The advanced topic is called: objects.)

Let’s emphasize one more feature with this snippet of code:

s = 'hello'
t = s.upper()
print(s)
print(t)

Exercise 1.3.19

Type up the above in string_functions2.py and observe the output.

The string s itself did not change but its uppercase version was returned by the call

t = s.upper()

This returns a new string that gets placed into t.

Continuing with the earlier example: - Similar “dot” functions are available for lists too, as in:

k = A.count('and')

This asks the list A to count how many times the string 'and' occurs in the list.
The number that is returned gets stored in k. Notice how we can call a “dot” like function in a string when the string itself is an element of a list:

k = A[1].count('i')

Here, A[1] is the second string in the list A. - This happens to be 'infinity'. We’re calling its count() function. - And giving that function the character 'i' to count. - It returns a number, which gets stored above in k.

Consider the following partially completed code:

def get_zipcode(A):
    # Insert your code here

B = ['my','zip', 'is', '20052']
z = get_zipcode(B)
print(z+1)

Exercise 1.3.20

In string_functions3.py, complete the function above, assuming the fourth string in the list has the zipcode. Return a number, not a string, so that the print statement outputs 20053.

1.3.7 The Concept of “Type”

So far, we’ve seen different kinds of variables: Integer variables::

a = 100
b = 435

Floating-point variables for real numbers:

c = 3.14159
d = 2.718

String variables::

e = 'hello'    # String with multiple chars
f = 'h'        # Single-char string

Boolean variables:

g = False
h = True

Lists:

A = [1, 2, 3, 4]
B = ['gyre', 'gymbal', 'wabe', 0]

We’ve also seen other kinds of features or “things” in Python such as:

Reserved words.
Expressions, whether arithmetic, comparison, or Boolean.
Lists. Functions that we write using def.
Built-in functions like len() and print().
Control structures like for and if that direct the flow of execution.
Ways to use existing other code via import.

There happen to other kinds of “things” in Python:

One of these is another kind of variable called a “complex” variable, for advanced math. Another kind of “thing” or feature is an object which is a kind of structure that can contain related variables and functions (an advanced topic, it will not be tested in CSCI 1012)
Similarly, there are “things” called generators and iterators (an advanced topic, it will not be tested in CSCI 1012)

What we want to do here is focus your attention on a concept called type

At any given moment, a variable is said to have a type
What this means: what kind of value does it have at the moment? An integer? A string? Consider this:

x = 1      # The type of x is integer
y = 1.2     # The type of y is floating point
z = 'alarm'  # The type of z is string
b = False   # The type of b is Boolean

One can print the type of a variable as follows:

x = 1    
y = 1.2   
z = 'alarm'
v = False 
print(type(x), type(y), type(z), type(v))

The type information is often itself representation in a special Python feature called a class (intuitively, as in this “class of item”).

Exercise 1.3.21

In type.py, find out what gets printed by the above code.

Thus, we see that:

A variable that holds 1 is rightfully an integer variable.
A number like 1.2 is a floating-point number (what we’ve also called a real number), and so a variable that holds such a number is a floating-point variable.
A string variable that holds 'alarm' is just that, a string variable. And a variable that holds True or False is called a Boolean variable.

Converting from one type to another: - It is often useful to go from one type to another. - We’ve seen an example of going from single-char string to integer, and converting from int to string (and vice-versa).

To review, let’s look at a few more examples:

a = int(1.2)
b = float(3)
c = str(b)
d = int('256')
e = ord('x')
f = chr(97)
print(a, b, c, d, e, f)

Exercise 1.3.22

Type the above in type2.py,to see how it works.

Types and operators: Because our keyboards are limited in the number of symbol keys, we need to use some symbols for multiple purposes. The way we see this is when one operator, like +, has different meanings when used with different types:

a = 3
b = 4
c = a + b         # + for arithmetic

d = 'hello'
e = 'world'
f = d + ' ' + e   # + for string concatenation

Rather than list all possible uses of all operator symbols, we will introduce additional uses beyond the common case wherever appropriate. Generally, you should be intentional about using operators: you should know what the purpose is.

For example, consider:

a = 4
b = a * 3
print(b)          # prints 12

d = 'yes'
e = d * 3         # * for string concatenation
print(e)          # Prints yesyesyes

(The latter is not a frequently used operator with strings.)

1.3.8 A Text Application

Sometimes we need to go beyond what Python has to offer. One way to do this is to find a popular library and use that: What’s a library ? A library is a collection of programs all related for a purpose. For example, there’s a library called NLTK (go look it up) that’s aimed at processing English text: - It can figure out parts of speech from sentences. - It can pick out topics (somewhat approximately) in paragraphs. - It can group so-called stem-related words like “fry”, “fries”, “frying” and separate those from “friar”. However, installing and learning to use these sophisticated packages requires some work. What we will do instead in this course is to provide you with simple programs that you can download and use directly without any installation. - This is the purpose in providing programs like wordtool and drawtool.
Let’s use wordtool to find the longest sentence in a book: Wordtool has a feature to break down text and give you one sentence at a time. For example:

import wordtool as wt

sentences = wt.get_sentences_from_textfile('jabberwocky.txt')

count = 0
    
for s in sentences:
    count += 1
    print('Sentence #', count, ':\n', s, '\n', sep='')

Exercise 1.3.23

Type the above in sentence_app.py , to see how it works. You will need to download wordtool.py , wordsWithPOS.txt, and the sample text file jabberwocky.txt all into your module folder. You are likely to be familiar with the author’s other famous works.

Let’s point out: When using functions in another program, one has to import that program:

import  wordtool as wt

It is convenient to use a shorthand (such as wt) for an imported program: (We could have called it something other than wt). For example:

sentences = wt.get_sentences_from_textfile('jabberwocky.txt')

Wordtool asks you to name the file, expecting it to be a plain text file (not a Word file), and to initiate the process.

Exercise 1.3.24

What is the purpose of \n and what does sep='' do? You can look this up and try removing those in sentence_app2.py .

Let’s now do something interesting with wordtool: find the longest sentence (by length) in two texts to compare different author’s writing styles.

import wordtool as wt

def get_longest_sentence(filename):
    sentences = wt.get_sentences_from_textfile(filename)
    maxL = 0
    
    for s in sentences:
        if len(s) > maxL:
            maxL = len(s)
            maxS = s

    return maxS


book = 'federalist_papers.txt'
s = get_longest_sentence(book)
print('Longest sentence in', book, 'with', len(s), 'chars:\n', s)

print()

book = 'darwin.txt'
s = get_longest_sentence(book)
print('Longest sentence in', book, 'with', len(s), 'chars:\n', s)

Exercise 1.3.25

Type the above in sentence_app3.py. Then download darwin.txt (Darwin’s On the Origin of Species ) and federalist_papers.txt (the Federalist Papers by Hamilton and others). Which one has the longest? Who wrote the longest sentence in the Federalist Papers?

1.3.9 When Things Go Wrong

In each of the exercises below, first try to identify the error just by reading. Then type up the program to confirm, and after that, fix the error.

Exercise 1.3.26

def is_odd(k):
    if k % 2 == 1:
        return true
    else:
        return false

Identify and fix the error in error1.py .

Exercise 1.3.27

x = 4
if x >= 0 and <= 5:
    print('x is between 0 and 5 inclusive')

Identify and fix the error in error2.py .

End-Of-Module Problems

Full credit is 100 pts. There is no extra credit.

Problem 1.3.1 (60 pts)

Write a function common_denominator.

The function should take three arguments, all integers.
The function should determine if these three integers have a common denominator other than 1.
- Two numbers have a common denominator if they both divide evenly by the same number.
- 6 divides evenly by 2 and 3; 14 divides evenly by 2 and 7. 6 and 14 have a common denominator: 2.
- 21 divides evenly by 3 and 7; 20 divides evenly by 5, 2, 4, and 10. 21 and 20 therefore do not have a common denominator.
If all three integers have a common denominator, the function should return True.
- If they do not, the function should return False.
For this problem, a number is not its own denominator.
The integers will always be positive.

Examples:

common_denominator(3, 4, 5) should return False.
common_denominator(21, 24, 30) should return True.
common_denominator(2, 4, 6) should return False.
common_denominator(4, 6, 8) should return True.

Submit as common_denominator.py.

Problem 1.3.2 (60 pts)

Write a function after_midnight.

The function should take one argument: a string.
If the string contains the substring "midnight":
- Return the remainder of the string: everything that comes after "midnight".
If not:
- Return False.

Examples:

after_midnight("You burn with hunger for food that does not exist.") returns False.
after_midnight("Five minutes to midnight.") returns string ".".
after_midnight("The ice sculptures at the midnight buffet often look hurredly carved.") returns " buffet often look hurredly carved."

Each input string will contain the substring "midnight" no more than one time.

Submit as after_midnight.py.

Problem 1.3.3 (60 pts)

Write a function capitalizer.

The function should take one argument: a string.
- The string will represent English text.
If there are any instances of the word i, change them to I in the string.
Return the string.

Examples:

capitalizer("i know you know") returns "I know you know"
capitalizer("Good idea!") returns "Good idea!".
capitalizer("that's what i meant") returns "that's what I meant".
capitalizer("both you and i") returns "both you and I".

Hint: There are three distinct cases: i appearing at the beginning, the end, and in the middle of the sentence.

Submit as capitalizer.py.

Problem 1.3.4 (60 pts)

Write a function fix_spacing.

The function should take one argument, a string.
- The string will represent English text, several sentences.
- Sentences will always end with a period.
Some sentences will have two spaces after each period. Others will have one space.
- The last sentence will not have any spaces after the period.
Return the same string, but with one space after every period (except for the last).

Examples:

fix_spacing("Great job. I agree. Approved.") returns "Great job. I agree. Approved.".
fix_spacing("I see what you did there. Don't do it again.") returns "I see what you did there. Don't do it again.".

Submit as fix_spacing.py.