Objectives
By the end of this module you will be able to:
- Understand how a list is different from a variable
- Explore the syntax around using lists in programs
- Use lists in programs to solve problems
- Practice mental execution (tracing) and debugging related to lists
1.0.0 Basic List Example
Consider this program:
# List example:
A = [1, 4, 9, 16, 25]
for i in range(5):
print(A[i])
# In contrast, a plain variable:
k = 100
print(k)
Exercise 1.0.1
In list1.py, type up the above and examine the output. Then, inside the above for loop, but before the first print statement, add an additional line of code to also print the value of i so that each value of i is printed on a line by itself.
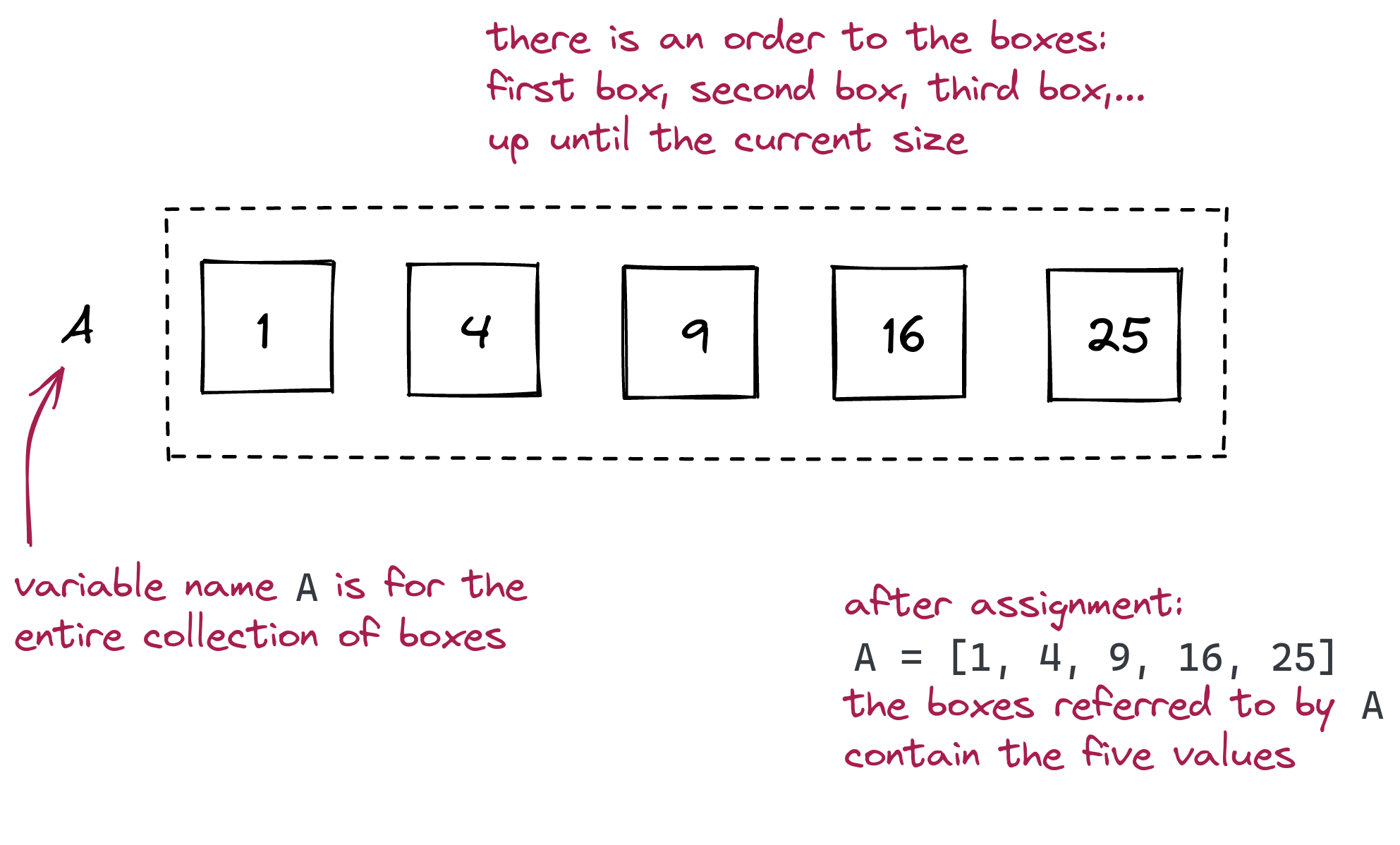
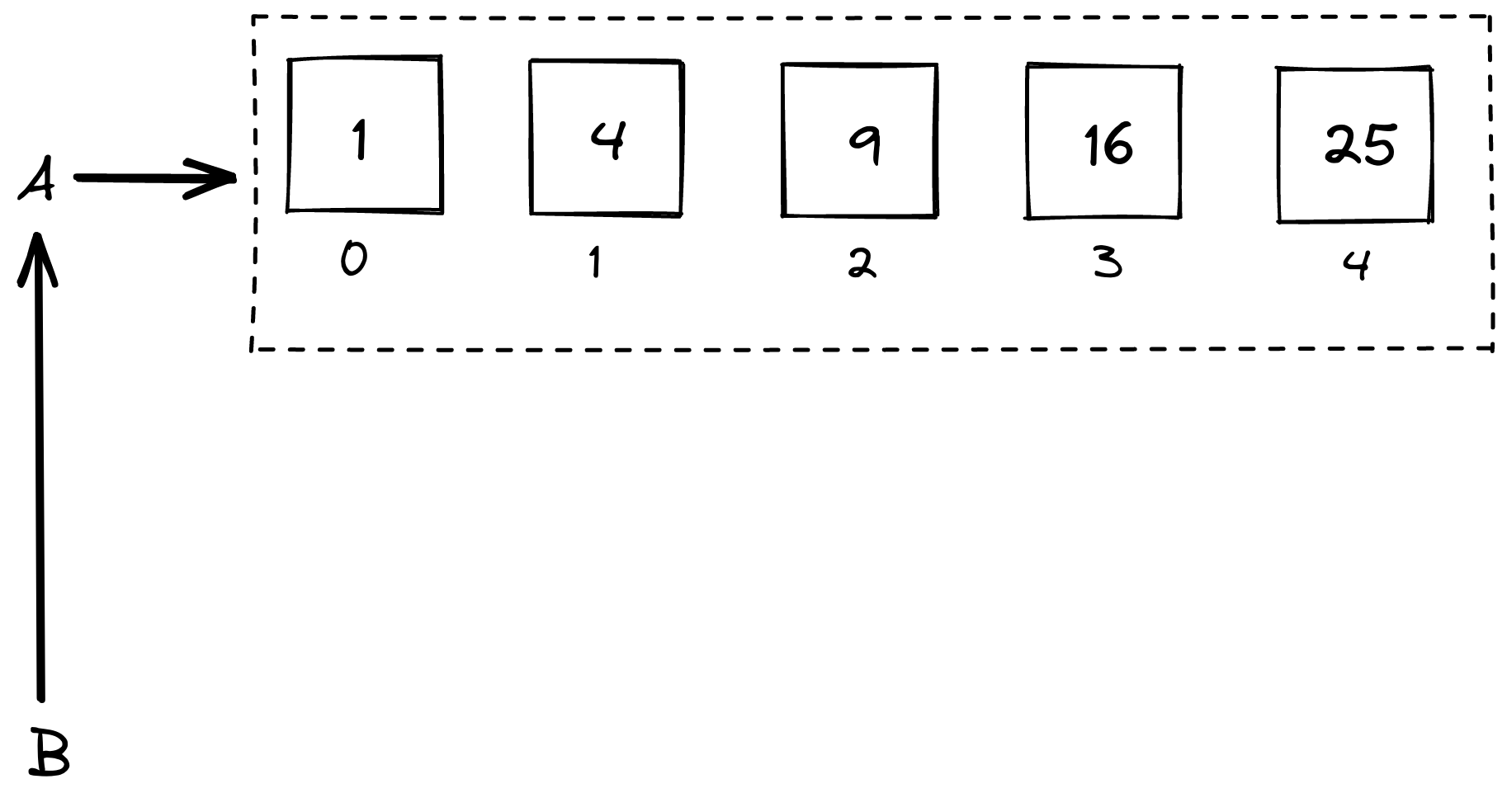
Remember how we think of a variable as a box that stores values? - This is indeed how we think of the variable k above.
- In contrast, a list variable is a single name given to a collection of boxes:
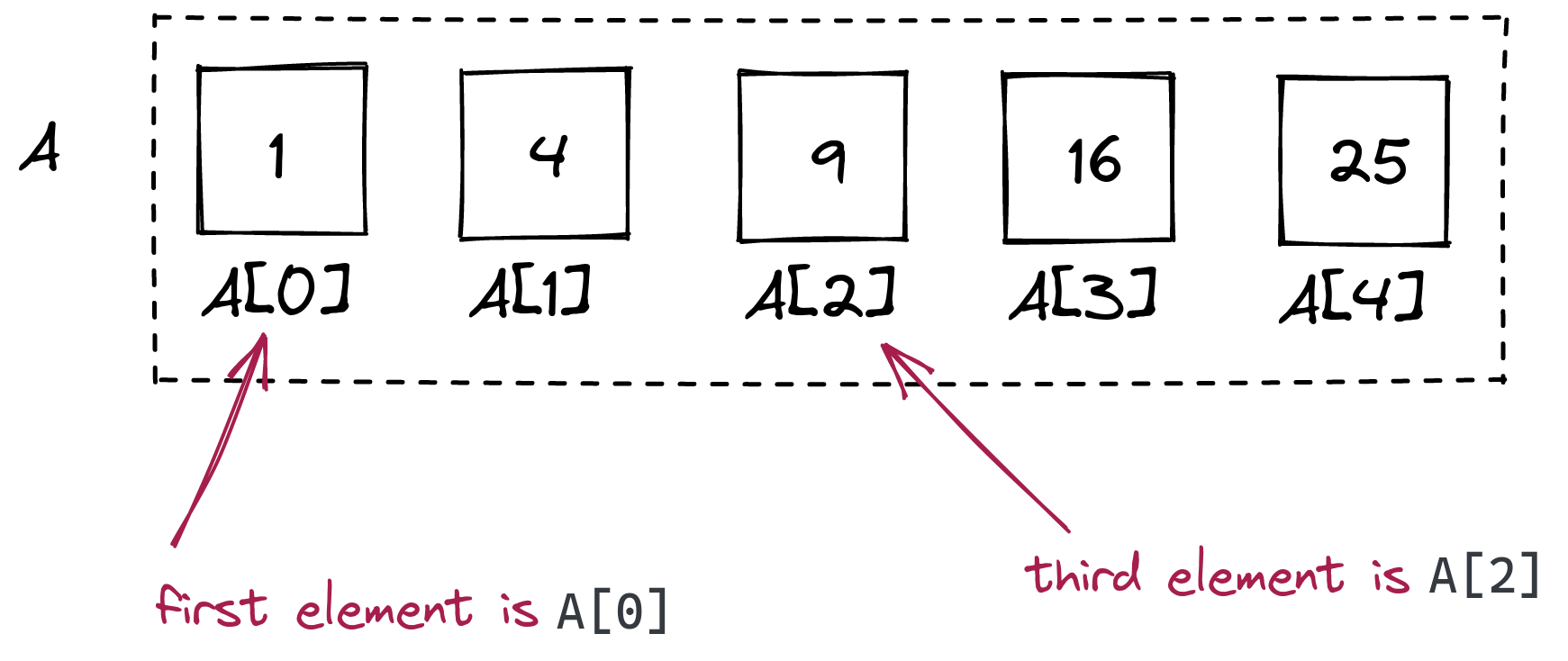
- The above collection has a current size, in this case 5. The values in a list are called elements of the list. There is an implied order going from the first to the last element. It turns out, we can access individual elements in the list using indices:
List indices start at 0 and end at one less than the size. In the above example, the size of the list is 5, so the indices (positions in the list) are: 0, 1, 2, 3, 4.
Consider this program:
A = [1, 4, 9, 16, 25]
# Use len to get the current size:
n = len(A)
print('Size of A: ' + str(n))
# Add an element to the list (and the end):
A.append(36)
n = len(A)
print('Size of A: ' + str(n))
# Change a particular element:
A[3] = 100
print('The list: ' + str(A))
Size of A: 5
Size of A: 6
The list: [1, 4, 9, 100, 25, 36]
Exercise 1.0.2
Try out the above in list2.py.
Let’s point out:
- Observe how we obtain the current size and add an element:
- Next, observe square brackets being used for different purposes:
- We could use a variable to access elements, as long as that variable has an integer value that has a valid index, for example:
Remember len ? We had used len earlier for the length of strings, as in
s = 'hello'
print(len(s)) # Prints 5
Here, len works to give us the length of a list, as in:
A = [1, 4, 9, 16, 25]
print(len(A))
For example:
A = [1, 4, 9, 16, 25]
i = 3 # i's value 3 is valid for a size 5 list
print(A[i])
i = 7 # 7 is not valid
print(A[i])
In the above example, there is no element A[7] in a list that only has 5 elements.
Exercise 1.0.3
Type up the above in list3.py.
Exercise 1.0.4
In list4.py, make a list with the values 1,2,3,4,5,10,11,12,13,14. Then, set up a for loop so that only the odd numbers are printed as in:
The output should be:
1
3
5
11
13
1.0.1 More List Examples
Just as we can add elements to list, so can we remove elements, as in:
A = [64, 9, 25, 81, 49]
print(A)
A.remove(9)
print(A)
Exercise 1.0.5
Confirm the output by typing up the above in list5.py. Explore what would go wrong if you try and remove something that’s not in the list. For example, change the line A.remove(9) to A.remove(10).
Using append adds an element to the end of a list.
x = [4, 1, 2, 1]
x.append(3)
print(x)
Using remove removes the first instance of that item from the list.
x = [4, 1, 2, 1]
x.remove(1)
print(x)
- The elements in a list do not need to be in sorted order, as the above example shows. They can be in any order, but once in that order, they stay in that order unless we make a change to the elements in the list.
- Although our examples so far have lists of integers like 64, we will later build lists with real numbers and strings.
Consider this example:
# List constructed by typing the elements in:
A = [1, 4, 9, 16, 25]
print(A)
# List built using code to construct elements:
B = [] # An empty list
for i in range(5):
k = (i+1) * (i+1)
B.append(k)
print(B)
- Trace through the changing values of
i, k and the list B in each iteration of the for loop.
Exercise 1.0.6
Type up the above in list6.py and verify the trace.
It is possible to create an empty list and give it a variable name as in:
We could then add elements by appending them. One can shorten the lines inside the loop:
B = [] # An empty list
for i in range(5):
B.append( (i+1) * (i+1) )
Here, we’ve fed the arithmetic expression (i+1) * (i+1) directly into append, without using a separate variable k to first calculate and then append.
Exercise 1.0.7
In odd_list.py fill in the necessary code below to create a list with the first N odd numbers:
N = 10
odd_numbers = []
# WRITE YOUR CODE HERE
print(odd_numbers)
In this case, the output should be:
[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]
(These are the first 10 odd numbers).
We do not need to traverse in exactly the order of elements in the list: For example:
A = [15, 25, 35, 45, 55, 65, 75, 85, 95, 105]
for i in range(9, 0, -2):
print(A[i])
- Here, we’re starting at the last element, traversing the list from end to beginning in steps of 2.
Exercise 1.0.8
Trace through the above code showing the values of i and A[i] at each iteration. Confirm by typing your code in list7.py.
1.0.2 Copying Lists
Let’s first look at copying between regular variables, as in:
x = 5
y = x # Copy the value in x into y
x = 6 # Change the value in x
print(y) # Does it affect what's in y?
Exercise 1.0.9
Write the above as var_copy.py and examine how variables do or do not change based on assignment.
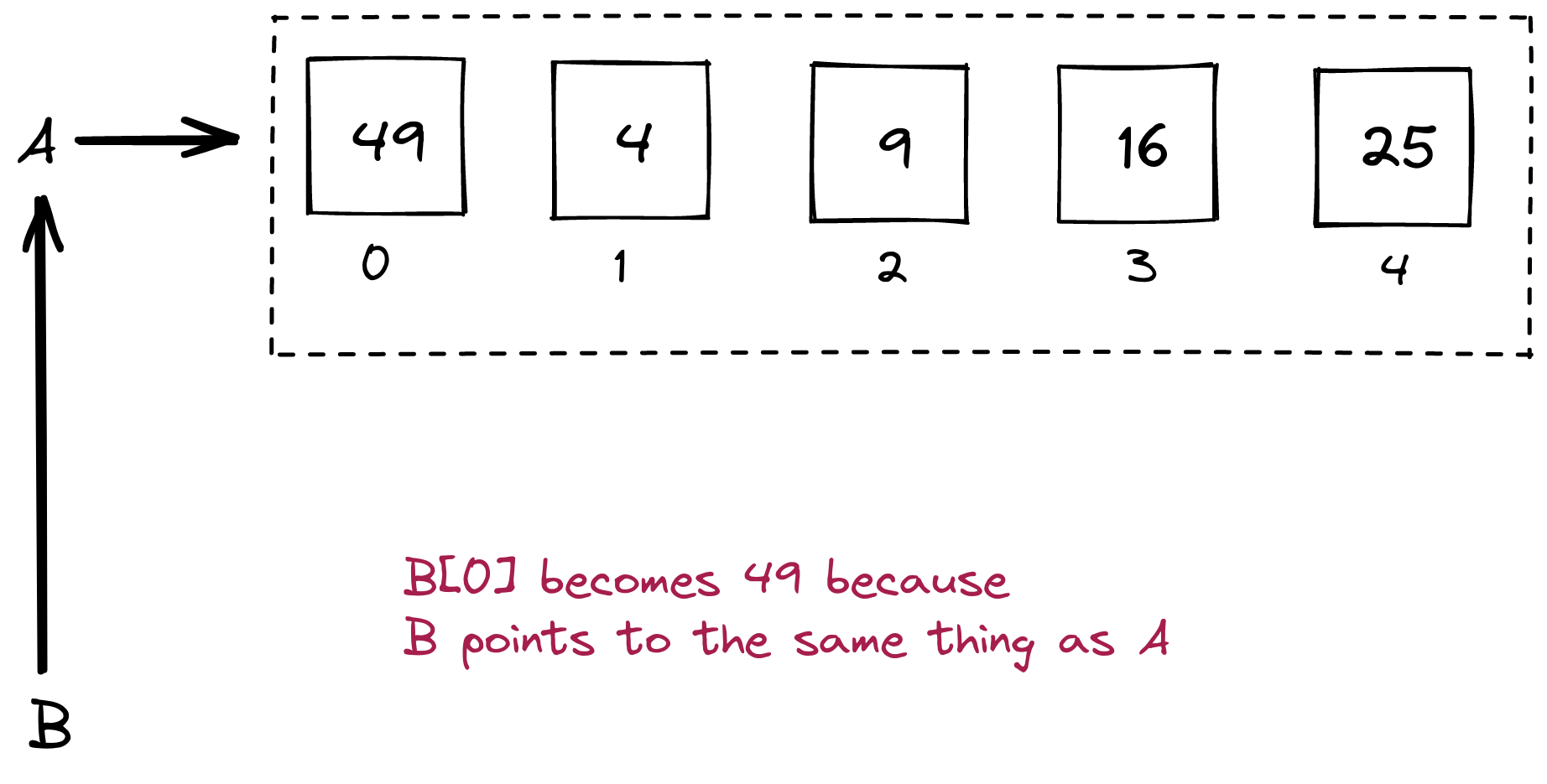
Next, consider this:
A = [1, 4, 9, 16, 25]
B = A
A[0] = 49 # Change some value in list A
print(B) # Does it affect what's in list B?
Exercise 1.0.10
Type up the above in list_copy.py to find out whether any values have changed in list B.
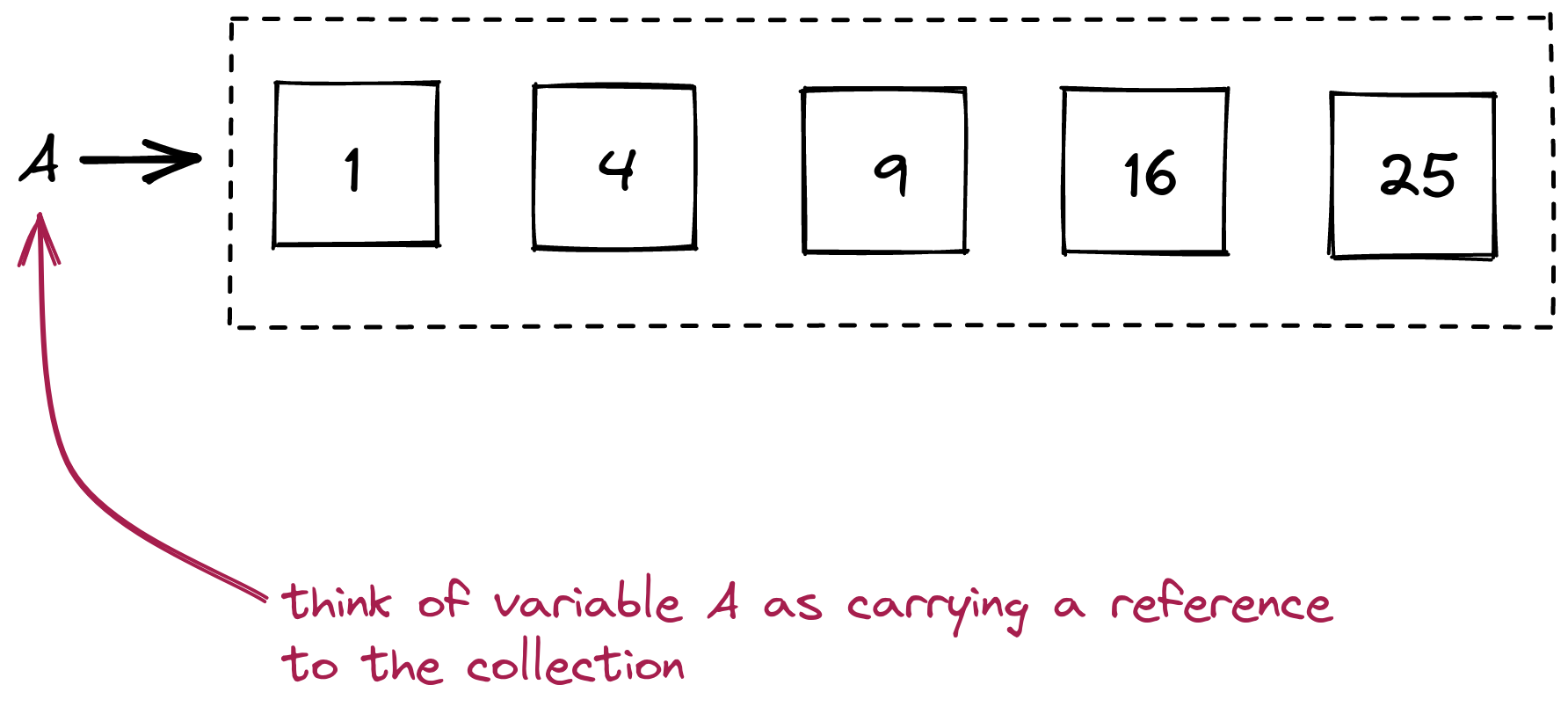
Clearly something different is going on with lists. One way to think of it is to go back to our picture of a list:
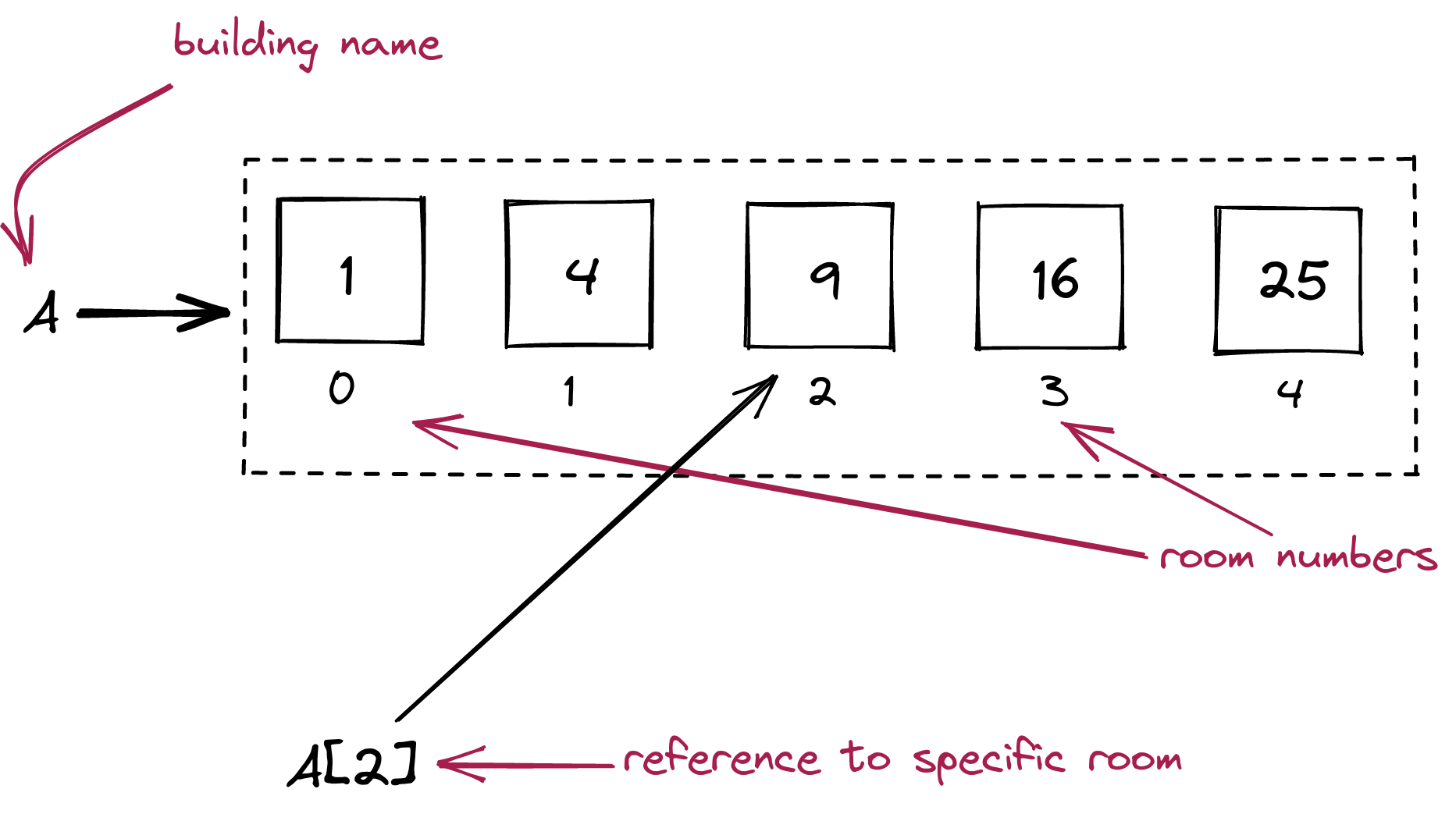
We’ll now sketch out an analogy: Think of the list as a building, with rooms (the boxes):
- Then, the list variable
A is really something that holds the building address (the building number).
- The rooms in the building are numbered from 0, 1, etc.
- The first room is
A[0], the second is A[1] etc. Now, consider an assignment like:
Then, in the building analogy, what we get is:
This is why, when we change the A list as in
A[0] = 49 # Change some value in list A
This produces:
The “building” analogy refers to the computer’s memory. List names like A and B reference places in the computer’s memory. The code
tells Python that B should reference the same place in memory as referenced by A.
For this course, it’s enough to simply understand that lists are collections, and to get comfortable with the idea that two named lists can reference the same data.
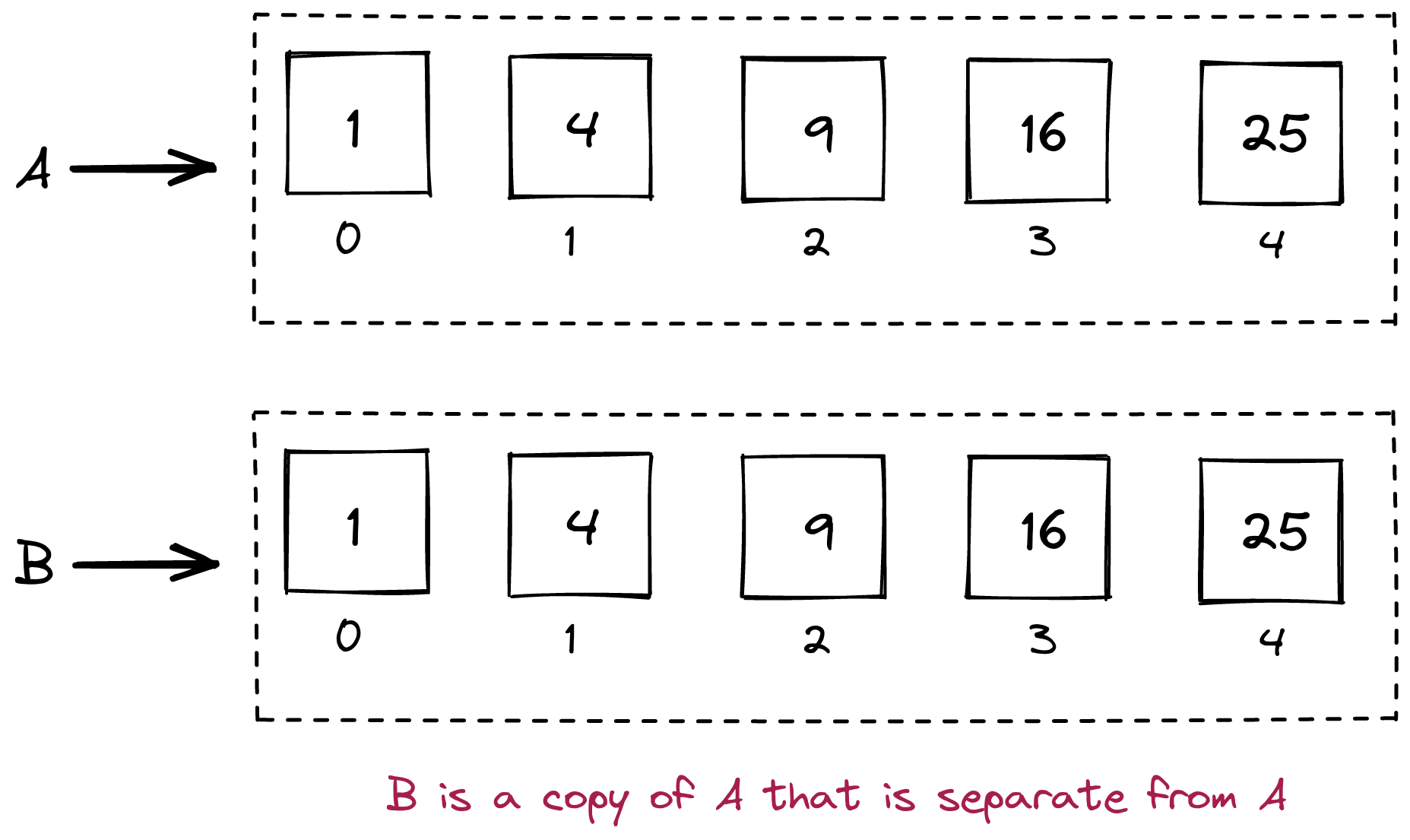
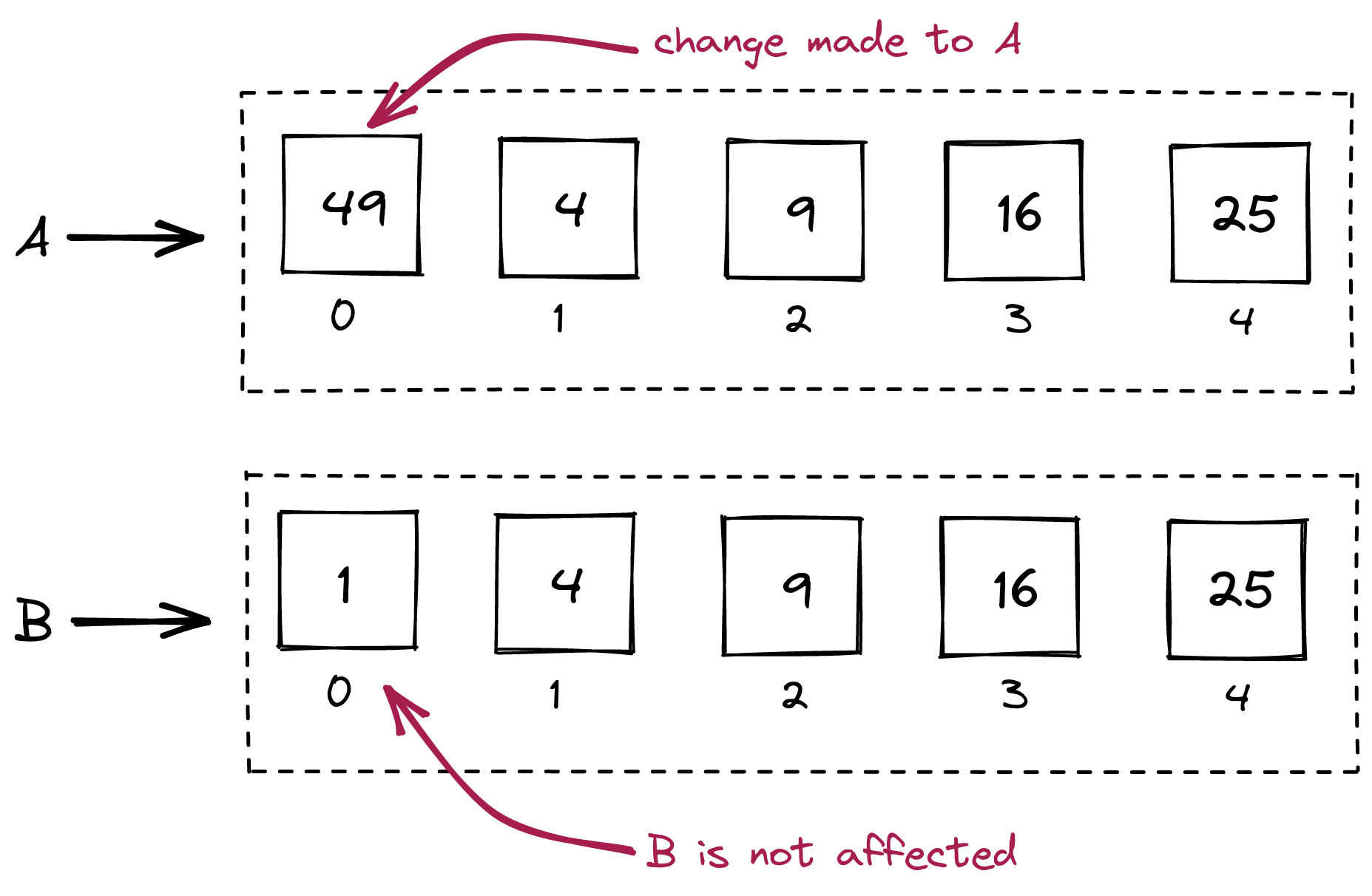
We obviously want to know: is it possible to create a complete copy of A in B? As in:
Because then, if we change A, it does not affect B:
This is what it looks like in code:
A = [1, 4, 9, 16, 25]
B = A.copy()
A[0] = 49 # Change some value in list A
print(B) # Does it affect what's in list B?
Exercise 1.0.11
Type up the above in list_copy2.py to find out if any values have changed in list B.
So, which of B = A or B = A.copy() do we use?
Generally, you should use B.copy() unless you intentionally want the same “building number”.
In the former case, you have to be careful.
1.0.3 Iterating Through Lists
Consider this example:
A = [1, 3, 5, 7, 9]
total = 0
for i in range(5):
total = total + A[i]
print(total)
Exercise 1.0.12
Type up the above in total_example1.py.
Now let’s look at two different ways of writing the same loop (we’ll only show the loop part):
The first way:
for i in range(len(A)):
total = total + A[i]
Notice: Instead of figuring out the length of a list by looking at the list, we can ask Python to compute the length of A and use it directly using len(A) - This way, we don’t need to track the length ourselves (if elements get added or removed). The second way is even better:
for k in A:
total = total + k
Here: - Here the iteration is directly over the contents of the list. - The variable k is not an index but takes on the actual values in the list. With a list like
A = [1, 3, 5, 7, 9]
total = 0
for k in A:
total = total + k
- In the first iteration,
k is 1, in the second, k is 3, in the third, k is 5, and so on. These get added directly into the variable total.
- You can think of the first approach (using an index
i and A[i]) as index iteration. The second (using the value directly), as content iteration. Which one should one use?
- Prefer to use content-iteration, whenever you can. In some cases, however, you’ll find index iteration is useful, especially when you need the position where something occurs in the list.
Exercise 1.0.13
In content_iteration.py, use content-iteration to print the contents of the list A below:
A = [2020, 2016, 2012, 2008, 2004, 2000]
# Write your code here:
The output should be one number per line in the order that the numbers appear in the list.
There is a way to use both kinds of iteration together using the function enumerate:
names = ['Cedric', 'Omar', 'Eva', 'Marcel', 'Jon']
for i, name in enumerate(names):
print("Index: ", i)
print("Name: ", name)
Index: 0
Name: Cedric
Index: 1
Name: Omar
Index: 2
Name: Eva
Index: 3
Name: Marcel
Index: 4
Name: Jon
This is an “advanced” method (and not one required for this course).
Master the basic forms of iteration before using it.
1.0.4 Multiple Lists
Suppose we have two lists of the same length like this:
A = [1, 4, 9, 16, 25]
B = [1, 3, 5, 7, 11]
Let’s examine different ways of performing addition on the elements.
First, let’s add up the total of all 10 numbers:
A = [1, 4, 9, 16, 25]
B = [1, 3, 5, 7, 11]
total = 0
for k in A:
total = total + k
for k in B:
total = total + k
print(total)
- Trace the values of
k and total in each iteration of each loop.
Exercise 1.0.14
Type the above in twolist1.py to confirm the trace.
Note: In the above case, we added all the numbers contained in both lists, to get a single number. Notice how natural it is to use content-iteration. What if we want a third list whose elements are the additions of corresponding elements from each list?
1 4 9 16 25
1 3 5 7 11
-----------------------
2 7 14 23 36
Here, the last row is a new (third) list. Let’s write code to perform element-by-element addition:
A = [1, 4, 9, 16, 25]
B = [1, 3, 5, 7, 11]
C = []
for i in range(5):
element_total = A[i] + B[i]
C.append(element_total)
print(C)
- Trace the values of
i and element_total in each iteration of the loop, and also show how the list C changes across the iterations.
- How would your code change if you iterated over the contents of the lists, rather than the index variable
i?
Exercise 1.0.15
Type the above in twolist2.py to confirm the trace. Print C inside the loop, by adding a print statement right after the append occurs.
1.0.5 Moving Elements Within A List
Consider a list like:
Next, suppose we want to swap the elements in the 2nd and 4th positions within the same list (not creating a new list). That is, we want to write code so that:
A = [1, 4, 9, 16, 25]
# ... code to swap 2nd and 4th elements ...
print(A)
# Should print [1, 16, 9, 4, 25]
To achieve that, we use a temporary variable
A = [1, 4, 9, 16, 25]
temp = A[1]
A[1] = A[3]
A[3] = temp
print(A)
(The temporary variable is called temp in the example, but the variable name could be anything we choose.)
Exercise 1.0.16
Write the above code as variable_swap.py.
Replace the middle three lines with:
This should illustrate why the temporary variable is useful.
Exercise 1.0.17
Use the temporary variable idea to perform a left-rotate of a list in left_rotate.py. Given:
A = [1, 4, 9, 16, 25]
# ... your code here...
print(A)
# Should print [4, 9, 16, 25, 1]
Everything but the first element moves leftwards and the first element gets to the last place. Use a for loop to move most (but not all) elements.
1.0.6 Lists of Strings, Characters, and Real Numbers
One can make a list of any variable type.
For example:
# A list of strings:
A = ['cats', 'and', 'dogs']
s = ''
for w in A:
s += w
print(s)
# A way to extract the characters in a string into a list:
s = 'abcdef'
B = list(s)
print(B)
# Some real numbers:
C = [1.1, 2.22, 3.333, 4.4444]
total = 0
for x in C:
total = total + x
print('Average =', total/4)
Exercise 1.0.18
Type the above in other_lists.py, while noticing the subtle change in how the last print statement is written. Insert spaces in the first loop so that the first thing printed is cats and dogs (note the trailing space).
1.0.7 A Different Version of print
Consider these two variations of using print:
i = 100
j = 'years'
k = 'of'
l = 'solitude.'
print(str(i) + ' ' + j + ' ' + k + ' ' + l)
print(i, j, k, l)
Exercise 1.0.19
Type the above in print_example.py,
- The first version above uses string concatenation to send one big string to print:
print(str(i) + ' ' + j + ' ' + k + ' ' + l)
- In the second version above, strings and variables given to print are separated by commas. Here, print treats the four things as separate entities:
In the first case, print automatically inserts a space between the different items (that are separated by commas).
In the second type, there is no need to convert numbers to strings.
1.0.8 Random Selection of Elements from a List
It is often useful to be able to pick random elements from a list.
Let’s use this feature first for a single roll of a die, and then two dice (we will use 6-sided dice):
Since a single die has 6 faces with the numbers 1 through 6, we’ll use a list of the numbers 1 through 6:
Our goal is to choose one of these numbers randomly. Python provides a way to randomly pick (without removing) an element from a list:
die = [1, 2, 3, 4, 5, 6]
roll = random.choice(die)
Let’s put this together into a program (remembering to import the random package):
import random
die = [1, 2, 3, 4, 5, 6]
roll = random.choice(die)
print(roll)
Exercise 1.0.20
Type the above in die_roll.py. Run the program several times to see that you are getting random selections from the list.
Next, let’s use this to simulate an extraordinarily simple game:
- Two players each roll a die
N times.
- The numbers on the rolls are averaged.
- The player with the higher average wins.
Not particularly entertaining, but an easily-written program.
import random
die = [1, 2, 3, 4, 5, 6]
num_trials = 10
total = 0
for i in range(num_trials):
roll = random.choice(die)
print(roll)
total += roll
print('Average score:', total/num_trials)
Exercise 1.0.21
Type the above in die_roll2.py to observe the result.
Exercise 1.0.22
In die_roll3.py, change the game to the following: in each trial, each player rolls the die twice and adds the two numbers. The final score is the average across all trials.
1.0.9 Some Math With Programming
Let’s start with an example and then use that to delve into a few concepts:
from drawtool import DrawTool
dt = DrawTool()
dt.set_XY_range(0,10, 0,100)
# The blue collection of points:
dt.set_color('b')
x_coords = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y_coords = [3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23]
dt.draw_curve_as_points(x_coords, y_coords)
# The red collection of points:
dt.set_color('r')
x_coords = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y_coords = [0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100]
dt.draw_curve_as_points(x_coords, y_coords)
dt.display()
Exercise 1.0.23
Type up the above in plot_example.py to see what you get. You will also need to download drawtool.py into the same folder
First, let’s ask some basic questions:
What, really, is a graph and what does it mean to plot on a graph?
What are \(x\) and \(y\) values and what do they have to with plotting?
What’s a function and what’s the connection between \(f(x)\) and points on a graph?
And what does this have to do with programming? We’ll address these questions below.
We began with natural numbers (positive whole numbers) like 1, 2, 3, etc.
Along with them came operations like addition, subtraction, multiplication and division. (Ancient applications: agriculture, accounting, trade, time-keeping).
The natural numbers were not enough: one can perform \(3 - 8\) and get a negative value. So came the negatives (like -5), forming the set of integers: \(\{..., -3, -2, -1, 0, 1, 2, 3, ...\}\)
Then, because \(5 \div 2\) is not an integer, more numbers were needed, hence real numbers.
- This includes rational numbers like \(\frac{5}{2} = 2.5\) and irrational numbers like \(\sqrt{2}\)
- We do not deal with irrational numbers in programming.
Next came algebra:
Instead of saying “I can take 12 times 4 and get 48, and then divide by 6, to get twice your original number 4”, we can write: \(\frac{12x}{6} = 2x\)
- It’s much more compact and precise.
Next came functions:
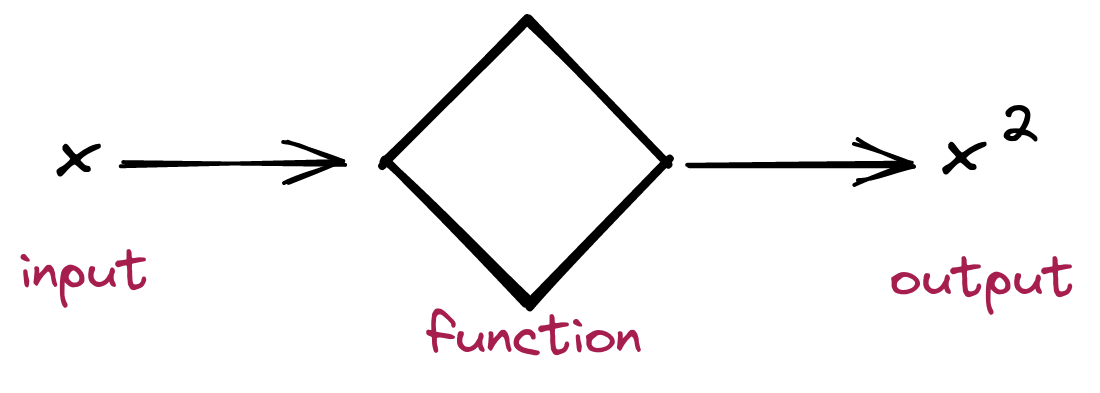
Instead of saying “Take your number and multiply it by itself”, it’s much more compact to say: \(f(x) = x^2\). We can think of a function as taking some input \(x\) and “doing something to it” to get an output.
- All of this resulted in significant advances in mathematics.
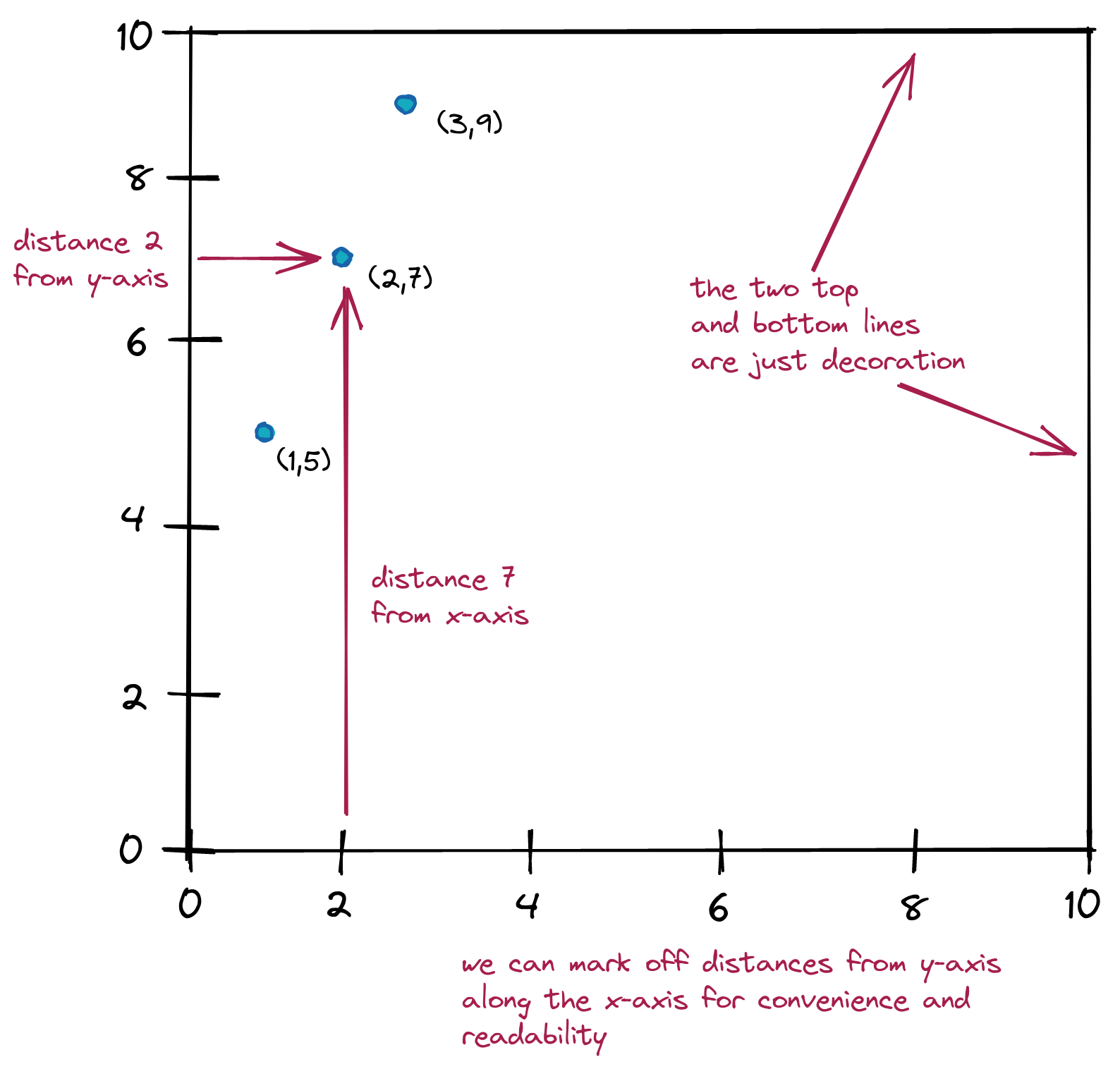
Descartes introduced coordinates. The idea of coordinates:
- Suppose you had a way of linking or associating pairs of numbers:
- For example, suppose 1 is associated with 5
- 2 is associated with 7
- 3 with 9
- We can write these as: (1,5), (2,7), (3,9) and so on.
- Next, draw two perpendicular lines (one horizontal, one vertical) on a page:
Call them the \(x\) and \(y\) axes respectively.
- Now given associations (1,5), (2,7) and (3,9):
- Treat the first number as the distance from the vertical axis.
- Treat the second number as the distance from the horizontal axis.
- This will put us in a unique spot.
- Call that a point. For example:
- That’s all there’s to it. This simple idea was transformational.
The connection between functions and coordinates:
Suppose you have a function like: \(f(x) = 2x + 3\) One way to make sense of a function is to compute lots of examples like:
- \(f({\bf 1}) = 2*{\bf 1} + 3 = 5\)
- \(f({\bf 2}) = 2*{\bf 2} + 3 = 7\)
- \(f({\bf 3}) = 2*{\bf 3} + 3 = 9\)
- And even \(f({\bf 3.16}) = 2*{\bf 3.16} + 3 = 9.32\)
A pair of axes makes it possible to visualize a function directly, initially by plotting some example points:
Take some \(x\).
Calculate \(f(x)\)
Then treat \(x\) as the first coordinate (distance from y-axis).
Treat \(f(x)\) as the second coordinate (distance from x-axis), and plot.
For example, when \(x=2\), then we saw that \(f(2) = 7\).
In general, we want to plot \(x, f(x)\) for lots of different possible \(x\) values.
Here, \(f(x)\) is what we use for the y-coordinate, which is why we sometimes write \(y = f(x)\).
When we plot \(x, f(x)\) for different \(x\) values,we typically pick those \(x\) values for our convenience.
Above, we showed how to calculate \(f(x) = 2x + 3\) when \(x=1\), \(x=2\),\(x=3\), and so on, perhaps up to when \(x=10\).
But if we need to, we could just as easily calculate \(f(x) = 2x + 3\) when \(x=0.1\), when \(x=0.2\), when \(x=0.3\), and so on up to when \(x=1.0\)
Let’s put these ideas to use: Suppose we have two functions \(f\) and \(g\)
- \(f(x) = 2x + 3\)
- \(g(x) = x^2\)
Our goal: compare the two functions. One advantage of programming is that we can write code to perform the action of functions. For example:
for x in range(11):
f = 2*x + 3
print('x =', x, ' f(x) =', f)
for x in range(11):
g = x*x
print('x =', x, ' g(x) =', g)
Exercise 1.0.24
Type up the above in function_example.py.
It is far more valuable to visualize, so let’s set about plotting both together: To plot, we’ll need to construct the list of x and y coordinates:
from drawtool import DrawTool
dt = DrawTool()
dt.set_XY_range(1,10, 0,100)
x = 0
x_coords = []
y_coords = []
for i in range(11):
x_coords.append(x)
f = 2*x + 3
y_coords.append(f)
x = x + 1
dt.draw_curve_as_lines(x_coords, y_coords)
dt.set_color('r')
# WRITE CODE HERE for the second function
dt.draw_curve_as_lines(x_coords, y_coords)
dt.display()
Exercise 1.0.25
Type up the above in function_plot.py and add code for the second function \(g(x)=x^2\) to get a plot like:
Scale and axes: You may have noticed that the x-axis above had tick marks going from 0 to 10, while the y-axis went from 0 to 100. This is an example of a plot that’s NOT drawn to scale. Let’s draw one to scale to see what it looks like by changing one line, from
dt.set_XY_range(1,10, 0,100)
to
dt.set_XY_range(0,100, 0,100)
Exercise 1.0.26
In function_plot2.py change your code from the earlier exercise to make the scale the same along x and y axes.
When to use different scales along the axes:
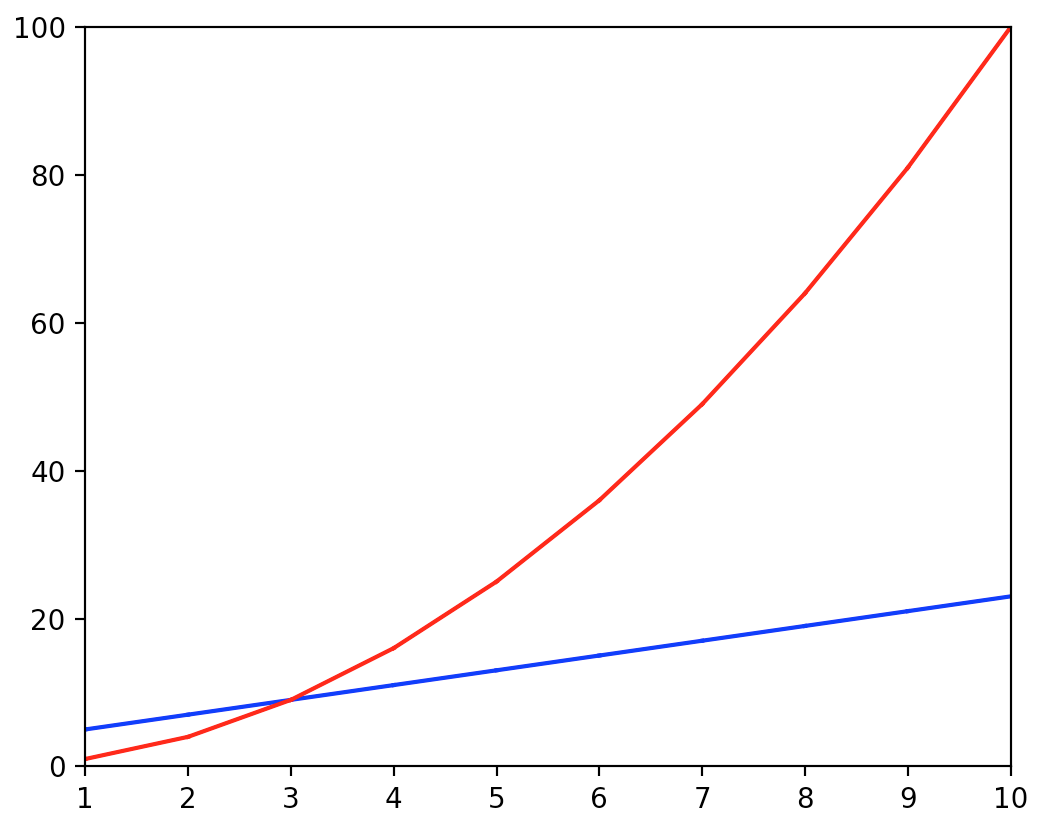
- Using the same scale, we see the dramatic difference between linear growth (the function \(f(x)=2x+3\)) and quadratic growth (the function \(g(x) = x^2\)).
- But at the same time, some features like the point of intersection of the two curves is hard to see.
- We can use different scales when we want to emphasize different aspects.
Exercise 1.0.27
In function_plot3.py,add a third function \(h(x) = 2^x\).
Plot and take a screenshot once with the x and y range both as [0, 1200], and once with the x-range as [0,12] and the y-range as [0,1200].
This should show you how slow quadratic growth is compared to exponential growth.
1.0.11 When Things Go Wrong
In each of the exercises below, first try to identify the error just by reading. Then type up the program to confirm, and after that, fix the error.
Exercise 1.0.28
A = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
for i in range(1, 10):
print(A[i])
Identify and fix the error in error1.py.
Exercise 1.0.29
The following program intends to build the decreasing-order list [10, 9, 8, 7, 6, 5, 4, 3, 2, 1].
A = []
n = 10
for i in range(n):
n = n - 1
A.append(n)
print(A)
Identify and fix the error in error2.py.
Exercise 1.0.30
The following program intends to add to N all the elements of the list A.
N = 100
A = [1, 4, 9, 16, 25]
for k in A:
N = N + A[k]
print(N)
Identify and fix the error in error3.py.
1.0.12 The Big Picture
This is the next installment in our series of stepping back from it all and reflecting, with the hope of helping you progress as a learner.
This time our topic is math and math anxiety.
Let’s start by acknowledging a few things:
Students do in fact have bad experiences learning math.
- For example, if you were unlucky to be ill during the critical period in 4th grade when fractions are covered, that could become a gap that precludes other concepts.
- Or if algebra did not go well, everything that follows in math can lead to cascading difficulties in learning. Students learn math differently and their “window of opportunity” may not be aligned with where their school is.
- Thus, for many students, a certain age is not optimal for academic intensity, or issues at home prevent full engagement. There are hidden cultural dispositions that can get in the way.
- The most pernicious by far is the notion that some people just aren’t cut out for it. Or you have to have the “math gene”.
At the same time, there’s good news:
Math (and programming) is like any other skill: everyone can acquire it with sufficient practice, but not everyone can reach the level of “world expert”.
This is true of just about any mental skill: facility with language, playing a musical instrument.
And, most importantly, anyone can acquire it at any age.
Can you tell someone it’s too late to learn, say, French? It all depends on shedding the “I’m not cut out for it” disposition and committing to practice.
There is world of elegance and beauty in math after crossing a threshold of skill level, just as with a musical instrument.
Let’s say a bit more about practice: You surely know a musical instrument cannot be learned merely by watching videos or reading about it. Proficiency requires regular and intense practice. The best part of practice is that, even though progress is not instantaneous, you can see results after a while.
Another advantage: the nature of practice is that many people give up. So, if you don’t, you are ahead of those that do.
Finally, the connection between programming and math:
- Many programmers do not use advanced math. But if you add a bit of math, you can do many interesting things in programming, as anyone who deals with data will tell you.
Some aspects of computer science that have a strong mathematical underpinning are just … a lot of fun!
End-Of-Module Problems
Full credit is 100 pts. There is no extra credit.
Problem 1.0.1 (40 pts)
Write a function rangelike that takes an integer argument and returns an ordered list of integers from 0 through one less than the integer argument. If the argument is less than or equal to 0, the function should return an empty list.
Starter code:
def rangelike(limit):
output_list = []
# your code goes here
return output_list
Examples:
rangelike(5) should return list [0, 1, 2, 3, 4]rangelike(3) should return list [0, 1, 2]rangelike(-1) should return an empty list []
Submit as rangelike.py.
Problem 1.0.2 (40 pts)
Write a function remove_first that takes a list as its argument and returns that list with the first element removed. If the list was empty, it should return an empty list.
Starter code:
def remove_first(input_list):
output_list = []
# your code goes here
return output_list
Examples:
remove_first(['DC', 'Boston', 'NYC']) should return list ['Boston', 'NYC']remove_first([22, 31, 40, 8]) should return list [31, 40, 8]remove_first(["Element"]) should return an empty list []remove_first([]) should also return an empty list []
Submit as remove_first.py.
Problem 1.0.3 (40 pts)
Write a function left_rotate that implements the left rotation from Exercise 1.0.17 on an input list and returns the new list.
Every element of the list should move ‘left,’ except for the first element, which moves to the last position. Input lists will always have length greater than one.
Starter code:
def left_rotate(input_list):
output_list = []
# your code goes here
return output_list
Example output:
left_rotate([0, 2, 4, 6]) should return [2, 4, 6, 0].left_rotate(['DC', 'Boston', 'NYC']) should return ['Boston', 'NYC', 'DC'].left_rotate(['duck', 'goose']) should return ['goose', 'duck'].
Submit as left_rotate_func.py.
Problem 1.0.4 (40 pts)
Write a function appendix that, given an input list, returns a new list that has the same elements as the original list, with one additional element, the integer 9.
Do this without modifying the input list.
Example output:
x = [1, 2, 4]
y = appendix(x)
print(x, y)
Should print [1, 2, 4] [1, 2, 4, 9]
x = ["nine"]
y = appendix(x)
print(x, y)
Should print ['nine'] ['nine', 9]
Submit as appendix.py.