Module 1.5 - Review

Objectives

The main goal of this module is to step back and review core concepts in programming: loops, conditionals, lists, functions.

1.5.0 Variables

Consider:

a = 3                
x = 3.14
s = 'hello'
immensely_pleased = False
odds = [1, 3, 5, 7]
x = 2.718
odds[2] = 9

Variables have four aspects to them:

• A name, like x or immensely_pleased above.
  • Variable names don’t change during execution, they are given by the programmer
• A current value.
  • At any moment during execution, a variable has a value. This value can change (often does) during execution.
• A scope. We’ll discuss this more in Unit 2.
• A type, such as integer, float, string, Boolean, list (and there are a few more, an advanced topic).

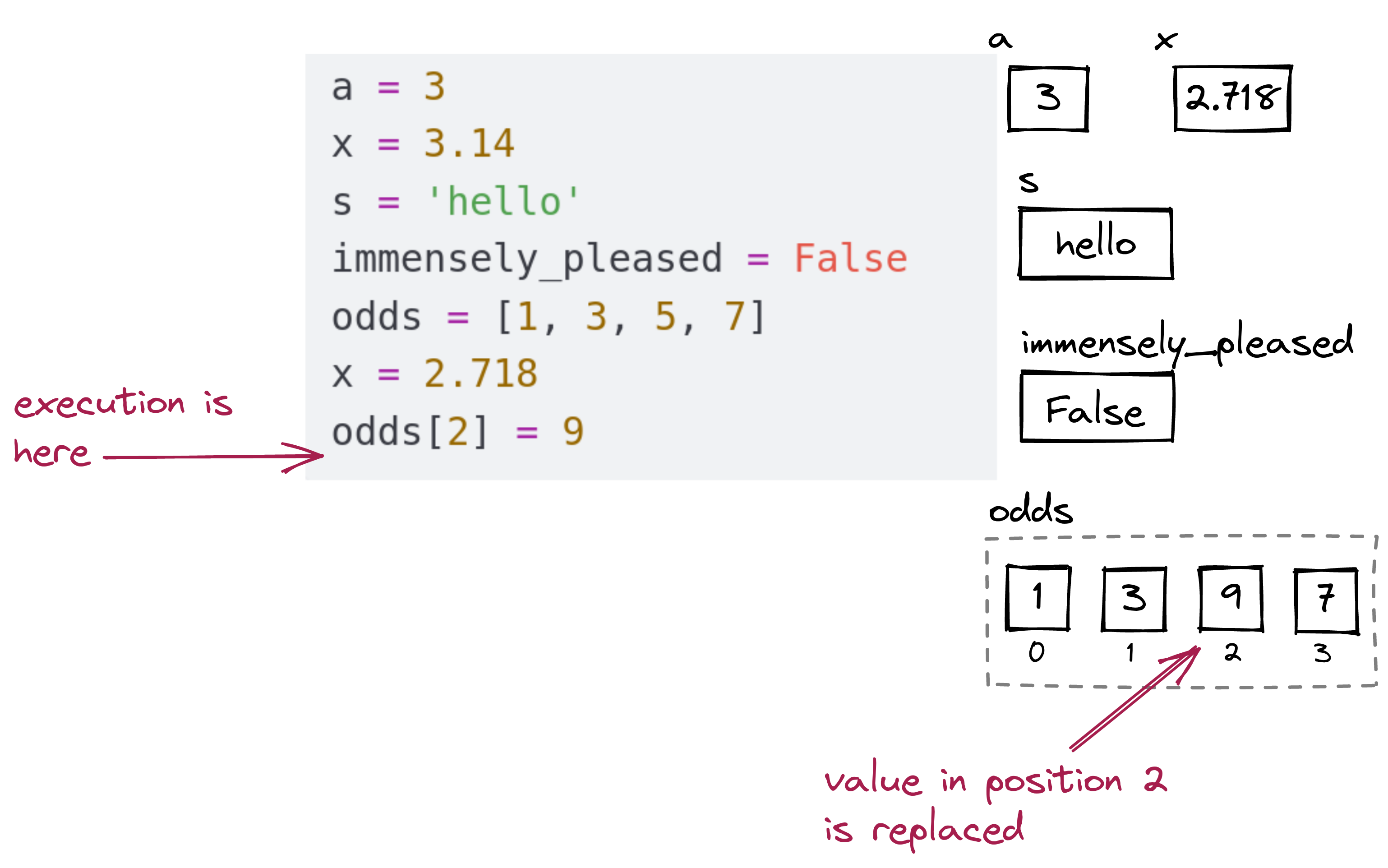
Let’s examine what happens when each line in the above program executes:

When the first line executes:

After the second line executes:

After the third line:

After the fourth:

After the fifth:

Then, one of the variables does have its value replaced:

Finally, one of the elements in the list gets replaced:

Now, there is a somewhat highly technical point to be made: - The “box” is what we’re using to conceptualize what a variable is, and how it behaves when we change it. - Generally, this is how you should think of it. - However, some books will present certain kinds of variables differently, with more detail. - Underneath the hood, in fact, string and list variables are a bit different.

So, for the sake of completeness, we’ll just point out this more detailed version:

Here:

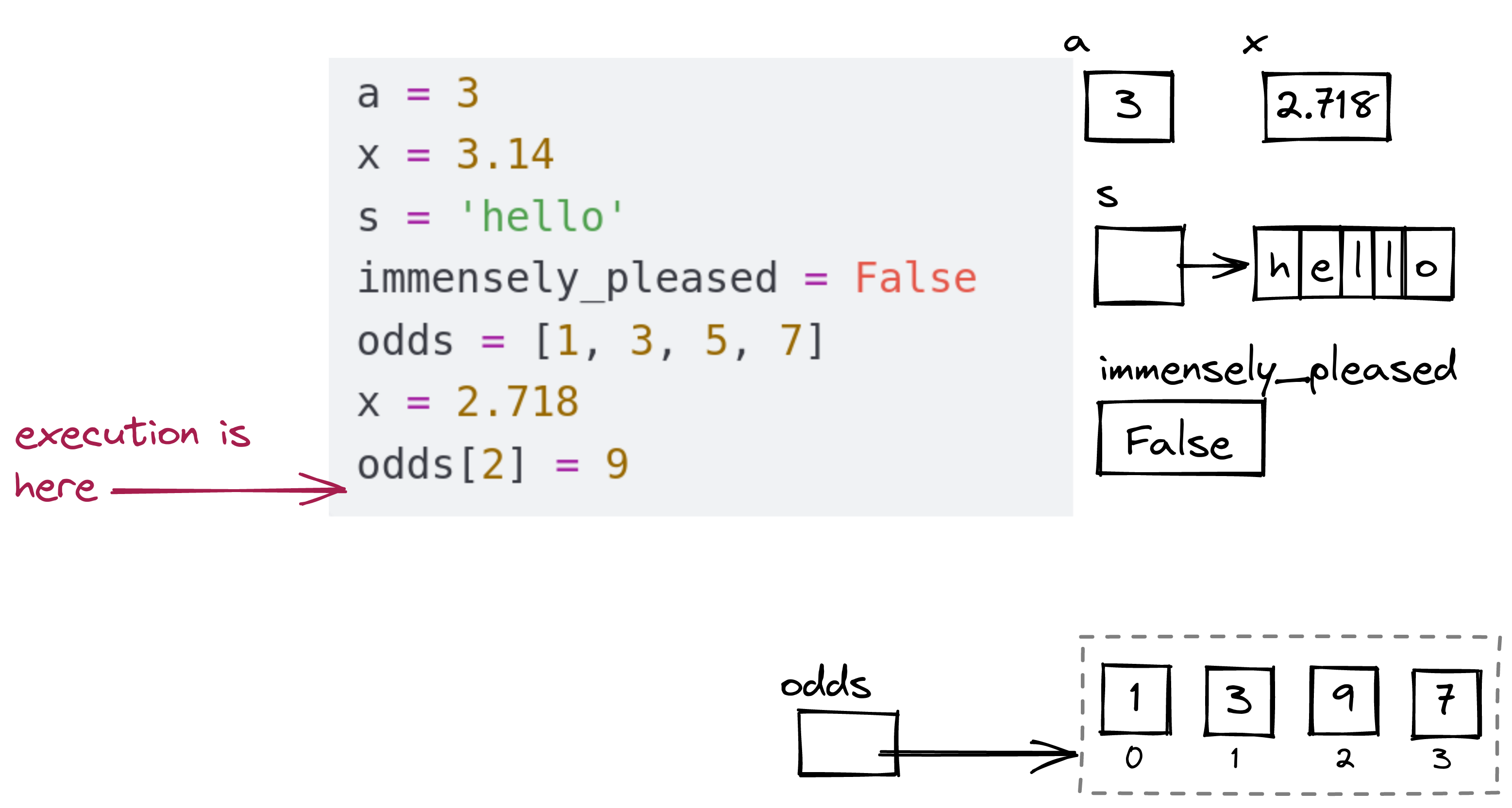
• String and list variables are themselves small boxes. These variables contain a reference (conceptualized by the black arrow above) to the actual data. The actual data for a string (the letters in it) are stored side by side, which is why we can “get at” letters via code like s[2] (3rd char in string).
  This more detailed version will make sense when you eventually get to see objects (a feature of Python) in the future.

1.5.1    How to Read and Mentally Execute Programs

Let’s start with a simple example:

x = 2
y = 3
x = x + y

for i in range(6):
    x = x + i

print('x =', x)

x = 20

Let’s look at this in steps:

First, start by noticing the chunks of code:

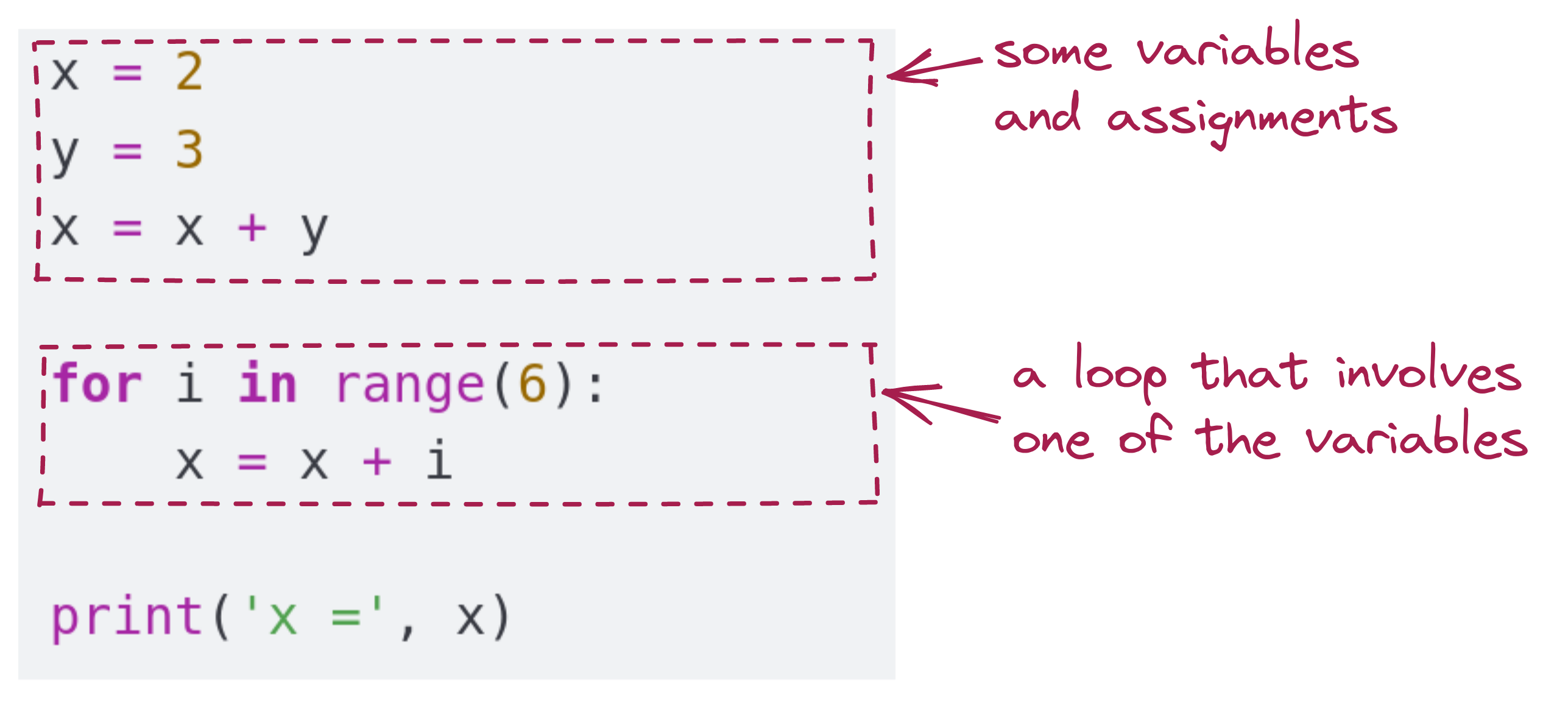
Next, walk through the execution of the first chunk, and notice that the value of x is what’s used later:

• If it helps to picture the boxes for x and y, then do so.
  • Look at the statement x = x + y and say to yourself: “First, let’s look at the right side, and the values of x and y now”.
  • Go backwards in the code to see the values of x and y.
  • Then perform the operation to get the new value of x (5, in this case) that replaces what was there (which was 2).
• Notice key aspects of the loop without yet executing iteration by iteration:

Then get down to the iterative level and execute iteration by iteration:

                           i      x
  Before loop starts:             5
  After first iteration    0      5
  After i is 1             1      6
  After i is 2             2      8
  After i is 3             3      11
  After i is 4             4      15
  After i is 5             5      20

Finally, there’s the print statement:

Exercise 1.5.1

Exercise 1.5.1

Examine and mentally execute the following:

i = 1
j = 4
A = [2, 4, 6, 8, 10, 12]

total = 0
for k in range(i, j+1):
    total = total + A[k]

print('total =', total)

Then confirm by writing in execution_practice.py .

---

Next, let’s look at reading a complex conditional:

age = 17
maximum_feasible_age = 120
voting_age = 18
berlin_age = 16
toronto_age = 19
washington_age = 21

if age >= maximum_feasible_age or age < 0:
    print('That age is not realistic.')
else:
    if age >= voting_age:
        print('This person can vote in the USA.')
        if age > toronto_age:
            print('This person can buy a beer in Toronto.')
            if age > washington_age:
                print('This person can buy a beer in Washington, DC.')
    elif age >= berlin_age:
        print('This person can buy a bottle of beer in Berlin.')
    else:
        print('This person is a minor.')

We’ll do this in steps, working from the “outside going in”:

• Start by noticing some variables and values being assigned, followed by a large nested conditional:

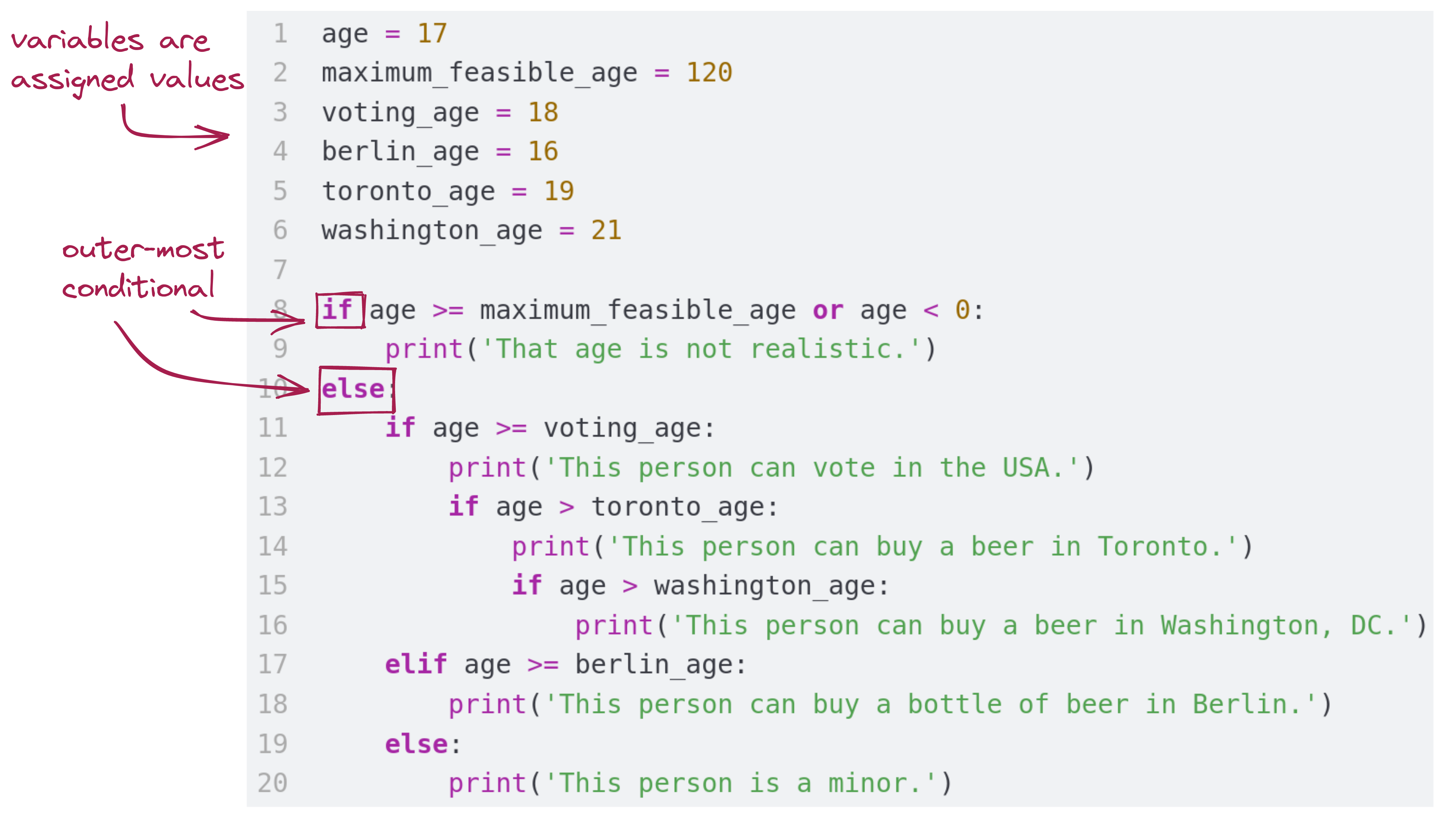
The conditions depend on the variables above.

• Next,identify which part of the outer conditional executes:

• The boolean expression maximum_feasible_age or age < 0 fails, so we move on to the else, which executes.

• Then, working inwards, we examine and see that the else statement’s code block is itself a big conditional:

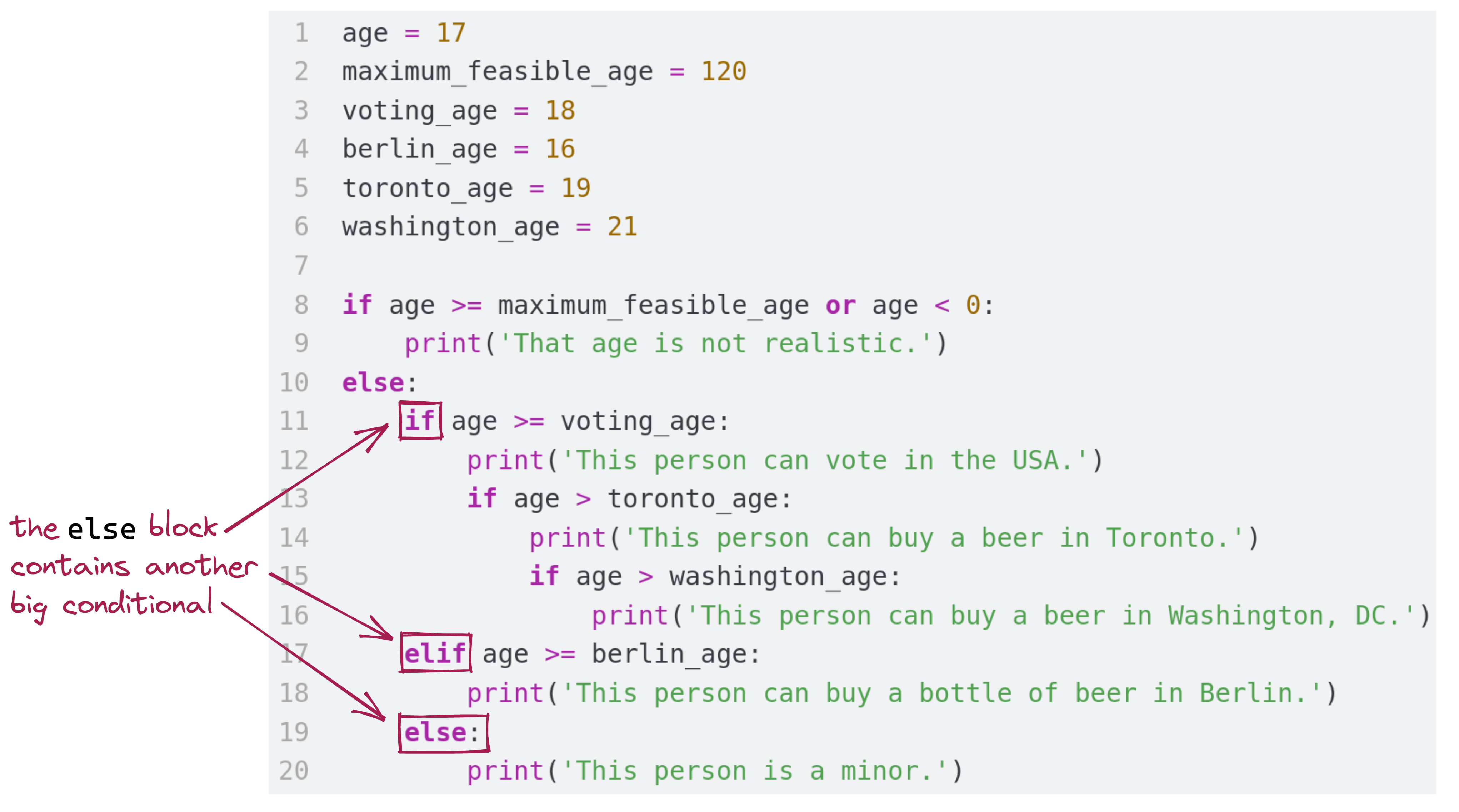
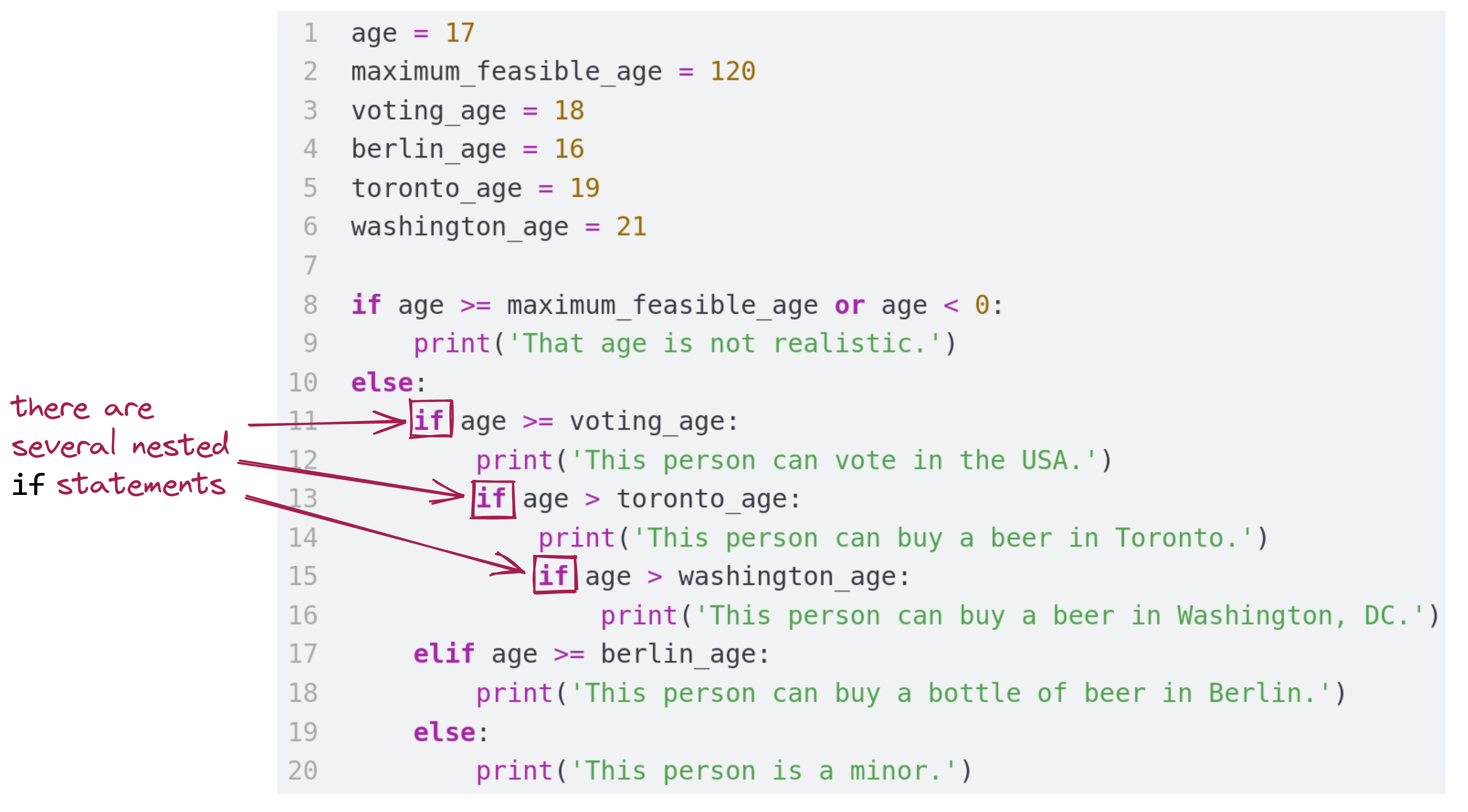
• The outer-most if condition fails (age >= voting_age is False) and so execution proceeds into the elif block: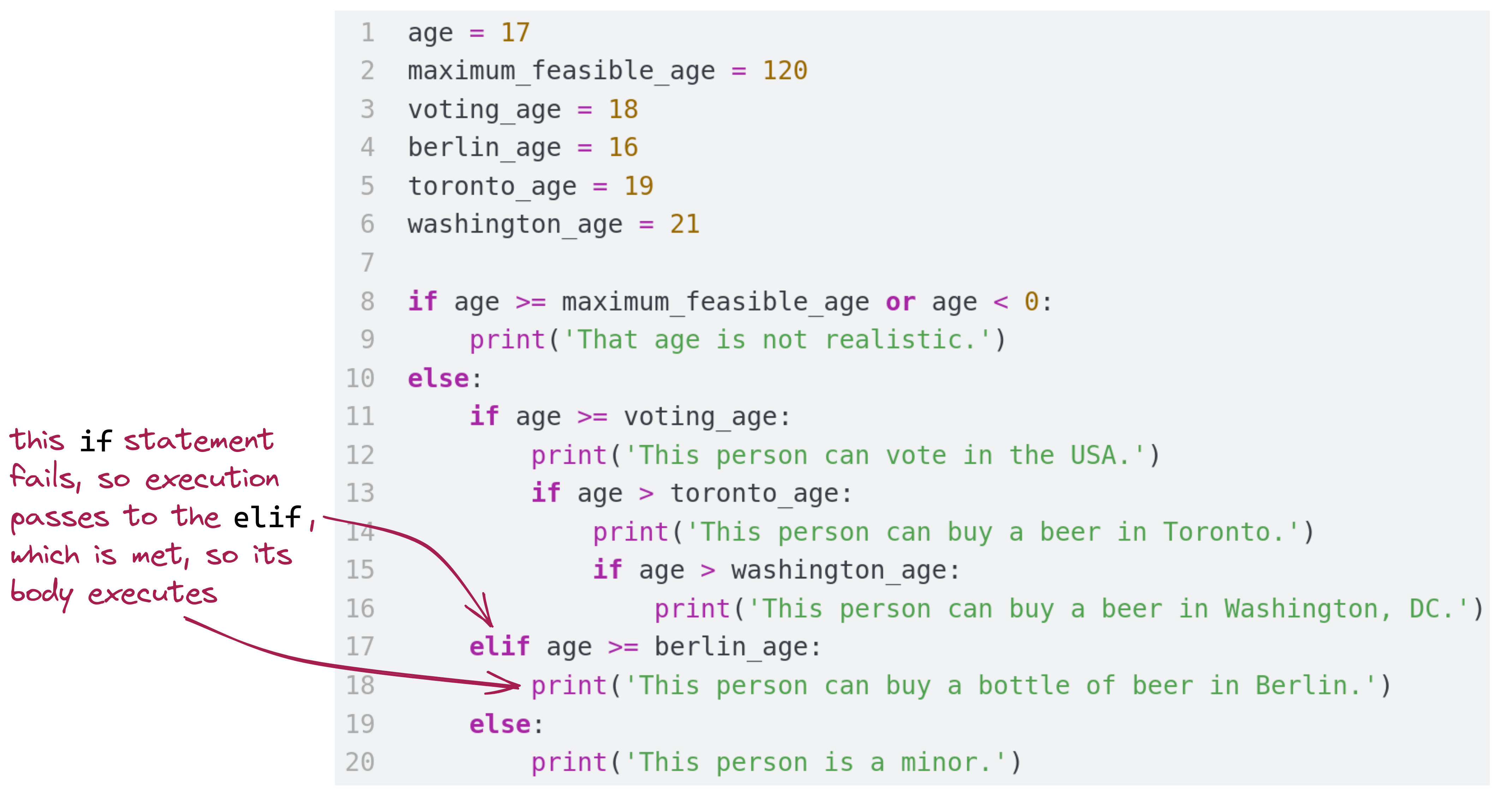

• The elif statement is True, and so its body (a print statement) executes

This example illustrates how critical it is to make sure the indentation is correct. For example, consider this variation:

Moving the indentation inward changes the logical execution of the series of conditionals.

Exercise 1.5.2

Exercise 1.5.2

Type up the above in execution_practice2.py. There are some logical errors with the set of conditionals: find them and fix them.

Hints:

• Someone who is 19 can vote in the USA and buy beer in Toronto and Berlin.
  
• Anyone under 18 is a minor.

Check your results with ages 15, 16, 17, 18, 19, 20, and 21.

Exercise 1.5.3

Exercise 1.5.3

As you’ve seen before, there’s often more than one way to solve any given problem.

In execution_practice3.py, rewrite the set of conditionals to work (give the same output for a given age) with no nested conditionals. You may use as many if, elif, and else statements as you need, but none may be nested.

Hint:

• The logical result of nested if statements can generally be produced, alternatively, using and and or in the condition of a single if statement.

As before, check your results with ages 15, 16, 17, 18, 19, 20, and 21.

Exercise 1.5.4

Exercise 1.5.4

Examine and mentally execute the following:

A = [-1, 2, 3, -5, 6, 7]

total = 0
for i in range(len(A)):
    if A[i] > 0:
        if A[i] % 2 == 0:
            total = total + A[i]
        else:
            print('rejected:', A[i])
    else:
        print('illegal:', A[i])

print(total)

Then confirm by writing in execution_practice4.py .

Exercise 1.5.5

Exercise 1.5.5

Consider the following program:

def printword(n):
    if n == 1:
        print('one')
    elif n == 2:
        print('two')
    elif n == 3:
        print('three')
    elif n == 4:
        print('four')
    else:
        print('cannot handle n > 4')

printword(1)
printword(2)
printword(3)
printword(4)
printword(5)

In conditional.py, rewrite the function so that it does the same thing but without using any elif statements.

1.5.2 Functions Without Parameters

Consider this example:

def print_two_xs():
    print('xx')

print('start')
print_two_xs()
print_two_xs()
print('end')

Let’s look at the execution step by step:

• First, Python reads through and stores the function definition:

• Then execution starts with the first print statement, followed by the first function call (or function invocation). At this point, execution enters the function:

• After the function executes, execution proceeds to just after the function call:

• In this particular case, the very next line is a call to the same function:

• After which:

Consider this program:

def print_two_xs():
    print('xx')

def print_three_ys():
    print('yyy')

def print_more():
    print_two_xs()
    print_three_ys()
    print('z')

print('start')
for i in range(8):
    if i % 3 == 0:
        print_two_xs()
    elif i % 3 == 1:
        print_three_ys()
    else:
        print_two_xs()
        print_three_ys()
    print_more()
print('end')

Exercise 1.5.6

Exercise 1.5.6

Examine and mentally execute the above program. Then confirm by writing it up in execution_practice5.py .

1.5.3   Functions With Parameters

Here’s an example:

def print_stuff(n):
    print('n =', n)
    n = 2*n
    print('twice n =', n)
    n = n // 4
    print('half n =', n)

m = 4
print(m)
print_stuff(m)
print(m)

• The parameter variable n gets its value from the argument variable:

• Recall that // is the integer division operator. Later in the function, the parameter variable gets its value changed:

It’s important to realize that we could have named the argument variable n as well:

Any code inside the function that uses or modifies n affects only the parameter variable n (the n inside the function and not the n outside the function).

Let’s emphasize one more thing by looking at:

def print_stuff(n):
    print('n =', n)
    n = 2*n
    print('twice n =', n)
    n = n // 4
    print('half n =', n) 
    print('m =', m)  # Trying to access m

m = 4
print(m)
print_stuff(m)
print(m) 
print('n =', n) # Trying to access n      

Exercise 1.5.7

Exercise 1.5.7

Type up the above in variable_access.py. Can you explain why half of the original n is calculated as n // 4?

You will notice that m is accessible in the function whereas the parameter variable n is not accessible outside. This is a topic (called scope) that we’ll address in Unit 2.

1.5.4 Functions That Return Values

Let’s look at an example:

def incr(n):
    m = n + 1
    return m

i = 5
j = incr(i)
k = incr( incr( incr(j) ) )
print(k)

• Consider the moment the first call to the incr() function occurs: j = incr(i)
• Here, the value in argument variable i is copied into parameter variable n: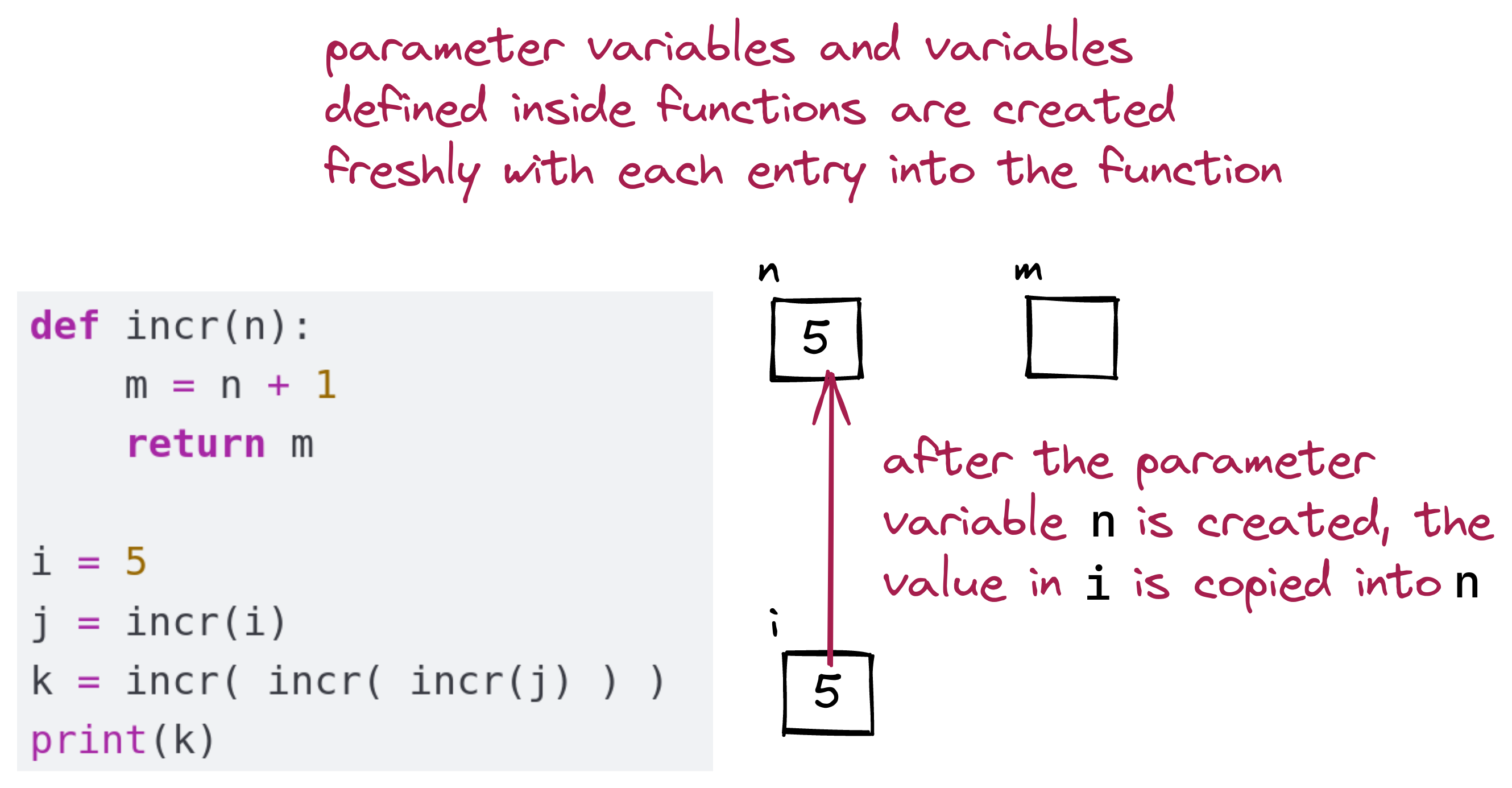

• Then, the value m becomes 6, which is returned when the return statement executes:

• Immediately afterward, the function call, complete, is effectively replaced by the return value:

• After the return occurs, remember that the parameter and other function-defined variables disappear. (Fresh versions will be created whenever another function call occurs.) Now let’s examine:

k = incr( incr( incr(j) ) )

• At this moment j has the value 6.
• The innermost call happens first: k = incr( incr( incr(j) ) ) which calls to incr() with argument 6, returning 7, which results in k = incr( incr(7) )
  
• k = incr( incr( 7 ) ) calls incr() with argument 7, which returns 8, which results in k = incr( 8 )
  
• Finally, k = incr( 8 ) similarly results in k = 9
  
• Lastly, remember that a return statement can have expressions. Which means we can shorten incr() to:

def incr(n):
    return n+1

• We could also place another function call in the return statement itself:

def incr(n):
    return n+1

def double_incr(n):
    return incr(incr(n))

This is a shorter way of writing

def incr(n):
    return n+1

def double_incr(n):
    k = incr(incr(n))
    return k

Consider a function with multiple returns:

def strange(n):
    print('start-of-strange')
    if n < 0:
        return 0
    elif n == 0:
        return 1
    else:
        s = 1
        for k in range(n+1):
            s = s + k
        return s
    print('end-of-strange')

print(strange(-3))
print(strange(0))
print(strange(3))

Note: In the first call to the function strange(), the parameter n will have the value -3. - In this case, we see ‘start-of-strange’ printed. The if condition is true, which means the first return executes:

def strange(n): 
    print('start-of-strange')
    if n < 0:
        return 0 # function returns here
    elif n == 0:
        return 1
    else:
        s = 1
        for k in range(n+1):
            s = s + k
        return s
    print('end-of-strange') 

• Execution leaves the function immediately, which means nothing else in the function executes.

Exercise 1.5.8

Exercise 1.5.8

For each of the three calls to the function strange(), can you tell whether ‘end-of-strange’ gets printed? Then confirm by typing it up in strange_example.py.

1.5.5    Lists Are Different

Consider

def add_one(n):
    n = n + 1
    print('incr: n=', n)

def list_add_one(A):
    for k in range(0, len(A)):
        A[k] = A[k] + 1
    print('list_incr: A=', A)

p = 3
add_one(p)
print(p)

B = [1, 2, 3]
list_add_one(B)
print(B)

Exercise 1.5.9

Exercise 1.5.9

Type up the above in list_example.py .

• The add_one() function has no effect on the variable p, since the value in p gets copied into n. The parameter variable n does get 1 added (as the print in add_one() confirms.
• On the other hand, print(B) shows that the elements of B have 1 added to each of them.
• Why is this? Why are lists different as parameters?
  
• List variables are actually references, sometimes called pointers.
• Think of a reference or pointer as a special token that provides access to the list elements.
• Whoever has the token can access the list elements.
• When the contents of variable B’s are copied into parameter variable A, then the variable A has the special token.
• Which means variable A access the list elements and can change those.
  
• Why was the Python language designed this way? Copying over big lists into parameter variables can greatly slow down execution.
• Therefore, lists (and other such complex objects) don’t have their elements copied.
• Instead, it’s only the reference (which is really a number, under the hood) gets copied.
  For practice, let’s look at a list example with Boolean values (True, False):

def list_or(A):
    x = True
    for k in range(0, len(A)):
        x = x or (not A[k])
    return x

B = [True, True, False, False]
print(list_or(B))

Exercise 1.5.10

Exercise 1.5.10

Trace through each iteration of the loop in the function list_or(), showing x, k, and each A[k]. Then confirm in list_example2.py.

And another example for practice:

def within1(x, y):
    # Write your code here to return True or False
    # Return True if the difference between x and y is 1 or less

def first_diff(A, B):
    k = 0
    while (k < len(A)) and (within1(A[k], B[k])):
        k = k + 1
    if k == len(A):
        return -1
    else:
        return k

X = [1, 2, 3, 4]
Y = [2, 2, 3, 3]
Z = [1, 1, 1, 4]
print(first_diff(X,Y))    # Should print -1
print(first_diff(X,Z))    # Should print 2

Exercise 1.5.11

Exercise 1.5.11

The function first_diff() is intended to take two lists, compare elements in the same positions, and identify the first position where the two lists differ by more than 1. If no such difference exists, the function should return -1.

In list_example3.py, complete the code in the within1() function so that it returns True only when the difference between x and y is 1 or less, i.e. True when x=1and y=2, or when x=4 and y=3, or when x=5 and y=5. After that, trace through the iteration in the while-loop.

1.5.6    Why Are Functions Useful?

Functions are very useful for four different reasons:

Code written in a function can be re-used. For example, compare:

X = [1, 3, 5, 7]
total = 0
for k in X:
    total += k
avg = total / len(X)
print(avg)

Y = [2, 4, 6, 8, 10]
total = 0
for k in Y:
    total += k
avg = total / len(Y)
print(avg)

with

def mean(A):
    total = 0
    for k in A:
        total += k
    return total / len(A)

X = [1, 3, 5, 7]
print(mean(X))
Y = [2, 4, 6, 8, 10]
print(mean(Y))

The second reason is, as this example shows:

z = incr( diff(x, y) )

(You can imagine what the functions incr() and diff() do.) Another example showing compactness with functions:

s = '  hello  '
print(len(s.strip()))

A long program broken up into functions will make the program more readable and therefore more easily understood. The biggest reason, perhaps, is that it has become one of two important ways by which multiple programmers use each others’ code.

As an example, you have used functions in drawtool and Python functions like math.random().

How do you know when to create functions vs. writing long code? There are no rules. The judgement comes with practice. Generally, tiny computations like increment don’t need functions. Any significant computation that is likely to be re-used should probably be in a function. Also, use functions when when doing so improves readability.

End-Of-Module Problems

Full credit is 100 pts. There is no extra credit.

Problem 1.5.1 (30 pts)

Problem 1.5.1 (30 pts)

Write a function list_max that takes one argument, a list. The list will contain numbers (ints and floats). Your function should return the biggest number in the list.

Write another function list_min that takes one argument, a list. The list will contain numbers (ints and floats). Your function should return the smallest number in the list.

Do not use built-in min or max functions (or any libraries).

Submit both functions in one file, list_min_max.py.

Problem 1.5.2 (30 pts)

Problem 1.5.2 (30 pts)

Write a function list_remove that takes two arguments: the first argument is a list, the second argument could be anything.

• If the second argument is in the input list, return a list identical to the input list except with the first instance of the second argument removed.
• If the second argument is not in the input list, simply return the list.

Do not use the built-in .remove function (or any other function that removes elements from a list).

Examples:

• list_remove([3, 4, 7], 7) returns [3, 4].
• list_remove([3, 4, 7], 8) returns [3, 4, 7].
• list_remove(['A', 'B', 'B', 'A'], 'A') returns ['B', 'B', 'A'].

Submit as list_remove.py.

Problem 1.5.3 (30 pts)

Problem 1.5.3 (30 pts)

Write a function string_count that takes two arguments, both are strings.

• Count how many times the second string appears in the first string.
• Return that count.

Do not use the built-in .count function or the built-in .find function.

Examples:

• string_count('verbatim', 'r') should return 1.
• string_count('Mississippi', 's') should return 4.
• string_count('After the storm passed, they sailed.', 'the') should return 2.

Submit as string_count.py.

Problem 1.5.4 (30 pts)

Problem 1.5.4 (30 pts)

Write a function string_strip that takes as input a string and removes space ' ' and newline '\n' characters from the beginning and the end of the string, to whatever extent consecutive instances of either character exist. (You cannot actually modify a string, but your function should return a new string with this operation effectively performed.)

Examples:

• string_strip(" \n great! ") returns string "great!".
• string_strip("ok ") returns string "ok".
• string_strip(" \n what's next?\n \n") returns string "what's next?".

Submit as string_strip.py. Do not use the built-in .strip function.

Problem 1.5.5 (30 pts)

Problem 1.5.5 (30 pts)

Write a function string_split that takes takes two arguments, both strings. The function should “split” the first string on the second string, and return a list of the substrings, identical to the .split function.

Examples:

• string_split('everything rings falser, a little metallic', ' ') returns ['everything', 'rings', 'falser,', 'a', 'little', 'metallic']
• string_split('the finer things', 'er') returns ['the fin', ' things']
• string_split('the finer things', 'the') returns ['', ' finer things']

Submit as string_split.py. Do not use the built-in .split function.