a = 3
b = 4
c = 5
if a < b:
if a < c:
print('a is the smallest')
else:
print('a is not the smallest')
print('Done')a is the smallest
DoneBy the end of this module you will be able to:
if, if-else, and if-elif-else statements.In Module 0.4, we learned how to use if, elif, and else statements to conditionally execute code based on the values of different variables. Review that module now - what we learn here will build on it.
Remember:
if statement evaluates an expression, and if that expression is true, the indented code block after it will run.if statement is not true, any elif statements will be evaluated in order.
elif statement is true, the indented code block after it will run.elif statement is not true, the next elif (if there is one) will be evaluated.if or elif statements are true, if there is an else statement, its indented code block will run.There must be an if, there may be any number (including 0) elif statements, and there may be one or zero else statements.
Consider this program:
a = 3
b = 4
c = 5
if a < b:
if a < c:
print('a is the smallest')
else:
print('a is not the smallest')
print('Done')a is the smallest
DoneThis is an example of a nested conditional (nested if).
Examine the indented structure:
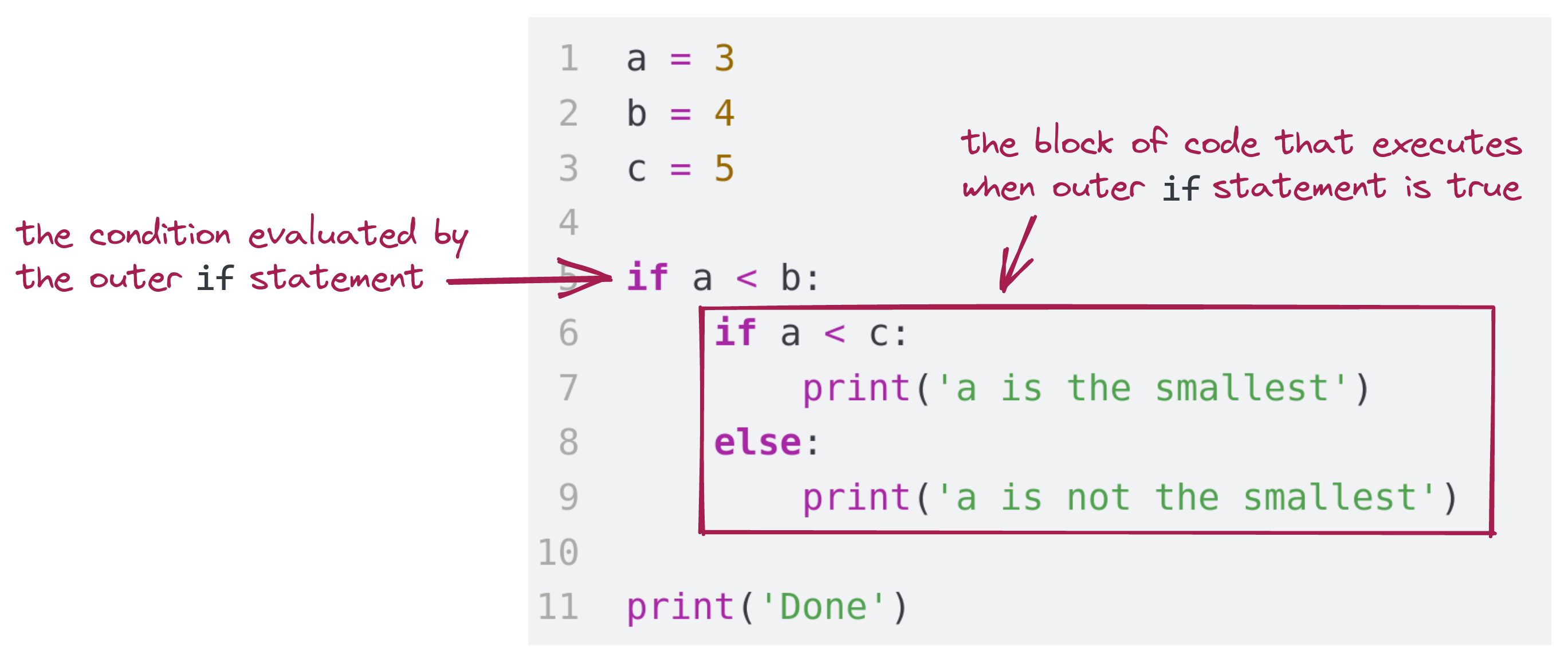
The execution pathway, illustrated:

The execution pathway, described:
if statement on Line 5 is true, so the outer if body begins executing on Line 6if statement on Line 6 is true, so the inner if body on Line 7 executeselse on Line 8 does not result in execution because the associated if (on Line 6) was true, so Line 9 is skippedif statement, the program is still inside the body of the outer if statement, but there is no more code, so the program exits the conditional block and executes Line 14.Consider this variation:
a = 3
b = 4
c = 5
if a < b:
if a < c:
print('a is the smallest')
else:
print('a is not the smallest')
print('We know a is less than b')
else:
print('We know a is not less than b')
print('Done')a is the smallest
We know a is less than b
DoneType up the above in nestedif.py. Draw (or desribe with line numbers) the flow of execution for the following three cases:
a=3, b=4, c=5a=3, b=4, c=2a=6, b=4, c=5In smallest_of_three.py, modify the above program so that it prints out, appropriately, one of a is the smallest, b is the smallest or c is the smallest, depending on the actual values of a, b, and c. Try different values of these variables to make sure your program is working correctly.
A numeric variable can be: strictly less, less than or equal to, strictly greater, greater than or equal to, or equal to another variable. Accordingly, the different types of less/greater comparisons are:
Consider this program:
== operator: Because we’ve been using the = (single equals) operator for assigning values to variables, we need something else to test for equality.== as in: if x == y:= and == is very important to remember. It’s easy to confuse the two.if statement combines two conditions: if x == y and y == z:andThe two parts are often called clauses:
(x == y)(y == z)The and operator works like this:
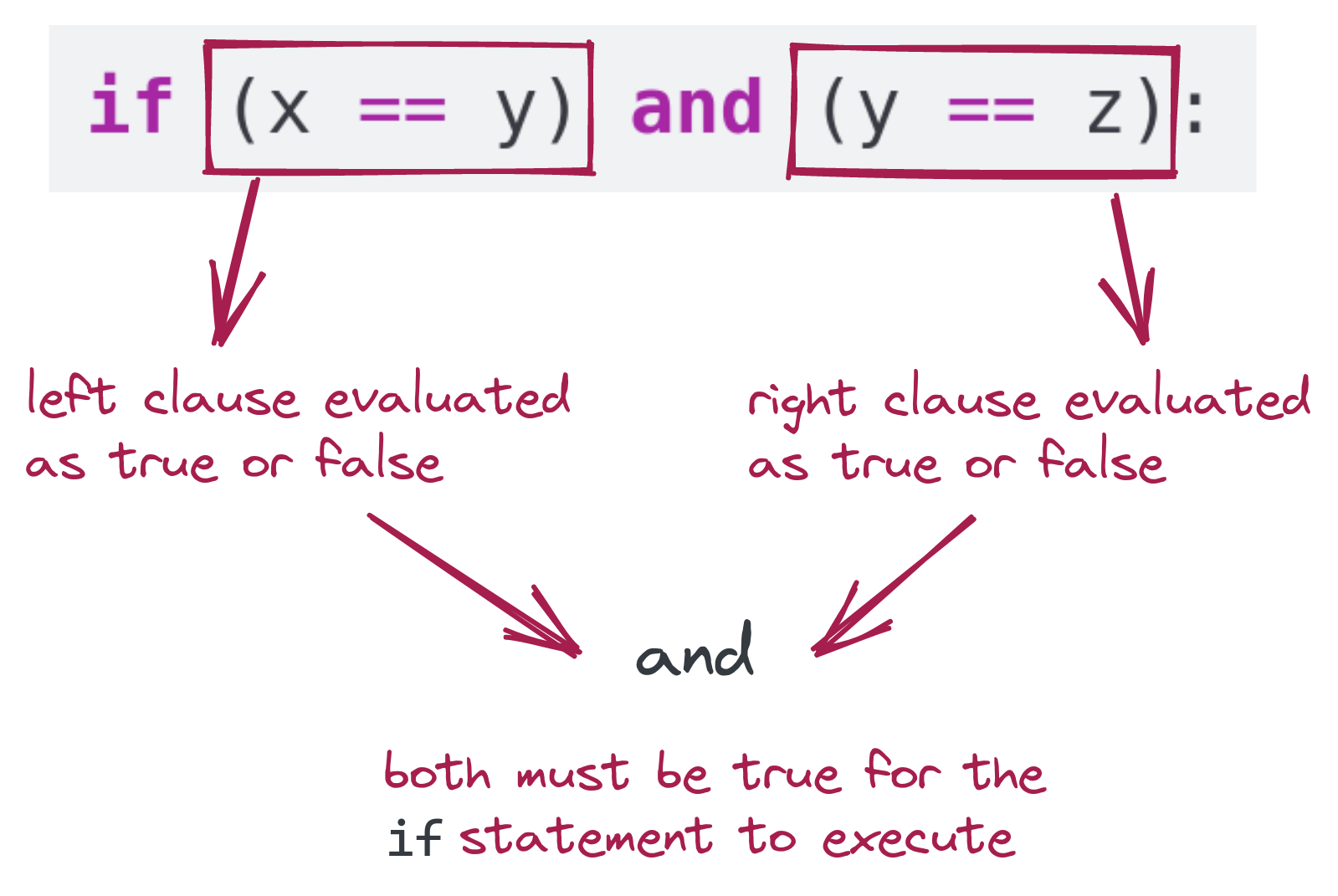
Boolean is pronounced “BOO lee unn”. - A Boolean operator takes expressions and computes to either true or false.
Let’s go back to finding the smallest of three numbers using conditionals:
In smallest_of_three2.py, fill in code to identify which of the three variables has the smallest value, depending on the actual values of a, b, and c. Use if statements with multiple clauses. Try different values of these variables to make sure your program is working correctly.
Your printed output should take the form: x is smallest (where x is replaced by a,b, or c, depending on their values)
As the counterpart to the and operator, there is the or operator:
Type up the above in boolean2.py. Then try a = 0.5.
We have shown how to write “less than or equal to” using <= . So, now we can add “equals” and “not equals” to the numeric comparisons:
a < b # Strictly less than
a <= b # Less than or equal to
a > b # Strictly greater than
a >= b # Greater than or equal to
a == b # Exactly equal
a != b # Not equalFor the or operator to evaluate to true, at least one of the two expressions must be true. Both being true satisfies this as wel.
Consider:
print statement executes.print statement will execute.print statement will execute. But if a=11, b=12, the or fails (both clauses are false), and the print won’t execute. Incidentally, let’s replace or with and in the above case, and see what we get:In this case, both sub-conditions are satisfied, and so the whole if condition is satisfied, which means the print will execute. But if we change the value of b:
a = 3
b = 11 # we changed the value for b
if (a < 10) and (b < 10):
print('Both of them are less than 10')In this case, the second comparison fails, and the print won’t occur. Whereas if we change the and to an or:
a = 3
b = 11
if (a < 10) or (b < 10): # we changed the and to an or
print('One or both of them is less than 10') Here, it’s enough that a is less than 10, and so the print executes even though “b less than 10” fails.
Next, let’s look at the “not equals” operator, written != :
Type up the above in boolean3.py, then change z to be 6 (the same as y). What do you observe?
One can combine any number of and statements. For example:
We should read != as “not equals” just as we read == as “equals”.
There is another operator called not, which applies to Boolean expressions. One can apply the not operator to groups of clauses using additional parentheses:
Here, not reverses the True or False value of whatever it applies to:
not True is Falsenot False is Truea is equal to 5, a > 4 is True, so not (a > 4) is FalseConsider the expression if not ((x == 5) or (x == 6)):
x is 8. So, neither (x == 5) nor (x == 6) evaluates to True.( (x == 5) or (x ==6) ) is False.not ( (x == 5) or (x ==6) ) to evaluate to True.Most logical expressions can be evaluated in more than one way. For instance, a > 4 is the same as not (a <= 4). Similarly, a != 5 is the same as not (a = 5).
This means there is often no single “correct” way to represent a logical expression. Take care, and make good use of parentheses: logical expressions should be both:
Suppose integer variables a,b,c,d,e have values a=1, b=1, c=3, d=4, e=5. Consider the following three expressions:
( (a <= b) and (c+d > e) and (d > 1) )
( (a > c) or ( (c+1 < e) and (c-b > a) ) )
not ( (b == d-c) and (a > b) or (c < d) )Try to evaluate each expression by hand. Then, in boolean4.py, write up each of these in an if statement to see if the result matches with your hand-evaluation.
Let’s write a program to loop through integers and print only the even numbers:
In oddeven.py, modify the above program so that for every number between n and 1, going backwards, the program prints whether it’s even or odd, as in:
10 is even
9 is odd
8 is even
7 is odd
6 is even
5 is odd
4 is even
3 is odd
2 is even
1 is oddSuppose we have a list of numbers, representing daily profits (sometimes negative, sometimes positive) and we only want to add up the positive numbers:
earnings = [-5, 2, 3, -9, 12, 4, -30]
total = 0
for k in earnings:
if k >= 0:
total += k
print('Total profit =', total)Trace through the values of total and k.
Write up the above as total_profit.py and verify the trace.
Given a list like
we see that 12,13 and -21,-20 are pairs of consecutive numbers. Write a program called consecutive.py, with loop and a conditional to identify such consecutive pairs and print them. For the above list, the output should be:
Consecutive pair found: 12 13
Consecutive pair found: -21 -20Next, let’s write a program that asks the user to enter a number that we then check is in a list of numbers:
# The list of numbers:
A = [-5, 2, 4, -9, 12, 13, -30]
# Receive what the user types in (as a string):
user_str = input('Enter an integer: ')
# Convert string to integer:
k = int(user_str)
# Check whether in the list:
if k in A:
print(k,'is in the list')
else:
print(k,'is not in the list')Note: The in operator checks if a value is in a list:
k in A is True if k is one of the values in the list Aif k in A: runs if k is in ASuppose you are given two lists:
Notice that some elements of A (like 2) also exist in B. In twolist.py, use the list membership idea to print those elements of A that are also in B. For the above example, the output should be:
2 in A also found in B
-9 in A also found in B
13 in A also found in BConsider the following program that aims to find duplicates in a list:
in context
Be careful! The in keyword behaves differently in different contexts:
for k in A:, the in keyword tells Python to loop through the different members of Aif k in A, the in keyword checks if values are members of AThe key distinction is that the for loop declaration changes how in behaves. The in operator checks for membership, except when it is used in a for loop.
In the list, we can see that 2 occurs three times, and 3 occurs twice. Both should be listed as duplicates. Is this the case?
Trace through the iterations in the above program and explain why the above does not work.
Now consider this variation:
Trace through the iterations in the above program and explain the output. Why does the inner loop start with i+1?
Let’s now apply our practice with conditionals to solve some problems in probability and statistics.
For example: Suppose I toss a coin 4 times and observe the face that’s up. What is the probability that I get all “tails” (no toss shows “heads”).
Let’s do this in steps.
First, let’s write a program to toss a coin 4 times
Type up the above in cointosses.py and run it a few times to see what you get.
Note: We have made a list of strings:
Python has a useful way to randomly select a member of a list:
Alternatively, we could have written:
and avoided defining coin.
Next, instead of printing the results, let’s count the number of heads observed:
Type up the above in cointosses2.py and run it a few times to see what you get.
Observe how the string that’s randomly selected from the list is compared against ‘heads’:
Next, what we need to do is repeat the 4-coin toss many times: - Suppose we call each set of 4 coin tosses a single trial . - If we ran a single trial and obtained 1 heads and 3 tails (count=1), could we make a conclusion about the probability of getting 4 tails? No. - What we need to do is run a large number of trials and record in how many trials we get a run of 4 tails. We’ll use the term “success” to identify a trial in which we get all 4tails. Let’s examine the code:
import random
trials = 10
successes = 0
for i in range(trials):
# Count number of heads in 4 tosses:
count = 0
for i in range(4):
toss = random.choice(['heads', 'tails'])
if toss == 'heads':
count = count + 1
# If the count is zero, that's a success
if count == 0:
successes += 1
# Ratio of successes to trials:
probability = successes / trials
print('probability =', probability)Type up the above in cointosses3.py and run it a few times to see what you get. Then increase the number of trials to 100000 and see. The theoretical answer is 0.0625 (approximately 6% chance there’s no heads in 4 tosses).
The closed-form solution treats each coin toss as independent, with a probability of giving tails equal to \(\frac{1}{2}\).
The probability of four tails is given by multiplying the independent probabilities of each toss: \(\frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{2^4} = \frac{1}{16}\)
This must be multiplied by the number of ways to get four tails (there is only one way): \(\frac{1}{16} \cdot 1 = \frac{1}{16} = 0.0625\)
In cointosses4.py, write a program to run 100000 trials of the following experiment: toss a coin 10 times and record a success if you get an equal number of heads and tails.
Start with the following code:
Now let’s solve a problem with another random process: dice.
We’ll roll two 6-sided dice and add the numbers face up. We want to ask: what is the probability that we get 7 (when the faces are added)?
Here’s the program:
Type up the above in dice.py to see the result. Is there a sum of rolls that yields a higher probability than seven?
Let’s also look at how one can get Python to randomly generate real numbers:
import random
trials = 50
total = 0
for i in range(trials):
x = random.uniform(5, 10)
print(x)
total += x
print('mean =', total/trials)Note: By using x = random. uniform(5, 10) we can generate a random real number between 5 and 10, equally likely to take on any value between 5 and 10.
Type up the above in uniform.py, then increase the number of trials until the average “stabilizes” such that the average does not change by more than a small value, say 0.01, if you increase the trials further.
You can use programming to explore ideas in probability and statistics, and solve real problems as well. - These methods can be used to simulate a variety of real-world problems to get insight on how they work.
Let’s now use what we’ve learned to explore the notion of how computers can be programmed to generate abstract art.
In our first example, we’ll draw lines from one border of a square to another:
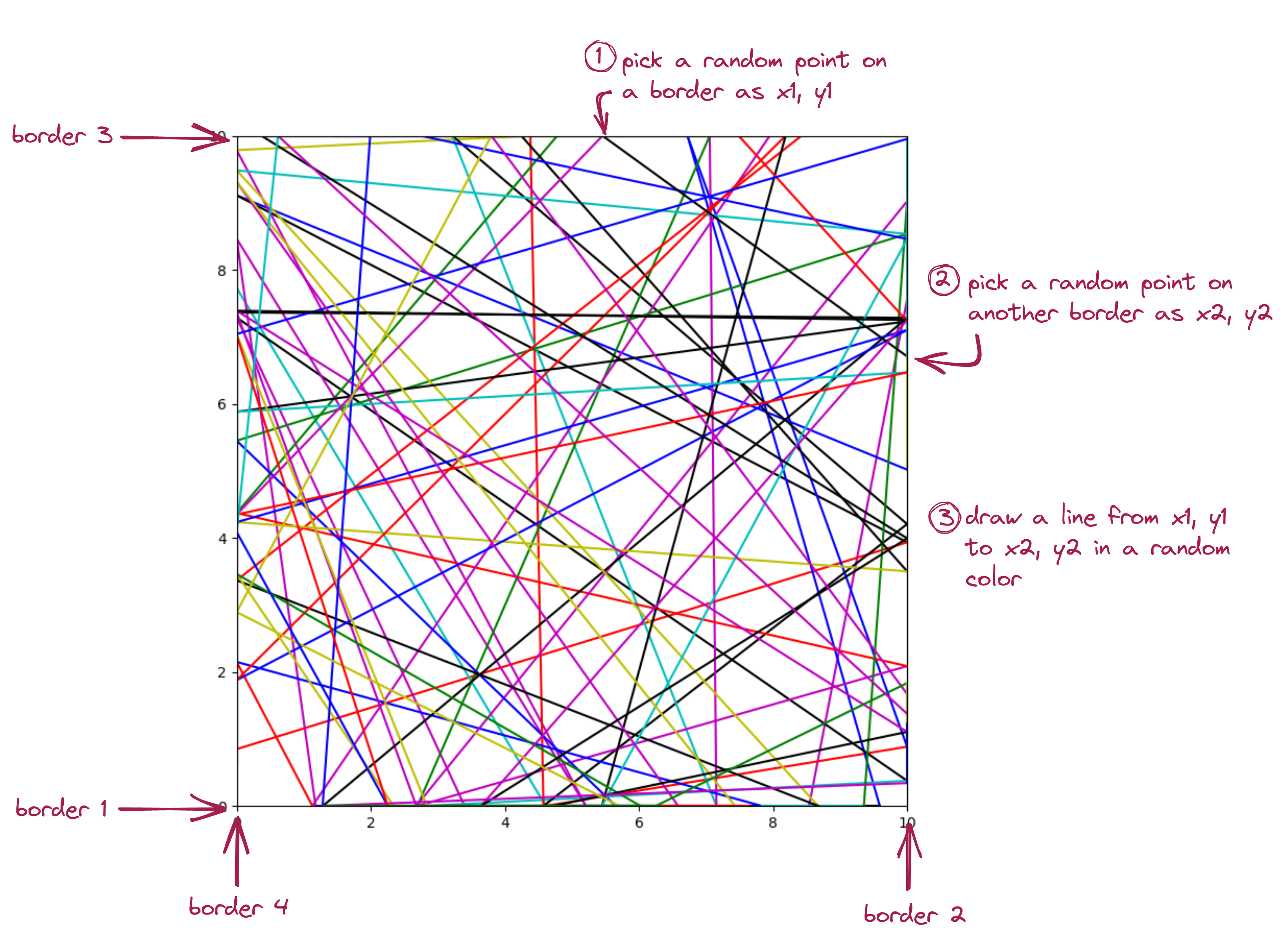
Let’s describe the main idea via some pseudocode:
In a loop we’ll generate:
Set up an initial x1,y1 and x2,y2
for i in ...
Pick a random color
Draw a line from x1,y1, y2,y2
Make the current endpoint the start of the next line:
x1 = x2
y1 = y2
Pick a random border
Now pick a new random point on the next borderDownload conditional_art.py and drawtool.py.
Try it out and then examine the code to confirm that it follows the pseudocode. Try different values of n. Can you change the choices of randomly chosen colors to improve the result? Does it look good with just two colors?
Contrast this method with modern neural network-based art generation tools, such as DALL-E, Stable Diffusion, or Midjourney. If you cannot access one of these, feel free to use examples from a recent article in the press.
Modern art generators like the ones listed above will generate images from text that you provide. It is possible that these generated images contain disturbing content. Choose your text prompts with care.
Are there any advantages to using a procedural method, such as the one we have written in Python, over a neural network-based probabalistic method such as those used in DALL-E, Stable Diffusion, or Midjourney?
Next, we’ll explore changes to generative art:
Download conditional_art2.py. Try out different values (between 0 and 1) of the structure parameter (on line 19 of conditional_art2.py), for example 0.9 and 1.1.
Is there a value that provides a mix you prefer? Try different values of n.
In each of the exercises below, first try to identify the error just by reading. Then type up the program to confirm, and after that, fix the error.
Full credit is 100 pts. There is no extra credit.
Write a function consecutive_finder that takes as input a list of integers and returns:
Examples:
consecutive_finder([0, 2, 4, 6]) would return 0.consecutive_finder([2, 4, 6, 8, 9]) would return 1.consecutive_finder([4, 3, 7]) would return 0.Submit as consecutive_finder.py
Write a function subset_selector that takes as input a list of integers and returns a new list, consisting of every member of the original list that satisfies all of:
For this problem, 0 is not divisible by three.
Examples:
subset_selector([1, 2, 3, 4]) returns [3].subset_selector([-5, -600, 0, -8, 25, 27, 2700]) returns [-8, 27].subset_selector([-10, 10, 11, -11, 12, 13]) returns [-10, 12].Submit as subset_selector.py.
Write a function fizzbuzz that takes as input any positive integer and returns:
'fizz' if the integer is evenly divisible by 3 and not 5'buzz' if the integer is evenly divisible by 5 and not 3'fizz buzz' if the integer is evenly divisible by 15Example output:
Should print: 1 2 fizz 4 buzz fizz 7 8 fizz buzz 11 fizz 13 14 fizz buzz 16 17 fizz 19
Submit as fizzbuzz_func.py.