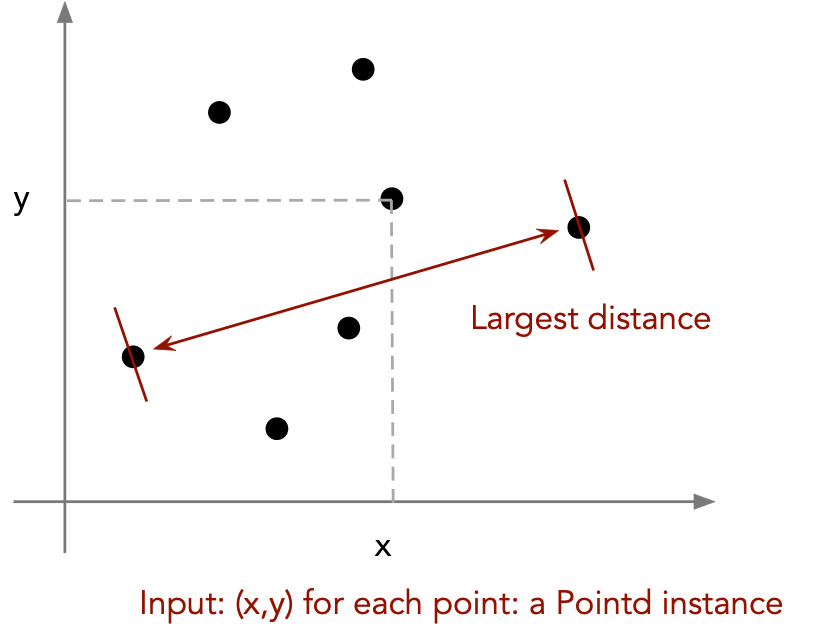
Consider the largest distance problem:

In-Class Exercise 1:
In this exercise you will write code to find the distance
between the two furthest points among a set of points:
Note: do not read any further until you solve this problem. (Yes,
there is a solution described below, but please develop your own.)
% java LargestDistance 50
public class Pointd {
public double x, y;
}
to hold the x and y coordinates of a point.
Now consider this algorithm:
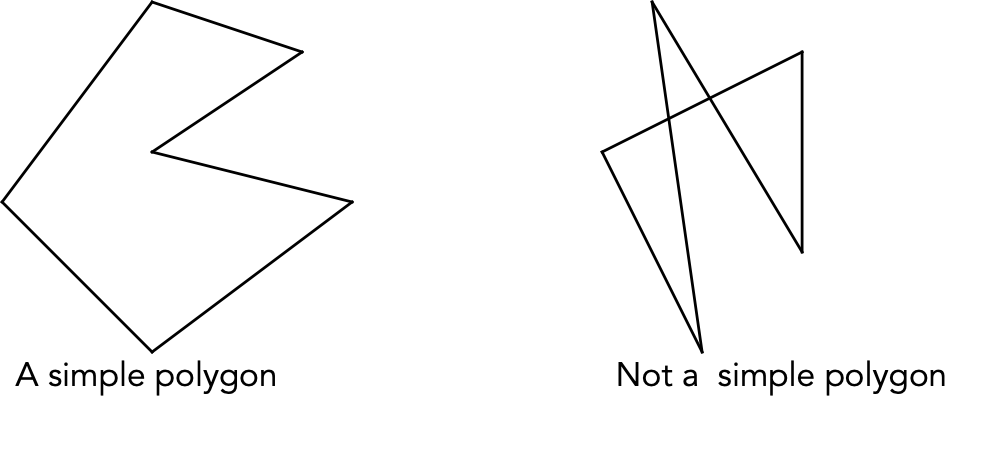
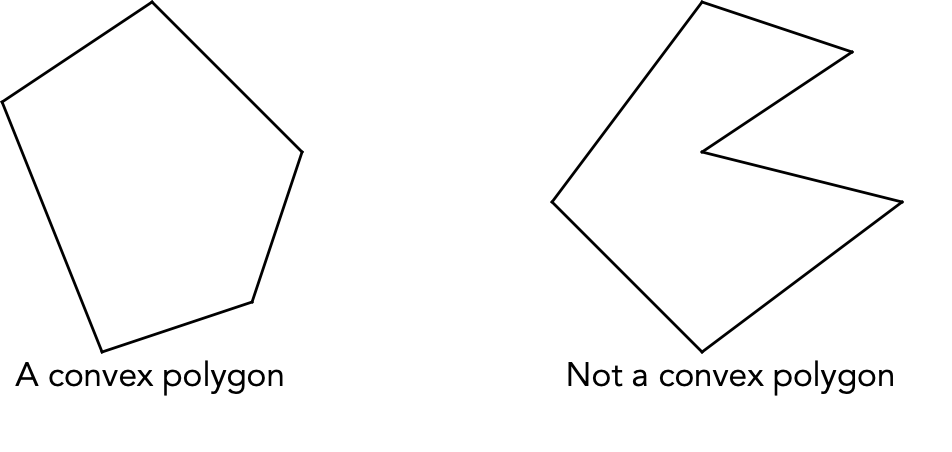
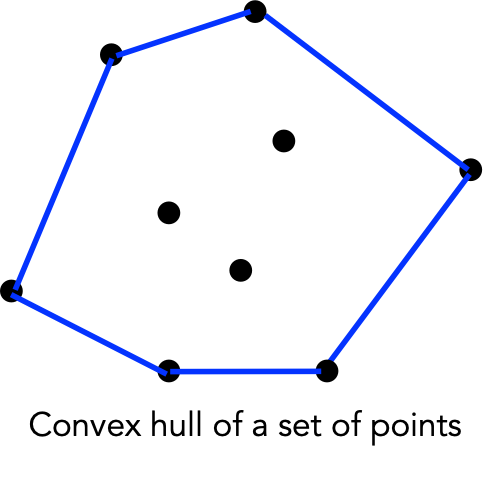
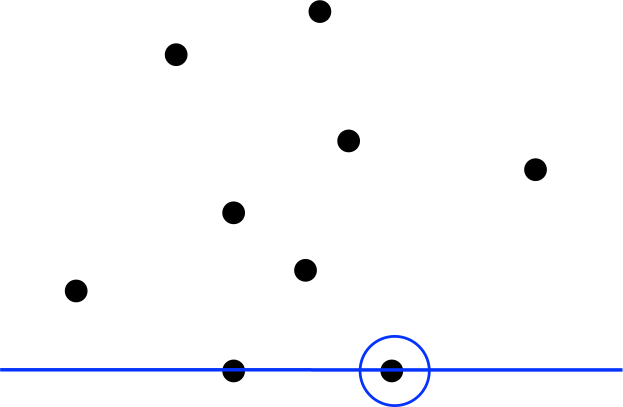
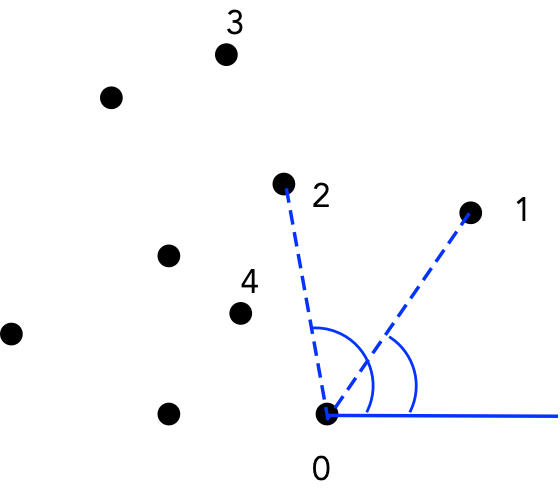
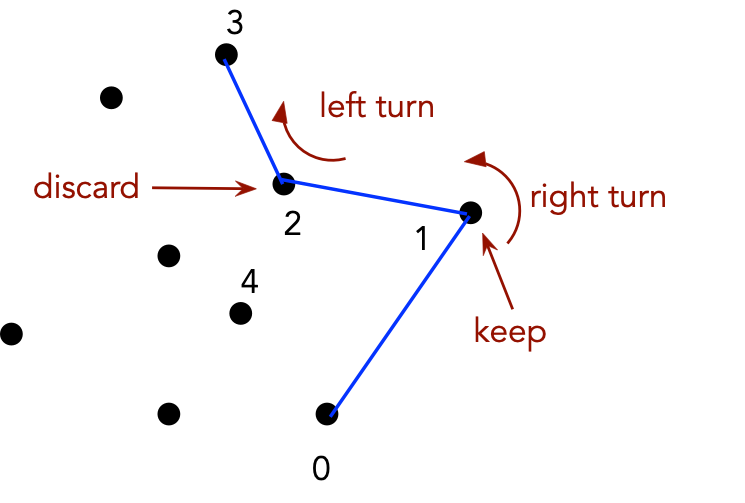
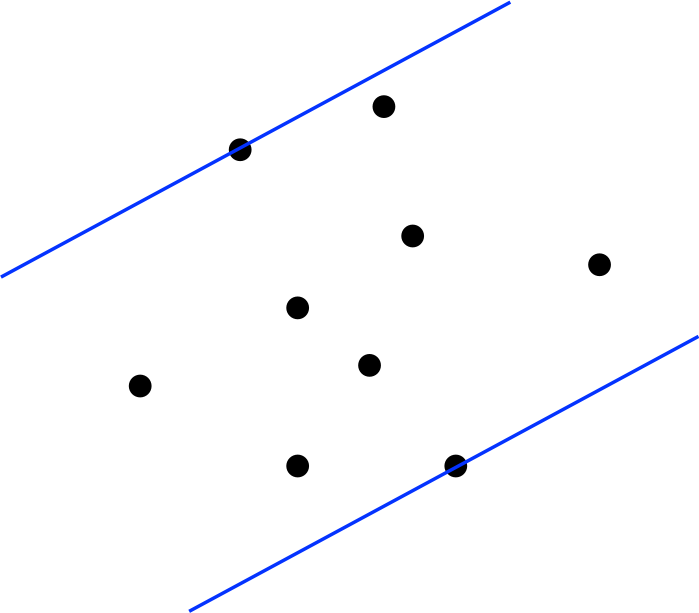
If the center point is at a "right turn", discard that point.
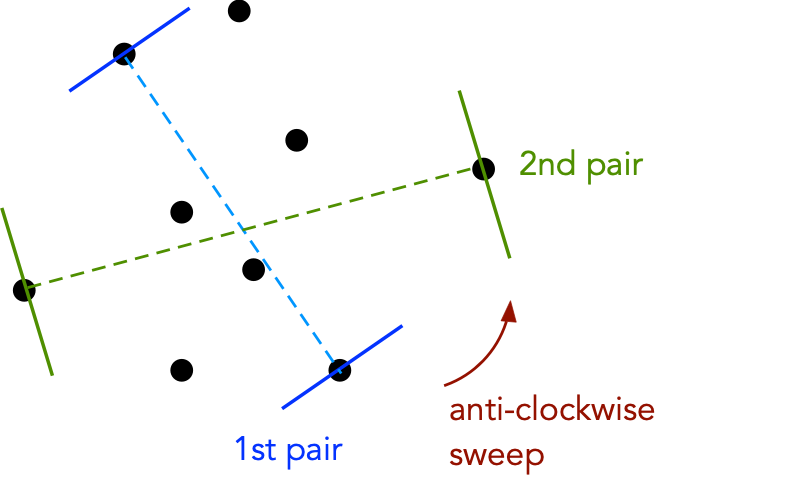
Now, let's take a first look at the code:
public class AntiPodalAlgorithm {
static double distance (Pointd p, Pointd q)
{
// Return the Euclidean distance between the two points.
}
static double findMaxDistance3 (Pointd[] points, int a, int b, int c)
{
// Compute the distance between each of ab, ac and bc,
// and return the largest.
}
boolean turnComplete = false;
int nextCounterClockwise (Pointd[] points, int i)
{
// Find the next point in the list going counterclockwise,
// that is, in increasing order. Go back to zero if needed.
// Return the array index.
}
int prevCounterClockwise (Pointd[] points, int i)
{
// Similar.
}
int findAntiPodalIndex (Pointd[] hullPoints, int currentIndex, int startAntiPodalIndex)
{
// Given a convex polygon, an index into the vertex array (a particular vertex),
// find it's antipodal vertex, the one farthest away. Start the search from
// a specified vertex, the "startAntiPodalIndex"
}
public double findLargestDistance (Pointd[] points)
{
// 1. Compute the convex hull:
Hull hull = new Hull (points);
// 2. Extract the hull points:
Pointd[] hullPoints = hull.getPoints();
// 3. If it's exactly three points, we have a method just for that:
if (hullPoints.length == 3)
return findMaxDistance3 (hullPoints, 0, 1, 2);
// Otherwise, we start an antipodal scan.
boolean over = false;
// 4. Start the scan at vertex 0, using the edge ending at 0:
int currentIndex = 0;
int prevIndex = prevCounterClockwise (hullPoints, currentIndex);
// 5. Find the antipodal vertex for edge (n-1,0):
int antiPodalIndex = findAntiPodalIndex (hullPoints, currentIndex, 1);
// 6. Set the current largest distance:
double maxDist = findMaxDistance3 (hullPoints, currentIndex, prevIndex, antiPodalIndex);
// We'll stop once we've gone around and come back to vertex 0.
double dist = 0;
turnComplete = false;
// 7. While the turn is not complete:
while (! over) {
// 7.1 Find the next edge:
prevIndex = currentIndex;
currentIndex = nextCounterClockwise (hullPoints, currentIndex);
// 7.2 Get its antipodal vertex:
antiPodalIndex = findAntiPodalIndex (hullPoints, currentIndex, antiPodalIndex);
// 7.3 Compute the distance:
dist = findMaxDistance3 (hullPoints, currentIndex, prevIndex, antiPodalIndex);
// 7.4 Record maximum:
if (dist > maxDist)
maxDist = dist;
// 7.5 Check whether turn is complete:
if (turnComplete)
over = true;
} // end-while
// 8. Return largest distance found.
return maxDist;
}
} // End-class
import java.util.*;
public class Hull {
// Maintain hull points internally:
private Pointd[] hull;
// The data set is given to the constructor.
public Hull (Pointd[] points)
{
Pointd[] vertices;
int i, n;
// Record the number of vertices:
n = points.length;
// 1. Make a copy of the vertices because we'll need to sort:
vertices = new Pointd[n];
System.arraycopy (points, 0, vertices, 0, n);
// 2. Find the rightmost, lowest point (it's on the hull).
int low = findLowest (vertices);
// 3. Put that in the first position and sort the rest by
// angle made from the horizontal line through "low".
swap (vertices, 0, low);
HullSortComparator comp = new HullSortComparator (vertices[0]);
Arrays.sort (vertices, 1, vertices.length-1, comp);
// 4. Remove collinear points:
n = removeCollinearPoints (vertices);
// 5. Now compute the hull.
hull = grahamScan (vertices, n);
}
Pointd[] grahamScan (Pointd[] p, int numPoints)
{
// 1. Create a stack and initialize with first two points:
HullStack hstack = new HullStack (numPoints);
hstack.push (p[0]);
hstack.push (p[1]);
// 2. Start scanning points.
int i = 2;
// 3. While scan not complete:
while (i < numPoints)
{
// 3.1 If the current point is on the hull, push next one.
// We know a point is potentially on the hull if the
// the angle is convex (a left turn).
if ( hstack.isHull (p[i]) )
hstack.push (p[i++]);
// Else remove it.
else
hstack.pop ();
// NOTE: the isHull() method looks for "left" and "right" turns.
}
// 4. Return all points still on the stack.
return hstack.hullArray();
}
private int findLowest (Pointd[] v)
{
// 1. Scan through points:
// 1.1 If y-value is lower, the point is lower. If the y-values
// are the same, check that the x value is further to the right:
// 2. Return lowest point found:
}
int removeCollinearPoints (Pointd[] p)
{
// Not shown
}
void swap (Pointd[] data, int i, int j)
{
// Not shown
}
}
Next, consider this idea:
| # of points | # hull points |
| 10 | 6 |
| 100 | 13 |
| 1000 | 18 |
| 10000 | 25 |
public class HullAlgorithm {
static double distance (Pointd p, Pointd q)
{
// Return the distance between points p and q.
}
public double findLargest (Pointd[] points)
{
// For each pair of points: compute the distance, recording
// the largest such distance:
}
public double findLargestDistance (Pointd[] points)
{
// 1. Find the convex hull:
Hull hull = new Hull (points);
// 2. Extract the points:
Pointd[] hullPoints = hull.getPoints();
// 3. Compute an all-pairs largest-distance:
return findLargest (hullPoints);
}
}
Note:
In-Class Exercise 2: What is this pathological test data? Give an example.
Summary:
Consider the following problem:
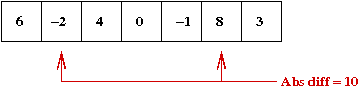
As a first attempt to solve this problem, consider (source file):
static void algorithm1 (double[] A)
{
// 1. Set the initial maximum to the difference between the first two:
double max = Math.abs (A[0] - A[1]);
// 2. Record the actual values:
double x = A[0], y = A[1];
// 3. Now compare each pair of numbers:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
// 3.1 For each such pair, see if it's difference is larger
// than the current maximum.
double diff = Math.abs (A[i] - A[j]);
if (diff > max) {
// 3.1.1 If so, record the new maximum and the values
// that achieved it.
max = diff;
x = A[i];
y = A[j];
}
} // inner-for
} // outer-for
// 4. Output:
System.out.println ("Algorithm 1: the numbers: " + x + "," + y
+ " difference=" + max);
}
Here are some timings for different array sizes (in milliseconds):
| Array size | execution time |
| 1000 | 84 |
| 2000 | 258 |
| 3000 | 554 |
| 4000 | 985 |
| 5000 | 1551 |
| 6000 | 2228 |
| 7000 | 3031 |
| 8000 | 3962 |
| 9000 | 5020 |
| 10000 | 6247 |
How could we improve this program?
| Array size | Java | C |
| 7000 | 3031 | 2670 |
| 8000 | 3962 | 3490 |
| 9000 | 5020 | 4430 |
| 10000 | 6247 | 5490 |
So, it is faster but compare this with Algorithm2 (in Java):
| Array size | Algorithm1 (Java) | Algorithm1 (C) | Algorithm2 (Java) |
| 7000 | 3031 | 2670 | 47 |
| 8000 | 3962 | 3490 | 49 |
| 9000 | 5020 | 4430 | 49 |
| 10000 | 6247 | 5490 | 56 |
In-Class Exercise 3: In what other ways can the original Java program be improved?
Instead, let's consider some algorithmic improvements:
static void algorithm2 (double[] A)
{
// 1. Sort the array:
Arrays.sort (A);
// 2. The smallest is first, the largest last:
double diff = A[A.length-1] - A[0];
// 3. Output:
System.out.println ("Algorithm 2: the numbers: " + A[0] + "," + A[A.length-1]
+ " difference=" + diff);
}
static void algorithm3 (double[] A)
{
// 1. Initialize min and max:
double min = A[0];
double max = A[0];
// 2. Scan through array finding the latest min and max:
for (int i=1; i < A.length; i++){
if (A[i] < min)
min = A[i];
else if (A[i] > max)
max = A[i];
}
// 3. Output:
double diff = max - min;
System.out.println ("Algorithm 3: the numbers: " + min + "," + max
+ " difference=" + diff);
}
In-Class Exercise 4: Why are algorithms 2 and 3 faster? How many comparisons are made by each algorithm with an array of n elements?
In-Class Exercise 5: Take your code for Exercise 1, and count the number of times "distance" is computed. For n points, how many times is distance computed?
What this course is about:
Key principles:
Algorithms in the context of the rest of computer science:
What is an algorithm?
What is pseudocode?
1. Scan through all possible pairs of numbers in the array.
2. For each such pair, compute the absolute difference.
3. Record the largest such difference.
Input: an array of numbers, A
1. Set the initial maximum to the difference between the first two
in the array.
2. Loop through all possible pairs of numbers:
2.1 For each such pair, see if it's difference is larger
than the current maximum.
2.1.1 If so, record the new maximum and the values
that achieved it.
3. Output the maximum found.
Algorithm1 (A)
Input: A, an array of numbers.
// Set the initial maximum to the difference between the first two:
1. max = Absolute-Difference (A[0], A[1])
// Record the actual values:
2. x = A[0], y = A[1]
// Now compare each pair of numbers:
3. for i=0 to length-1
4. for j=i+1 to length
// For each such pair, see if it's difference is larger
// than the current maximum.
5. diff = Absolute-Difference (A[i], A[j])
6. if diff > max
// If so, record the new maximum and the values
// that achieved it.
7. max = diff
8. x = A[i], y = A[j]
9. endif
10. endfor
11. endfor
Output: min, max, diff
Note:
Algorithms are analysed using the so-called "order notation":
Consider the following example:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
double diff = Math.abs (A[i] - A[j]);
if (diff > max)
max = diff;
}
}
Let's analyse this piece of code:
First, it's preferable to use math symbols:
\begin{eqnarray} \sum_{i=0}^{n-2} \sum_{j=i+1}^{n-1} s & \;\;\;= \;\;\; & s \sum_{i=0}^{n-2} (n - i - 1) \\ & \;\;\; = \;\;\; & s \sum_{j=n-1}^{1} j \\ & \;\;\; = \;\;\; & s \sum_{j=1}^{n-1} j \\ & \;\;\; = \;\;\; & s \frac{n(n-1)}{2}\\ \end{eqnarray}
It is possible to simplify further by observing that $$ \frac{n(n-1)}{2} = \frac{n^2}{2} - \frac{n}{2} $$
Observe: the term that dominates is $$ \frac{n^2}{2} $$
Accordingly, for purposes of approximate analysis:
Let's try a thought experiment: first, we'll rewrite the nested for-loop as:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
// Instead of:
//double diff = Math.abs (A[i] - A[j]);
//if (diff > max)
//max = diff;
// We'll represent the "work done at each step" as:
System.out.print (" X");
}
System.out.println ();
}
In-Class Exercise 6: What is the resulting output? Think of each X as a visual way of representing the "work done" inside the earlier version of the loop. Draw the result for n=8. For an array of length \(n\), how many X's are printed?
A quick math review:
In-Class Exercise 7:
Plot the following functions in the range
(0,100) by "joining the dots" of function values computed
at 0, 10, 20, ..., 100:
In-Class Exercise 8: Use the definition of logarithms and the exponentiation rules to show that: \(\log_a(xy) = \log_a(x) + \log_a(y)\).
The key things to remember about order notation:
An important thing to remember:
In-Class Exercise 9:
Download and execute TwoFunction.java.
You will also need Function.java
and SimplePlotPanel.java.
We'll now try and work towards a formal definition:
In-Class Exercise 10: Consider \(f(n) = 9n^2\) and \(g(n) = n^2\). Is \(f(n) = O(g(n)) \)?
In-Class Exercise 11: Consider \(f(n)=9n^2\) and \(g(n) = n^2\) What choice of \(c\) suffices to show \(f(n) = O(g(n)\) by the above definition?
In-Class Exercise 12: Consider \(f(n) = 9n^2 + 1000n\) and \(g(n) = n^2\). Is there a choice of \(c\) such that \(f(n) = O(g(n)\) by the above definition?
In-Class Exercise 13: Consider \(f(n) = 9n^2 + 1000n\) and \(g(n) = n^2\). Suppose \(c=10\). Is there a value of \(N\) such that \(f(n) \leq c g(n)\) for all \(n > N\)? Plot f and g by modifying the code in TwoFunction.java. Change the upper limit of the for-loop to 2000.
In-Class Exercise 14: What value of \(N\) is sufficient when \(c=1000\)?
In-Class Exercise 15: Can you show that definitions 3 and 4 are equivalent?
In-Class Exercise 16: Show how Fact 1 implies Fact 2.
The two ways in which we use Big-Oh:
// ... stuff ...
for i=0 to length-1
for j=i+1 to length
// ... more stuff ...
In-Class Exercise 17:
Implement and analyze the Selection Sort algorithm:
Consider comparing two algorithms A and B on the sorting problem:
Typical worst-case analysis:
Theoretical average-case analysis:
Experimental average-case analysis:
A comprehensive analysis of a problem:
Use the System.currentTimeMillis() method:
long startTime = System.currentTimeMillis();
// ... algorithm runs here ...
double timeTaken = System.currentTimeMillis() - startTime;
In-Class Exercise 18: Compare your selection sort implementation with the sort algorithm in the Java library. Download SelectionSortTiming.java and insert your code from the previous exercise.
A brief mention of some "famous" algorithms and data structures:
In-Class Exercise 19:
Do a web search on "top ten algorithms". What do you see?