By the end of this module, you will be able to:
We will first consider two aspects of keys:


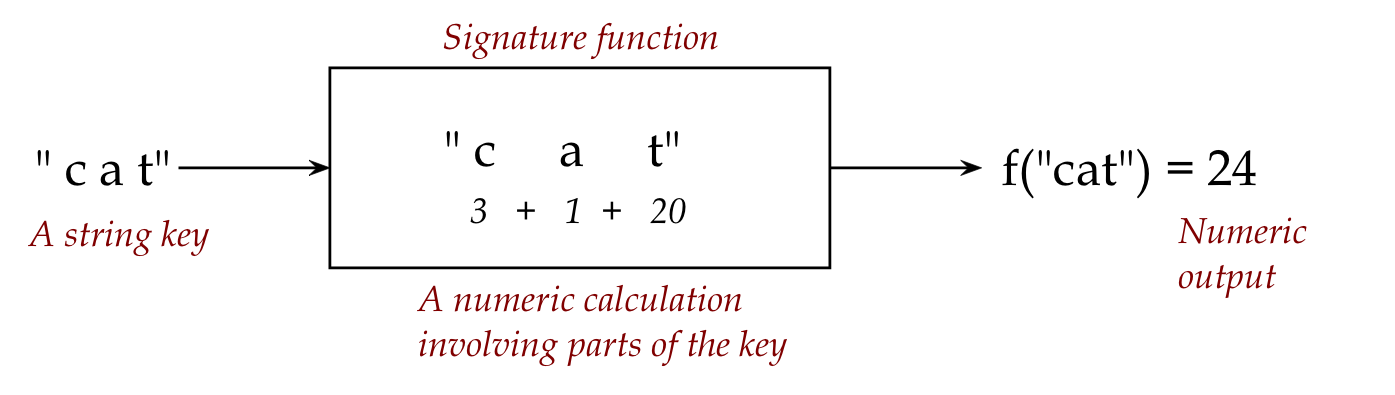
Signatures (of keys):
In-Class Exercise 4.1: Compare the two signatures, "first-letter-of-string" and "concatenation-of-ascii-codes", with regard to uniqueness, brevity, efficiency and order-preservation.
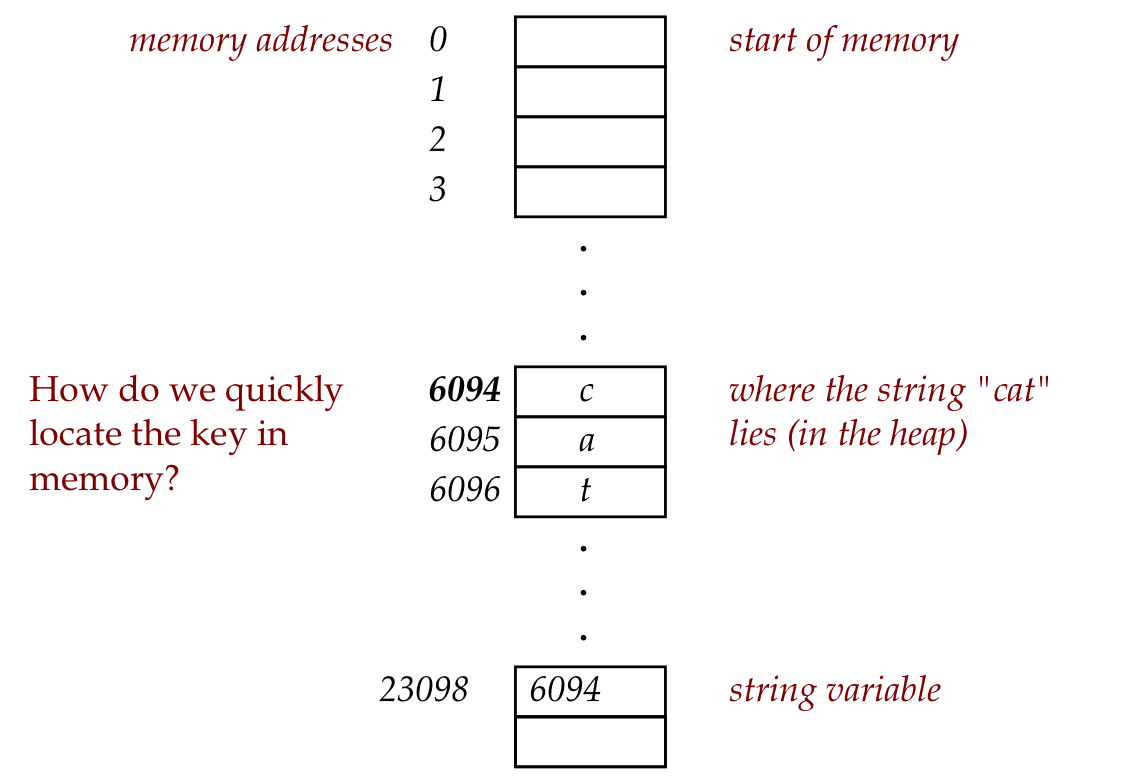
Addresses (of keys):
Key ideas:
Two problems:
Details:

Example:
"catch", "throws", "break", "byte", "volatile", "throw", "protected", "this", "do", "switch", "boolean", "char", "package", "true", "extends", "new", "instanceof", "for", "public", "return", "while", "case", "abstract", "false", "void", "synchronized", "implements", "finally", "null", "try", "const", "default", "native", "continue", "super", "import", "class", "final", "transient", "short", "double", "long", "private", "goto", "int", "if", "else", "static", "interface", "float"



Pseudocode:
Algorithm: initialize (numBuckets) Input: desired number of buckets 1. Initialize array of linked lists;
Algorithm: insert (key, value)
Input: key-value pair
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
// No list present, so create one
3. table[entry] = new linked list;
4. table[entry].add (key, value)
5. else
6. // Otherwise, add to existing list
7. table[entry].add (key, value)
8. endif
Algorithm: search (key)
Input: search-key
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
3. return null
4. else
5. return table[entry].search (key)
6. endif
Output: value, if found; null otherwise.
About signatures:
a: 1 ("abstract")
b: 3 ("boolean", "break", "byte")
c: 6 ("case", "catch", "char", "class", "const", "continue")
d: 3 ("default", "do", "double")
e: 2 ("else", "extends")
f: 5 ("false", "final", "finally", "float", "for")
g: 1 ("goto")
h: 0
i: 6 ("if", "implements", "import", "instanceof", "int", "interface")
j: 0
k: 0
l: 1 ("long")
m: 0
n: 3 ("native", "new", "null")
o: 0
p: 4 ("package", "private", "protected", "public")
q: 0
r: 1 ("return")
s: 5 ("short", "static", "super", "switch", "synchronized")
t: 6 ("this", "throw", "throws", "transient", "true", "try")
u: 0
v: 2 ("void", "volatile")
w: 1 ("while")
x: 0
y: 0
z: 0
table entry 0: 3
table entry 1: 0
table entry 2: 3
table entry 3: 3
table entry 4: 0
table entry 5: 1
table entry 6: 1
table entry 7: 1
table entry 8: 4
table entry 9: 0
table entry 10: 0
table entry 11: 2
table entry 12: 0
table entry 13: 2
table entry 14: 1
table entry 15: 1
table entry 16: 0
table entry 17: 0
table entry 18: 2
table entry 19: 2
table entry 20: 2
table entry 21: 4
table entry 22: 1
table entry 23: 0
table entry 24: 0
table entry 25: 0
(A more even, but not perfect distribution).
int hashValue = 0;
for (int i=0; i < length; i++) {
// Note: 31 = 2**5-1. The string characters are assumed to be
// stored in charArray[].
hashValue = 31*hashValue + charArray[i];
}
return hashValue;
In-Class Exercise 4.2:
Download HashAnalysis.java
and the file words.txt (a dictionary).
Print out the distribution of words (only the number) over
buckets for each of the following signatures:
Hint: you do not have to implement a hashtable to compute these numbers;
you only need to compute the signature, and record statistics.
Sizing a table:
Analysis (assuming few keys per bucket):
Variations:
In-Class Exercise 4.3: Suppose you had to use a hash table for a collection of floating-point numbers: x1, x2,...,xn. Design a hashing function to hash to the signatures 0,...,m (which are integers).
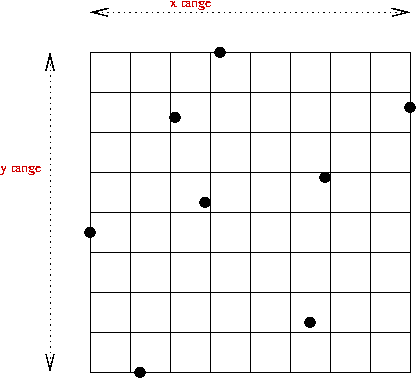
For a collection of points, (x1,y1), (x2,y2), ..., (xn,yn), consider the following queries:
One approach:
2D hashing:
| p1: | (-1.5, 6.25) |
| p2: | (-0.75, 6.1) |
| p3: | (-0.1, 6.33) |
| p4: | (-0.1, 7.1) |
| p5: | (2.1, 6.48) |
| p6: | (2.25, 6.8) |
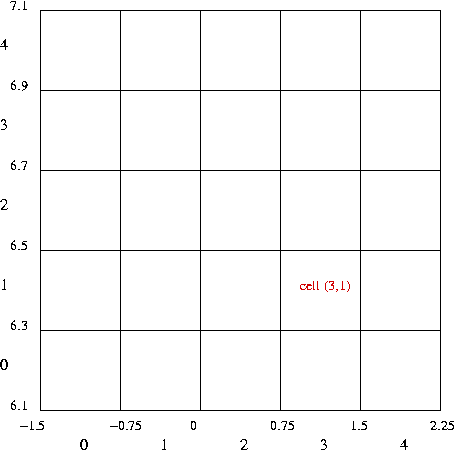
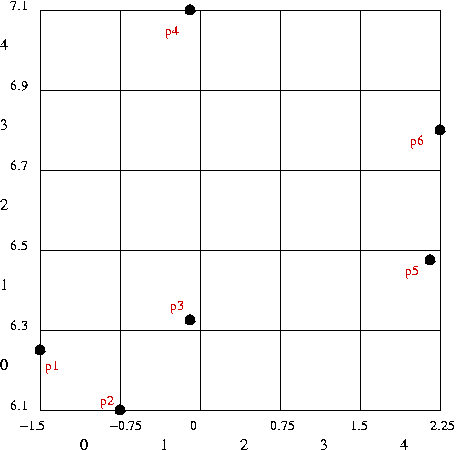
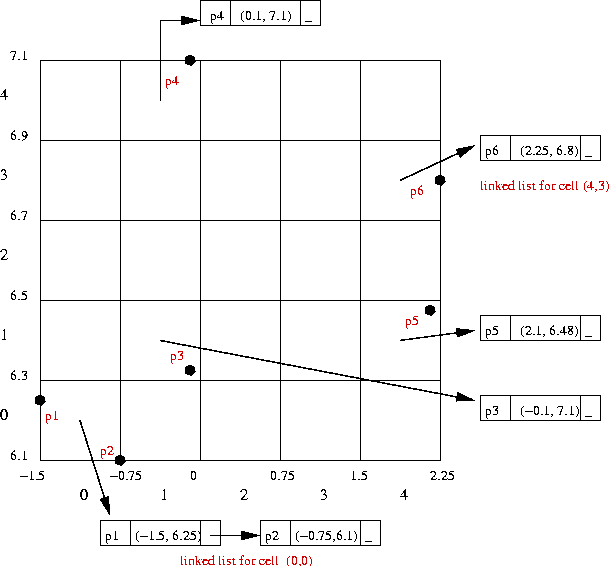
| Point | Coordinates | 2D hash-value |
| p1 | (-1.5, 6.25) | (0,0) |
| p2 | (-0.75, 6.1) | (0,0) |
| p3 | (-0.1, 6.33) | (1,1) |
| p4 | (-0.1, 7.1) | (1,4) |
| p5 | (2.1, 6.48) | (4,1) |
| p6 | (2.25, 6.8) | (4,3) |
In-Class Exercise 4.4: Describe how to efficiently compute the hash value for a point p=(x,y), given m and the bounding rectangle.
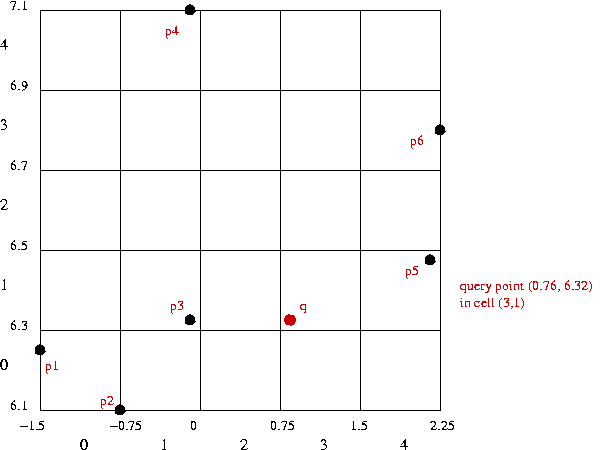
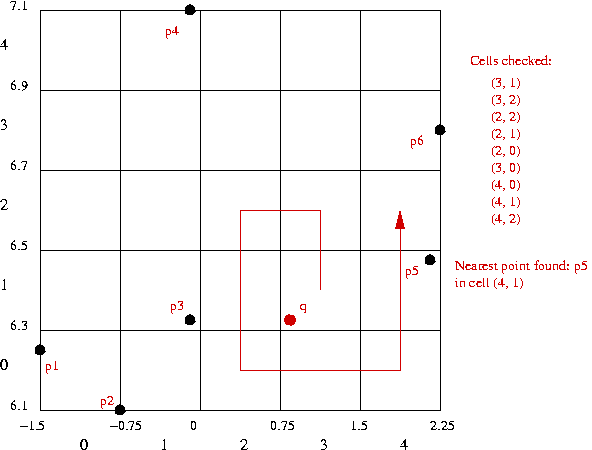
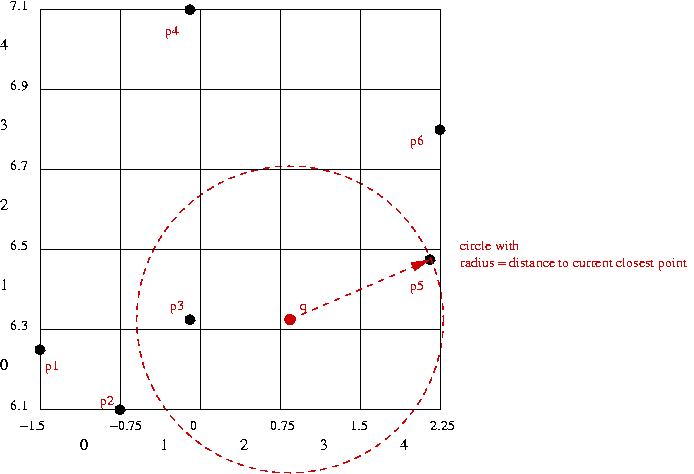
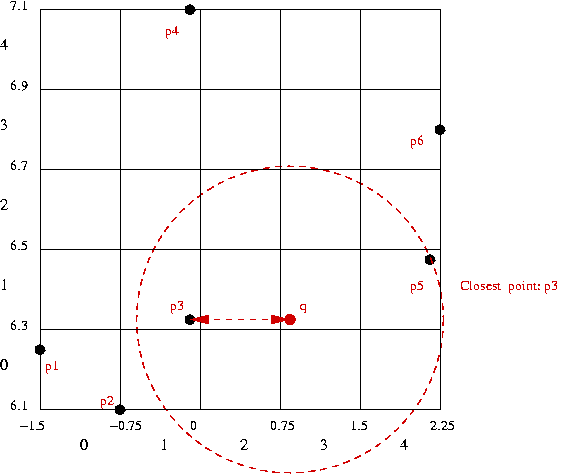
⇒ closest point overall: p3 = (-0.1, 6.33).
In-Class Exercise 4.5: The 2D hashtable above is a 2D-geometric analog of the regular 1D hashtable (that we saw earlier for strings). Design a tree-like data structure for 2D point data that is analogous to the binary trees we used for strings.
Consider combinations of "structure" and whether or not signatures are used:
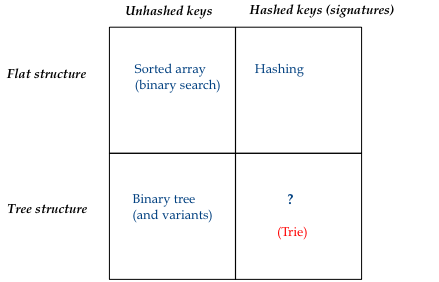
Key ideas:

Key ideas:
Insertion:
| Key | Signature | |
| A | 1000001 | |
| B | 0100001 | |
| C | 1100001 | |
| D | 0010001 | |
| E | 1010001 | |
| F | 0110001 |






Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = create new root with key-value pair;
3. return
4. endif
// Start numbering the bits from 0.
5. recursiveInsert (root, key, value, 0)
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, which bit we are using now
// Compare with node key to see if it's a duplicate.
1. if node.key = key
2. Handle duplicates;
3. return
4. endif
// Otherwise, examine the bitNum-th bit
5. if key.getBit (bitNum) = 0
// Go left if possible, or insert.
6. if node.left is null
7. node.left = new trie node with key-value;
8. else
// Note: at next level we'll need to examine the next bit.
9. recursiveInsert (node.left, key, value, bitNum+1)
10. endif
11. else
// Same thing on the right
12. if node.right is null
13. node.right = new trie node with key-value;
14. else
15. recursiveInsert (node.right, key, value, bitNum+1)
16. endif
17. endif
Search:
Algorithm: search (key) Input: search-key 1. node = recursiveSearch (root, key, 0) 2. if node is null 3. return null 4. else 5. return node.value 6. endif Output: value, if key is found
Algorithm: recursiveSearch (node, key, bitNum)
Input: trie node, search-key, which bit to examine
// Compare with key in node.
1. if node.key = key
// Found.
2. return node
3. endif
// Otherwise, navigate further.
4. if key.getBit (bitNum) = 0
5. if node.left is null
// Not found => search ends.
6. return null
7. else
// Search left.
8. return recursiveSearch (node.left, key, bitNum+1)
9. endif
10. else
11. if node.right is null
// Not found => search ends.
12. return null
13. else
// Search right.
14. return recursiveSearch (node.right, key, bitNum+1)
15. endif
16. endif
Output: trie node if found, else null.
In-Class Exercise 4.6: Use the "ascii code of letter" signature to insert "A B C D E F" into a simple trie. Show all your steps. Ascii codes are available here. Notice what happens and explain why we used "reverse ascii" earlier.
Analysis:
In-Class Exercise 4.7: Why is this true? That is, why is it that n keys need at most log2(n) bits to represent the keys?
Key ideas:

Insertion:
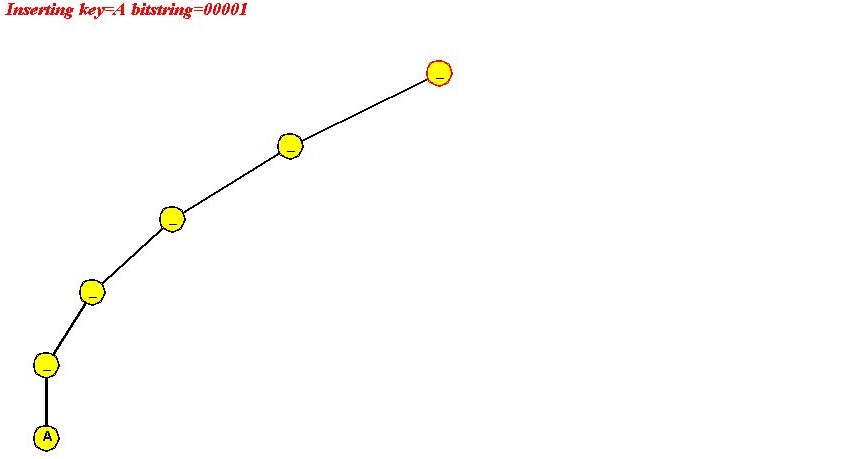
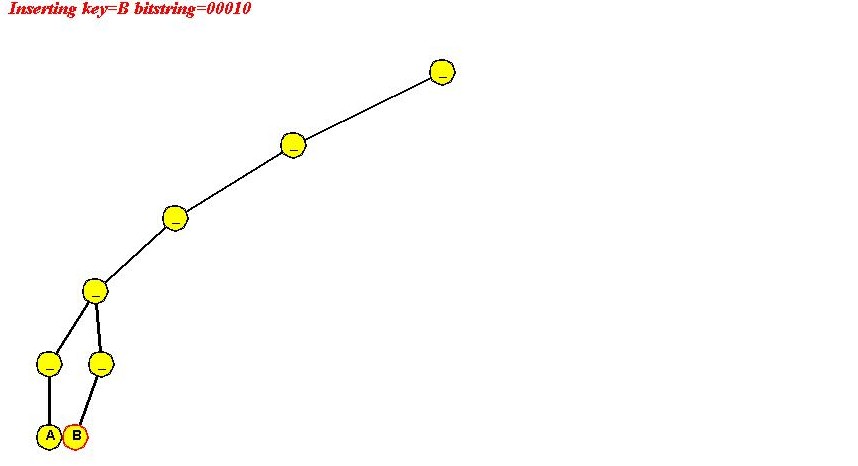
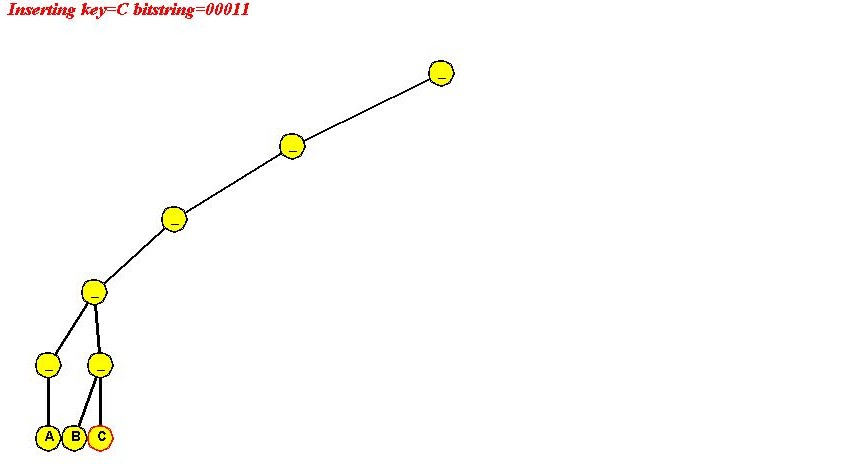
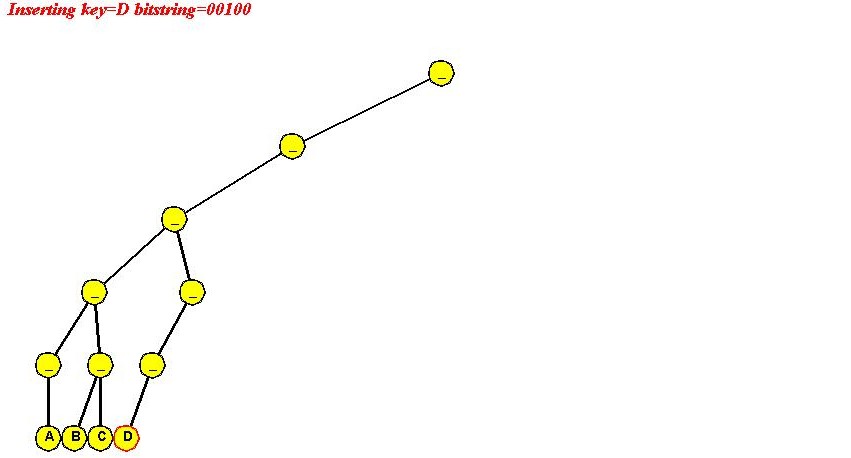
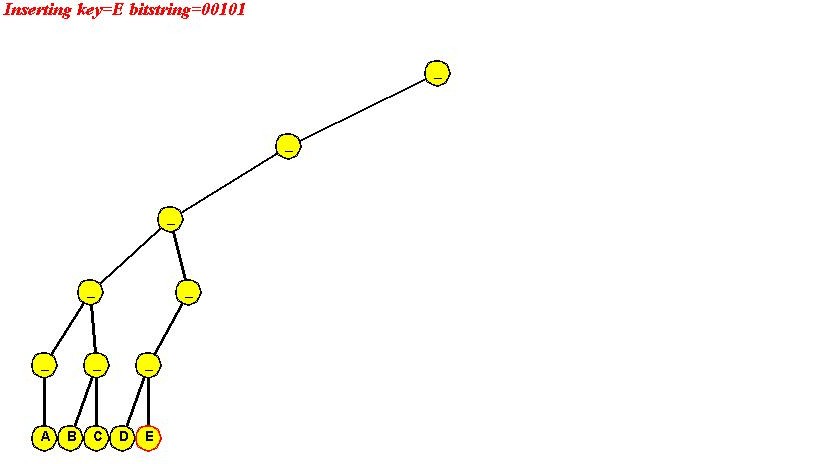
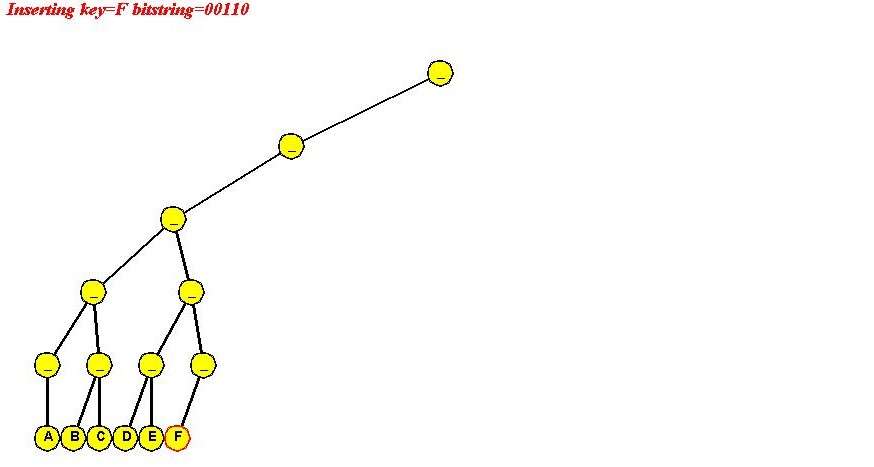
Algorithm: initialize (maxBits)
Input: maximum number of bits
1. Store maximum number of bits to use;
Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = create empty internal node;
// Start bit-numbering at 0 and create path to leaf:
3. extendBranch (root, key, value, 0)
4. return
5. endif
6. recursiveInsert (root, key, value, 0)
Algorithm: extendBranch (node, key, value, bitNum)
Input: internal trie node, key-value pair, bit number
1. Create path of internal nodes from level bitNum to maxBits-1;
2. if key.getBit (maxBits) = 0
3. create left leaf at end of path;
4. else
5. create right leaf at end of path;
6. endif
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, bit number
1. if key.getBit (bitNum) = 0
// Check left side.
2. if node.left is null
// Grow a branch of internal nodes and append leaf.
3. extendBranch (node, key, value, bitNum)
4. else
5. recursiveInsert (node.left, key, value, bitNum+1)
6. endif
7. else
// Check right side.
8. if node.right is null
// Grow a branch of internal nodes and append leaf.
9. extendBranch (node, key, value, bitNum)
10. else
11. recursiveInsert (node.right, key, value, bitNum+1)
12. endif
13. endif
Search:
Sort-order scan:
Analysis:
In-Class Exercise 4.8: Why is it that the full trie wastes O(n) storage? In other words, explain why the number of internal nodes is O(n).
Key ideas:
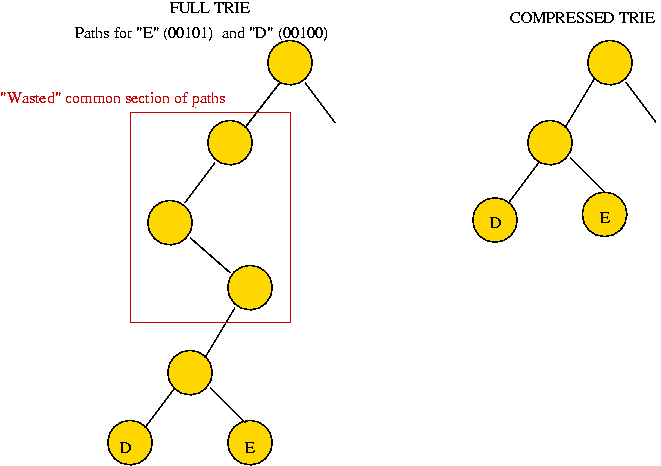
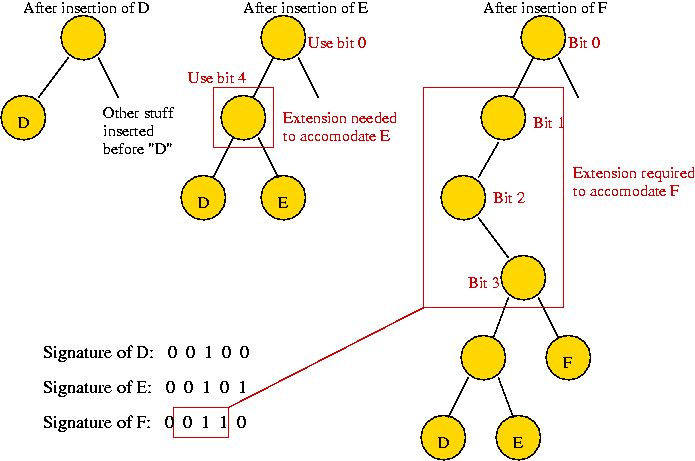
Insertion:

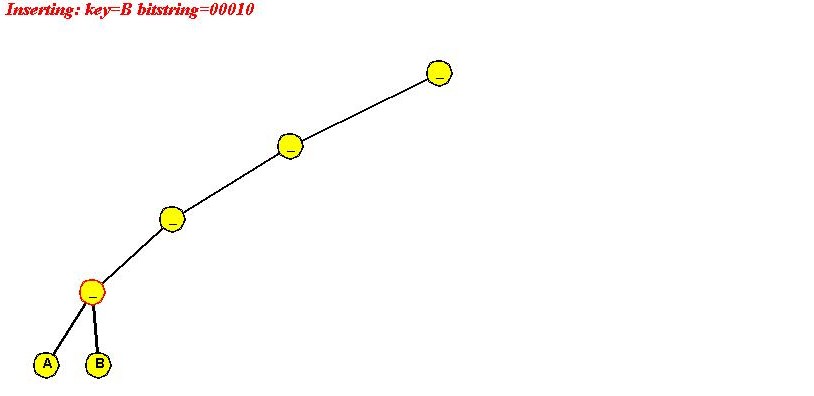
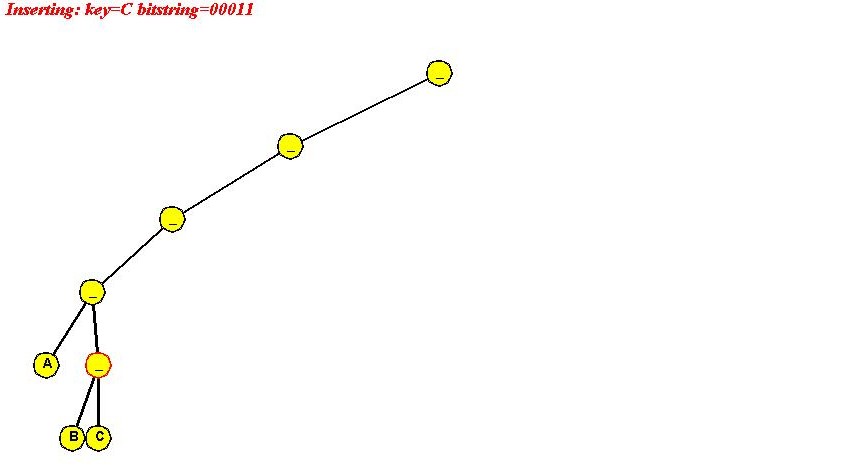
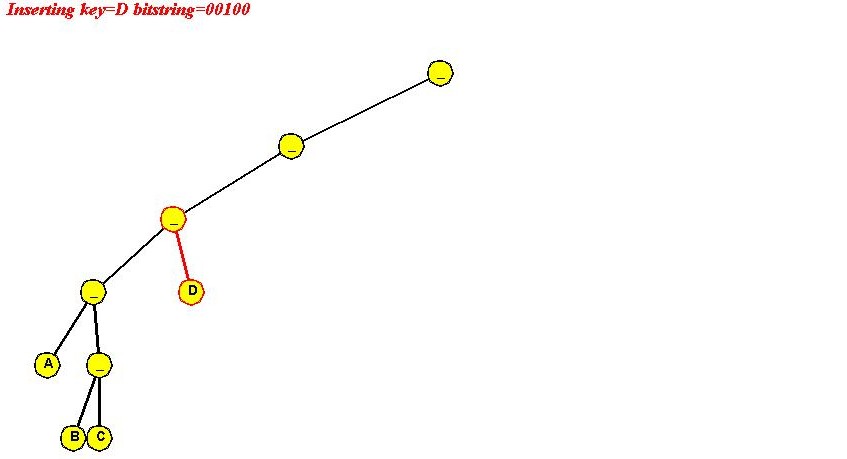
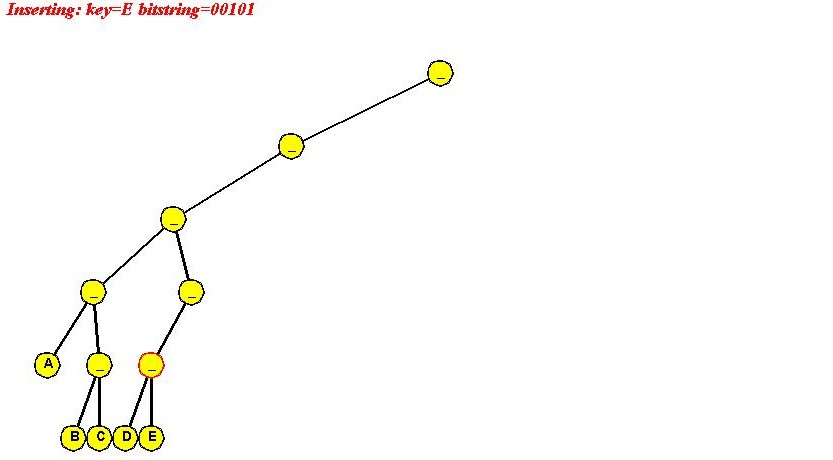
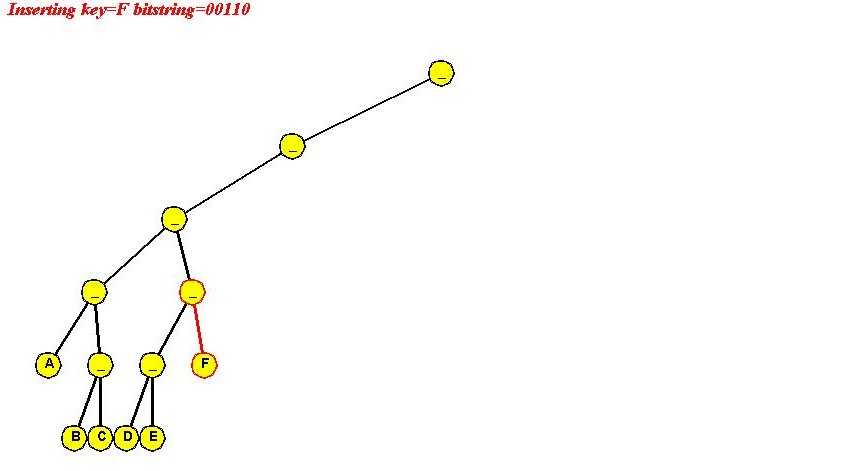
Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = new root node with key-value;
3. return
4. endif
// Start with level 0 (bit number 0):
5. recursiveInsert (root, key, value, 0)
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, bit number
1. if node contains a key
// Need to create a path to distinguish key and node.key
2. extendSmallestBranch (node, node.key, node.value, key, value, bitNum)
3. return
4. endif
// Otherwise, node is an empty interior node for navigation only.
5. if key.getBit (bitNum) = 0
// Check left.
6. if node.left is null
7. node.left = new node containing key-value;
8. else
9. recursiveInsert (node.left, key, value, bitNum+1)
10. endif
11. else
// Check right.
12. if node.right is null
13. node.right = new node containing key-value;
14. else
15. recursiveInsert (node.right, key, value, bitNum+1)
16. endif
17. endif
Algorithm: extendSmallestBranch (node, key1, value1, key2, value2, bitNum)
Input: node from which to build branch, two key-value pairs, bit number.
// Examine bits from bitNum to maxBits.
// As long as the bits are equal in the two keys, extend branch.
// When the bits differ, stop and create children with key1 and key2.
In-Class Exercise 4.9: Use the "reverse ascii code of first letter" signature to insert "A B C D E F" into a compressed trie. Show all your steps. Ascii codes are available here.
Motivation:
Solutions (using Binary Search Tree as data structure):
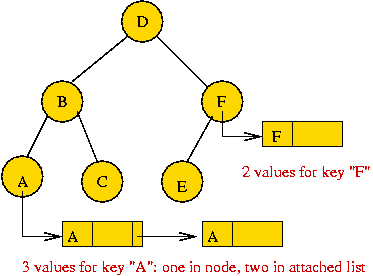
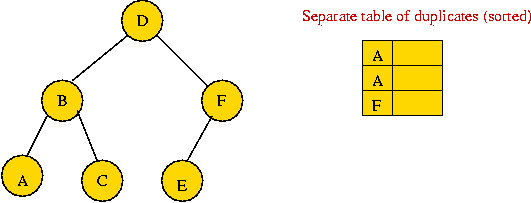
A Java programming trick for handling duplicates: (source file)
import java.util.*;
public class Duplicate {
// Any Map can be used, e.g., TreeMap.
static Map originalDataStructure = new HashMap();
// Insertion.
static void insert (Object key, Object value)
{
// 1. Attempt a direct insertion.
Object oldValue = originalDataStructure.put (key, value);
// 2. If the value wasn't already there, nothing to be done.
if (oldValue == null) {
// No duplicates.
return;
}
// 3. Otherwise, check if duplicates already exist.
if (oldValue instanceof HashSet) {
// 3.1 There are, so add the new one.
HashSet duplicates = (HashSet) oldValue;
duplicates.add (value);
}
else {
// 3.2 This is the first duplicate => create a HashSet to store duplicates.
HashSet duplicates = new HashSet ();
// 3.3 Place old value and duplicate in hashset.
duplicates.add (oldValue);
duplicates.add (value);
// 3.4 Add the hashset itself as the value.
originalDataStructure.put (key, duplicates);
}
}
// Enumerate and print all values.
static void printAll ()
{
Collection values = originalDataStructure.values();
for (Iterator i=values.iterator(); i.hasNext(); ) {
Object obj = i.next();
// If the value is a HashSet, we have duplicates.
if (obj instanceof HashSet) {
// Extract the different values.
HashSet duplicates = (HashSet) obj;
for (Iterator j=duplicates.iterator(); j.hasNext(); ) {
System.out.println (j.next());
}
}
else {
// If it's not a HashSet, the extract obj is a value.
System.out.println (obj);
}
}
}
public static void main (String[] argv)
{
// Add data with duplicates.
insert ("Ali", "Addled Ali");
insert ("Bill", "Bewildered Bill");
insert ("Bill", "Befuddled Bill"); // Duplicate.
insert ("Chen", "Cantankerous Chen");
insert ("Dave", "Discombobulated Dave");
insert ("Dave", "Distracted Dave"); // Duplicate.
insert ("Dave", "Disconcerted Dave"); // Duplicate.
insert ("Ella", "Egregious Ella");
insert ("Franco", "Flummoxed Franco");
insert ("Gita", "Grumpy Gita");
insert ("Gita", "Grouchy Gita"); // Duplicate.
// Print.
printAll();
}
}