Note 11: Trees

We have seen, with linked lists, data structures defined not by a strict sequence ordering, but by a collection of nodes, where nodes point to successive nodes.

• In a linked list, each node specifies one “next” node
• In a tree, each node can have multiple descendant nodes

One example of a tree structure is a binary tree. A basic binary tree consists of nodes, with each node having at most two children:

Trees are not, in the general case, limited to a binary structure, and can have an arbitrary number of children:

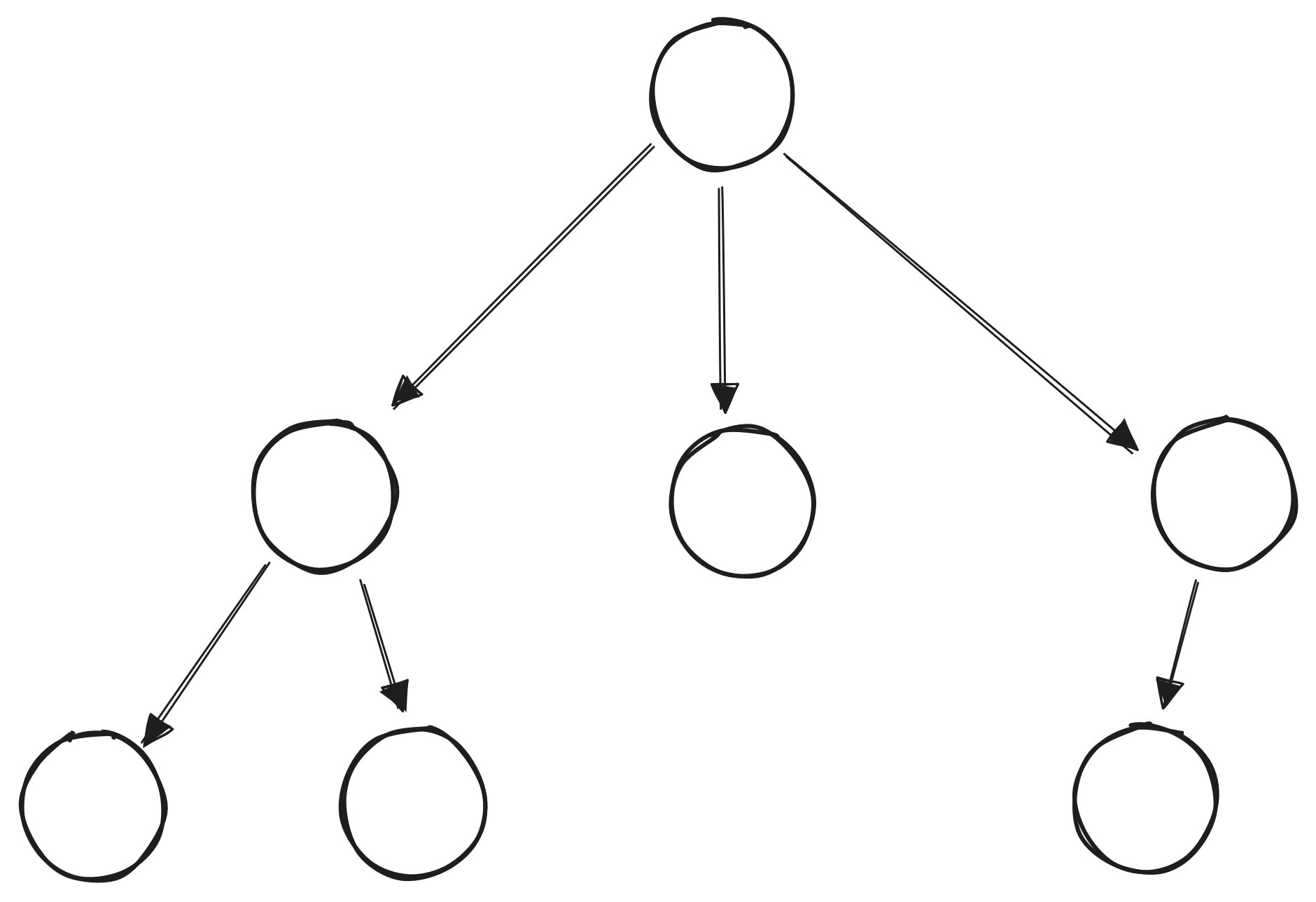
Implementing a basic binary tree is similar to a linked list. We’ll start with a Node:

class Node:
    def __init__(self, key) -> None:
        self.key = key
        self.left = None
        self.right = None

    def update_left(self, new_left) -> None:
        self.left = new_left

    def update_right(self, new_right) -> None:
        self.right = new_right

Unlike linked lists, which have a fixed number of ends, there is no single natural place to add a new element to trees in general:

• We could add elements wherever we want
• We could add elements according to some algorithm

Adding elements according to some algorithm often produces a tree with a structure which we are later able to exploit.

Binary Search Trees

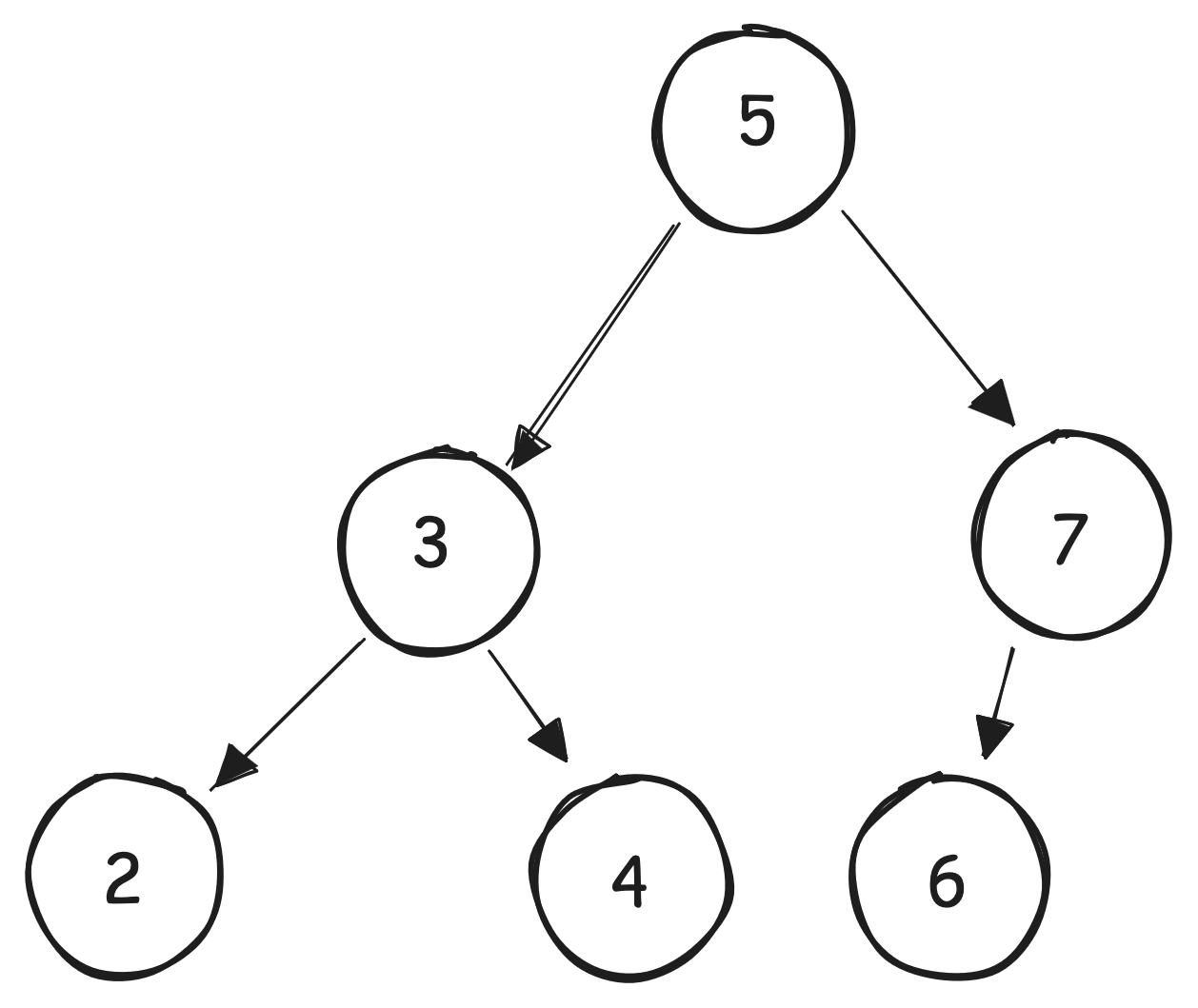
A binary search tree is any binary tree that follows the following scheme:

• Each node has a key
  • Keys can be ordered
• All nodes in the left subtree of any node have keys less than (or equal to) that node’s key
• All nodes in the right subtree of any node have keys greater than that node’s key

Illustrated:

To implement a binary search tree, we need to implement the correct algorithm for adding a new node:

First, we make a node suited for this tree:

class BSTNode:
    def __init__(self, key) -> None:
        self.key = key
        self.left = None
        self.right = None

    def add_child(self, child) -> None:
        if child.key <= self.key:
            if self.left is None:
                self.left = child
            else:
                self.left.add_child(child)
        else:
            if self.right is None:
                self.right = child
            else:
                self.right.add_child(child)

Implementing the tree itself is simple:

class BinarySearchTree:
    def __init__(self) -> None:
        self.root = None
   
    def add_node(self, node) -> None:
        if self.root == None:
            self.root = node
        else:
            self.root.add_child(node)      

Note how add_child is recursive:

• The correct position (left/right) is determined
  • The base case is when there is no node in the correct position
    • The new node is added as a child
  • The recursive case is called on the correct position
    • The algorithm checks that node, its children, and so forth…
    • …until the base case is reached

Modify this binary search tree in the practice problems.

Binary Heaps

A binary heap is a special kind of binary tree with the following characteristics:

• It is complete: each layer is completely full, except possibly the last layer
• It is ordered:
  • For a max heap, each parent node is \(\geq\) its children
  • For a min heap, each parent node is \(\leq\) its children
  • The ordering rule does not place any conditions on nodes other than parents and children, e.g. siblings, “cousins,”” etc.

The below is an example of a valid max heap:

The below is an example of an invalid max heap, due to the three not being completely full on all layers other than the last:

Binary Heap Operations

Heaps are useful because they can perform both an “add to heap” and “extract maximum element” (or minimum element) operations in \(O(log n)\) time. This makes them the most efficient implementation for priority queues: recall the efficiency of our previous implementations of the priority queue.

Here are the binary heap operations, illustrated for a min heap:

Add To Heap

• The new element is added in the leftmost “free” position in the tree.
• If the element is smaller than its parent, swap with parent.
• If the element is not smaller than its parent, or if it now the root, stop.
• Repeat comparisons and swaps with parent

Remove Minimum

• Move the “last” (rightmost element in the bottom layer) of the heat to the root, removing the original root
• If the new root element is larger than its smallest child: swap
• Continue checking this element against the smallest child

Heap Operations, Illustrated

To illustrate, we’ll start with the following heap:

A new element is added in the leftmost free position:

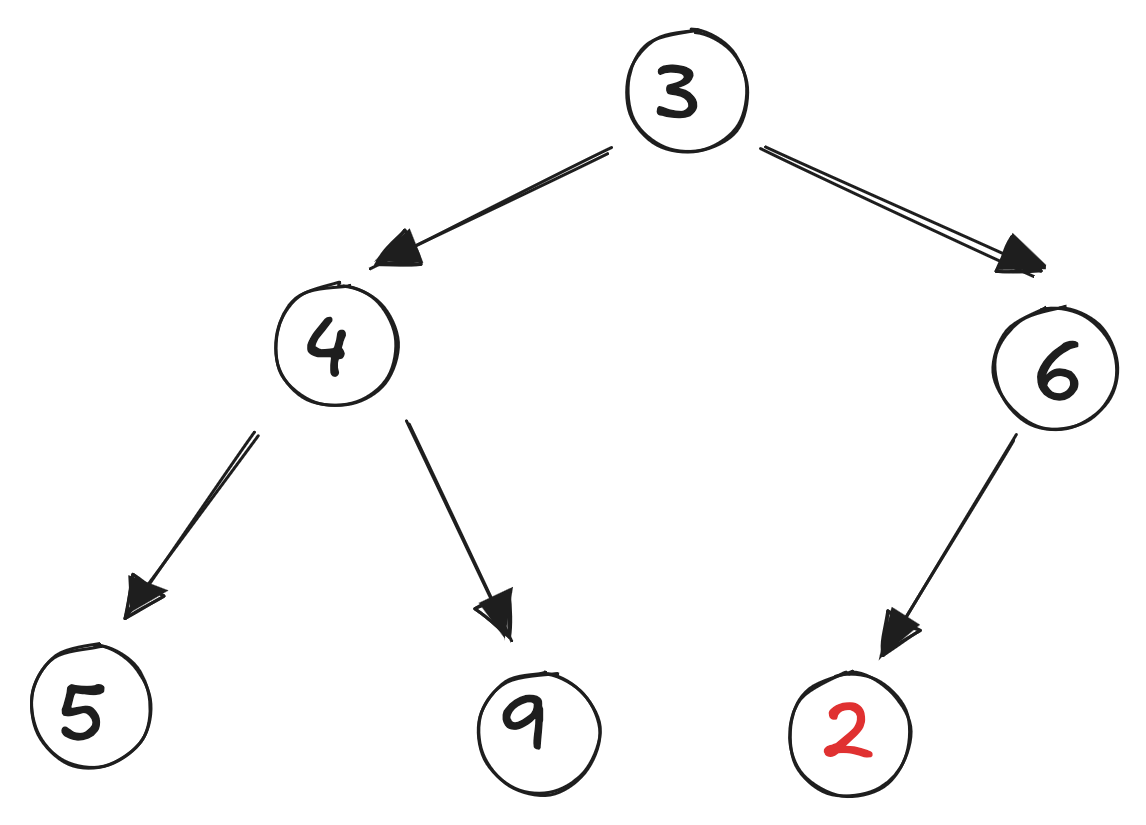
It’s less than its parent, so it is swapped with the parent:

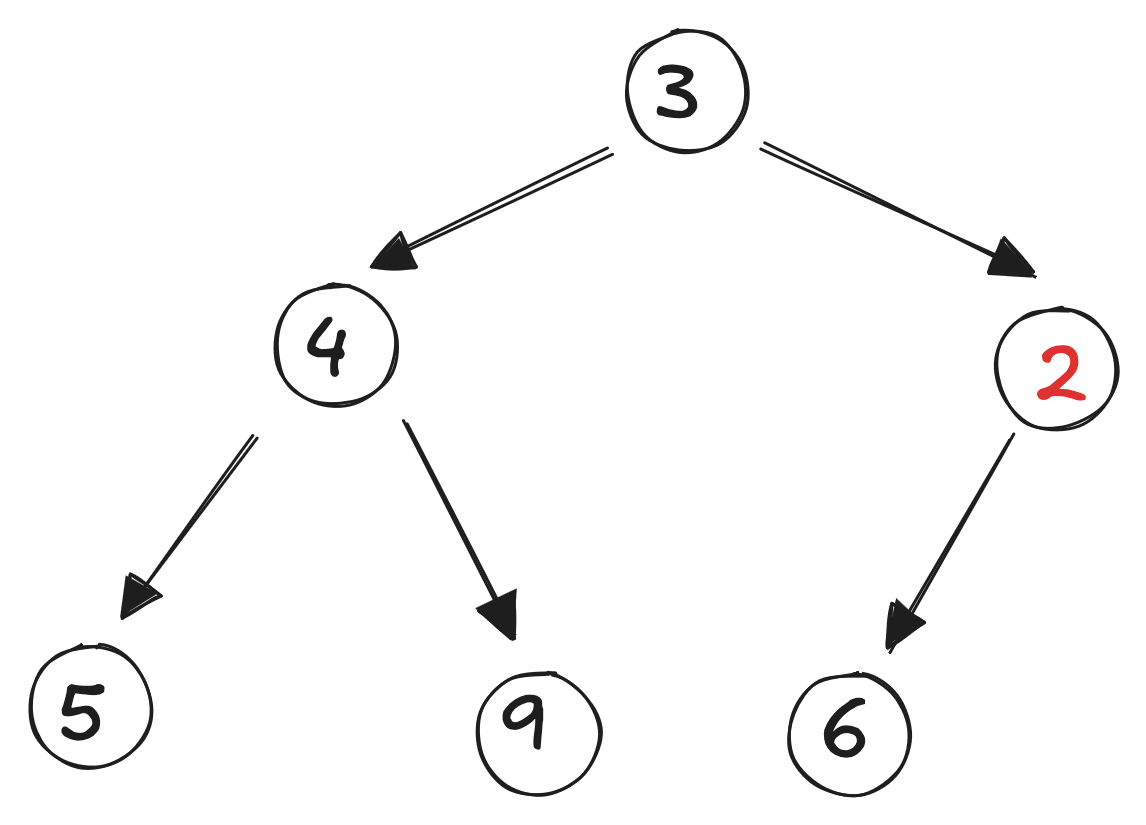
It’s again less than its parent, so it is swapped with the parent:

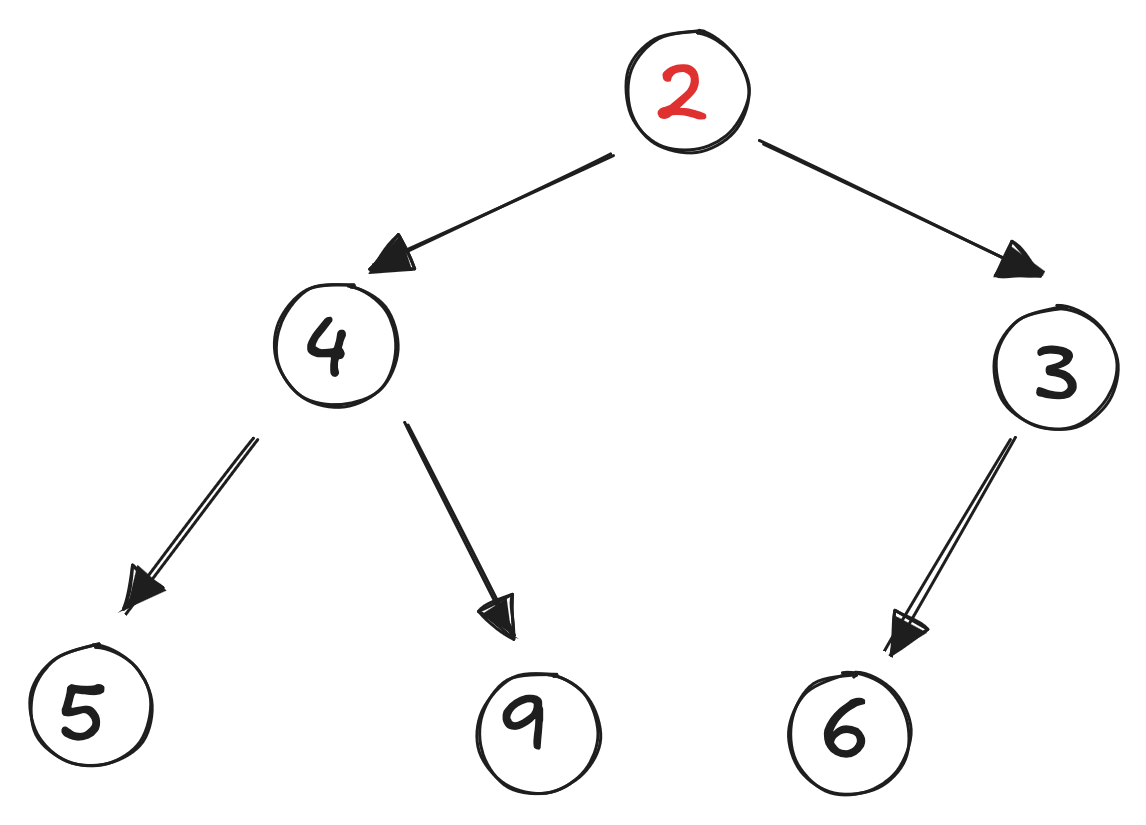
Since the new element is now the root, it has no parent, and adding the element is complete.

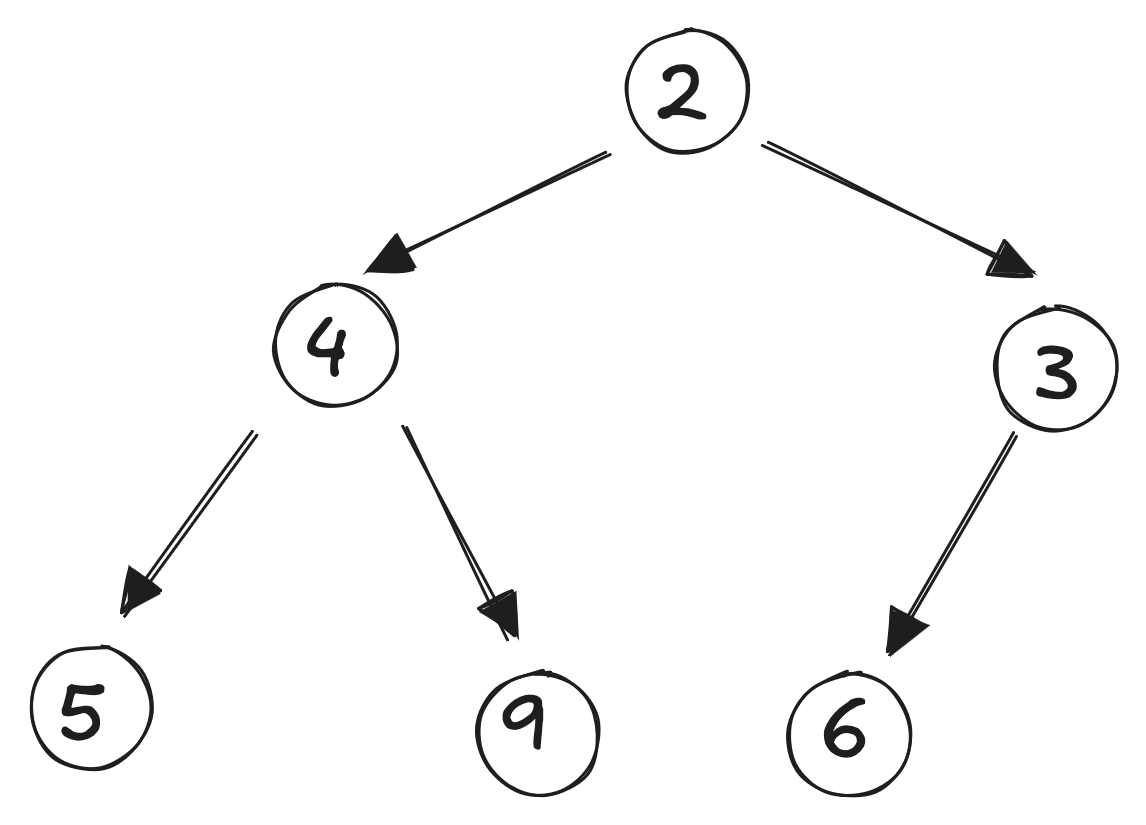
We now extract the minimum element:

Move the “last” element in the tree to the root position:

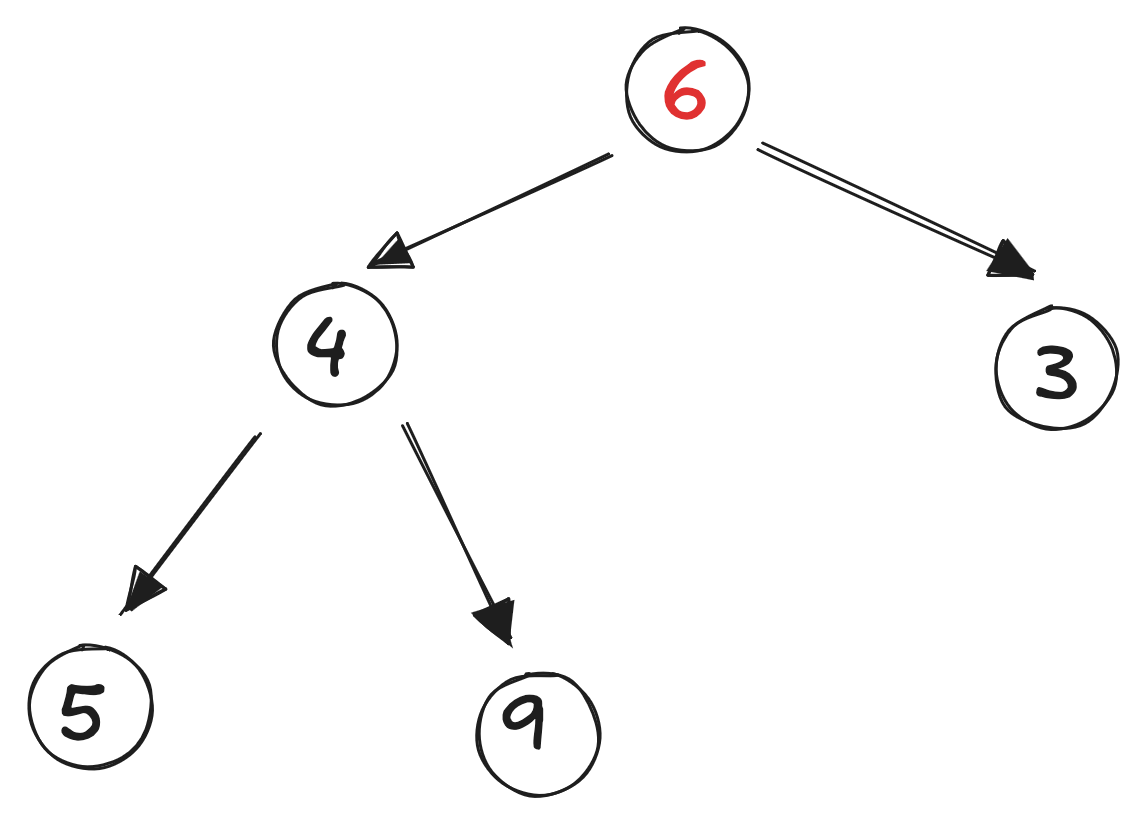
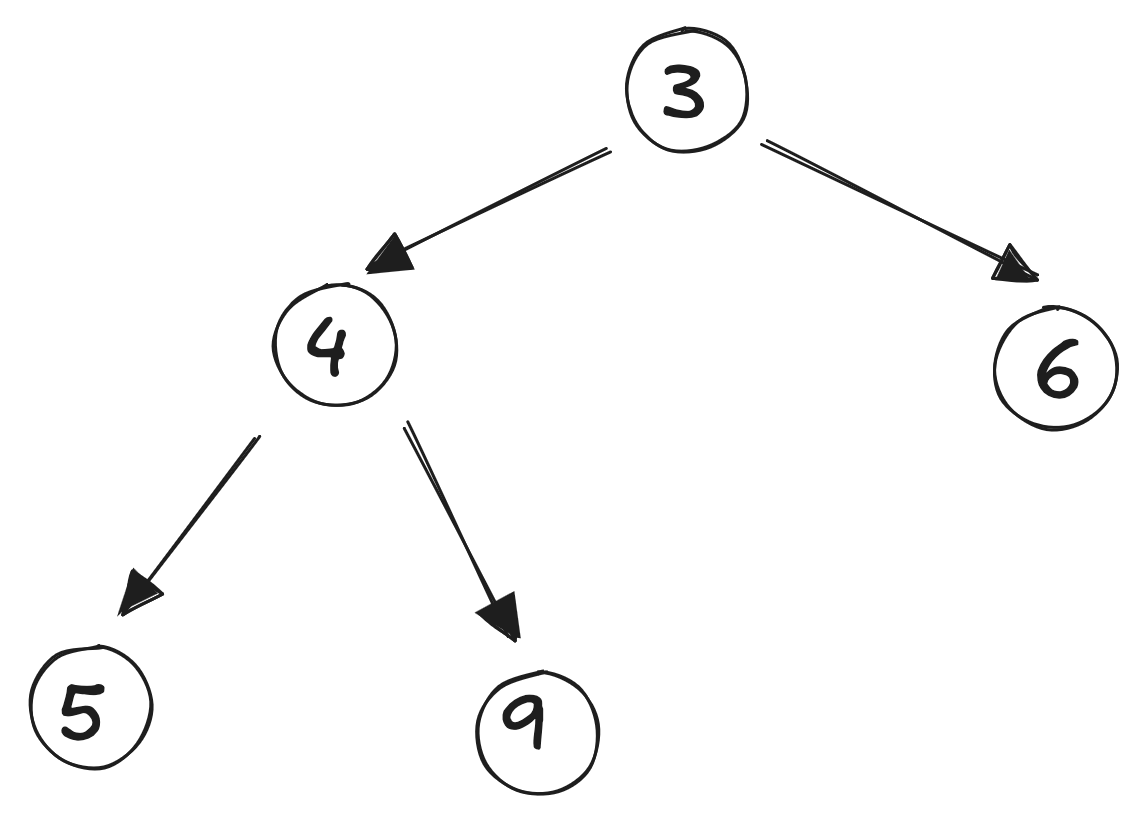
Compare it to its smallest child: since it’s less than the child, swap:

Extraction of the smallest element is now complete.

If we add an element into the last position and it isn’t smaller than its parent, there’s nothing to do:

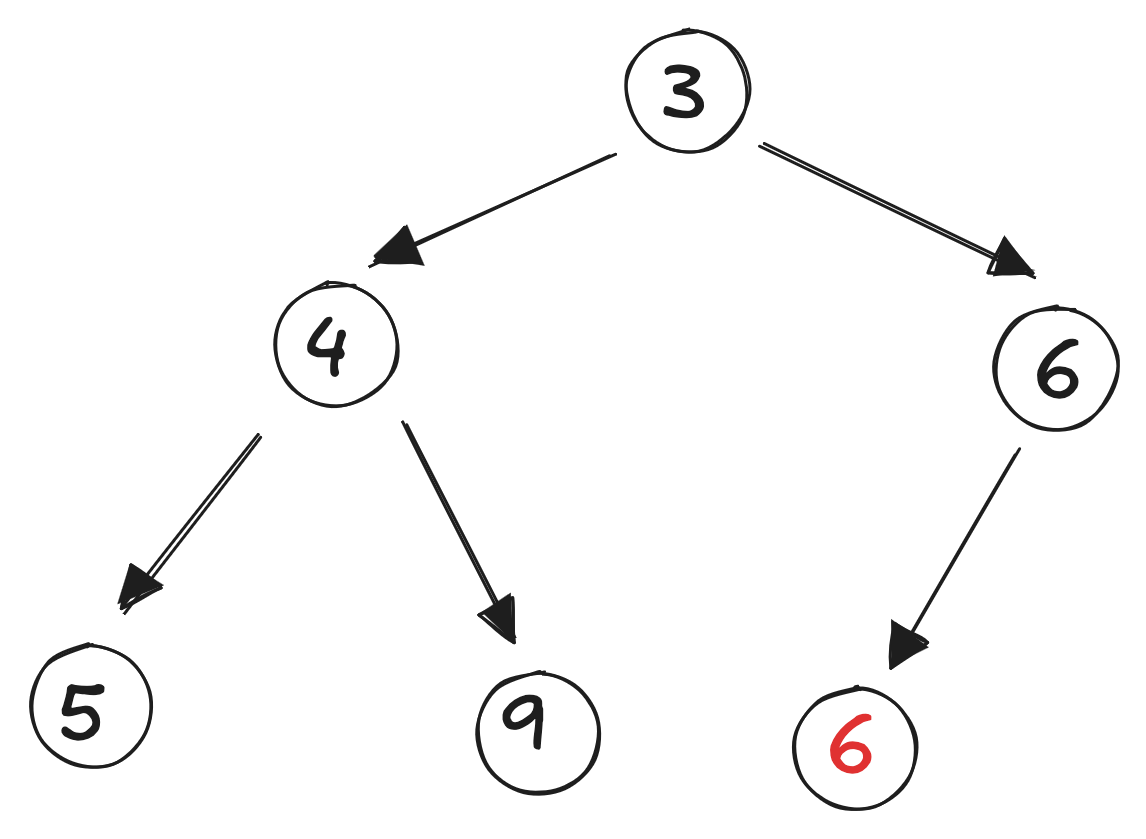
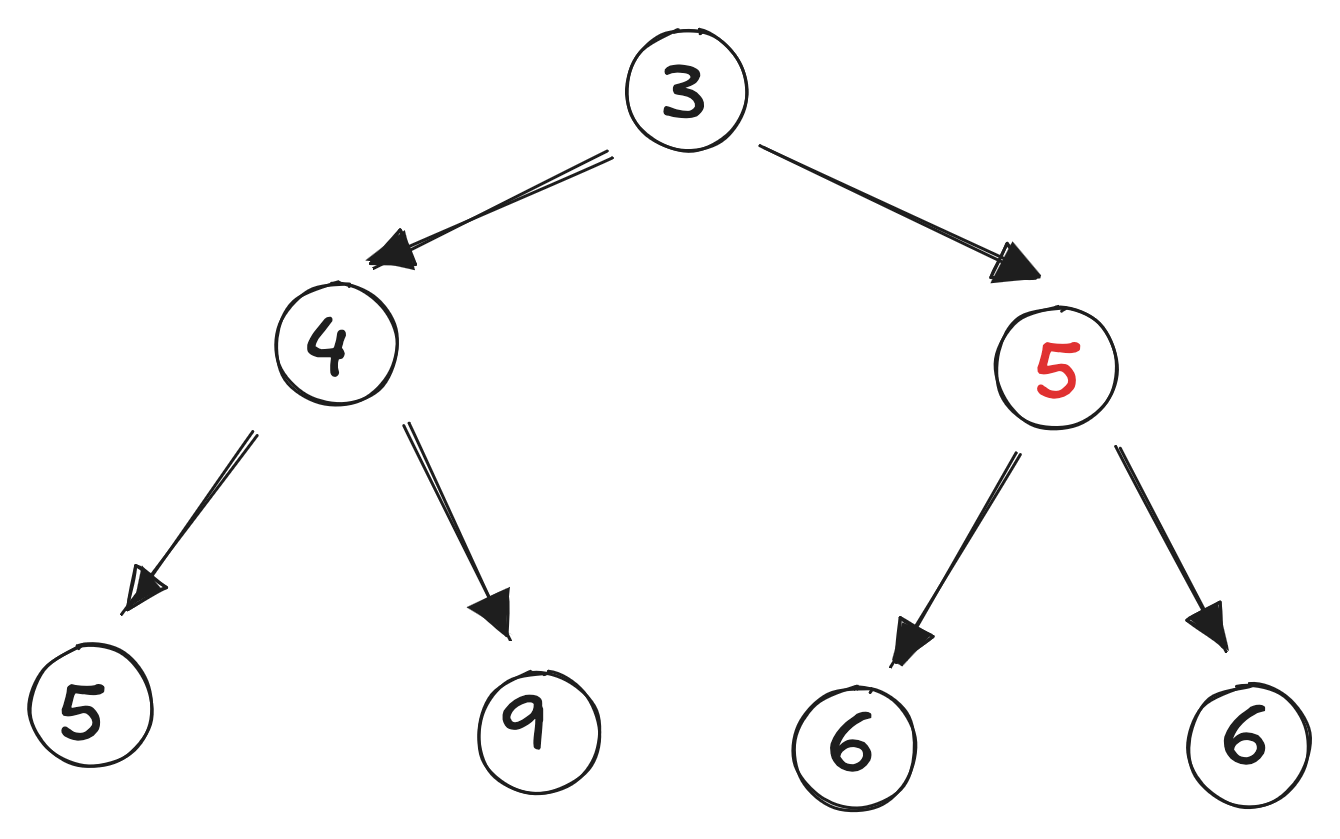
If we add another element and it’s less than it’s parent, we swap:

The new element is now in the correct position in the heap.

Heaps As Arrays

The most straightforward way to implement a binary heap is using an array. In Python, arrays use the list built-in data structure.

• This implementation takes advantage of the property of heaps that they are completely filled, left to right, at the lowest level
• The binary tree maps “linearly” to the array
• The last element (for extraction) and the next element (for addition) are very easy to find

Illustrated:

Heaps With Pointers

To implement a heap with pointers, we need to find a way to determine the next position (for insertion) and last position (for extraction) in the tree. While it is possible to keep a pointer to these nodes, it’s more straightforward to traverse the heap by keeping track of the total number of nodes in the tree.

The process for this is straightforward:

• Convert the number of nodes to binary
• Drop the leading 1
• For the remaining binary number, 0 indicates left from the root, 1 indicates right from the root

An example, finding the last node:

• The heap below has 12 elements
• 12 in binary is 0b1100
• Dropping the leading bit yields 0b100
  • The directions are 1, 0, 0 \(\rightarrow\) Right, Left, Left

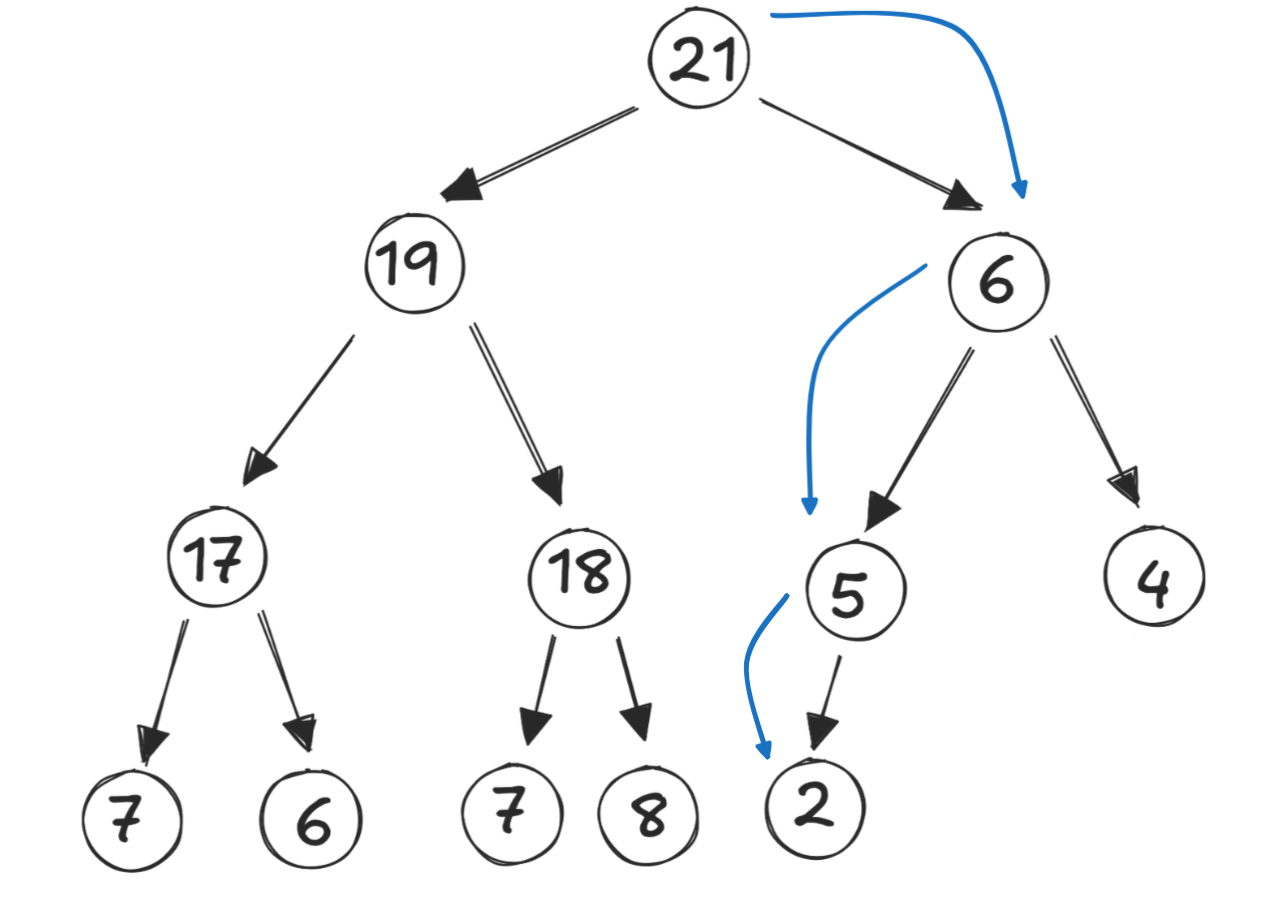
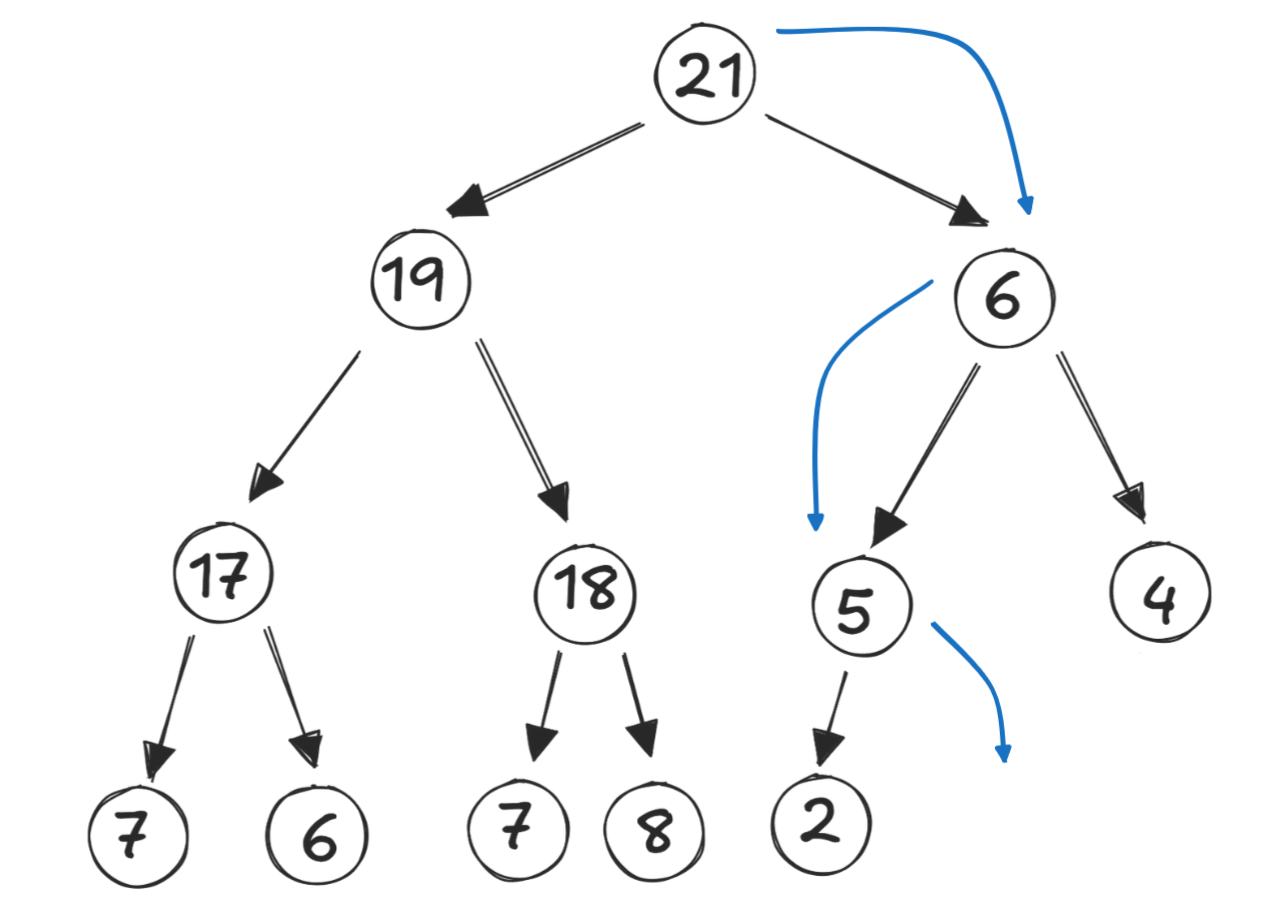
An example, finding the next position:

• The heap below has 12 elements
  • The “next” node supposes the heap has one more element: 13
• 13 in binary is 0b1101
• Dropping the leading bit yields 0b101
  • The directions are 1, 0, 1 \(\rightarrow\) Right, Left, Right

Practice

Practice Problem 11.1

Practice Problem 11.1

Modify the binary search tree from the notes so that:

• Each node has a key and a value.
• If a node is added that has a key which already exists in the tree:
  • Don’t add a new node
  • Replace the value of the existing node with that key

Practice Problem 11.2

Practice Problem 11.2

Modify the Node class to add a swap_with_parent method. You’ll need to add a parent node reference.

Homework

• Homework problems should always be your individual work. Please review the collaboration policy and ask the course staff if you have questions. Remember: Put comments at the start of each problem to tell us how you worked on it.

• Double check your file names and return values. These need to be exact matches for you to get credit.

• For this homework, don’t use any built-in functions that find maximum, find minimum, or sort. Don’t use any built-ins or libraries that implement trees or heaps.

• These problems are intended to be completed in sequence. Each builds on the previous.

For these problems, you’ll import a Node class:

node.py

class Node:
    def __init__(self):
        self.left = None
        self.right = None
        self.value = None

    def get_left(self):
        return self.left

    def get_right(self):
        return self.right

For all problems where you use nodes, you must import and extend this class.

Homework Problem 11.1

Homework Problem 11.1 (30 pts)

Implement a node-based heap storing integer values as class NodeHeap.

• Extend our Node class; import it from node.py
• The constructor should have a max keyword argument that defaults to False
  • The heap should default to a min heap
  • If max is True, the heap should be a min heap
• The constructor should accept no other arguments
  • Calling the constructor should create an empty priority queue
• Implement enqueue and dequeue methods to add and remove elements from the heap
  • The argument for enqueue should be an int
  • dequeue should return an int
• Implement a get_root method that returns a reference to the root node (without modifying the heap)

Submit as nodeheap.py.

Recall the Thing

class Thing:
    def __init__(self, a: int, b:int, c:int, d:int) -> None:
        self.a:int = a
        self.b:int = b
        self.c:int = c
        self.d:int = d

    def get_a(self) -> int:
        return self.a

    def get_b(self) -> int:
        return self.b

    def get_c(self) -> int:
        return self.c

    def get_d(self) -> int:
        return self.d

Homework Problem 11.2

Homework Problem 11.2 (40 pts)

Implement a node-based heap that stores Thing objects. You might extend your previous NodeHeap class; in any case, your nodes must extend our Node class, imported from node.py. Do this in a ThingHeap class.

• Your constructor must have a string keyword argument for key, with a default value of 'a'.
  • The key specifies which Thing value to sort by in the heap
  • The constructor should take no positional arguments, and calling it should create an empty ThingHeap
• You must implement the same enqueue, dequeue, and get_root methods as the previous NodeHeap class
  • enqueue takes one argument: a reference to a Thing
  • dequeue takes no arguments and returns a reference to a Thing

Submit as thingheap.py

Note: You will need to include a definition for the Thing class; include this class definition in thingheap.py – the only import you should need is the Node from node.py

Homework Problem 11.3

Homework Problem 11.3 (30 pts)

Implement an array-based heap, ArrayHeap, using this SimpleArray class:

simplearray.py

class SimpleArray:
    def __init__(self, L:list[int]) -> None:
        self.L:list[int] = L

    def append(self, val: int) -> None:
        self.list.append(val)

    def delete(self, index: int) -> None:
        self.list = self.list[0:index] + self.list[index+1:]

    def get(self, index: int) -> int:
        return list[index]

Use only the API provided by the class, i.e., don’t use other methods on the underlying list of the SimpleArray.

Just like your other heaps:

• The constructor should have a max keyword argument that defaults to False
  • The heap should default to a min heap
  • If max is True, the heap should be a min heap
• Implement enqueue and dequeue methods to add and remove elements from the heap
• Implement a get_array method to return a reference to the underlying SimpleArray

Submit as arrayheap.py.