Note 1: Expressions and Functions

Reading: Think Python Chapters 1, 2, 3, 6

Notes

Setup

Install Python!

The Interpreter

The interpreter lets you type in a short amount of Python code to be immediately executed. It looks like this:

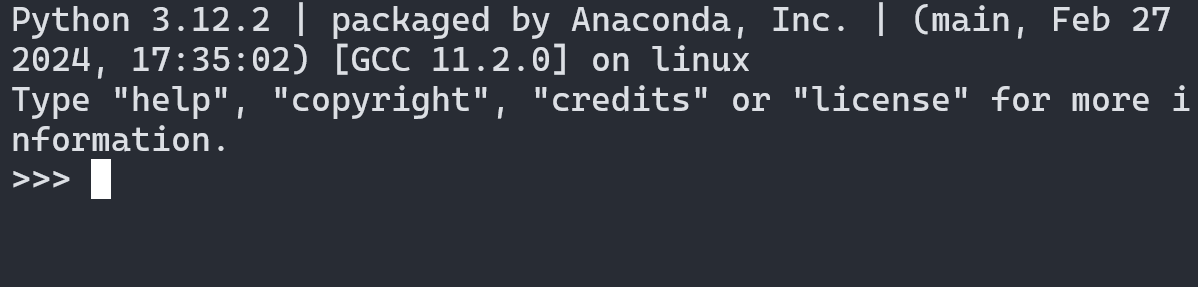
It is like a calculator, but much more powerful. Simple calculator-like math works the way you might expect.

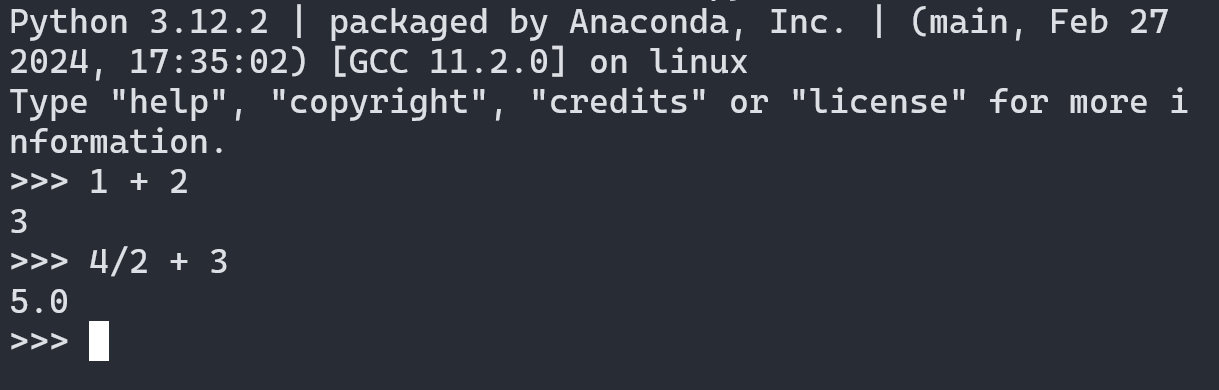
We will show Python in these notes in a similar format:

1 + 2

4/2 + 3

5.0

Math and numbers work in the interpreter, but word-like text doesn’t. Trying it will give you an error.

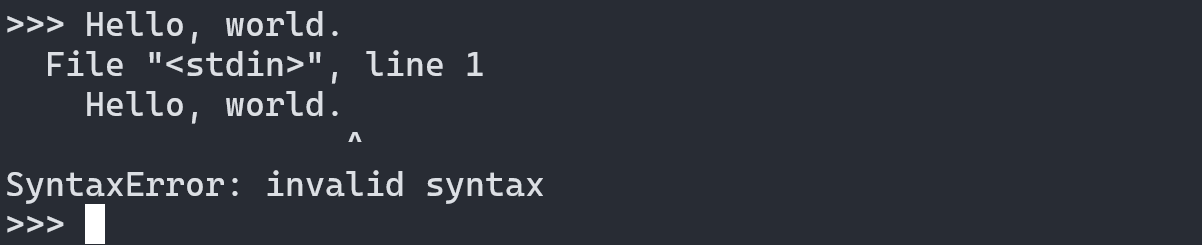
To work with text in Python, you will need to encapsulate the text in quotation marks, single, or double:

'Hello, world.'

'Hello, world.'

The interpreter always displays the result of the expression you type in (if there is no error). This is different from using a print statement.

print("Hello, world.")

Hello, world.

The difference between the string "Hello world." as an expression and the print statement print("Hello world.") is subtle when using the interpreter: quotation marks at the output.

Text Interfaces

The interpreter is a text interface to your computer. You type text, and the output displays text.

This is different from the graphical interfaces you are probably used to using, where there are buttons for you to click on, and you can drag and drop files.

Why use a text interface? It is more powerful. You can give your computer very specific instructions.

Graphical interfaces are designed to be easy to use, but they can only give the computer pre-defined instructions. If you want to solve a problem that hasn’t been solved before, you will probably need to use a text interface to succeed.

The Editor

The editor lets you write full Python programs. A program is a series of instructions that can be saved for future use. The interpreter is a great tool for experimenting, but most of your coding will be done in the editor.

An editor for Python (or any programming language) has several useful features that a normal “text editor” doesn’t have.

Syntax highlighting changes the color of the text based on what it does in the program.

Line numbers help you organize your code, and help you find and fix errors.

Running programs directly from the editor makes your life easy. There’s a way to run programs from outside the editor, too, but we will save that for later.

Here is an example of a short Python program written in VSCode:

Visual Studio Code:

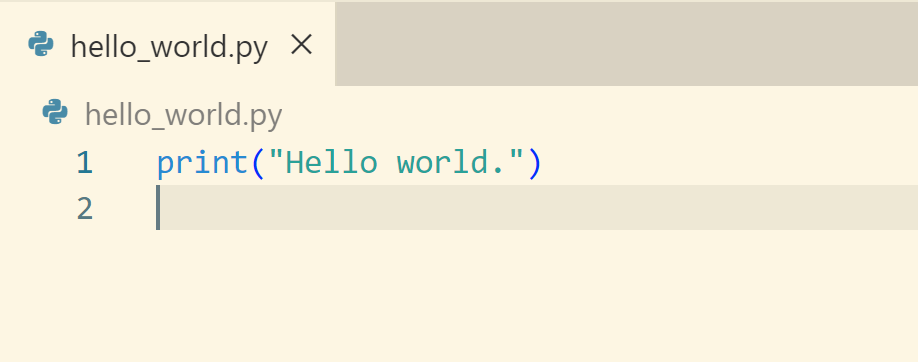
When you run this program, you’ll get printed output displayed at the terminal/shell:

Hello, world.

An important note: Python programs (not in the interpreter) only result in printed output when we instruct them to print with a print statement.

Here’s a program with just an expression, and no print statement:

The program will run with no errors, but there will be no printed output.

Comments

A Python program consists of logical instructions for the programming language to execute. Sometimes, however, we want to include English (or other natural language) text for human beings to read.

We include this text in comments:

Comments start with a pound sign #.
Comments can be an entire line (if the # starts the line)
Comments can be inline (if the # comes after some valid code).

comments.py

print("Hello")
# this is a comment, it doesn't change how the code runs
print("world.") # this is also a comment

Arithmetic

The Python interpreter is much more than a calculator. We can see how it works by looking at some elementary math.

Consider the mathematical expression \((4 + 2) \times 3\). We can express this in Python in a very similar way:

(4 + 2) * 3

The parentheses are important, without them, we would be evaluating a different operation:

4 + 2 * 3

In the conventional order of operations, multiplication occurs before addition. Without the parentheses, Python firsts evaluates the simple expression 2 * 3:

2 * 3

and then ‘replaces’ that expression with its result before evaluating the next expression:

4 + 6

By adding the parentheses, we tell Python to evaluate the expression inside the parentheses first, and then replace that expression with its result.

6 * 3

You will never explicitly see a sub-expression replaced by its result. This only happens “under the hood” when Python runs your code. However, you can always try out sub-expressions using the interpreter to make sure your code is doing what you want it to do.

Remember: when in doubt, use parentheses to explicitly instruct Python the order for evaluating expressions. You will end up using parentheses for much more than just simple math.

Operators

A basic way to craft expressions in Python is with operators. Many operators look and behave (almost) the same way in Python as they do in math.

Operator	Function (with numbers)
`+`	Addition
`-`	Subtraction
`*`	Multiplication
`/`	Division
`**`	Exponentiation
`//`	Quotient
`%`	Remainder

You should know how these operators work with numbers. They will work differently (or not work at all) with other kinds of data, which we will see later. For exams in the class, you will never need to do anything more than basic arithmetic and counting.

Whitespace

“Whitespace” refers to characters in a text (or .py) file that appear to be blank, such as spaces, tabs, and carriage returns.
Whitespace is important in Python, because it separates different logical operations
- Carriage return (“enter”) ends a logical line
- Additional spaces are usually optional if there is no ambiguity
- Tabs organize and associate code (you will see this later)

These expressions are equivalent:

2+4*(3+1)

2 + 4 * (3 + 1)

Python does not care if your code is easy for humans to read, but you should care. The code below will run, but you should avoid inconsistent spacing, because it makes the code difficult to read. If you start working on a problem, stop, and come back to it later, you will want to be able to read your own code.

2+ 4    * ( 3 +1        )

Text

In Python, by placing characters (including numbers) between quotation marks, we form strings, text data. You can use single or double quotation marks, but they must match.

Both of these will work:

"Hello!"

'Hello!'

'Hi.'

'Hi.'

But this gives us an error:

"Hello'

We can use some mathematical operators with strings, but the behavior may not be intuitive. Strings are not numbers.

For now, let’s use the + operator. It concatenates (attaches end-to-end) two strings.

'view' + "point"

'viewpoint'

Wrapping numeric characters with quotation marks means those numbers are interpreted as text:

'1' + "2"

'12'

Mixing numbers and strings with the + operator will give you an error.

1 + "2"

Printing

Remember that while the interpreter will always show you the result of an expression, you need to use print statements for your programs (in the editor) to have any output.

concatenate_print.py

print("1" + "2")
print("three")

Whatever is inside the parentheses of the print function will be evaluated, and the result will be printed to the console. The expression (or value) inside the print statement does not need to result in (or be) a string!

add_print.py

print(1 + 2)
print(3)

Notice that after each print statement, the next print statement appears on a new line.

Variables

The result of an expression can be assigned to a variable for later use.

x = 3 + 1

Variable x has been assigned the value 4. When we reference x in an expression, that value is retrieved:

print(x)

The assignment operator = is not the same as mathematical equality. It works like this:

The expression to the right of the = is evaluated
After evaluation, the result is assigned to the variable left of the =

This means that we can write Python code that doesn’t translate directly to a math equation:

x = 3 + 1

3 + 1 was evaluated and x was assigned 4.

x = x + 1

x + 1 was evaluated: x was 4, so x + 1 became 4 + 1. After evaluation, x was assigned 5.

print(x)

The idea of variables having different values at different times during program execution is called state. In the interpreter, state is maintained (variable names are saved) until you change them with a new assignment, or you restart the interpreter. When running a program you write in the editor, state is reset each time you run the program.

Variables do not exist until you first assign them. Referencing a variable you haven’t assigned will yield an error:

print(y)

Variable names are text, but they are not interpreted as text. However, if you put a variable name in between quotation marks, that tells Python to interpret the name literally, as a string, with no connection to the variable.

print('y')

Not all ‘names’ are valid for variables: the textbook goes into more detail. In general, start variable names with a letter.

This is a place that whitespace is important: the space after a variable name indicates the end of the name. This means you cannot have a space in the name. To get around this, use underscores:

coffee type = 'espresso'

coffee_type = 'espresso'

Function Calls

Functions are pre-defined sequences of instructions. Like variables, functions have names, and functions must adhere to the same naming convention. We can call a function with the following syntax:

function_name()

The function’s name is spelled out
A set of parentheses comes immediately after the function name
- Values placed in the parentheses, called arguments, modify what the function does
After the function call finishes, the function call is replaced with a return value
- Not all functions have a return value
- If there is no return value, then a special object None is returned

Unless you define a function called function_name() when you run the code above, you’ll get an error.

Functions can form parts of expressions:

int('25') + 2

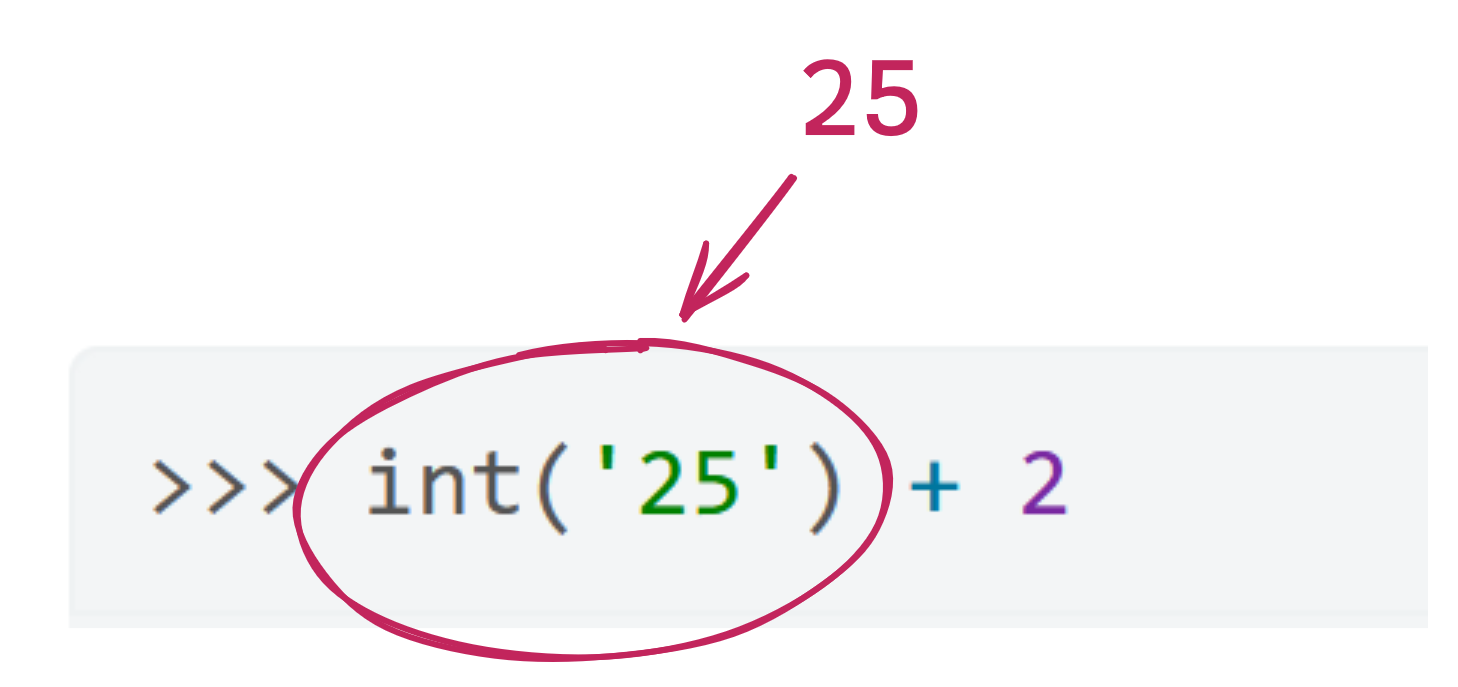
Since int('25') returns the integer 25, after the function call, this is equivalent to:

25 + 2

Expressions can form the arguments of function calls:

int('2' + '5') + 2

The expression '2' + '5' is evaluated before the function call. It is inside the parentheses of the call, and function call parentheses respect order just as expression parentheses do.

'2' + '5'

'25'

After the evaluation, the result becomes int('25') + 2, identical to the first example. As always, these intermediate steps will never be shown to us by Python, but it’s important to understand how the programming language works.

There is no limit to how deep you can nest function calls and expressions:

str(int('2' + '5') + 2) + "3"

'273'

In practice, however, writing and reading this sort of deeply-nested function call is difficult, and unnecessary. Instead, use variables:

first = '2' + '5'

second = int(first) + 2

third = str(second) + "3"

print(third)

Math

Python comes with a built-in module, math, for simple mathematical functions. The module comes with functions and variables.

To import a module, use the import keyword, followed by a space, followed by the module name:

import math

You only need to do this once in the interpreter, or once at the beginning of a program you write in the editor.

After importing the module, you can use its functions:

math.ceil(2.1) # math.ceil returns the next largest integer

math.floor(1.99) # math.floor returns the next smallest integer

Note the syntax: there is a dot in between the module name math and the name of the function: this indicates to Python that the function is associated with the module.

Modules can also include variables; one example from math is math.pi, a good approximation of \(\pi\):

math.pi

3.141592653589793

Composition

Like everything you’ve seen so far, these functions and variables can be composed into expressions. We’ll start with a simple expression:

math.pi/2

1.5707963267948966

This expression can form the argument of a function:

math.ceil(math.pi/2)

That expression can be combined with other functions or operators into a more complicated expression:

math.ceil(math.pi/2) + math.floor(3 + int('1'))

There’s no technical limit to how complicated this can get:

str(math.ceil(math.pi/2) + math.floor(3 + int('1'))) + " is the result"

'6 is the result'

There is almost never a need to make an expression as complicated as the one above.

Here is the same result composed with variables. This is easier to do using the editor than the interpreter. It uses more lines of code, but achieves the same result.

equivalent.py

import math
a = math.pi/2
b = math.ceil(a)
c = int('1')
d = 3 + c
e = math.floor(d)
f = b + e
g = str(f)
h = g + " is the result"
print(h)

Tracing With The Visualizer

For important examples, you can trace through (and edit) the code directly within these course notes.

Note that the program written in the editor requires a print statement to have output:

Python programs (written in the editor) only print to the console when specifically instructed to
Python expressions evaluated in the interpreter will display the result of the expression

Defining Functions

Beyond built-in functions and functions from modules, Python lets us define our own functions. This allows us to write code once and execute it many times.

simple_function.py

def hello_world():
    print("Hello, world.")

The function definition introduces new syntax:

The keyword def (“define”)
The function name with a colon (:) afterwards
An indented code block

You will see many more examples of this kind of syntax, with a controlling statement, a colon, and an indented block. The indentation groups a block of code with the controlling statement. It says that everything indented belongs to, and is controlled by, the function definition (in this case).

If we run the simple_function.py program above (try it), there will be no output. We have defined the function, but we have not called it.

Calling a user-defined function is the same as calling a built-in function: use the function name, followed by parentheses.

simple_function_call.py

def hello_world():
    print("Hello, world.")

hello_world()

Hello, world.

Note that the function call occurs outside of the indented block of the function definition, and remember that while the function definition does not do anything by itself, you must define a function before using it (if it isn’t a built-in function like str() or print()).

Return values and `None`

We haven’t specified a return value for the function, so it returns nothing. In Python, “nothing” is represented by a special variable called None. It isn’t zero, it isn’t the string 'None', it’s nothing.

Trace the execution of this program:

simple_function_call.py

def hello_world():
    print("Hello, world.")

i = int(40.1)
print(i)
j = hello_world()
print(j)

Three things are printed because there are three print statements:

The function definition is read
The expression to the right of the = on line 4 is evaluated
- int(40.1) returns int 40
- The result is assigned to i
First print: i is printed
The expression to the right of the = on line 6 is evaluated
- This is a function call to hello_world()
- Second print: 'Hello, world.' is printed by the function call
- The function returns nothing: None
- The expression result, None, is assigned to j
- Third print: j is printed

Fundamentals

Trace through this program, modify it, understand it. Ask questions if you have them.

It’s a short program, but it demonstrates several concepts that are fundamental to what we will learn in the future.

print() is a built-in function that returns None in addition to creating output at the console.

To demonstrate, let’s assign the return from print to a variable:

a = print("Something")

Something

The print statement still creates the output we expected. If we print what was returned:

print(a)

None

Parameters and Arguments

We have called built-in functions with arguments, such as int(40.1). We can also define functions that take arguments:

simple_function_call.py

def rounder(v):
    str_v = str(v)
    rounded_v = int(v)
    rounded_str = str(rounded_v)
    print(str_v + " rounds to " + rounded_str)
rounder(5.2)
rounder(4.6)

Trace through the execution. Note how variable v is internal to the rounder function. Each time the function is called, \(v\) takes a different value.

Defining your own functions, especially functions that take arguments, is a powerful part of code reuse. Code reuse makes programming extremely powerful: you can write instructions once, and execute them many times, running them with different inputs to get different outputs.

Function `return`

We have seen built-in functions that return a value after evaluation, such as float:

x = float(3)

print(x)

3.0

We have also seen how print does not return anything (None):

y = print("this gets printed")

this gets printed

print(y)

None

We have also written our own functions, so far without returning anything:

def print_cube(in_value):
    print(in_value * in_value * in_value)

Calling the function results in the print statement running (and printed output). However, nothing is returned.

Defining `return` Values

We can write functions so that they do return something. This is one of the most powerful concepts in computer programming.

To make your function return a value, use the keyword return at the end of the function:

function_return.py

def return_double(x):
    y = 2 * x
    return y

d = return_double(3)
print(d)

When execution inside a function reaches a return statement:

Execution inside that function ends
The return value is brought back to the function call
- The value “replaces” the function call
- This is similar to evaluation of an expression

Note that nothing is printed by the function itself!

The function call on line 5 results in a value being returned and assigned to d
There is only printed output from the explicit call to print on line 6

Multiple Function Arguments

A function can have any number of arguments. We’ve defined functions with no arguments and one argument. Multiple arguments are similar:

multiple_args.py

def smaller(a, b):
    if a < b:
        return a
    elif b < a:
        return b
    else:
        return a

x = smaller(3, 4)
print(x)

Arguments are passed into the function in the same position as the function call. Since 3 is the first argument, it becomes a when the function is called; likewise 4 becomes b.

Remember: if you define a function as needing a certain number of arguments, it must be called with that number of arguments. Otherwise, you’ll get an error.

Practice

Practice Problem 1.1

Rewrite the program below:

Combine the expressions on lines 1-3 into a single expression on one line
- The expression should yield the same result and assign to variable z
Keep the print(z) to check the output

practice1_3_1.py

x = 3.5
y = int(x) + 1
z = str(y) + "2"
print(z)

Practice Problem 1.2

Rewrite the expression below with several intermediate variables. Keep the print statement to check your work.

practice1_3_2.py

result = float(str(int("3") + 2.5))/2 + 1
print(result)

Practice Problem 1.3

The program below is meant to add up the integers between 1 and 5, take the square root of the result:

\(x = 1 + 2 + 3 + 4 + 5\)

\(y = \sqrt(x)\)

…and then print the square root. The program has an error. Fix it!

practice1_3_3.py

x = 1 + 2 + 3 + 4 + 5
y = math.sqrt(x)
print(y)

Practice Problem 1.4

Write a function fixed_sequence that takes no arguments and prints the following when called:

1 2 3 4

Begin with this “starter code.”

practice1_3_4.py

def fixed_sequence(): # function definition
    # write the body of the function here

fixed_sequence() # keep these two function calls
fixed_sequence()

Keep the two function calls: when you have written the body correctly, the program should print:

1 2 3 4
1 2 3 4

Practice Problem 1.5

Write a function variable_sequence that takes one argument, an integer, and prints out that integer and the next three consecutive integers in sequence:

variable_sequence(1) results in printed 1 2 3 4
variable_sequence(2) results in printed 2 3 4 5
variable_sequence(4) results in printed 4 5 6 7

Begin with this “starter code.”

practice1_3_5.py

def variable_sequence(first): # function definition
    # write the body of the function here

variable_sequence(1) # keep these three function calls
variable_sequence(2)
variable_sequence(4)

Keep the function calls: when you have written the body correctly, the program should print:

1 2 3 4
2 3 4 5
4 5 6 7

Practice Problem 1.6

Write a function return_sequence that takes one argument, an integer, and returns a string consisting of that integer and the next three consecutive integers in sequence:

return_sequence(1) results in returned string '1 2 3 4'
return_sequence(2) results in returned string '2 3 4 5'
return_sequence(4) results in returned string '4 5 6 7'

Homework

Homework problems should always be your individual work. Please review the collaboration policy and ask the course staff if you have questions. Remember: Put comments at the start of each problem to tell us how you worked on it.
Double check your file names and printed output. These need to be exact matches for you to get credit.

Homework Problem 1.1

Homework Problem 1.1 (20 pts)

Write a function squared_root that takes one argument, an integer, and prints out that integer, its square root, and its square, and the integer again, in sequence, with a single space in between each:

squared_root(1) results in printed 1 1 1 1
squared_root(4) results in printed 4 2 16 4
squared_root(0) results in printed 0 0 0 0

You can expect the argument will always be positive integer that is a perfect square.

Begin with this “starter code.”

squared_root.py

# any initial comments go here
def squared_root(input_int):
    # write the body of the function here

squared_root(1)
squared_root(4)
squared_root(0)

Once the function is working, remove the function calls, and keep only the function definition. Submit as squared_root.py.

Hint: You can use the str() function to convert any numeric value into a string, and the + operator between strings to concatenate (join) them.

Homework Problem 1.2

Homework Problem 1.2 (20 pts)

The program below is intended to implement the reverse_sequence function:

The function should take one argument, an integer
The function should print out a sequence of four integers:
- The sequence starts with the argument
- Each successive number is two less than the previous number
There is a single space in between each number
reverse_sequence(6) should print 6 4 2 0
reverse_sequence(3) should print 3 1 -1 -3

reverse_sqeuence.py

# initial comments
def reverse_sequence(initial):
    second = initial - 2
    third = second - 2
    fourth = third - 4
    print(initial + second + third + fourth)

Fix/complete the function so that it works as intended. Submit as reverse_sequence.py.

Homework Problem 1.3

Homework Problem 1.3 (20 pts)

This program will contain two functions.

Write one function, hello_world that simply prints Hello, world!.

Write a second function, call_hello_world that contains a function call to the first hello_world function.

call_hello_world.py

# initial comments
def hello_world():
    # complete the function

def call_hello_world():
    # complete the function

call_hello_world() # this line tests your code, delete before submitting

When finished:

The function call at the end of the program should result in printed output Hello, world!
Changing the printing in the first function (hello_world) should change the output of the call to the second function
- This is because the second function calls the first function

Before submitting, delete the call to call_hello_world. Keep the definitions. Submit as call_hello_world.py.

Homework Problem 1.4

Homework Problem 1.4 (20 pts)

Write a function time_convert that converts from seconds to days. It should truncate at five digits after the decimal. Output should print in the following format:

time_convert(500) prints 500 seconds is 0.00578 days
time_convert(2000) prints 2000 seconds is 0.02314 days

Submit as time_convert.py

Hint

There are 60 seconds in one minute. There are 60 minutes in one hour. There are 24 hours in one day.

You can truncate by:

Multiplying by a factor of ten
Calling math.floor on the result
Dividing that result by the same factor of ten

The factor of ten you choose (10, 100, 1000, etc.) will determine the decimal place of the truncation.

Homework Problem 1.5

Homework Problem 1.5 (20 pts)

Write a function time_convert_return that performs the same conversion as the previous problem, but instead of printing the output, it returns a string:

time_convert_return(500) returns string '500 seconds is 0.00578 days'
time_convert_return(2000) returns string '2000 seconds is 0.02314 days'

Submit as time_convert_return.py

Hint

There are 60 seconds in one minute. There are 60 minutes in one hour. There are 24 hours in one day.

You can truncate by:

Multiplying by a factor of ten
Calling math.floor on the result
Dividing that result by the same factor of ten

The factor of ten you choose (10, 100, 1000, etc.) will determine the decimal place of the truncation.

Notes

Setup

The Interpreter

The Editor

Comments

Arithmetic

Operators

Whitespace

Text

Printing

Variables

Function Calls

Math

Composition

Defining Functions

Return values and None

Parameters and Arguments

Function return

Defining return Values

Multiple Function Arguments

Practice

Practice Problem 1.1

Practice Problem 1.2

Practice Problem 1.3

Practice Problem 1.4

Practice Problem 1.5

Practice Problem 1.6

Homework

Homework Problem 1.1

Homework Problem 1.2

Homework Problem 1.3

Homework Problem 1.4

Homework Problem 1.5

Return values and `None`

Function `return`

Defining `return` Values