\( \newcommand{\blah}{blah-blah-blah} \newcommand{\eqb}[1]{\begin{eqnarray*}#1\end{eqnarray*}} \newcommand{\eqbn}[1]{\begin{eqnarray}#1\end{eqnarray}} \newcommand{\bb}[1]{\mathbf{#1}} \newcommand{\mat}[1]{\begin{bmatrix}#1\end{bmatrix}} \newcommand{\nchoose}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array}\right)} \newcommand{\defn}{\stackrel{\vartriangle}{=}} \newcommand{\rvectwo}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array}\right)} \newcommand{\rvecthree}[3]{\left(\begin{array}{r} #1 \\ #2\\ #3\end{array}\right)} \newcommand{\rvecdots}[3]{\left(\begin{array}{r} #1 \\ #2\\ \vdots\\ #3\end{array}\right)} \newcommand{\vectwo}[2]{\left[\begin{array}{r} #1\\#2\end{array}\right]} \newcommand{\vecthree}[3]{\left[\begin{array}{r} #1 \\ #2\\ #3\end{array}\right]} \newcommand{\vecfour}[4]{\left[\begin{array}{r} #1 \\ #2\\ #3\\ #4\end{array}\right]} \newcommand{\vecdots}[3]{\left[\begin{array}{r} #1 \\ #2\\ \vdots\\ #3\end{array}\right]} \newcommand{\eql}{\;\; = \;\;} \definecolor{dkblue}{RGB}{0,0,120} \definecolor{dkred}{RGB}{120,0,0} \definecolor{dkgreen}{RGB}{0,120,0} \newcommand{\bigsp}{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \newcommand{\plss}{\;\;+\;\;} \newcommand{\miss}{\;\;-\;\;} \newcommand{\implies}{\Rightarrow\;\;\;\;\;\;\;\;\;\;\;\;} \)

Review: Part II

Part I    Part III

r.5    Matrix-matrix multiplication and what it means

 

Multiplying one matrix by another produces a matrix, but why is that and what good is it?

There are generally four contexts where we see matrix-matrix multiplication:

Before proceeding, let's address multiply-compatibility for matrix-matrix and matrix-vector multiplication:

 

Let's start with the first context:

 

When we work out the algebra, it turns out that there are two useful ways of describing matrix-matrix multiplication:

 

Let's look at cases where the second context arose:

 

Next, let's say a few things about matrix inverses:

 

Finally, let's look at the fourth context: matrix-multiplication as a "matrix transformer"

  • There are three types of row operations:
    1. Scale: divide one row by a number (like we did above) $$ {\bf r}_i \leftarrow \frac{{\bf r}_i}{\alpha} $$
    2. Swap: swap two rows $$\eqb{ {\bf\mbox{temp}} & \leftarrow &{\bf r}_i\\ {\bf r}_i & \leftarrow & {\bf r}_j\\ {\bf r}_j & \leftarrow & {\bf\mbox{temp}} }$$
    3. Replace a row by adding a multiple of another row. $$ {\bf r}_i \leftarrow {\bf r}_i + \alpha {\bf r}_j $$
    You could devise others but these are enough.

  • There is also an order in which we change coefficients:
    • Always start with row 1, column 1, trying to make that element a pivot.
    • When we're successful making an element into a pivot, we change coefficients below the pivot to zero.
    • The search for the next pivot moves to the next row, next column.
    • A search may not be successful, in which case we move to the next column (same row).
    • After the final pivot we go back to the first one and start the process of creating zeroes above each pivot.

  • Here's what we get after making zeroes below the first pivot:

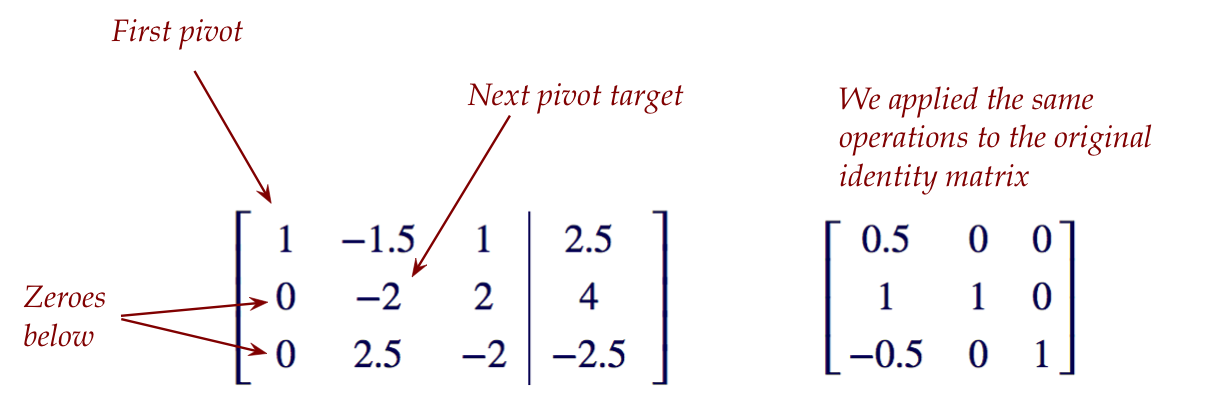
  • Continuing in this manner, we get the RREF (and by its side, if the RREF is full-rank, the inverse): $$ \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 2\\ 0 & 1 & 0 & 3\\ 0 & 0 & 1 & 5 \end{array} \right] \;\;\;\;\;\;\;\;\;\;\;\; \mat{-0.5 & 0.5 & 1 \\ 1 & 2 & 2 \\ 1.5 & 2.5 & 2} $$ What we see:
    • A full-rank RREF (a pivot in every column), which tells us the equations have a unique solution.
    • Notice: the non-augmented part of the full-rank RREF is the identity matrix of that size.
    • The solution itself is in the augmented column: \(x_1=2, x_2=3, x_3=5\)
    • We know this is the solution because we can convert back to equations by looking at $$ \left[ \begin{array}{ccc|c} 1 & 0 & 0 & 2\\ 0 & 1 & 0 & 3\\ 0 & 0 & 1 & 5 \end{array} \right] $$
    • We get the inverse matrix on the right. $$ {\bf A}^{-1} \eql \mat{-0.5 & 0.5 & 1 \\ 1 & 2 & 2 \\ 1.5 & 2.5 & 2} $$

  • So now let's turn to: why does this work?
    • Clearly, manipulating the augmented matrix is the same thing as manipulating the coefficients of the equations.
    • So, if we end up with a full-rank RREF we know we just have a different version of the same equations with the same solution as the original.
    • Seeing that the right-side matrix is the inverse needs some reasoning.

  • Consider the starting non-augmented matrix for the equations example we've seen: $$ {\bf A} \eql \mat{ 2 & -3 & 2 \\ -2 & 1 & 0 \\ 1 & 1 & -1} $$
    • Define the matrix $$ {\bf R}_1 \eql \mat{0.5 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1} $$
    • Left-multiply \({\bf A}\) by \({\bf R}_1\) : $$ {\bf R}_1 {\bf A} \eql \mat{0.5 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1} \mat{ 2 & -3 & 2 \\ -2 & 1 & 0 \\ 1 & 1 & -1} \eql \mat{ 1 & -1.5 & 1 \\ -2 & 1 & 0 \\ 1 & 1 & -1} $$
    • This shows that multiplication by \({\bf R}_1\) achieves "multiply first row by 0.5" (or divide it by 2, which is what we seek).
    • In this way, \({\bf R}_1\) transforms \({\bf A}\) into another matrix (making a pivot, which was our goal).

  • As we've seen all three types of row operations can be achieved by a matrix multiplication that "transforms".

  • So, when we get an RREF at the end of \(k\) row operations (transformations) we can describe it as: $$ \mbox{RREF}({\bf A}) \eql {\bf R}_k {\bf R}_{k-1} \ldots {\bf R}_2 {\bf R}_1 {\bf A} $$ where the first row op is acheived by \({\bf R}_1\), the second is represented by \({\bf R}_2\) applied to the result, and so on.

  • Recall: we applied these exact same transformations to the identity matrix (in parallel, on the right side of our long list of row ops).
    • So, the question is: what do we get when applying $$ {\bf R}_k {\bf R}_{k-1} \ldots {\bf R}_2 {\bf R}_1 {\bf I} \eql ? $$
    • Let's go back to $$ \mbox{RREF}({\bf A}) \eql {\bf R}_k {\bf R}_{k-1} \ldots {\bf R}_2 {\bf R}_1 {\bf A} $$ and do two things:
      1. Recognize that \( \mbox{RREF}({\bf A}) = {\bf I}\)
      2. Multiply all the \({\bf R}_i\) matrices into one matrix: $$ {\bf R} \defn {\bf R}_k {\bf R}_{k-1} \ldots {\bf R}_2 {\bf R}_1 $$
    • Then, the reduction to RREF can be written as: $$ {\bf I} \eql {\bf R} {\bf A} $$ which means that \({\bf R}\) is the inverse of \({\bf A}\)!

  • Now, we don't actually maintain the products of row operations for the sake of separately computing \({\bf R}\).
    • Instead, we applied all the row ops to \({\bf I}\): $$ {\bf R} {\bf I} $$
    • But this results in $$ {\bf R} {\bf I} \eql {\bf R} $$

  • So, the result at the end on the right side is the inverse of \({\bf A}\) because \({\bf R}={\bf A}^{-1}\).
     

    One last point: if we've already solved for the variables, why do we need the inverse?

    • Let's state this question as follows:
      • We started with wanting to solve \({\bf Ax}={\bf b}\) for some \({\bf A}\) and some \({\bf b}\), the given equations.
      • We applied row reductions to get \(\mbox{RREF}({\bf A})\).
      • That gave us the solution \({\bf x}\).
      • Isn't that enough? Why also compute \({\bf A}^{-1}\) on the right side?

    • In applications, it turns out that very often the equations stay the same but the right side changes to \({\bf Ax}={\bf c}\)
      • In this case, we solve once to get \({\bf A}^{-1}\) and apply it to a new right side: $$ {\bf x} \eql {\bf A}^{-1} {\bf c} $$

    • In other applications like least-squares, we need to compute the inverse of matrices like \(({\bf A}^T{\bf A})\).

    • In fact, in general, linear algebra applications usually care more about inverses than solving equations.
     

    r.6    Spaces, span, independence, basis

     

    Let's consider span first:

    • We'll do this by example.

    • Consider the 3D vectors $$ {\bf u} \eql \vecthree{4}{0}{2} \;\;\;\;\;\;\;\; {\bf v} \eql \vecthree{0}{5}{3} $$

    • The span is all the vectors you can get by linear combinations, which we formally write as: $$ \mbox{span}({\bf u,v}) \eql \{{\bf z}: {\bf z} = \alpha{\bf u} + \beta{\bf v}, \mbox{ for some } \alpha,\beta\} $$ How to read aloud: "all z such that z can be expressed as a linear combination of u and v"

    • These are 3D vectors, so what does the span look like? Let's draw some vectors in the span:

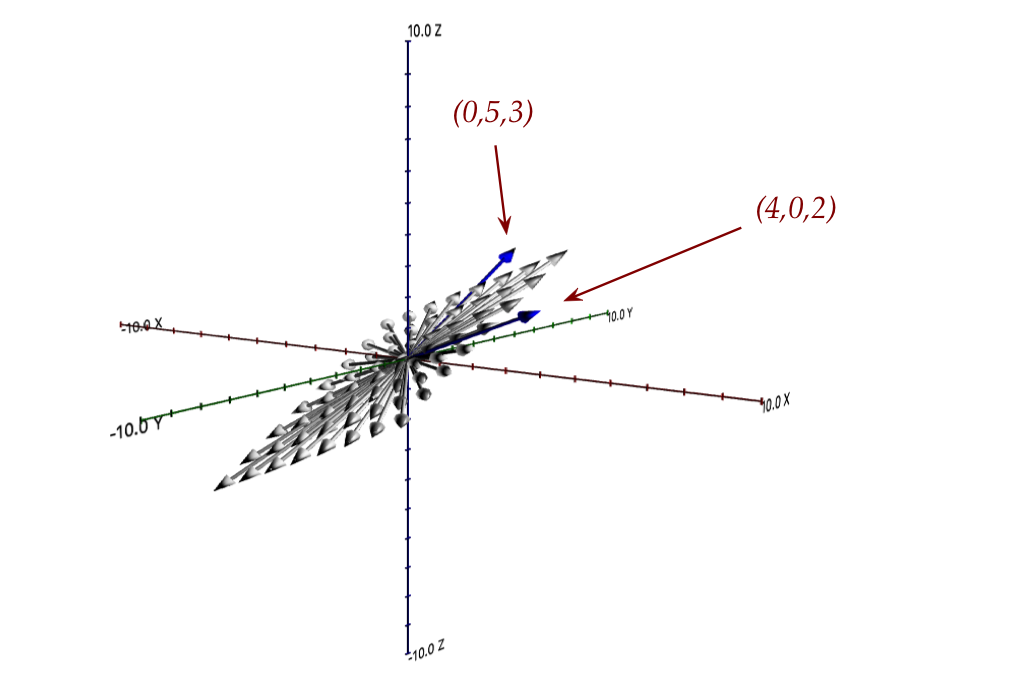
      • All the vectors in the span lie in the plane containing \({\bf u}\) and \({\bf v}\).
      • The vector \((0,0,10)\), for example, which runs along the z-axis is not in the span.

    • Now look at the plane above and ask: is there any vector in that plane that's not in \(\mbox{span}({\bf u,v})\)?
      • No, because we can surely find a linear combination to reach it.

    • Now for another important question: pick any three vectors in that plane, and call them \({\bf x,y,z}\)

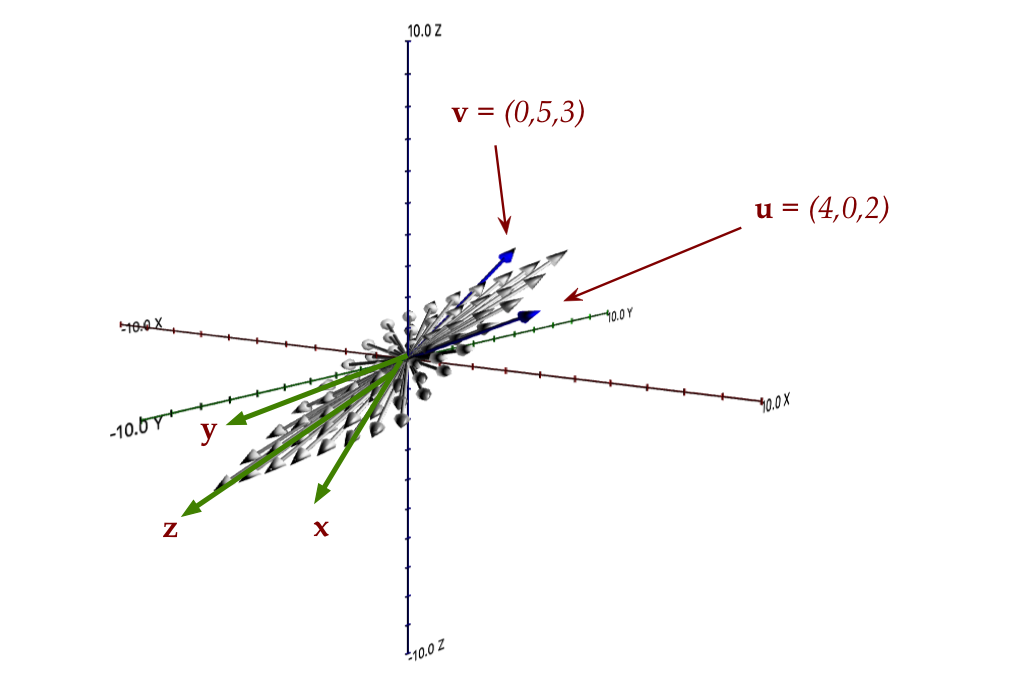
      • Is every linear combination of these three in the same plane?
      • It seems obvious that the answer is yes because all their parallelograms will lie in the plane.

    • The implication is that the plane shown above is "complete" in that it contains all linear combinations of any subset of vectors.
      • Such a collection is called a subspace.
      • More formally: a subspace is a collection of vectors where the linear combination of any two vectors is in the collection.

    • Now consider the vectors \({\bf y}\) and \({\bf w}\) in this picture:

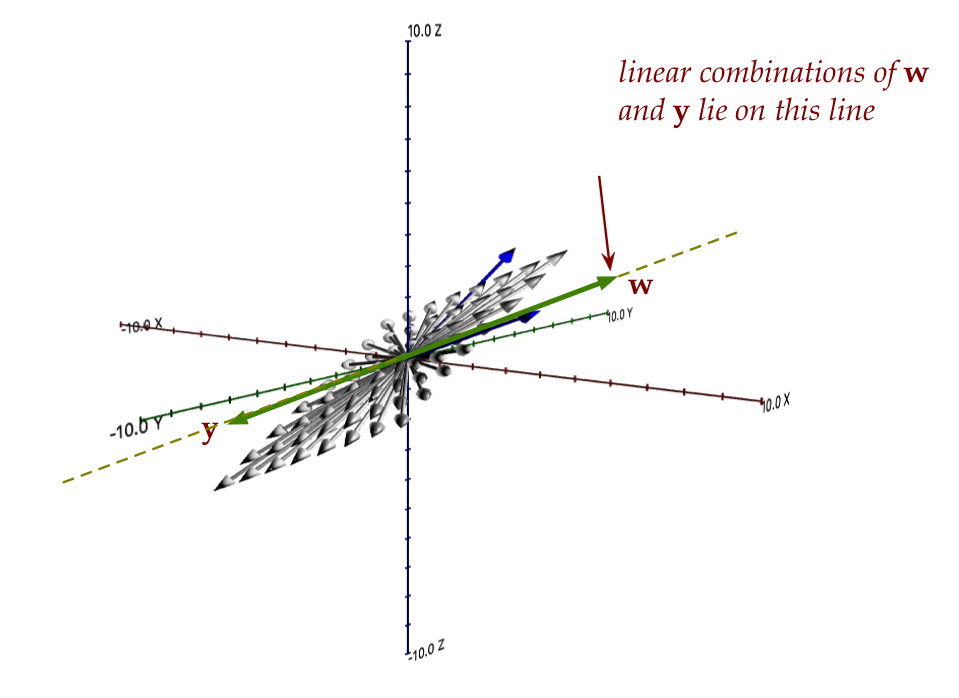
      • Clearly all linear combinations of the two lie on the dotted line, and so these two cannot linearly generate every vector in the grey plane.
      • The question we ask is: what is the minimum number of vectors needed to span the grey plane?
      • The answer is: two
      • These could be any two non-collinear (independent!) vectors like \({\bf u}\) and \({\bf v}\):

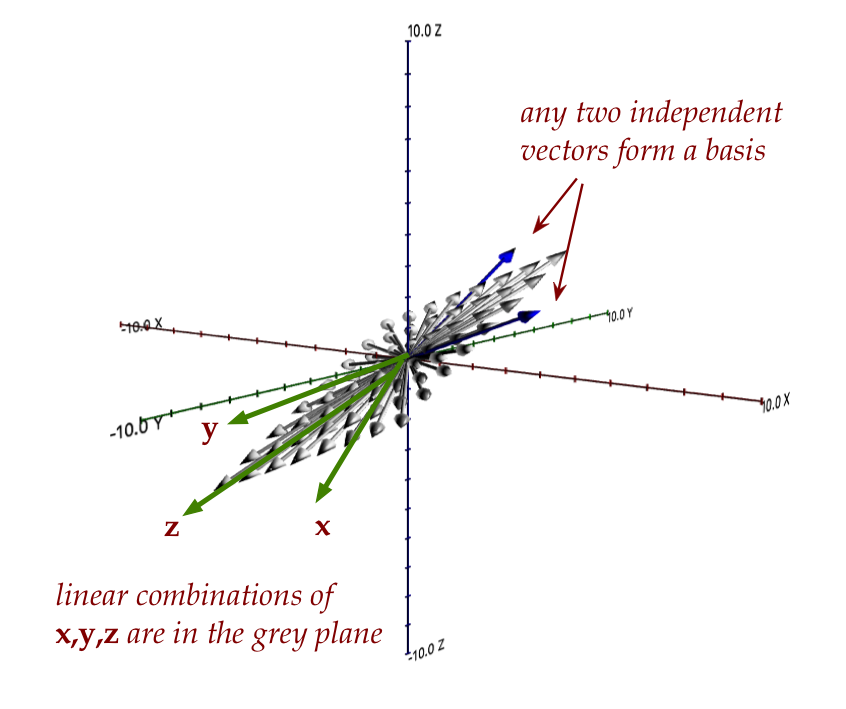
    • We are led to the definition of a basis:
      • A basis for a subspace is any minimal collection of vectors whose span is the subspace.
      • Observe: two vectors are not enough for all of 3D space.
      • Could \({\bf u}\), \({\bf v}\) and \({\bf y}\) be a basis for all of 3D space?
      • A basis for 3D space needs three, and three that are not co-planar (in the same plane).

    • We are often interested in an orthogonal basis:
      • Are \({\bf u}\) and \({\bf v}\) orthogonal?
      • Let's check: $$ {\bf u} \cdot {\bf v} \eql (4,0,2) \cdot (0,5,3) \eql 6 \neq 0 $$ So, no, they are not orthogonal and thus even though \({\bf u}\) and \({\bf v}\) are a basis, they are not an orthogonal basis.
      • Consider \({\bf u}=(4,0,2)\) and \({\bf r}=(3,-\frac{25}{2}, -6))\) $$ {\bf u} \cdot {\bf r} \eql (4,0,2) \cdot (3,-\frac{25}{2}, -6) \eql 0 $$ So, these two are orthogonal and because two vectors are enough for the grey plane, they form an orthogonal basis.
     

    Orthogonal spaces:

    • Let's go back to the vectors \({\bf y}\) and \({\bf w}\) above, both of which were on the same line:

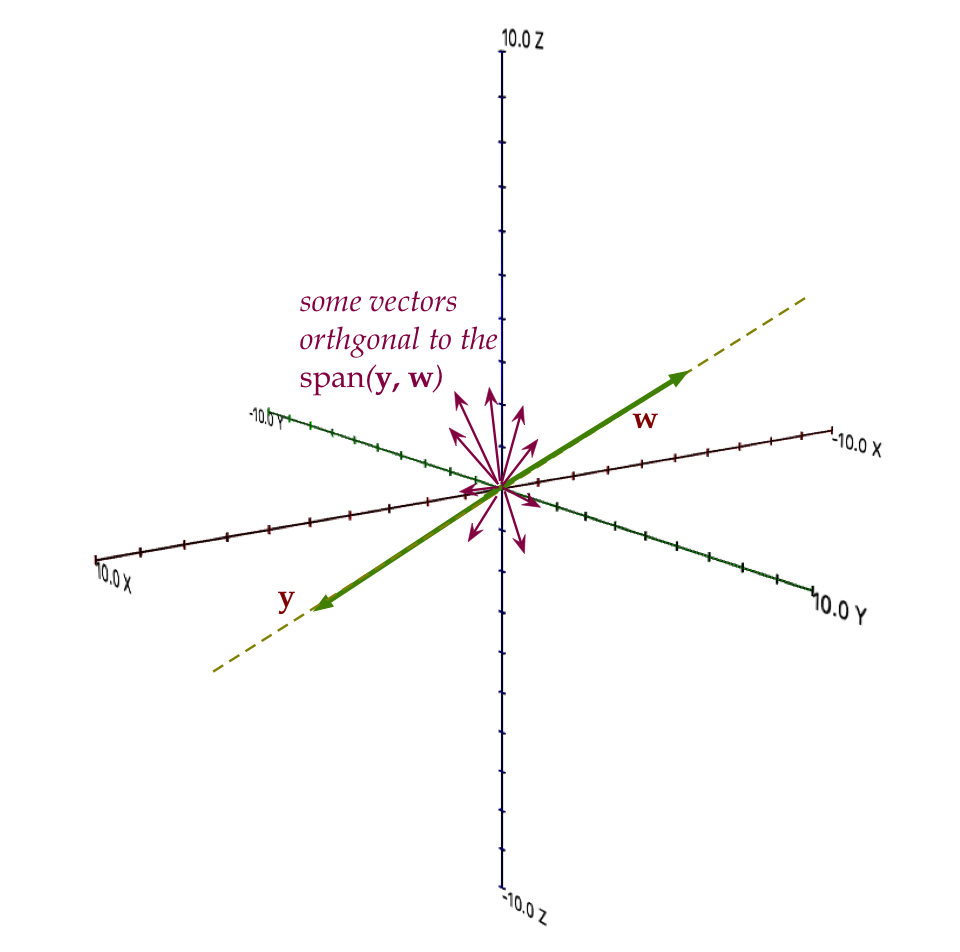
    • Now, \(\mbox{span}({\bf y,w})\) is a subspace, because all linear combinations of any two vectors on this line are on the line.

    • Consider all the vectors orthogonal to \({\bf y}\).
      • These are all going to be on a plane to which the line is perpendicular.
      • Example vectors on this perpendicular plane are shown above.

    • Let \({\bf S}\) be the subspace of vectors on this perpendicular plane (perpendicular to the line).
      • Notice: every vector in \({\bf S}\) is perpendicular to every vector in \(\mbox{span}({\bf y,w})\).
      • Thus, \({\bf S}\) and \(\mbox{span}({\bf y,w})\) are orthogonal subspaces.
      • There's notation for this: $$ {\bf S}^\perp \eql \mbox{span}({\bf y,w}) $$ and $$ {\bf S} \eql \mbox{span}({\bf y,w})^\perp $$

    • Orthogonal subspaces aren't really seen in practice, but they are useful in proofs.
     

    Let's review independence:

    • Vectors \({\bf v}_1, {\bf v}_2, \ldots, {\bf v}_n\) are linearly independent if the only solution to the equation $$ x_1 {\bf v}_1 + x_2 {\bf v}_2 + \ldots + x_n {\bf v}_n \eql {\bf 0} $$ is \(x_1 = x_2 = \ldots = x_n = 0\).
      • Here, the \({\bf v}_i\)'s are vectors (any dimension: 2D, 3D, whatever).
      • Every vector in the collection needs to be non-zero (otherwise, trivially, a zero-vectors coefficient can be anything, and the definition will fail).
      • The \(x_i\)'s are numbers (scalars in the linear combination)
      • Notice the right side: that's the zero vector of the same dimension as any of the \({\bf v}_i\)'s $$ {\bf 0} \eql (0,0,\ldots,0) $$

    • Consider these three vectors: $$\eqb{ {\bf u} & \eql & (4,0,2) \\ {\bf v} & \eql & (0,5,3) \\ {\bf r} & \eql & (-3,-\frac{25}{2},-6) \\ }$$ Are they independent?
      • Observe that $$\eqb{ \frac{3}{4} {\bf u} - \frac{5}{2}{\bf v} - {\bf r} & \eql & \frac{3}{4}(4,0,2) - \frac{5}{2}(0,5,3) - (-3,-\frac{25}{2},-6)\\ & \eql & (0,0,0) }$$
      • So, in setting $$ x_1 {\bf u} + x_2 {\bf u} + x_3 {\bf r} \eql {\bf 0} $$ we know that \((x_1,x_2,x_3) = (\frac{3}{4}, -\frac{5}{2}, -1)\) is one possible solution (there are others).
      • This is a non-zero solution and hence the three are not independent.
      • Which makes sense since all three lie on the plane (from earlier):

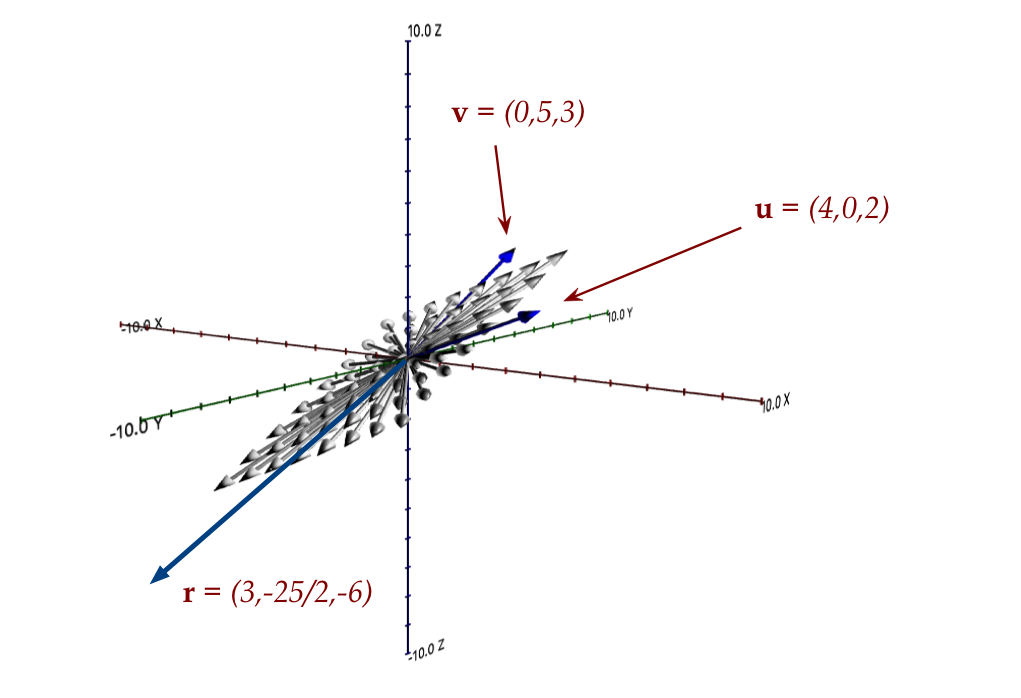
    • How can we check, given a collection of vectors, that they are independent?
      • Recall, we are asking for the solution to $$ x_1 {\bf v}_1 + x_2 {\bf v}_2 + \ldots + x_n {\bf v}_n \eql {\bf 0} $$
      • Place the vectors as columns of a matrix \({\bf A}\): $$ {\bf A} \eql \mat{ & & & \\ \vdots & \vdots & \ldots & \vdots \\ {\bf v}_1 & {\bf v}_2 & \ldots & {\bf v}_n\\ \vdots & \vdots & \ldots & \vdots \\ & & & } $$
      • So, $$ x_1 {\bf v}_1 + x_2 {\bf v}_2 + \ldots + x_n {\bf v}_n \eql {\bf 0} $$ becomes $$ \mat{ & & & \\ \vdots & \vdots & \ldots & \vdots \\ {\bf v}_1 & {\bf v}_2 & \ldots & {\bf v}_n\\ \vdots & \vdots & \ldots & \vdots \\ & & & } \mat{x_1\\ x_2\\ x_3\\ \vdots\\ x_n} \eql \mat{0\\ 0\\ 0\\ \vdots\\ 0} $$
      • Or, more compactly: solve \({\bf Ax} = {\bf 0}\).
      • This is something we know how to do (compute the RREF etc).

    • From Theorem 8.1 we know that:
      • When \(\mbox{RREF}({\bf A}) = {\bf I}\) (i.e., the RREF is full-rank), then \({\bf x}={\bf 0}\) is the only solution to \({\bf Ax} = {\bf 0}\).
      • Thus, the vectors will be independent if the RREF is full-rank (a pivot in every column).
      • This gives us a means to identify whether a collection of vectors is independent: put them in a matrix and check its RREF.
     

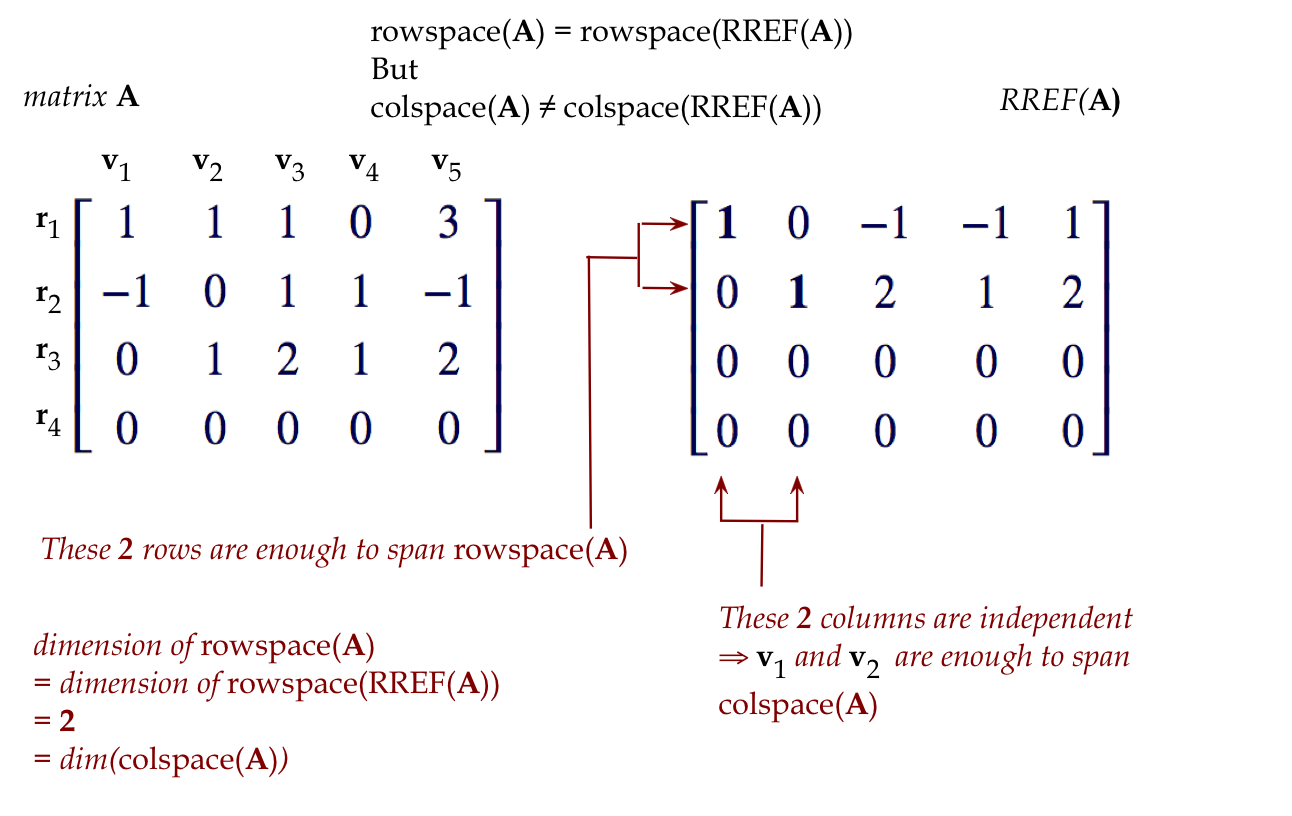
    Lastly, let's review the rowspace and colspace of a matrix:

    • Consider a matrix like $$ {\bf A} \eql \mat{1 & 1 & 1 & 0 & 3\\ -1 & 0 & 1 & 1 & -1\\ 0 & 1 & 2 & 1 & 2\\ 0 & 0 & 0 & 0 & 0} $$

    • Let's treat the rows as vectors and name them: $$\eqb{ {\bf r}_1 & \eql & (1,1,1,0,3)\\ {\bf r}_2 & \eql & (-1,0,1,1,-1)\\ {\bf r}_3 & \eql & (0,1,2,1,2)\\ {\bf r}_4 & \eql & (0,0,0,0,0) }$$

    • Then the span of these vectors is the rowspace of the matrix: $$ \mbox{rowspace}({\bf A}) \eql \mbox{span}({\bf r}_1, {\bf r}_2, {\bf r}_3, {\bf r}_4) $$
      • That is, any linear combination of the four row vectors is in the rowspace.
      • Example: $$\eqb{ 2{\bf r}_1 + 3 {\bf r}_2 + 0 {\bf r}_3 +5 {\bf r}_4 & \eql & 2(1,1,1,0,3) + 3(-1,0,1,1,-1) + 0(0,1,2,1,2) + 5(0,0,0,0,0)\\ & \eql & (-1,2,5,3,3) }$$ So \((-1,2,5,3,3)\) is a vector in the rowspace.

    • Similarly, if we name the 5 columns \({\bf c}_1, {\bf c}_2, {\bf c}_3,{\bf c}_4,{\bf c}_5\) then the colspace is their span: $$ \mbox{colspace}({\bf A}) \eql \mbox{span}({\bf c}_1, {\bf c}_2, {\bf c}_3,{\bf c}_4,{\bf c}_5) $$

    • What's of interest here is:
      1. What is the dimension of the rowspace, that is, how many vectors are needed for a basis of the rowspace?
      2. (same question for colspace)

    • Now the RREF turns out to be: $$ \mat{{\bf 1} & 0 & -1 & -1 & 1\\ 0 & {\bf 1} & 2 & 1 & 2\\ 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0} $$

    • Clearly, the rowspace of the RREF is the span of the first two rows.

    • Now for the key observation: the row operations we performed do not change the rowspace of the matrices along the way from \({\bf A}\) to its RREF.

    • Why?
      • All row operations are linear combinations of rows.
      • To see why, just recall how we wrote them. Example: \({\bf r}_1 \leftarrow {\bf r}_1 - 2{\bf r}_2\).

    • Unfortunately, it is not true that \(\mbox{colspace}({\bf A}) = \mbox{colspace}(RREF({\bf A}))\).

    • What is true is that the size of the basis for \(\mbox{colspace}({\bf A})\) is the same as the number of pivot columns.

    • Because pivots are alone in both their rows and columns, we get the remarkable result that the dimension of the rowspace is the same as the dimension of the colspace.

    • All of this is summarized in a picture we saw before:

     

    r.7    Orthogonality

     

    There are two subtopics of orthogonality that commonly appear in applications:

    1. Orthogonal vectors and matrices.
    2. Projections.
     

    Let's start with orthogonal vectors:

    • Two vectors \({\bf u}\) and \({\bf v}\) are orthogonal if $$ {\bf u} \cdot {\bf v} \eql 0 $$ Note:
      • The right side is the number 0 (since the dot product gives us a number).
      • This is unlike the linear independence definition where the \({\bf 0}\) on the right side is the zero vector.
      • The definition comes from the angle between them, which is a right-angle: $$ \cos(\theta) \eql \frac{ {\bf u} \cdot {\bf v}}{ |{\bf u}||{\bf v}|} $$ Since the lengths aren't zero, if the dot product is zero, that implies a zero cosine, or \(\theta=90^\circ\).

    • This definition extends to a collection of vectors:
      • Consider vectors \({\bf v}_1,{\bf v}_2,{\bf v}_3\).
      • The collection is orthogonal if $$\eqb{ {\bf v}_1 \cdot {\bf v}_2 & \eql & 0\\ {\bf v}_1 \cdot {\bf v}_3 & \eql & 0\\ {\bf v}_2 \cdot {\bf v}_3 & \eql & 0 }$$ Since dot-product is commutative we don't need to specify products like \({\bf v}_2 \cdot {\bf v}_2 = 0\).

    • Example: \({\bf v}_1=(4,4,4), {\bf v}_2=(4,-8,4), {\bf v}_3=(6,0,-6)\) $$\eqb{ {\bf v}_1 \cdot {\bf v}_2 & \eql & (4,4,4) \cdot (4,-8,4) & \eql & 0\\ {\bf v}_1 \cdot {\bf v}_3 & \eql & (4,4,4) \cdot (6,0,-6) & \eql & 0\\ {\bf v}_2 \cdot {\bf v}_3 & \eql & (4,-8,4) \cdot (6,0,-6) & \eql & 0\\ }$$

    • Now consider this equation $$ \alpha_1 {\bf v}_1 + \alpha_2 {\bf v}_2 + \alpha_3 {\bf v}_3 = {\bf 0} $$ Does this imply that all the \(\alpha\)'s are zero, and therefore the \({\bf v}\)'s are independent?
      • Multiply (dot product) both sides by \({\bf v}_1\): $$ {\bf v}_1 \cdot (\alpha_1 {\bf v}_1 + \alpha_2 {\bf v}_2 + \alpha_3 {\bf v}_3) \eql {\bf v}_1 \cdot {\bf 0} $$
      • The right side becomes the number 0.
      • Do the algebra on the left side, passing the dot into the parens: $$ \alpha_1 ({\bf v}_1 \cdot {\bf v}_1) + \alpha_2 ({\bf v}_1 \cdot {\bf v}_2) + \alpha_3 ({\bf v}_1 \cdot {\bf v}_3) \eql 0 $$
      • Because they are orthogonal, only non-zero dot product is the first one, so $$ \alpha_1 ({\bf v}_1 \cdot {\bf v}_1) + 0 + 0 \eql 0 $$
      • Now apply the dot product $$ {\bf v}_1 \cdot {\bf v}_1 \eql |{\bf v}_1| |{\bf v}_1| \cos(0) $$
      • And so, we get $$ \alpha_1 |{\bf v}_1| |{\bf v}_1| \eql 0 $$
      • Which, because \(|{\bf v}_1| \neq 0\), implies that $$ \alpha_1 \eql 0 $$

    • To conclude, an orthogonal collection is linearly independent.
      • This makes sense geometrically too.
      • For example, with the three vectors in the example above:

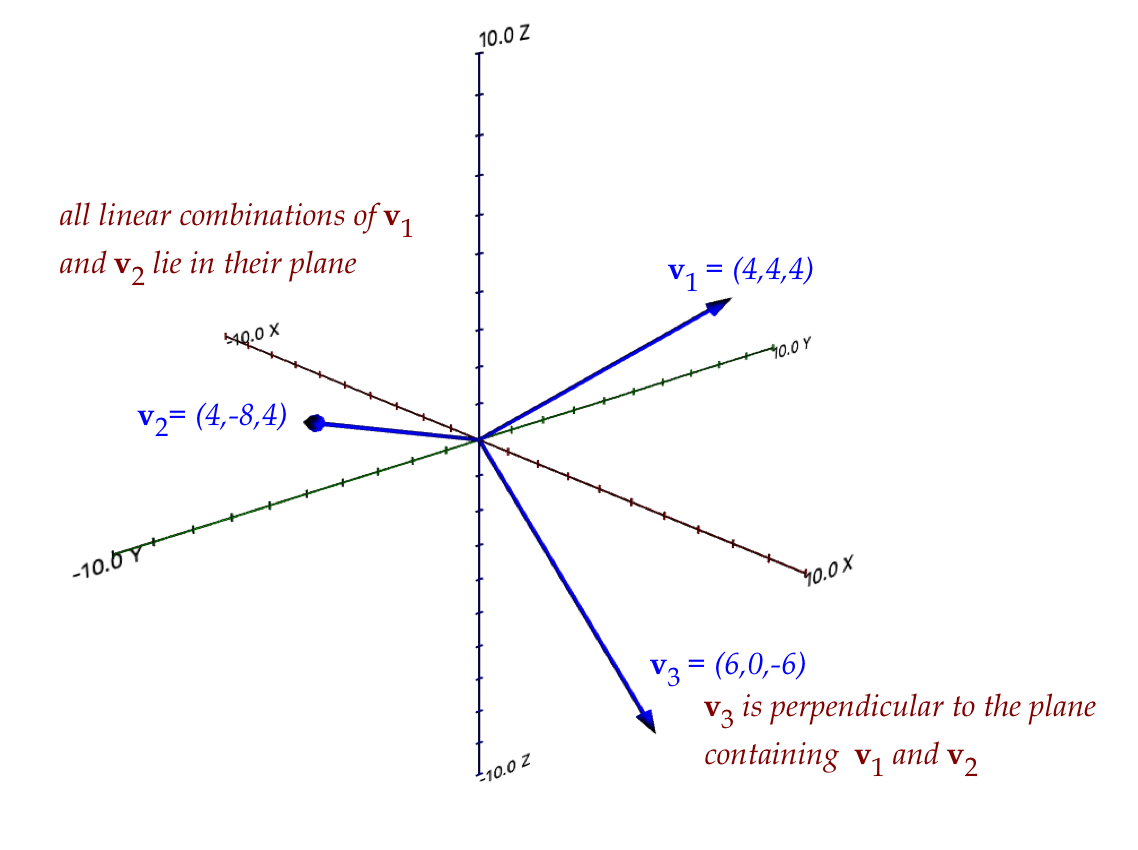
      • \({\bf v}_3\) is not in the plane of \({\bf v}_1\) and \({\bf v}_2\), and so, cannot be expressed as a linear combination of \({\bf v}_1\) and \({\bf v}_2\).
     

    What about complex vectors?

    • The visualization problem with complex vectors (even 2D complex vectors) is that we can't draw them.

    • For example, consider these two 3-component complex vectors: $$\eqb{ {\bf u} & \eql & (1 + 0i, \; -0.5 + 0.866i, \; -0.5 - 0.866i)\\ {\bf v} & \eql & (1 + 0i, \; 1 + 0i, \; 1 + 0i) }$$

    • We can't really visualize because there's no convenient way of drawing a complex vector like this, and so, there's no geometric way to define an angle between them.

    • However, their dot-product is: $$ (1 + 0i)(1 - 0i) + (-0.5+0.866i)(1-0i) + (-0.5 - 0.866i)(1 - 0i) \eql 0 $$ (Recall: we conjugate the elements of the second vector.)

    • Thus, we define orthogonality between two complex vectors to mean: their dot-product is zero.
     

    Orthogonal matrices

    • First, let's sort out orthogonal vs orthonormal.
    • Two vectors \({\bf u}\) and \({\bf v}\) are orthonormal if
      1. They are orthogonal.
      2. They have unit length: \(|{\bf u}| = 1\), \(|{\bf v}| = 1\)

    • There is, unfortunately, a bit of confusing nomenclature regarding orthogonal matrices.

    • An orthogonal matrix is a matrix whose columns are pairwise orthonormal.

    • Note: pairwise means "all possible pairs" like column 2 and column 5.

    • For example, consider $$ {\bf A} \eql \mat{4 & 4 & 6\\ 4 & -8 & 0\\ 4 & 4 & -6} $$ You can check that the columns are pairwise orthogonal but not orthonormal.
      • For example: \(|(4,4,4)| = \sqrt{4^2+4^2+4^2} = 6.92820\).

    • However, this matrix is orthonormal: $$ {\bf Q} \eql \mat{0.577 & 0.408 & 0.707\\ 0.577 & -0.816 & 0.408\\ 0.577 & 0 & -0.707} $$ The columns are pairwise orthogonal and all have unit length.

    • What's nice about an orthonormal matrix is this: $$ {\bf Q}^T {\bf Q} \eql {\bf I} $$

    • With the above example: $$ {\bf Q}^T {\bf Q} \eql \mat{0.577 & 0.577 & 0.577\\ 0.408 & -0.816 & 0\\ 0.707 & 0.408 & -0.707} \mat{0.577 & 0.408 & 0.707\\ 0.577 & -0.816 & 0.408\\ 0.577 & 0 & -0.707} \eql \mat{1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1} $$ To see why:
      • The row i, column j entry of the product is the dot product of row i from \({\bf Q}^T\) and column j from \({\bf Q}\)
      • But row i from \({\bf Q}^T\) is just column i from \({\bf Q}\)
      • When \(i\neq j\) column i and column j from \({\bf Q}\) are orthonormal and so their dot-product is 0.
      • When i=j, it's the dot-product of a column with itself, which is 1.

    • The important implication is that \({\bf Q}^T\) is the inverse of \({\bf Q}\).
     

    r.8    Projections

     

    Let's start with a 2D example:

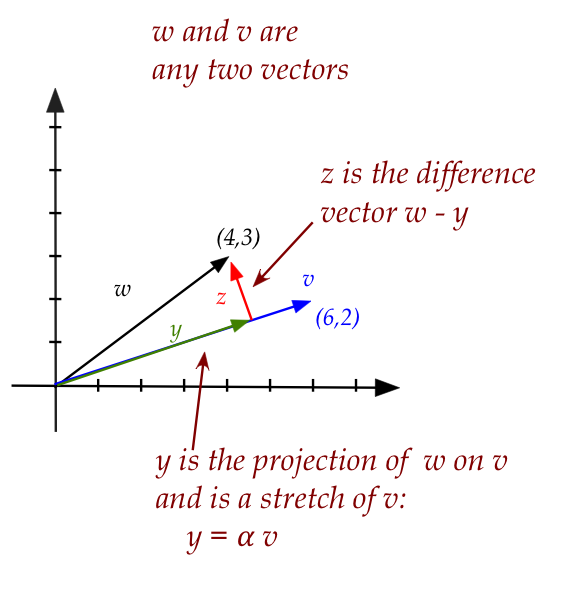
    • Here, \({\bf w}\) and \({\bf v}\) are any two vectors.

    • The projection of \({\bf w}\) on \({\bf v}\) is that vector \({\bf y}\) along \({\bf v}\) which will make the difference perpendicular (dot product zero): $$ ({\bf w} - \alpha{\bf v}) \cdot {\bf v} \eql 0\\ $$ That is, there is some stretch \(\alpha {\bf v}\) of \({\bf v}\) which will make the difference \({\bf z}\) perpendicular to \({\bf v}\).

    • We can solve for the number \(\alpha\): $$ \alpha \eql \frac{{\bf w} \cdot {\bf v}}{{\bf v} \cdot {\bf v}} $$

    • When, for example, $$\eqb{ {\bf w} & \eql & (4,3) \\ {\bf v} & \eql & (6,2) }$$ we get $$ \alpha \eql \frac{(4,3) \cdot (6,2)}{(6,2) \cdot (6,2)} \eql 0.75 $$

    • Although we have drawn the above with 2D vectors, a projection from one vector to another works in any number of dimensions, for example:

     

    Next, let's look at a 3D vector that's projected onto a plane whose basis is orthogonal:

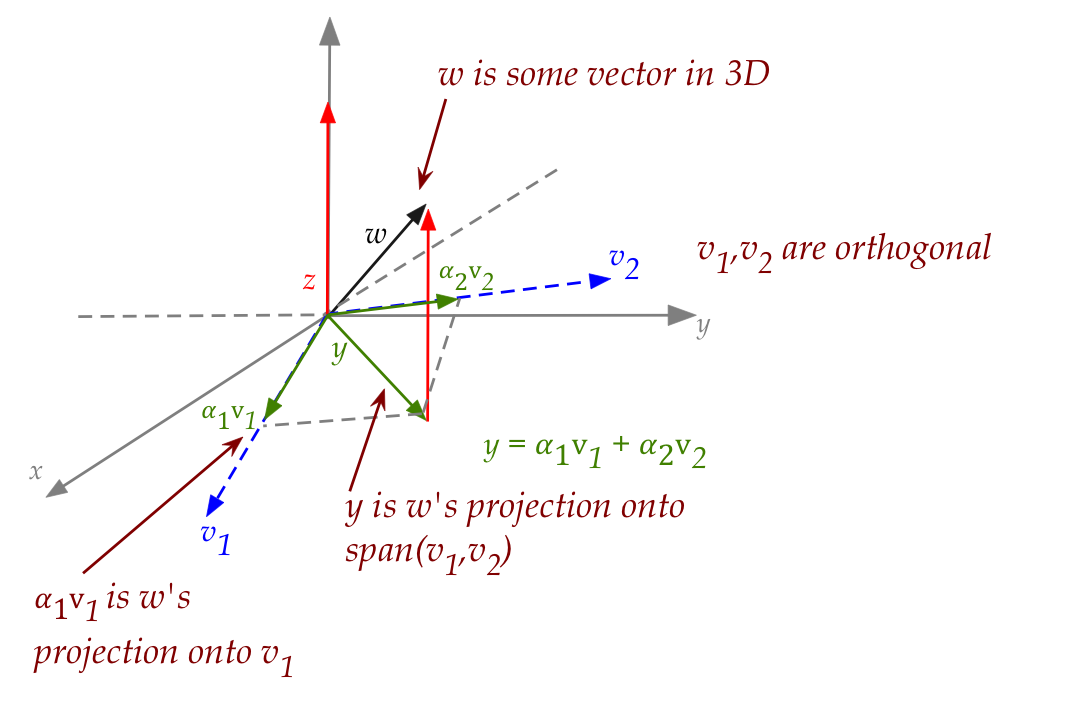
    Let's make sense of this busy picture:

    • Think of \({\bf w}\) as a regular 3D vector sticking out into 3D space.

    • Next, let \({\bf v}_1\) and \({\bf v}_2\) be two orthogonal vectors in the x-y plane.

    • We want to ask: what's the projection of \({\bf w}\) onto each of \({\bf v}_1\) and \({\bf v}_2\) and what do those individual projections have to do with \({\bf y}\), the projection of \({\bf w}\) on the span of the two vectors?

    • The individual projections are: $$\eqb{ \alpha_1 {\bf v}_1 \\ \alpha_2 {\bf v}_2 \\ }$$ where $$\eqb{ \alpha_1 & \eql & \frac{{\bf w} \cdot {\bf v}_1}{{\bf v}_1 \cdot {\bf v}_1}\\ \alpha_2 & \eql & \frac{{\bf w} \cdot {\bf v}_2}{{\bf v}_2 \cdot {\bf v}_2}\\ }$$

    • But the sum of these is exactly \({\bf y}\): $$ {\bf y} \eql \alpha_1{\bf v}_1 + \alpha_2{\bf v}_2 $$

    • Note: you cannot reconstruct the original vector \({\bf w}\) knowing only the individual projections \(\alpha_1{\bf v}_1\) and \(\alpha_2{\bf v}_2\).

    • That's because \({\bf w}\) is not in the same space as \({\bf v}_1\) and \({\bf v}_2\).
     

    So, finally, let's look at the case when \({\bf w}\) is in the span of \({\bf v}_1\) and \({\bf v}_2\).

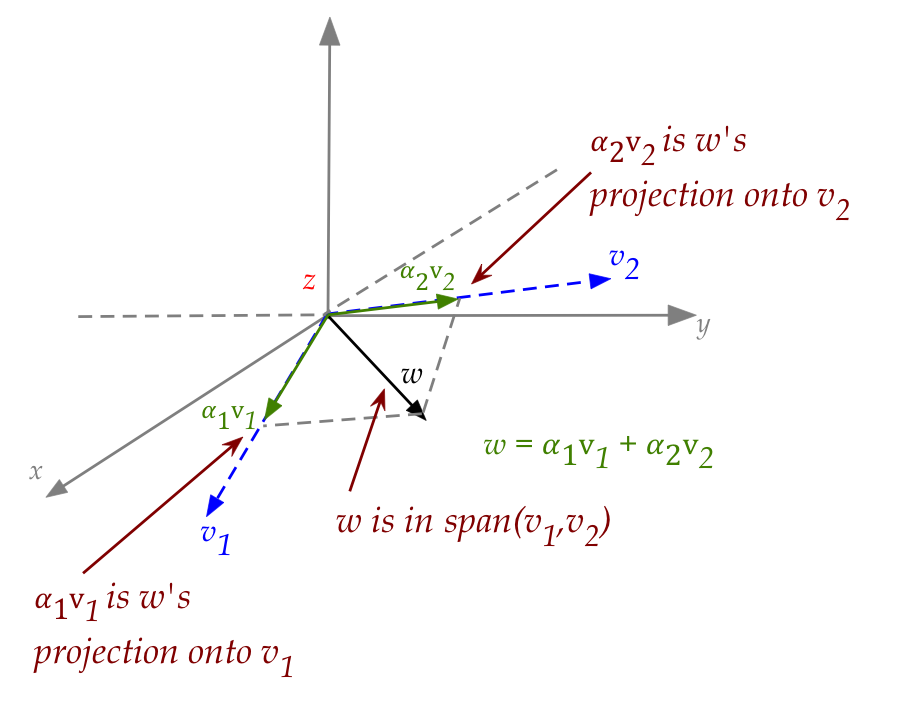
    In this case:

    • The individual projections add up to the original vector \({\bf w}\): $$ {\bf w} \eql \alpha_1{\bf v}_1 + \alpha_2{\bf v}_2 $$

    • Thus, when \({\bf w}\) is in the span of \({\bf v}_1\) and \({\bf v}_2\), we can fully reconstruct \({\bf w}\) knowing only the individual projections on the basis vectors.

    • Note: although we have used a basis for the x-y plane, the above reasoning applies to any subspace and any orthogonal basis for that subspace.

    • Thus, in the general case we'd say that $$ {\bf w} \eql \alpha_1{\bf v}_1 + \alpha_2{\bf v}_2 \; \ldots \; + \alpha_n{\bf v}_n $$ where $$ \alpha_i \eql \frac{{\bf w} \cdot {\bf v}_i}{{\bf v}_i \cdot {\bf v}_i} $$
     

    A further simplification when the basis is orthonormal:

    • When the \({\bf v}_i\)'s are orthonormal, they have unit length and so $$ {\bf v}_i \cdot {\bf v}_i \eql |{\bf v}_i|^2 \eql 1. $$ Which means $$ \alpha_i \eql {\bf w} \cdot {\bf v}_i $$

    • Then $$ {\bf w} \eql ({\bf w} \cdot {\bf v}_1) {\bf v}_1 + \; \ldots \; + ({\bf w} \cdot {\bf v}_n) {\bf v}_n $$ This is worth remembering: many applications use orthonormal bases.
     

    Go to Part III
     

    © 2020, Rahul Simha