Module 8: Graphs, Part II

On-line versus Off-line Problems

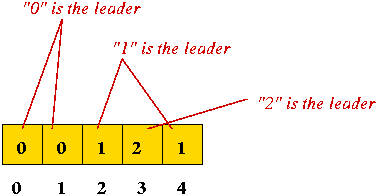
Consider the Equivalence Class Problem:

Input: "relationship pairs", e.g.


    (A, B)
    (D, E)
    (B, A)
    (E, D)
    (A, C)

Desired output: identify equivalence classes (connected components):

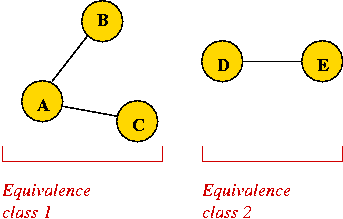
Thus, output for this example:


    class 0: A, B, C
    class 1: D, E

Off-line version:

Entire input is given at once.
Solution:
- Scan input and place edges in undirected graph.
- Run depth-first search to identify components and label each vertex.
- Scan labels and print out classes (components).
Analysis: O(V + E).
(Here, E = number of input pairs.)

On-line version of problem:

First, number of elements (vertices) is given to algorithm.
Then, the algorithm receives one pair (edge) at a time.

Algorithm must output current equivalence classes at each step, e.g.


    Input: (A, B)
    Output:
       class 0: A, B
       class 1: C
       class 2: D
       class 3: E

    Input: (D, E)
    Output:
       class 0: A, B
       class 1: C
       class 2: D, E

    Input: (B, A)
    Output:
       class 0: A, B
       class 1: C
       class 2: D, E

    Input: (E, D)
    Output:
       class 0: A, B
       class 1: C
       class 2: D, E

    Input: (A, C)
    Output:
       class 0: A, B, C
       class 1: D, E

About on-line problems:

Input is usually a "sequence of data values".
(Called request sequence).
Input is revealed one piece at a time.
Algorithm must output current (partial) solution after each input.
Algorithm cannot know future input in the sequence.
Algorithm is allowed to use past input.
Data is allowed to repeat, e.g., "vertices" and "edges" repeat in edge sequence.
Typical analysis:
- Given an input sequence of size m about n items, what is the time taken in terms of m and n?

Using depth-first search for the on-line equivalence class problem:

After reading each "edge", run depth-first search to identify components.

In-Class Exercise 8.1: For n vertices and a sequence of m edges, how long does the above algorithm take to process the whole sequence?

Union-Find Algorithms: Solving the On-line Equivalence Class Problem

Key ideas:

The equivalence class problem can expressed a little differently
=> the Union-Find Problem.

Union-Find:

Given: initial collection of "singleton" sets, e.g.
```
     A, B, C, D, E
     
```

Input: sequence of (possibly interspersed) "union" or "find" operations, e.g.,


    union (A, B)
    find (A)
    find (C)
    union (D, E)
    union (B, A)
    find (D)
    find (E)
    union (E, D)
    union (A, C)
    find (C)
    find (A)

Output: return the current set identifier (equivalence class) after each "find" operation, e.g.,


    union (A, B)
    find (A)
    Output: set 0

    find (C)
    Output: set 1

    union (D, E)
    union (B, A)
    find (D)
    Output: set 2

    find (E)
    Output: set 2

    union (E, D)
    union (A, C)
    find (C)
    Output: set 0

    find (A)
    Output: set 0

In-Class Exercise 8.2: What is the output after each find operation in the following sequence on nodes A through H?


  union (A, B)
  union (A, C)
  find (C)
  find (D)
  union (G, H)
  union (F, G)
  find (H)
  union (C, F)
  find (H)

ADT (Abstract Data Type) for a union-find algorithm:

ADT with object-items:


public interface UnionFindAlgorithm extends Algorithm {

  // Initialize with number of items (e.g., number of vertices) 
  public void initialize (int maxValues);

  // Call this repeatedly to instantiate initial sets. 
  public void makeSingleElementSet (Object value);

  // Union operation. 
  public void union (Object value1, Object value2);

  // Find operation: returns the ID of the set that currently contains "value". 
  public int find (Object value);

}

For integer-items: we would use


public interface UnionFindAlgorithm extends Algorithm {

  // Initialize with number of items (e.g., number of vertices) 
  public void initialize (int maxValues);

  // Call this repeatedly to instantiate initial sets. 
  public void makeSingleElementSet (int value);
  
  // Union operation. 
  public void union (int value1, int value2);

  // Find operation: returns the ID of the set that currently contains "value". 
  public int find (int value);

}

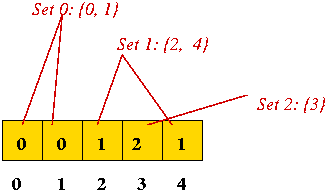
The Quick-Find Algorithm:

Assume: data consists of integers (0, 1, 2, ...)
(Slight modification required for objects).
Key ideas:
- Maintain set ID's in an array:
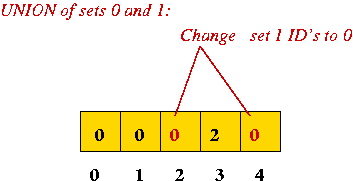
- Every union operation merges two sets
  => they need to have the same ID
  => write first set ID over the set ID's of second set members:
- Find operation: simply return set ID.
Analysis:
- Find operation: O(1)
- Union operation: O(n) (worst-case)
- For m operations on n items: O(mn) worst-case.

Pseudocode:


Algorithm: union (value1, value2)
Input: two values, whose sets are to be combined.

     // Important: Assume initialization is complete, and ID[i] = i initially. 

     // If they are in the same set, nothing to be done. 
1.   if ID[value1] = ID[value2]
2.       return
3.   endif

     // Otherwise, change the ID of every member in the second set to ID[value1] 
4.   id2 = ID[value2]
5.   for i=0 to numValues-1
6.       if ID[i]=id2
7.           ID[i] = ID[value1]
8.       endif
9.   endfor


Algorithm: find (value)
Input: an item whose set ID needs to be returned

     // ID's are always up-to-date, so return the current set ID. 

1.   return ID[value]

Output: ID of current set that "value" belongs to.

In-Class Exercise 8.3: Look closely at the pseudocode in union above. Why doesn't the following work?


     // Otherwise, change the ID of every member in the second set to ID[value1] 
5.   for i=0 to numValues-1
6.       if ID[i]=ID[value2]
7.           ID[i] = ID[value1]
8.       endif
9.   endfor

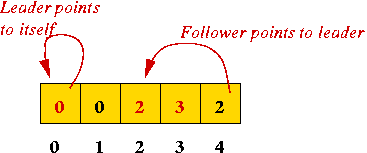
The Leader metaphor:

Suppose each set ID represents a "set leader".
Leaders can be represented using the items themselves.
"Find" operation: return leader's name (ID).
"Union" operation: make two sets have the same leader (same ID).
e.g., merge {0, 1} and {2, 4}.

=> hierarchy: leaders have leaders
Maximum leader: an item who has no leader (points to itself).
Hierarchical view:

The Quick-Union Algorithm:

Idea: try to make "union" faster at the expense of a longer "find".
Union:
- Find the maximum leader of each set.
- Make one leader subservient (point to) to the other.
Find:
- Find the maximum leader, and return ID.

Pseudocode:


Algorithm: union (value1, value2)
Input: two values, whose sets are to be combined.

     // Important: Assume initialization is complete, and ID[i] = i initially. 

     // If they are in the same set, nothing to be done. 
1.   if ID[value1] = ID[value2]
2.       return
3.   endif

     // Identify the two maximum leaders of the sets (which could be the same) 
4.   leader1 = find (value1)
5.   leader2 = find (value2)

     // Either one of the assignments below will do. However, we can 
     // generate as low a set-numbering as possible with this extra 
     // O(1) computation. 
6.   if leader1 < leader2
7.       ID[leader2] = ID[leader1]
8.   else
9.       ID[leader1] = ID[leader2]
10.  endif


Algorithm: find (value)
Input: an item whose set ID needs to be returned

     // Start with the leader of the value (which may point to itself). 
1.   nextLeader = ID[value]

     // Go up the hierarchy to the (unique) maximum leader of this set. 
     // The maximum leader will point to itself. 
2.   while ID[nextLeader] != nextLeader
3.       nextLeader = ID[nextLeader]
4.   endwhile

     // Return the leader itself. 
5.   return nextLeader

Output: ID of current set that "value" belongs to.

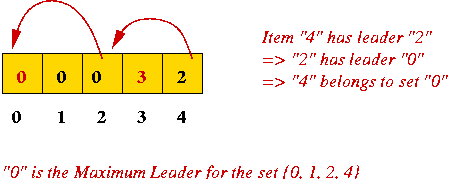
A potential problem with Quick-Union:

Consider the set {0, 1, 2, 3, 4, 5, 6, 7}.

And these operations:


    union (7, 6)
    union (6, 5)
    union (5, 4)
    union (4, 3)
    union (2, 1)
    union (1, 0)
    union (3, 2)

Resulting hierarchy:

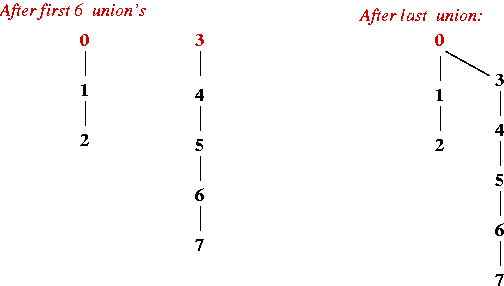
Analysis:
- Worst-case: long tree (O(n) depth).
- Repeat "bad union" operations:
  => O(n²)

Weighted-Union:

Key idea: keep the trees balanced!
Two approaches:
1. Randomize choice of leader.
2. Make leader of smaller tree point to leader of larger tree.
  => requires "size" storage.

Weighted-Union pseudocode:


Algorithm: union (value1, value2)
Input: two values, whose sets are to be combined.

     // Important: Assume initialization is complete, and ID[i] = i  
     // and groupSize[i] = 1 initially. 

     // If they are in the same set, nothing to be done. 
1.   if ID[value1] = ID[value2]
2.       return
3.   endif

     // Identify the two maximum leaders of the sets (which could be the same) 
4.   leader1 = find (value1)
5.   leader2 = find (value2)

     // Make the smaller group point to the larger and update the 
     // group size of the larger group. 
6.   if groupSize[leader1] < groupSize[leader2]
7.       ID[leader1] = ID[leader2]
8.       groupSize[leader2] = groupSize[leader2] + groupSize[leader1]
9.   else
10.      ID[leader2] = ID[leader1]
11.      groupSize[leader1] = groupSize[leader1] + groupSize[leader2]
12.  endif


Algorithm: find (value)
Input: an item whose set ID needs to be returned
 
     // ... same as in Quick-Union algorithm ... (not shown) 

Output: ID of current set that "value" belongs to.

Example:
- Same sequence as before.
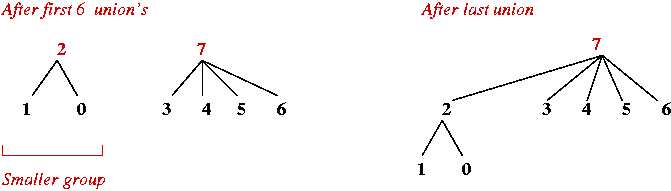
Analysis:
- Worst-case depth of tree: O(log(n)) (tree is approximately balanced).
  (To see why, follow pointers down to smaller sets - reduces size by at least half each time).
- Sequence of m operations: O(m + n log(n)).

A small improvement to "find": (path compression)

Each time "find" is invoked on a value, adjust its leader to point to "leader's leader".
=> halve the path to root with each find operation
=> cuts down depth by half.
Each "halving" action costs O(1).
=> over time, it reduces depth.
Complicated analysis shows: O(m A(m,n)) time where A(m,n) is inverse-Ackerman's function
=> a really slow-growing function.

In-Class Exercise 8.4: Solve the Calling Circle Problem using any of the union-find methods above. Start by writing out pseudocode on paper.

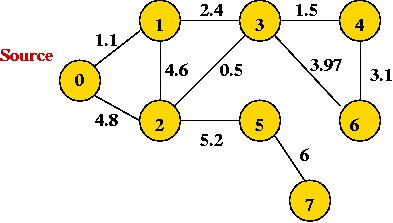
Weighted Graphs

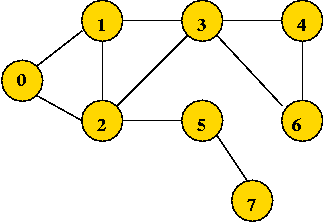
Weighted graphs:

Thus far, we have only considered un-weighted graphs, e.g.,

In a weighted graph, (usually) the edges have weights:

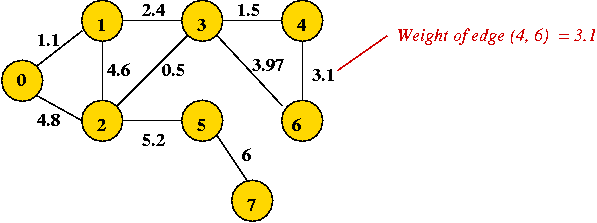
In applications, edge weights usually reflect something like:

The actual distance (geometric).
The cost (installation or rental cost).
Reliability, transmission speed, etc.

Directed graphs:

Each edge has direction.
Even if two vertices have two opposing edges, edge weights can differ (depending on application).
Generally, the algorithms for undirected (weighted) graphs that we will encounter will port over (with minor changes) to directed graphs.

Where are weights stored?

In adjacency-matrix representation, adjMatrix[i][j] = weight of edge (i,j)
In adjacency-list representation, store weight in linked list nodes.

Two important problems with weighted graphs:

The Minimum Spanning Tree (MST) Problem:
- Input: a weighted, connected graph.
- Objective: find a sub-graph such that:
  - The sub-graph is a connected tree.
  - The tree contains all graph vertices.
    => it's a spanning tree.
  - The tree weight is defined as the sum of edge-weights in the tree.
  - The tree weight is the least among such spanning trees.
The Shortest Path Problem:
- Input: a weighted, connected graph.
- Objective: find a path between every pair of vertices such that:
  - The path-weight is defined as the weight of edges in the path.
  - The path-weight for a particular pair is the least among all such paths (for the pair).

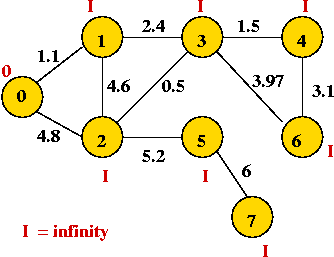
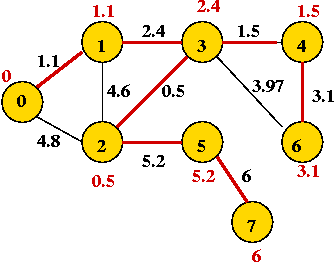
In-Class Exercise 8.4: "Eyeball" the weighted graph below and find the minimum spanning tree, and the shortest path from vertex 0 to vertex 6.

Minimum Spanning Trees: Two Key Observations

The Cut-Edge Observation:

Consider a partition of the vertices into two sets.

Suppose we re-draw the graph to highlight edges going from one set to the other: (without changing the graph itself)

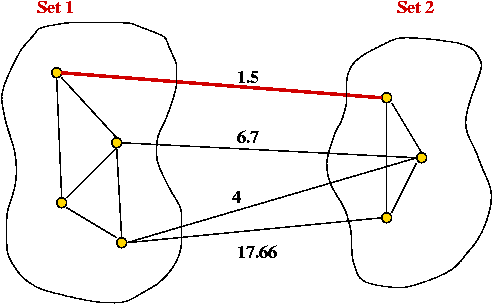
Cut-edge: an edge between the two sets.

Consider the minimum-weight edge between the sets.
(Assume the edge is unique, for now).

The minimum-weight edge must be in the minimum spanning tree.

In-Class Exercise 8.6: Why?

Prim's algorithm (a preview):

Start with Set1 = {vertex 0}, Set2 = {all others}.
At each step, find an edge (cut-edge) of minimum-weight between the two sets.
Add this edge to MST and move endpoint from Set2 into Set1.
Repeat until Set1 = {all vertices}.

The Cycle Property:

First, note: adding an edge whose end-points are in the MST will always cause a cycle.
Consider adding an edge that causes a cycle in current MST.
Suppose the edge has weight larger than all edges in cycle
=> no need to consider adding edge to MST.
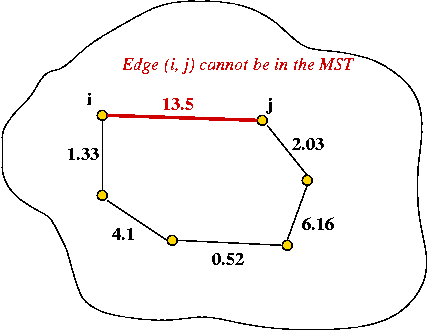
Therefore, if edges are added in order of (increasing) weight
=> no need to consider edges that cause a cycle.

Kruskal's algorithm (a preview):

Sort edges in order of increasing weight.
Process edges in sort-order.
For each edge, add it to the MST if it does not cause a cycle.

Kruskal's Algorithm

Key ideas:

Sort edges by (increasing) weight.

Initially, each vertex is a solitary sub-graph (MST-component).

Start with small MST-component's and grow them into one large MST.

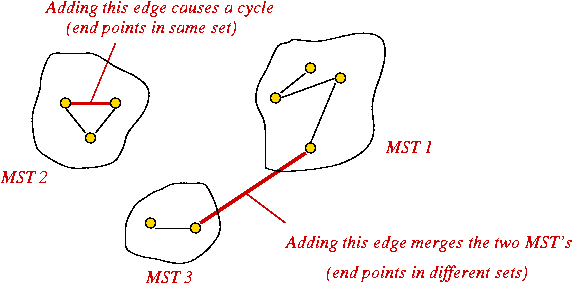
Need to track: which vertex is in which component (i.e., set).

Example:

Initially:

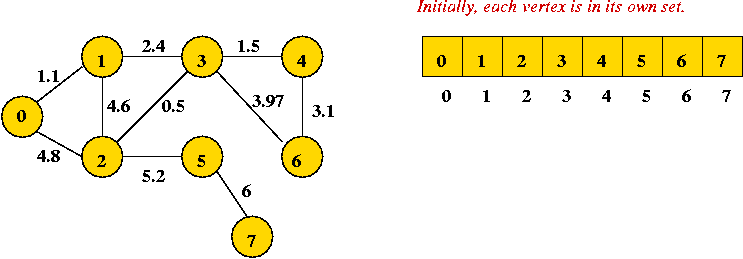
Sort order of edges:


(2, 3),  (0, 1),  (3, 4),  (1, 3),  (4, 6),  (3, 6),  (1, 2),  (0, 2),  (2, 5),  (5, 7)

First edge to add joins "2" and "3" (no cycle):
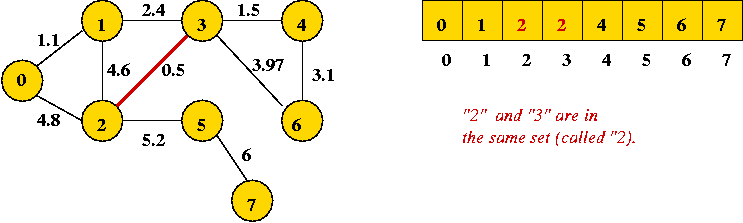
Next edge in sort order: (0, 1):
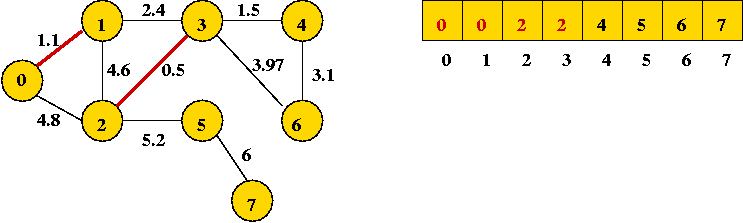
Next edge in sort order: (3, 4):
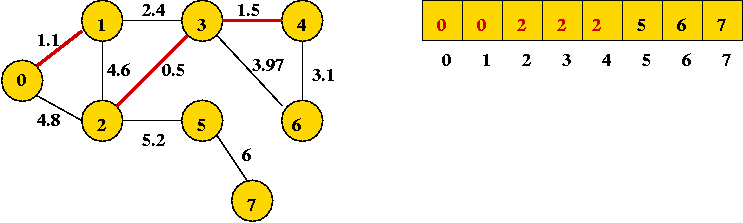
Next edge in sort order: (1, 3): merges two sets (union)
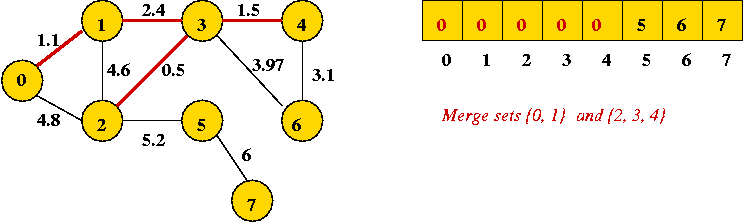
Next edge in sort order: (4, 6):
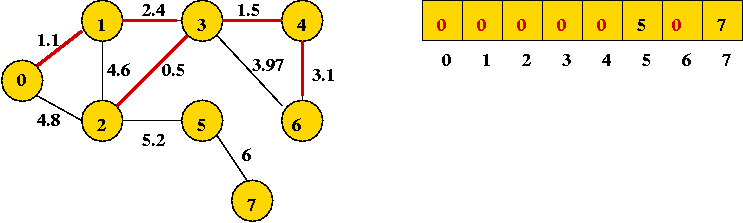
Next edge in sort order: (3, 6): cannot be added
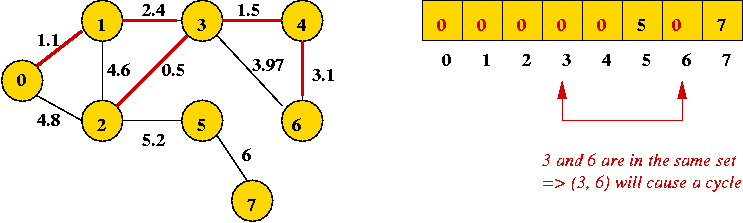
Next two edges also cannot be added: (0, 2) and (1, 2).
Finally, add (2, 5) and (5, 7):

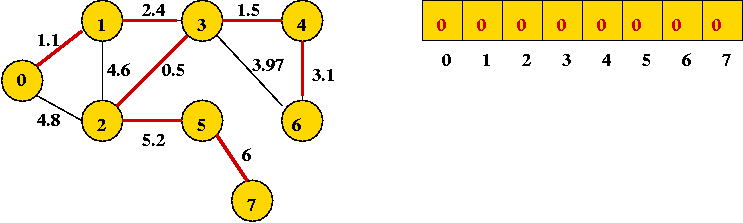
Implementation:

High-level pseudocode:


Algorithm: Kruskal-MST (G)
Input: Graph G=(V,E) with edge-weights.

1.   Initialize MST to be empty;
2.   Place each vertex in its own set;
3.   Sort edges of G in increasing-order;
4.   for each edge e = (u,v) in order
5.       if u and v are not in the same set
6.           Add e to MST;
7.           Compute the union of the two sets;
8.       endif
9.   endfor
10.  return MST

Output: A minimum spanning tree for the graph G.

Now, let's use a union-find algorithm and explain in more detail:


Algorithm: Kruskal-MST (adjMatrix)
Input: Adjacency matrix: adjMatrix[i][j] = weight of edge (i,j) (if nonzero)

1.   Initialize MST to be empty;

     // Initialize union-find algorithm and 
     // place each vertex in its own set. 
2.   for i=0 to numVertices-1
3.       makeSingleElementSet (i)
4.   endfor

5.   sortedEdgeList = sort edges in increasing-order;

6.   Initialize treeMatrix to store MST;

     // Process edges in order. 
7.   while sortedEdgeList.notEmpty()
8.       edge (i,j) = extract edge from sortedEdgeList.
         // If edge does not cause a cycle, add it. 
9.       if find(i) != find(j)
10.          union (i, j)
11.          treeMatrix[i][j] = treeMatrix[j][i] = adjMatrix[i][j]
12.      endif
13.  endwhile

14.  return treeMatrix

Output: adjacency matrix represention of tree.

Sample Java code: (source file)


  // Adjacency matrix version. Return value is tree in matrix form. 
  // Assumption: graph is undirected. 

  public double[][] minimumSpanningTree (double[][] adjMatrix)
  {
    // Union-find: UnionFindInt is an implementation of union-find 
    // for integer values. 
    UnionFindInt unionFind = new UnionFindInt ();
    unionFind.initialize (numVertices);

    // Build the singleton sets. 
    for (int i=0; i < numVertices; i++) 
      unionFind.makeSingleElementSet (i);
    

    // Extract edges from matrix into a form that we can sort. We will 
    // use Java's TreeSet to maintain edges in sort order: TreeSet 
    // guarantees that iteration will occur in sorted order.  
    // Note: we are passing our own Comparator to enable weight-comparisons. 

    TreeSet sortedEdgeSet = new java.util.TreeSet (new EdgeComparator());

    // Enumerate all edges by scanning matrix. 
    for (int i=0; i < numVertices-1; i++) {
      // We don't need both directions since this is undirected. 
      for (int j=i+1; j < numVertices; j++) {
        // Extract edge i, j. 
        if (adjMatrix[i][j] > 0) {

          // GraphEdge stores the endpoints and weight of an edge. 
          GraphEdge edge = new GraphEdge (i, j, adjMatrix[i][j]);
          // Put the edge in our TreeSet. 
          sortedEdgeSet.add (edge);

        }
      }
    } // endfor 


    // Get a matrix ready to hold the MST. 
    treeMatrix = new double [numVertices][];
    for (int i=0; i < numVertices; i++) {
      treeMatrix[i] = new double [numVertices];
      // Already initialized to zero. 
    }

    // Now go through edges one by one in sort order. 
    Iterator iterator = sortedEdgeSet.iterator();

    while (iterator.hasNext()) {

      // Extract next edge. 
      GraphEdge edge = (GraphEdge) iterator.next();

      // We'll use i and j for readability: remove this 
      // for efficiency. 
      int i = edge.startVertex;
      int j = edge.endVertex;

      // See if (i,j) can be added. 
      if ( unionFind.find(i) != unionFind.find(j) ) {

        // Put the two sets together. 
        unionFind.union (i, j);

        // Add to tree (undirected). 
        treeMatrix[i][j] = treeMatrix[j][i] = adjMatrix[i][j];

      }

    } //endwhile 

    return treeMatrix;
  }

Analysis: (adjacency matrix)

Placing edges in list: requires scan of adjacency matrix
=> O(V²).
Sorting edges: O(E log(E)).
One union-find operation for each edge: O(E + V log(V)).
Total: O(V²) + O(E log(E)) + O(E + V log(V))
=> O(V²), for sparse graphs
=> O(V²)log V, for dense graphs

Analysis: (adjacency list)

To place edges in list: simply scan each vertex list once.
=> O(E) time.
Total: O(E)+ O(E log(E)) + O(E + V log(V))
=> O(E log(E))
=> O(E log(V))

Prim's Algorithm

Key ideas:

Start with vertex 0 and set current MST to vertex 0.

At each step, find lowest-weight edge from an MST vertex to a non-MST vertex and add it to MST.

To record the weight of each edge, we will associate edge weight with the vertex that's outside the MST.

We will associate a "priority" with each vertex:
=> intuitively, "priority of vertex v" = "currently known cost of adding v to MST"

Example:

Initially, place vertex 0 in the MST and set the "priority" of each vertex to infinity.
Explore edges from current MST: (0, 1) and (0, 2).
Pick lowest-weight edge (0, 1) to add
=> same as selecting lowest-priority vertex (vertex 1)
Explore edges from newly-added vertex: (1,3), (1,2)

That's why we associate edge-weights with vertices
=> only the edges from the new vertex add new information at each step.
Pick vertex with lowest priority (vertex 3) and explore its edges:
Continuing, we add vertices 2, 4, 6, 5 and 7:

Implementation:

High-level pseudocode:


Algorithm: Prim-MST (G)
Input: Graph G=(V,E) with edge-weights.

1.   Initialize MST to vertex 0.
2.   priority[0] = 0
3.   For all other vertices, set priority[i] = infinity
4.   Initialize prioritySet to all vertices;
5.   while prioritySet.notEmpty()
6.       v = remove minimal-priority vertex from prioritySet;
7.       for each neighbor u of v
             // Explore the edge. 
9.           w = weight of edge (v, u)
8.           if w < priority[u]
9.               priority[u] = w
10.          endif
11.      endfor
12.  endwhile

Output: A minimum spanning tree of the graph G.

More detailed pseudocode: (adjacency matrix)


Algorithm: Prim-MST (adjMatrix)
Input: Adjacency matrix: adjMatrix[i][j] = weight of edge (i,j) (if nonzero)

     // inMST[i] = true once vertex i is in the MST. 
1.   Initialize inMST[i] = false for all i;
2.   Initialize priority[i] = infinity for all i;
3.   priority[0] = 0
4.   numVerticesAdded = 0

     // Process vertices one by one. Note: priorities change as we proceed. 
5.   while numVerticesAdded < numVertices
       // Extract best vertex. 
6.       v = vertex with lowest priority that is not in MST;
         // Place in MST. 
7.       inMST[v] = true
8.       numVerticesAdded = numVerticesAdded + 1
         // Explore edges going out from v. 
9.       for i=0 to numVertices-1
             // If there's an edge and it's not a self-loop. 
10.          if i != v and adjMatrix[v][i] > 0
11.              if priority[i] > adjMatrix[v][i]
                     // New priority. 
12.                  priority[i] = adjMatrix[v][i]
13.                  predecessor[i] = v
14.              endif
15.          endif
16.      endfor
17.  endwhile

18.  treeMatrix = adjacency matrix representation of tree using predecessor array;
19.  return treeMatrix

Output: Adjacency matrix representation of MST

Sample Java code: (source file)


  public double[][] minimumSpanningTree (double[][] adjMatrix)
  {

    // Maintain two sets: one set contains vertices in the current MST. 
    // The other set contains those outside. Prim's algorithm always 
    // adds an edge (the best one) between the two sets. Here,  
    // inSet[i]=true if vertex is in the MST. 

    boolean[] inSet = new boolean [numVertices];

    // vertexKey[i] = priority of vertex i. 
    double[] vertexKeys = new double [numVertices];
    for (int i=0; i < numVertices; i++)
      vertexKeys[i] = Double.MAX_VALUE;   // Infinity. 

    // Set the priority of vertex 0 to 0. 
    vertexKeys[0] = 0;

    // We know we're done when we've added all the vertices.  
    int numVerticesAdded = 1;
    

    // Process vertices one by one. 

    while (numVerticesAdded < numVertices) {

      // Find the best vertex not in the inSet using simple 
      // unsorted array of vertex keys. 
      double min = Double.MAX_VALUE;
      int v = -1;
      for (int i=0; i < numVertices; i++) {
        if ( (! inSet[i]) && (vertexKeys[i] < min) ) {
          min = vertexKeys[i];
          v = i;
        }
      }

      // Put v in the MST. 
      inSet[v] = true;

      numVerticesAdded ++;
      

      // Now scan neighbors in adjMatrix and adjust priorities if needed. 

      for (int i=0; i < numVertices; i++) {

        // Look at row adjMatrix[v][i]. 
        if ( (v != i) && (adjMatrix[v][i] > 0) ) {

          // We have found a neighbor: explore the edge (v,i). 
          double w = adjMatrix[v][i];

          // If the current priority is higher, lower it via edge (v,i). 
          if (vertexKeys[i] > w) {

            // decreaseKey operation. 
            vertexKeys[i] = w;

            // Record predecessor and weight for building MST later. 
            predecessor[i] = v;
            predecessorEdgeWeight[i] = w;

          }

        }

      } //endfor 
      
    } // endwhile 
    

    // Create space for tree. 
    treeMatrix = new double [numVertices][];
    for (int i=0; i < numVertices; i++) {
      treeMatrix[i] = new double [numVertices];
      // Already initialized to zero. 
    }
    
    treeWeight = 0;


    // Now build tree using pred edges. Note: we start from "1" 
    // since "0" is its own predecessor (the root of the tree). 

    for (int i=1; i < numVertices; i++) {

      // (i, pred[i]) has to be an edge. 
      int j = predecessor[i];
      treeMatrix[i][j] = treeMatrix[j][i] = predecessorEdgeWeight[i];
      treeWeight += predecessorEdgeWeight[i];

    }

    return treeMatrix;
  }

Analysis:

Initializations: all are O(V).
There are V iterations of the while-loop.
Finding the lowest-priority: O(V) (scan of priority array).
Scan of neighbors: O(V)
Total work in while-loop: O(V²).
Total time: O(V²).

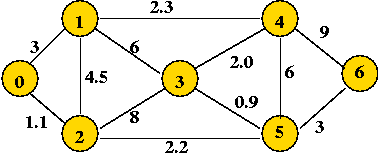
In-Class Exercise 8.7: Use Prim's algorithm, showing all the steps (especially node labels) to find the MST of this graph:

A Priority Queue with the DecreaseKey Operation

What is a priority queue?

Keys or key-value pairs are stored in a data structure.

The operations usually supported are:

Insert: insert a new key-value pair.
Delete: delete a key-value pair.
Search: given a key, find the corresponding value.
Find minimum, maximum among the keys.

Simple implementation with linked-lists:

Keep keys sorted in list.
All operations are straightforward to implement.

A priority queue with the decreaseKey operation:

For convenience, we will combine minimum and remove (delete) into a single operation: extractMin
We would like to change a key while it's in the data structure
=> location in data structure also needs to be changed.
Sorted linked list:
- Potentially O(n) time for decreaseKey
- O(1) time for extractMin
Unsorted array:
- Potentially O(n) time for extractMin
- O(1) time for decreaseKey
Can we do better?
- O(log(n)) time for extractMin
- O(log(n)) time for decreaseKey

Implementing a priority queue with a binary heap:

Recall extractMin operation (Module 2):
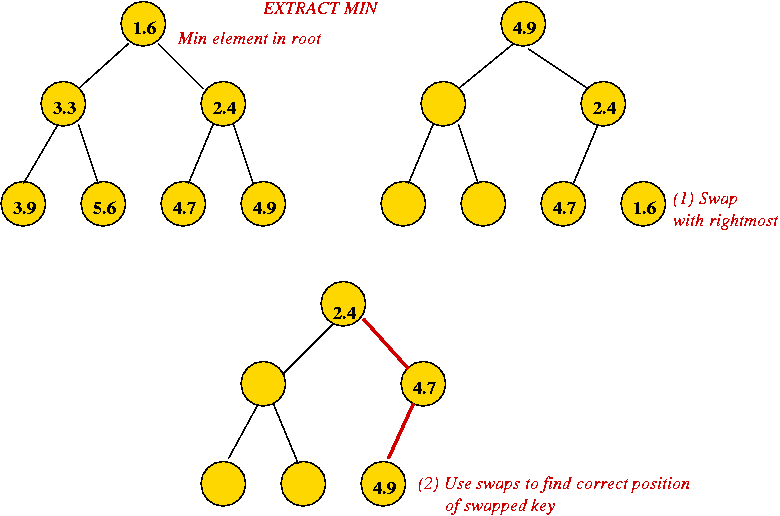
- Height of heap is O(log(n)) always.
- Each extractMin results in changes along one tree path.
  => O(log(n)) worst-case.
Implementing decreaseKey:
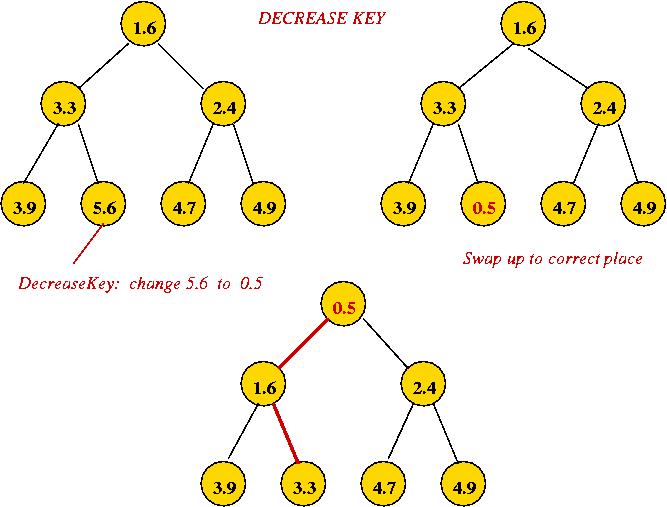
- Simply decrease the value and swap it up towards root to correct location.
  => O(log(n)) worst-case.

Pseudocode:


Algorithm: decreaseKey (heapIndex, newKey)
Input: index in heap-array where key is located, new key value

    // Assume: key-value pairs are stored in an array called data[]. 

    // Change to new key. 
1.  data[heapIndex] = newKey

    // Check up the heap (since it's a decrease operation). 
2.  while heapIndex > 0 
        // Identify parent. 
3.      parentIndex = parent (heapIndex)
4.      if data[parentIndex] > data[heapIndex]
            // If parent is larger, swap up. 
5.          swap (parentIndex, heapIndex)
6.          heapIndex = parentIndex
7.      else
            // Otherwise we've found the right position, so stop. 
8.          heapIndex = -1
9.      endif
10. endwhile

Note: see Module 2 for remaining heap-operations.

Prim's Algorithm with a Priority Queue

Using a priority queue with Prim's algorithm:

We have already been predisposed by using the term "vertex priority".
Use a priority-queue instead of the array priority[i].

However, there are some important implementation details.

First, let's consider the high-level view:

Pseudocode:


Algorithm: Prim-MST (adjMatrix)
Input: Adjacency matrix: adjMatrix[i][j] = weight of edge (i,j) (if nonzero)

     // Initialize vertex priorities and place in priority queue. 
1.   priority[i] = infinity
2.   priorityQueue = all vertices (and their priorities) 
     // Set the priority of vertex 0 to 0. 
3.   decreaseKey (0, 0)

     // Process vertices one by one. 
4.   while priorityQueue.notEmpty()
         // Extract best vertex. 
5.       v = priorityQueue.extractMin()
         // Explore edges going out from v. 
6.       for i=0 to numVertices-1
                 // If there's an edge and it's not a self-loop. 
7.               if i != v and adjMatrix[v][i] > 0
8.                   if priority[i] > adjMatrix[v][i]
                         // Set new priority of neighboring vertex i to edge weight. 
9.                       priorityQueue.decreaseKey (i, adjMatrix[v][i])
10.                      predecessor[i] = v
11.                  endif
12.              endif
13.      endfor
14.  endwhile

15.  treeMatrix = adjacency matrix representation of tree using predecessor array;
16.  return treeMatrix

Output: Adjacency matrix representation of MST

Analysis: adjacency matrix
- Initializations: all are O(V).
- There are V iterations of the while-loop.
- Finding the lowest-priority: O(log(V)) (extract-min).
- Scan of neighbors: O(V)
- Total work in while-loop: O(V²log(V))
  => Not as efficient as simple matrix version!

Analysis: adjacency list

In an adjacency list, we would instead use


Algorithm: Prim-MST (adjList)
Input: Adjacency list: adjList[i] has list of edges for vertex i

     // ... same as in adjacency matrix case ... (not shown) 

4.   while priorityQueue.notEmpty()
         // Extract best vertex. 
5.       v = priorityQueue.extractMin()
         // Explore edges going out from v. 
6.       for each edge e=(v, u) in adjList[v]
7.           w = weight of edge e;
             // If there's an edge and it's not a self-loop. 
8.           if priority[u] > w
                 // New priority. 
9.               priorityQueue.decreaseKey (u, w)
10.              predecessor[u] = v
11.          endif
12.      endfor
13.  endwhile

     // ... build tree in adjacency list form ... (not shown) 

Output: Adjacency list representation of MST

Each edge is processed once.
=> O(E)
=> O(E) decreaseKey operations (worst-case)
=> O(E log(V)) time in decreaseKey operations.
Loop is executed O(V) times
=> O(V) extractMin operations
=> O(V log(V)) cost.
Total time: O(E log(V)) + O(V log(V)) = O(E log(V)).
=> More efficient than matrix-version for sparse graphs.
Note: we have counted costs separately for decrease-Key and extractMin operations, even though they are part of the same code.

Sample Java code: (source file)


  public double[][] minimumSpanningTree (double[][] adjMatrix)
  {

    // Create heap. Note: BinaryHeap implements the PriorityQueueAlgorithm 
    // interface (that has insert, extractMin and decreaseKey operations. 

    PriorityQueueAlgorithm priorityQueue = new BinaryHeap (numVertices);
    priorityQueue.initialize (numVertices);
    

    // Since we are given an adjacency matrix, we need to build vertices 
    // to use in the priority queue. GraphVertex is a class that holds 
    // the vertex id and also can hold an edge-list (Therefore, it's 
    // used for the adjacency-list representation. 
    // NOTE: most importantly, GraphVertex implements the PriorityQueueNode 
    // interface that allows the priority queue to store indices inside the node. 

    GraphVertex[] vertices = new GraphVertex [numVertices];

    // Place vertices in priority queue. 
    for (int i=0; i < numVertices; i++) {
      vertices[i] = new GraphVertex (i);

      if (i != 0) {
        // All vertices except 0 have "infinity" as initial priority. 
        vertices[i].setKey (Double.MAX_VALUE);
        predecessor[i] = -1;
      }
      else {
        // Vertex 0 has 0 as priority. 
        vertices[i].setKey (0);
        predecessor[i] = i;
      }

      priorityQueue.insert (vertices[i]);
    }

    // Now process vertices one by one in order of priority (which changes 
    // during the course of the iteration. 

    while (! priorityQueue.isEmpty() ) {

      // Extract vertex with smallest priority value. 
      GraphVertex vertex = (GraphVertex) priorityQueue.extractMin ();

      // For readability we'll use these shortcuts. 
      int v = vertex.vertexID;
      double v_key = vertex.getKey();

      // Scan neighbors in adjMatrix. 
      for (int i=0; i < numVertices; i++) {

        // Look at row adjMatrix[v][i]. 
        if ( (v != i) && (adjMatrix[v][i] > 0) ) {

          // We have found a neighbor: explore the edge (v,i). 
          double w = adjMatrix[v][i];

          // If the current priority is higher, lower it via edge (v,i). 
          if (vertices[i].getKey() > w) {

            // decreaseKey operation. 
            priorityQueue.decreaseKey (vertices[i], w);

            // Record predecessor and weight for building MST later. 
            predecessor[i] = v;
            predecessorEdgeWeight[i] = w;

          }

        }

      } // endfor 
      
    } // endwhile 
    

    // Create space for tree. 
    treeMatrix = new double [numVertices][];
    for (int i=0; i < numVertices; i++) {
      treeMatrix[i] = new double [numVertices];
      // Already initialized to zero. 
    }
    
    treeWeight = 0;


    // Now build tree using pred edges. Note: we start from "1" 
    // since "0" is its own predecessor (the root of the tree). 

    for (int i=1; i < numVertices; i++) {
      // (i, pred[i]) has to be an edge. 
      int j = predecessor[i];
      treeMatrix[i][j] = treeMatrix[j][i] = predecessorEdgeWeight[i];
      treeWeight += predecessorEdgeWeight[i];
    }

    return treeMatrix;

  }

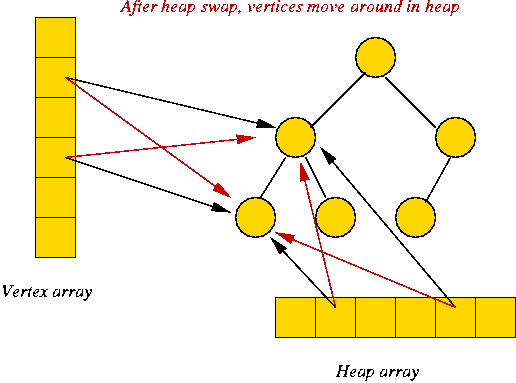
Important implementation detail:

Note: decreaseKey causes changes inside the priority queue data structure.
Changes are to heap indices (since heap is implemented in an array).
If the location of a vertex changes in the heap, how does the algorithm know new location?
(Because the algorithm will need to perform further decreaseKey operations).
Solution: use close relationship between algorithm and data structure.
- In an adjacency-list, adjList[i] is usually an instance of some class like GraphVertex.
- Heap will store heap-indices inside GraphVertex instance itself
  => GraphVertex needs to keep variable for heap index.
- Both algorithm and heap use direct (pointer) reference to each vertex.

Dijkstra's Algorithm for Single-Source Shortest Paths

Single-source?

Typically, we are interested in the shortest path from vertex i to vertex j for every pair i, j.

In the single-source version: we want the shortest path from a given vertex s to every other vertex.

Why single-source?
Because of the shortest path containment property:

Suppose the shortest path from i to j goes through k.
Then, the part of the path up to k is a shortest path to k.
If not, we would be able to create a shorter path to j.

An implication of the containment property:

If all edge weights are unique, the group of paths from a source form a tree.
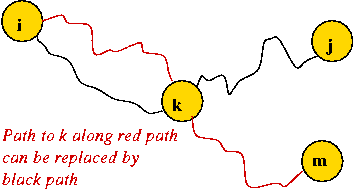
If edge weights are not unique, there exists a tree with equivalent paths (to the group of paths).

Thus, given a source, we can find a shortest-path tree rooted at the source.

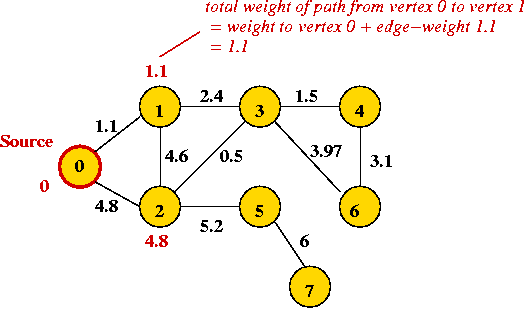
Key ideas in algorithm:

Start at source vertex and grow tree in steps.
At each step identify edges going out from tree to non-tree vertices.
Pick "best" such vertex and add it to tree (along with connecting edge).
Consider edges leading out:

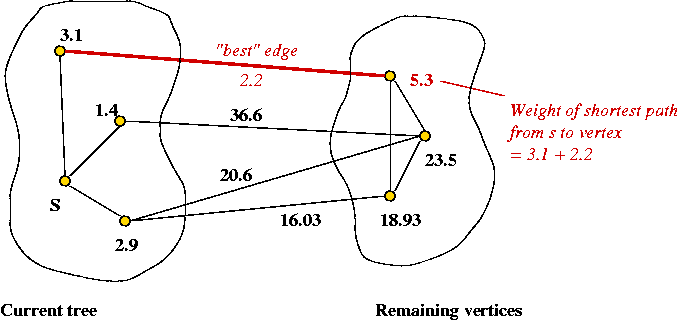
Find the edge leading out that has the least total weight (from source s).
Why does this work?
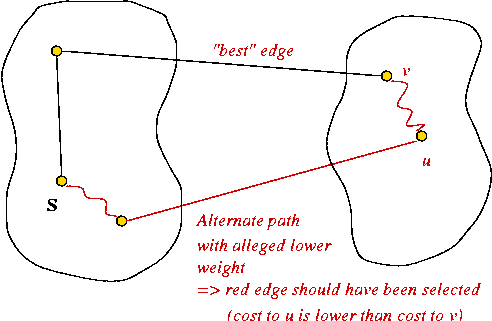
If a shorter alternate path existed, it would contradict the selection of the current path.

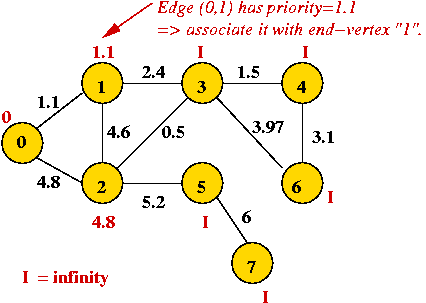
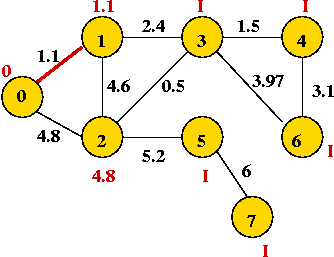
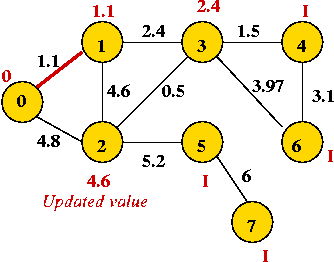
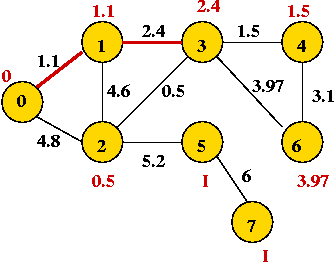
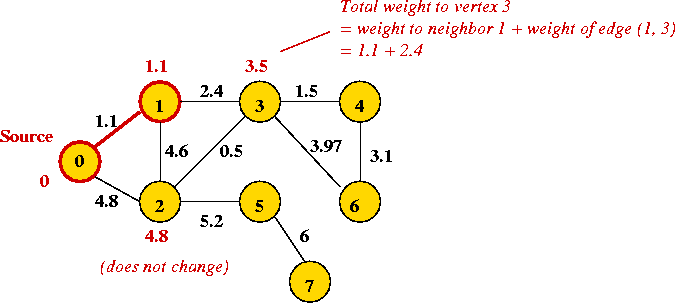
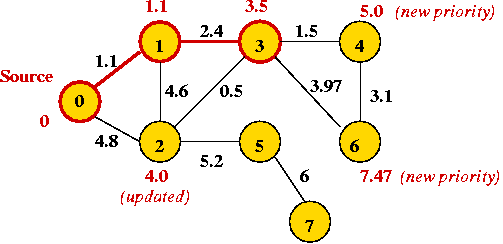
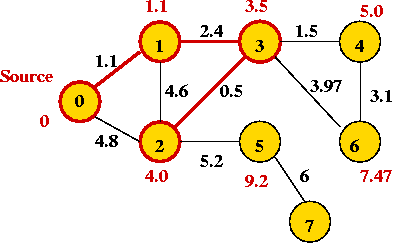
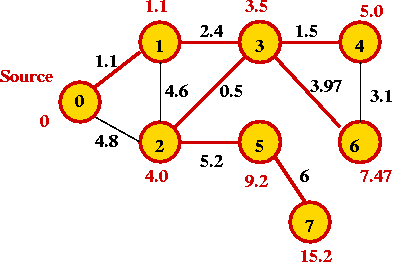
Example:

We'll find the Shortest Path Tree (SPT) rooted at vertex 0 (the source).

=> find shortest path from 0 to each vertex i.
Current SPT contains vertex 0.
Explore edges from most recently-added vertex (vertex 0):
Select vertex (outside SPT) with least weight (vertex 1), add it, and explore its edges:
Note:
- We associate with each vertex the total (currently-known) weight to the vertex from vertex 0.
- Let's call this value the "priority" of a vertex.
Add vertex with lowest "priority" value (vertex 3) and explore its edges:
Next vertex: 2
Continuing, we add: 4, 6, 5 and 7:

In-Class Exercise 8.8: Find the shortest path tree rooted at vertex 1 in this graph:

Implementation:

Key ideas:
- Again (as in Prim's MST algorithm), we associate a priority with each vertex.
- priority[i] = currently-known least-weight to i from source.
- Note: priorities change as vertices are processed
  => need decreaseKey operation.
- Use priority queue with extractMin and decreaseKey.

High-level pseudocode:


Algorithm: Dijkstra-SPT (G, s)
Input: Graph G=(V,E) with edge weights and designated source vertex s.

     // Initialize priorities and place in priority queue. 
1.   Set priority[i] = infinity for each vertex i;
2.   Insert vertices and priorities into priorityQueue;

     // Source s has priority 0 and is placed in SPT 
3.   priorityQueue.decreaseKey (s, 0)
4.   Add s to SPT;

     // Now process vertices one by one in order of priority (which 
     // may change during processing) 
5.   while priorityQueue.notEmpty()
         // Get "best" vertex out of queue. 
6.       v = priorityQueue.extractMin()
         // Place in current SPT. 
6.       Add v to SPT;
         // Explore edges from v. 
7.       for each neighbor u of v
8.           w = weight of edge (v, u);
             // If there's a better way  to get to u (via v), then update. 
9.           if priority[u] > priority[v] + w
10.              priorityQueue.decreaseKey (u, priority[v] + w)
11.          endif
12.      endfor
13.  endwhile

14.  Build SPT;
15.  return SPT

Output: Shortest Path Tree (SPT) rooted at s.

Details left out:
- Initializing of priority queue.
- Graph representation.
- Building SPT.
  To build, we'll record predecessor vertices (as we did for MST problem).

More detailed pseudocode: (adjacency matrix)


Algorithm: Dijkstra-SPT (adjMatrix, s)
Input: Adjacency matrix representation of graph, and designated source vertex s.

     // Initialize priorities and place in priority queue. 
1.   for i=0 to numVertices-1
2.     priority[i] = infinity
3.     insert (vertex i,  priority[i])
4.   endfor

     // Source s has priority 0 and is placed in SPT 
5.   priorityQueue.decreaseKey (s, 0)
4.   predecessor[s] = s

     // Now process vertices one by one in order of priority.
5.   while priorityQueue.notEmpty()
         // Get "best" vertex out of queue and place in SPT. 
6.       v = priorityQueue.extractMin()
7.       Add v to SPT;
         // Explore edges from v. 
8.       for i=0 to numVertices-1
             // If there's an edge and it's not a self-loop. 
9.           if i != v and adjMatrix[v][i] > 0
10               w = weight of edge (v, i);
10.              if priority[i] > adjMatrix[v][i] + w
                     // Set new priority of neighboring vertex i to total path weight 
11.                  priorityQueue.decreaseKey (i, adjMatrix[v][i] + w)
12.                  predecessor[i] = v
13.              endif
14.          endif
15.      endfor
16.  endwhile

17.  treeMatrix = adjacency matrix representation of tree using predecessor array;
18.  return treeMatrix

Output: Shortest Path Tree (SPT) rooted at s.

Sample Java code: (source file)


  public GraphPath[] singleSourceShortestPaths (int source)
  {

    // Create heap. Note: BinaryHeap implements the PriorityQueueAlgorithm 
    // interface (that has insert, extractMin and decreaseKey operations. 

    PriorityQueueAlgorithm priorityQueue = new BinaryHeap (numVertices);
    priorityQueue.initialize (numVertices);
    

    // Place vertices in priority queue. 

    GraphVertex[] vertices = new GraphVertex [numVertices];
    for (int i=0; i < numVertices; i++) {
      GraphVertex vertex = new GraphVertex (i);
      vertices[i] = vertex;
      if (i != source) {
        vertex.setKey (Double.MAX_VALUE);
        predecessor[i] = -1;
      }
      else {
        vertex.setKey (0);
        predecessor[i] = i;
      }
      priorityQueue.insert (vertex);
    }
    

    // Now process vertices one by one in order of priority (which changes 
    // during the course of the iteration. 

    while (! priorityQueue.isEmpty() ) {

      // Extract vertex with smallest priority value. 
      GraphVertex vertex = (GraphVertex) priorityQueue.extractMin ();

      // For readability we'll use these shortcuts. 
      int v = vertex.vertexID;
      double v_key = vertex.getKey();
      
      // Scan neighbors in adjMatrix. 

      for (int i=0; i < numVertices; i++) {

        // Look at row adjMatrix[v][i]. 
        if ( (v != i) && (adjMatrix[v][i] > 0) ) {

          // We have found a neighbor: relax the edge (v,i). 
          double w = adjMatrix[v][i];

          // If the current priority is higher, lower it via edge (v,i). 
          if (vertices[i].getKey() > v_key + w) {

            // decreaseKey operation. 
            priorityQueue.decreaseKey (vertices[i], v_key+w);

            // Record predecessor to build SPT later. 
            predecessor[i] = v;

          }

        }

      } //endfor 
      
    }
    

    // Next, we need to build the paths.  
    // ... (not shown) ... 

  }

Analysis:

Adjacency matrix:
- Initializations: all are O(V).
- There are V iterations of the while-loop.
- Finding the lowest-priority: O(log(V)) (scan of priority array).
- Scan of neighbors: O(V)
- Total work in while-loop: O(V²log(V))
- Note: just like in Prim's algorithm, a straightforward implementation (without a priority queue) takes O(V²) time.
Adjacency list:
- Each each is processed just once (when explored):
  => O(E) decreaseKey operations (worst-case)
  => O(E log(V)) time for all decreaseKey operations.
- Loop is executed O(V) times
  => O(V) extractMin operations
  => O(V log(V)) cost.
- Total time: O(E log(V)) + O(V log(V)) = O(E log(V)).

Importance of data structure (priority queue):

The priority queue allowed us to perform extractMin and decreaseKey relatively fast.
Implementation requires close-relationship between data structure and algorithm variables/data.
It is possible to separate, but adds cost (artificial separation).

Other (exotic) data structures

Data structure	extractMin	decreaseKey	Lines of code (C++)
Binary heap	O(log(V)) worst-case	O(log(V) worst-case	40
Pairing heap	O(log(V)) amortized	O(1) amortized	75
Binomial heap	O(log(V)) worst-case	O(log(V)) worst-case	84
Fibonacci heap	O(log(V)) amortized	O(log(V)) amortized	128
Self-adjusting binary tree	O(log(V)) amortized	O(log(V)) amortized	128
Relaxed heap	O(log(V)) amortized	O(1) amortized	177
Run-relaxed heap	O(log(V)) worst-case	O(1) worst-case	357

In practice, the binary-heap performs the best:
- O(log(V)) for decreaseKey is an overestimate.
  => most decreaseKey's cause only a few swaps.
- Array implementation of heap is very efficient.
- Array implementation (inadvertently) takes advantage of system caches.

Sparse vs. Dense Graphs

Recall the following execution-time analysis for Dijkstra's (or Prim's) Algorithm:

Adjacency-matrix version: O(V²).

Adjacency-list version (with priority queue): O(E log(V)).

Is O(E log(V)) always better?

Recall: O(V) <= E <= O(V²).
If E = O(V²), the graph is dense
many edges.
If E = O(V), the graph is sparse
few edges.
Now compare:

Dense Sparse

Adjacency-matrix O(V²) O(V²)

Adjacency-list O(V² log(V)) O(V log(V))
Thus, for dense graphs, the adjacency matrix is likely to better:
- Matrix operations are fast (array indexing is fast).
- Arrays can take advantage of architectural features (index registers, caching).

	Dense	Sparse
Adjacency-matrix	O(V²)	O(V²)
Adjacency-list	O(V² log(V))	O(V log(V))