Module 6: Odds and Ends

A Simple Exercise

In-Class Exercise 6.1: Download this template and solve the following problem. Suppose you are given a 2D array of integers and that each position in the array has the value 0 or 1. (Thus, a binary matrix). A sub-array of the matrix is considered a "chessboard" if the following properties hold: (1) the number of rows equals the number of columns (i.e. it is square); (2) there are at least two rows; (3) the 0's and 1's alternate as in a chessboard (i.e., none of the neighboring positions of a 0 has a 0). Your goal is to find the largest sub-matrix that is a chessboard. Analyse the complexity of your algorithm when the array size is N x N. Start by writing pseudocode.

Profiling

Most programming languages include supporting tools such as: (Java example)

A profiler

A Java profiling example:

A C profiling example:

How profiling works:

Beyond Profiling

Limitations of profiling:

Timing sections of code:

  • In Java: 
    
      long startTime = System.currentTimeMillis();

      // ... algorithm runs here ... 
      
      double timeTaken = System.currentTimeMillis() - startTime;

  • In C: 
    
#include <sys/times.h>

// NOTE: times.h may lie in different directories in some systems. 
// This example compiles on standard Linux distributions. 

static struct tms t_record; 

static double timer_start_time, timer_end_time;

void start_timer () 
{ 
  times (&t_record);
  timer_start_time = (double) (t_record.tms_utime + t_record.tms_stime);
}

double stop_timer () 
{ 
  times (&t_record);
  timer_end_time = (double) (t_record.tms_utime + t_record.tms_stime);
  return (timer_end_time - timer_start_time);
}

double timer_difference ()
{
  return (timer_end_time - timer_start_time);
}


int main ()
{
  double elapsed_time;

  // Start timing. 
  start_timer();

  // ... compute ... 

  // Get time taken. 
  elapsed_time = stop_timer();
}

System performance:

  • Generally, evaluating system performance is difficult.

  • Example:
    • A 3-tier system with front-end, middleware and back-end database.
    • Database may run on a multiprocessor.
    • Front-end and middleware may use different machines.
    • Where are the bottlenecks?

  • Modeling tools:
    • Develop analytic model of performance.
    • Solve model and try to predict worst-case performance.

  • Simulation:
    • Write (typically, discrete-event) simulation of system, leaving out unnecessary detail.
    • Run simulations under various application scenarios and data sets.
    • Identify bottlenecks.

Stepwise Refinement in Problem Solving

Stepwise refinement not only applies to coding, but also to problem-solving.

We'll use an example to illustrate: the maximal rectangle problem

  • Given: a 2D binary array (2D array of 0's and 1's).
  • Goal: find the largest sub-array (rectangle) consisting entirely of 1's.

First attempt: the obvious algorithm

  • Scan through array, stopping at each element.
  • Treat each element as a potential topleft corner of the rectangle.
  • For each such topleft corner, try all other elements as a potential bottom-right corner.
The code: 

public class NaiveMaxRect implements MaxRectangleAlgorithm {

  // ... 

  // See if the subrectangle (i,j,a,b) is filled with 1's. 

  boolean checkFilled (int i, int j, int a, int b)
  {
    for (int k1=i; k1 <= a; k1++) {
      for (int k2=j; k2 <= b; k2++) {
        if (A[k1][k2] == 0) {
          // Quit as soon as a zero is detected. 
          return false;
        }
      }
    }
    return true;
  }


  // Compute the area of rectangle (i,j,a,b) 

  int computeArea (int i, int j, int a, int b)
  {
    // Bad input: 
    if (a < i)
      return -1;
    if (b < j)
      return -1;

    // Area. 
    return (a-i+1) * (b-j+1);
  }


  // The algorithm. 

  public int findMaxRectangleArea (int[][] A)
  {
    // ...  
    
    // 1. Initialize. 
    int maxArea = 0;

    // 2. Outer double-for-loop to consider all possible positions 
    //    for topleft corner. 

    for (int i=0; i < M; i++) {
      for (int j=0; j < N; j++) {

        // 2.1 With (i,j) as topleft, consider all possible bottom-right corners. 

        for (int a=i; a < M; a++) {
          for (int b=j; b < N; b++) {

            // 2.1.2 See if rectangle(i,j,a,b) is filled. 
            boolean filled = checkFilled (i, j, a, b);

            // 2.1.3 If so, compute it's area. 
            if (filled) {

              // Check area. 
              int area = computeArea (i, j, a, b);
              
              // If the area is largest, adjust maximum and update coordinates. 
              if (area > maxArea) {
                maxArea = area;
                topLeftX = i;  topLeftY = j;
                botRightX = a;  botRightY = b;
              }
            }
          }

        } // end-3rd-for 

      } // end-2nd-for 
      
    } // end-outermost-for 

    return maxArea;
  }

  // ... 

}

Some improvements:

  • Check area first before scanning for 1's!
    => if area is too small, ignore rectangle.
  • Eliminate as many size-1 rectangles from search as possible.
  • Check corners for 0's before proceeding.
The code: 

  // ... 
  
  public int findMaxRectangleArea (int[][] A)
  {
    // ... 
    
    // 1. Check if array is all zeroes: this is O(mn) work. 
    boolean found = false;
    outer:
    for (int i=0; i < M; i++) {
      for (int j=0; j < N; j++) {
        if (A[i][j] == 1) {
          found = true;
          topLeftX = botRightX = i;
          topLeftY = botRightY = j;
          break outer;
        }
      }
    }

    // 2. If all zeroes, no further checks are required. 
    if (! found)
      return 0;

    // 3. We know there's at least one 1 x 1 rectangle (of area 1). 
    int maxArea = 1;

    // 4. Outer double-for-loop to consider all possible positions 
    //    for topleft corner. 

    for (int i=0; i < M; i++) {
      for (int j=0; j < N; j++) {

        // 4.1 With (i,j) as topleft, consider all possible bottom-right corners. 

        for (int a=i; a < M; a++) {
          for (int b=j; b < N; b++) {

            // 4.1.1 No need to check size-1 rectangles. 
            if ( (a == i) && (b == j) )
              continue;

            // 4.2.1 If a corner is zero, no need to check further. 
            if ( (A[i][j] == 0) || (A[a][b] == 0) )
              continue;

            // 4.2.2 First compute area to see if we should scan for 1's. 
            int area = computeArea (i, j, a, b);

            if (area > maxArea) {

              // 4.2.2.1 Only if area is larger should we bother checking. 
              boolean filled = checkFilled (i, j, a, b);
              if (filled) {
                maxArea = area;
                topLeftX = i;  topLeftY = j;
                botRightX = a;  botRightY = b;
              }
            } // endif-area 

          } // end-innermost-for 
          

        } // end-3rd-for 

      } // end-2nd-for 
      
    } // end-outermost-for 

    return maxArea;
  }

  // ...

Analysis (for both variations):

  • Suppose the array is m x n.
  • Each topleft corner visits about O(mn) locations.
  • For each such topleft corner, the bottom right corner visits no more than O(mn) positions.
  • An evaluation (checking for 1's) takes O(mn) in the worst-case for each rectangle checked.
  • Total: O(m3 n3) (worst-case).

Let's see if we can avoid some unnecessary comparisons:

  • Consider this example:


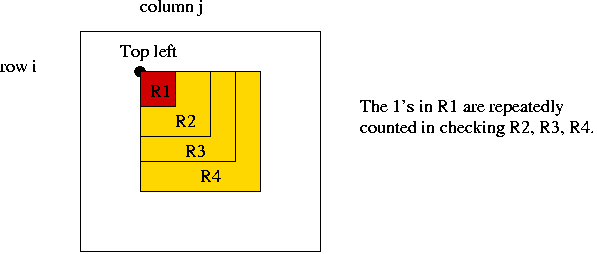
    => Small rectangles enclosed by larger ones are always scanned when processing the larger ones.

  • Use bottom up approach:

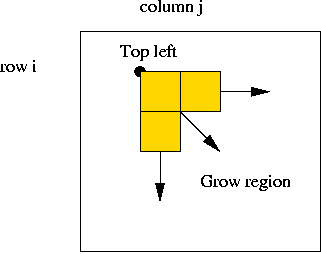
    • Start at topleft corner (i, j).
    • Grow region rightwards and downwards as much as possible.

  • A key observation:

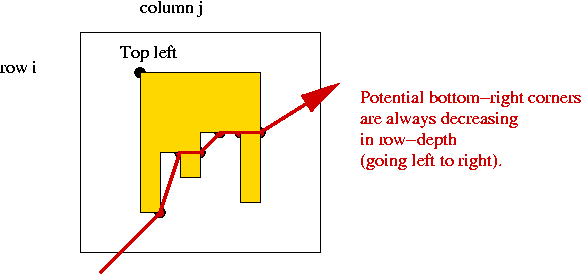
    • Consider potential bottom-right corners.
    • These form an ascending sequence right to left.
      => never need look "deeper" than in previous column.

  • Code: 
    
  // ... 

  // Start with top left at i,j and find largest rectangle of 1's. 
  // Use java.awt.Point to store and return two integers. 

  Point growRegion (int i, int j)
  {
    // 1. best_a and best_b will record the best bottom-right corner so far. 
    int best_a = i,  best_b = j;

    // 2. a and b will range over possible locations for the bottom-right corner. 
    int a = i,  b = j;

    // 3. There is no need to search below rowMax, which is updated 
    //    as we proceed. 
    int rowMax = M-1;


    // 4. Scan left to right along row i using index b as long as there are 1's. 

    while ( (b <= N-1) && (A[i][b]) != 0) {

      // 4.1 Start at the highest possible row, row i. 
      a = i;

      // 4.2 Descend into current column (column b) as far down as possible. 
      while ( (a <= rowMax) && (A[a][b] == 1) )
        a = a + 1;

      // 4.3 Back up to the last "1". 
      a = a - 1;
      
      // 4.4 Update rowMax if we stopped at an earlier row. 
      if (a < rowMax)
        rowMax = a;

      // 4.5 Check to see if found a larger rectangle. 
      int area = computeArea (i, j, a, b);

      // 4.6 If the rectangle is larger, update. 
      if (area > maxArea) {
        best_a = a;
        best_b = b;
        maxArea = area;
        topLeftX = i;  topLeftY = j;
        botRightX = best_a;  botRightY = best_b;
      }

      // 4.7 Continue with next column. 
      b++;

    } // endwhile 
    
    // 5. Return best bottom-right corner. 
    return new Point (best_a, best_b);
  }
  

  public int findMaxRectangleArea (int[][] A)
  {
    // ... 

    // 1. Check if array is all zeroes. 

    // ... 

    // 2. If all zeroes, no further checks are required. 

    // 3. We know there's at least one 1 x 1 rectangle (of area 1). 
    maxArea = 1;

    // 4. Outer double-for-loop to consider all possible positions 
    //    for topleft corner. 

    for (int i=0; i < M-1; i++) {
      for (int j=0; j < N-1; j++) {

        // 4.1 Find the largest possible rectangle with topleft at i,j. 
        Point p = growRegion (i, j);

        // NOTE: growRegion itself updates the current largest rectangle, 
        //       so there's no need to do it here. 
        
      } 
      
    } // end-outermost-for 


    // 5. Return value. 
    return maxArea;
  }

  // ...

  • Have we reduced the complexity?
    • Potential topleft corners: O(mn).
    • Each execution of growRegion is O(mn), worst-case.
      => O(m2 n2) overall.

An improvement:

  • As the top-left moves along a row, some columns are repeatedly scanned:

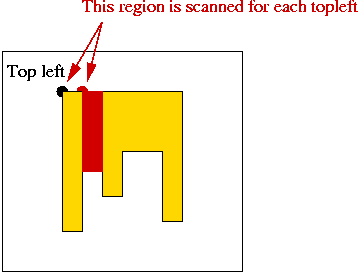
  • Idea:
    • We only need the number of 1's.
      => use a cache.

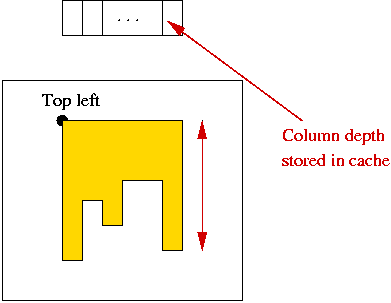
    • Pre-compute cache for each row before moving topleft-corner along row.

  • Code: 
    
  // ... 

  // Start with top left at i,j and find largest rectangle of 1's. 

  Point growRegion (int i, int j)
  {
    // 1. best_a and best_b will record the best bottom-right corner so far. 
    int best_a = i,  best_b = j;

    // 2. a and b will range over possible locations for the bottom-right corner. 
    int a = i,  b = j;

    // 3. There is no need to search below rowMax, which is updated 
    //    as we proceed. 
    int rowMax = M-1;

    // 4. Scan left to right along row i using index b as long as there are 1's. 

    while ( (b <= N-1) && (A[i][b]) != 0) {

      // Replace this: 
      //   a = i; 
      //   while ( (a <= rowMax) && (A[a][b] == 1) ) 
      //     a = a + 1;  
      //   a = a - 1; 
      // with: 

      // 4.1 Descend into current column (column b) as far down as possible - in time O(1)! 
      a = i + cache[b] - 1;
      
      // 4.2 Update rowMax if we stopped at an earlier row. 
      if (a < rowMax)
        rowMax = a;
      else
        a = rowMax;

      // 4.3 Check to see if found a larger rectangle. 
      int area = computeArea (i, j, a, b);

      // 4.4 If the rectangle is larger, update. 
      if (area > maxArea) {

        // ... 

      }

      // 4.5 Continue with next column. 
      b++;

    } // endwhile 
    
    // 5. Return best bottom-right corner. 
    return new Point (best_a, best_b);
  }
  

  // For each row, create the cache that's used repeatedly in the row. 

  void fillCache (int i)
  {
    // 1. Initialize, since cache is created just once. 
    Arrays.fill (cache, 0);

    // 2. Walk across the columns. 
    for (int j=0; j < N; j++) {

      // 2.1 For each column position (i.e., potential top-left corner), 
      //     find the longest column of 1's. 
      for (int a=i; a < M; a++) {
        if (A[a][j] == 0)
          break;
        else
          cache[j] ++;
      }

    } // end-column-scan. 

  }
  

  public int findMaxRectangleArea (int[][] A)
  {
    // ...  

    // Create space for cache - use maximum possible size. 
    cache = new int [N];

    // ... 

    for (int i=0; i < M-1; i++) {

      // Fill cache for row i. 
      fillCache (i);

      // Scan columns in row. 
      for (int j=0; j < N-1; j++) {

        // Find the largest possible rectangle with topleft at i,j. 
        Point p = growRegion (i, j);
        
      } 
      
    } // end-outermost-for 

    // ... 

  }

  // ...

  • Improvement in complexity:
    • We have reduced growRegion to O(n) (number of columns).
    • Overall: O(m n2).
    • However, we require O(n) additional space.

Note: the material on the maximal rectangle problem is based on an article by D.Vanderwoode in Dr.Dobbs Journal, 1998. Much of the code is completely re-written here (in Java).