Module 15: Loops II

Objectives

By the end of this module, you will be able to:

Demonstrate use of indefinite while loops with input inside.
Demonstrate ability to write code in equivalent loops (for-loop to while-loop and vice versa).
See examples of do-while, continue, and break.
Identify new syntactic elements related to the above.

A simple example

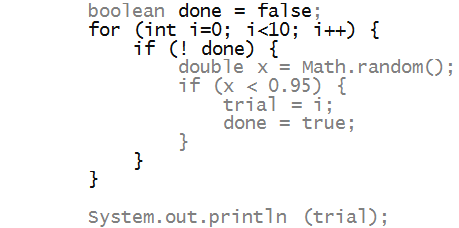
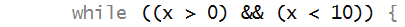Consider this simple problem:

We call Math.random() repeatedly.
Suppose we are interested in getting a number between 0 and 0.01. It might take several tries (calls to Math.random()).
The first trial is trial 0, the second one is trial 1, etc.
=> We'd like the trial # when we get our desired result.

Consider the following solution using a for-loop:

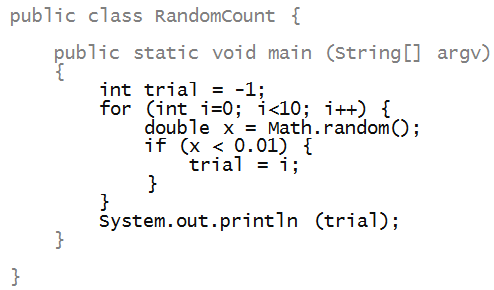
In-Class Exercise 1: Run the above program several different times (because the output is random). How many trials are needed to get a random number generated that's between 0 and 0.01? Add a println to print out each value of x generated.

In-Class Exercise 2: There is a problem with the above program. To see it, suppose we change the question to: how many trials are needed to get a random number generated that's between 0 and 0.95? Again, add the println so that you see each value of x generated.

To address the problem, we need stop updating trial once we get the first "hit"

We can do this using a boolean so-called "flag" variable:

Here, done is initially false.
The original body of the for-loop is now in an if-statement that tests done.
The code inside is executed only if done is false:
This way, when we want to not execute the code inside, we change done to true.
This way, the if-body does not get executed after that, even if the for-loop runs on.

In-Class Exercise 3: Again, add one println just inside the for-loop that prints the current values of i and done. Add another println inside the if so that each value of x generated is printed. Change 0.95 to 0.25. Then execute a few times to see how this is working.

Preventing further execution of the for-loop:

Is there a way to stop executing the remaining iterations of the for-loop?
We can do this using a break statement:
When the break executes, execution continues after the for-loop
=> It's a way to jump out of a for-loop.

In-Class Exercise 4: Try the above program to see that it works. Change the problem back to the first one, of seeing how many trials are needed to generate the first number less than 0.01. Again, add a println to print each generated value.

The problem we have not yet solved: what if the for-loop upper-limit is not enough?

To solve this problem, we will use a while loop:

Here, you can read the while statement as "as long as (x > 0.01)" ... (execute the loop body).

In-Class Exercise 5: Try the above program to see that it works. Again, add a println inside the loop at the end, to print each generated value.

Initialization for a while loop:

One has to be careful when initializing the variables that are tested in a while-loop.

Notice that the following would not work:

     int trial = 0;
     double x = 0;
     while (x > 0.01) {
         trial++;
         x = Math.random ();
     }
     System.out.println (trial);

Nor does

     int trial = 0;
     double x = Math.random ();
     while (x > 0.01) {
         trial++;
         x = Math.random ();
     }
     System.out.println (trial);

In-Class Exercise 6: Why not?

In the sequel, we'll look at some examples of both while-loops and the break statement.

Rules of thumb about which to use:

When you do NOT know the upper limit, use a while-loop.
When you do, prefer a for-loop (even though you can still use a while-loop).
If you need to stop the for-loop after some condition is true, then use break.

While-loop examples

Let's start with a simple one: what is the first square (of an integer) that is larger than 1000?

To solve this, we'll use this high-level idea:

     1.  Start with i = 1.
     2.  Check whether i*i > 1000.
     3.  If not, increment i and repeat.

Here's the while-loop:
Since we know that i can never be larger than 1000 itself, we could use a for-loop with a break:

In-Class Exercise 7: Although it's more complicated, as an exercise, rewrite the above using a for-loop but without a break.

Next, let's return to the square-root computation from Module 11.

Suppose we want to compute the square root of a number a.

Recall the idea:

     1.  Start with a guess x.
     2.  Improve the guess to x = 0.5*(x + a/x)
     3.  Repeat.

How much repetition? We should stop when we've reached some desired accuracy.
Here's one way:
Notice the while-condition:
You can read this as "As long as the difference between x*x and a is larger than 0.000001, continue iterating".
Now, such a condition will not work if we are finding the square root of very small numbers.

In-Class Exercise 8: Why not?

To address this problem, one could stop when the percentage (or fractional) difference between two successive iterates is small enough.
Here's one way of writing the code:

In-Class Exercise 9: Rewrite the above to use a for-loop with a break.

Consider the one-dimensional random-walk problem:

A particle starts at the point (5,0) on the x-axis.
At each step, it either moves left or right, choosing randomly.
When the particle reaches either the origin (0,0) or the point (10,0), it stops.
The obvious question: how many steps (moves) until it stops?
It'll take at least 5 steps, but it could take an unknown (large) number of steps.
=> An obvious candidate for a while-loop.
Consider the following program:
Notice that the while-loop condition is an AND-combination:
Both x>0 and x<10 need to be satisfied to continue executing inside the while-loop.
Here, we have used a random number between 0 and 1 to decide which way to go.
=> Half the time we will move right because half the time, a random number will be less than 0.5.

In-Class Exercise 10: Modify the above code so that you also detect which "boundary" the particle hits (0 or 10) when it stops, and print it out. Include a println inside the while-loop to print the current value of x so that you see how it's changing.

Next, let's estimate the average number of steps it takes to stop:

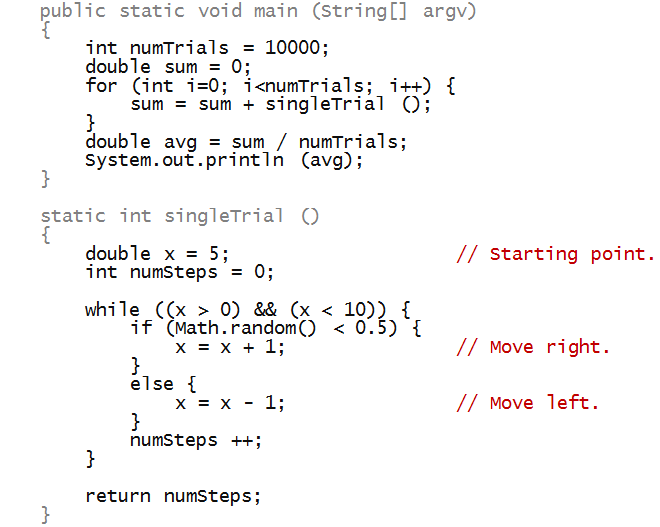
In-Class Exercise 11: Why is a for-loop used in main instead of a while-loop? Just to see how it would work, re-write the loop in main to use a while-loop. What is the average number of steps reported?

The above idea generalizes quite easily to two dimensions:

Here, we'll place a particle at location (5,5) and let it wander randomly (on integer coordinates).
The particle stops when it hits the walls of the box with corners (0,0) and (10,10).
How does the particle move? With equal probability it moves up, down, left, or right.
=> Since there four possibilities, each occurs with probability 0.25.
To decide, we'll draw a random number between 0 and 1:
- If the number is between 0 and 0.25, move north.
- If it's between 0.25 and 0.5, move south.
- If it's between 0.5 and 0.75, move east.
- Otherwise, move west.
Here is the structure of the while-loop

In-Class Exercise 12: Add the missing lines of code to determine the new values of x and y in the loop. Then, estimate the average number of steps over 10,000 trials.

Try this exercise:

Write down a large number (many digits). Call this k.
Compute k % 10 and write down that number.
Then, set k = k/10 using integer division.
Repeat.

Let's put this into a program:

The program extracts the digits from a number to form a String.
Notice how the string concatenation is done.

In-Class Exercise 13: Rewrite the program using a for-loop.

Examples with break

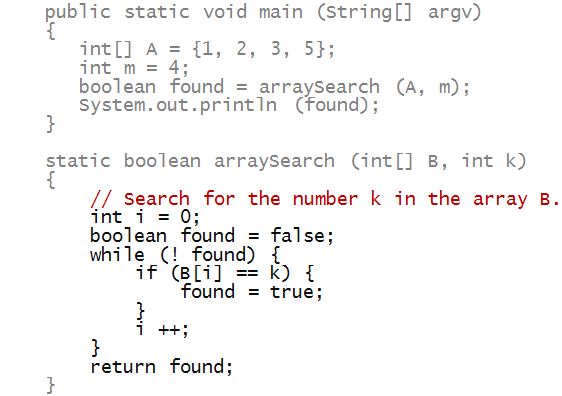
Consider this problem:

We are given two arrays A and B.
For each element in A, we are to see if it occurs in B, and if it occurs, report the position in the array where it occurs.

Thus, for the arrays

	int[] A = {1, 9, 16, 25, 36, 49, 64};
	int[] B = {2, 4, 8, 16, 32, 64};

we need to report something like

    A[2] found at position=3 in B
    A[6] found at position=5 in B

Here's the program:
The rule with break - when executed, it "breaks" out of the nearest enclosing for-loop:
Notice that the break is itself inside a conditional
=> The break can be deeply nested inside a loop.

In-Class Exercise 13: Add a println just inside the outer for-loop to print i, and one just inside the inner for-loop to print j. Trace the program's execution.

In-Class Exercise 14: Suppose we were to solve this variation of the problem: given the two arrays, see if an element in A occurs in B and if it occurs, print the position. Thus, we only need one element to satisfy this. Modify the program, adding a break to make this work.

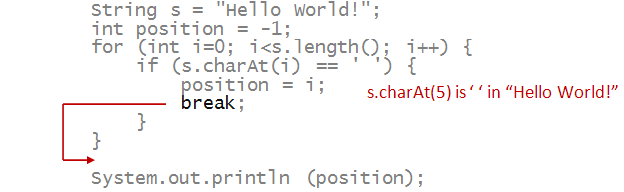
Here's another simple example:

Suppose we examine a string to locate the position of the first blank. If there are none, we print -1
The break gets executed when i is 5:
Consider this while-loop version:

In-Class Exercise 15: Why doesn't this work? Can you tell just by reading?

In-Class Exercise 16: Suppose you changed initial value to position = 0 outside the while-loop. Does it work?

Infinite loops

Consider this programming error:

Here, we mistakenly forgot to increment i inside the loop.
=> The loop test is always true.
In this case, execution continues forever.

In-Class Exercise 17: Don't believe it? Try it!

Here's another example of an error that leads to an infinite loop:

Generally, one should be careful with equality (or not-equal) tests in while-loop conditions.
The following inequality, even if not ideal, works:

In-Class Exercise 18: Does the following lead to an infinite loop?

Odds and ends

We'll now look at a few less frequently used features related to loops:

There is a version of the while loop called a do-while:
Here, execution enters the loop directly from above, without any condition tested:
As long as the condition holds, execution continues inside the loop:
A related statement to the break statement is the continue statement:
When continue is executed, execution goes back to the top of the loop:
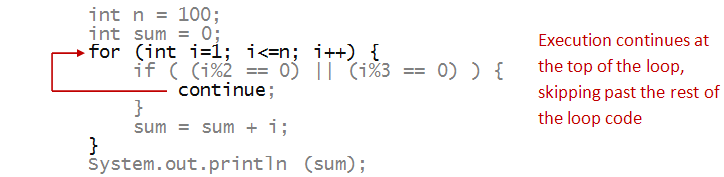
This is sometimes useful when the rest of the loop has complex code. (The above example does not.)

When things go wrong

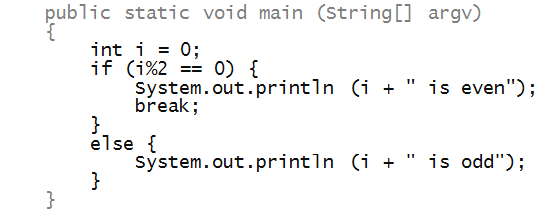
In-Class Exercise 19: What is the error in this program?

In-Class Exercise 20: This program seeks to sum the elements of an array. What is the error in the program?