Module 11: Science & Engineering Applications II

Objectives

By the end of this module, for simple programs with real numbers, you will be able to:

Apply arrays to scientific applications like vector addition and multiplication;
Be able to extract simple stats from data in an array: mean, variance;
Be able to optimize using gradient descent;
Be able to apply Newton's method to finding square-roots.

Simple statistics

Let's use what we know in programming to explore some statistics.

First, some definitions:

Suppose we have n pieces of data (real numbers):
a₁, ..., a_n
The sample mean of this data is defined as:
m = (a₁ + ... + a_n) / n
That is, sum them up and divide by the number of data.
The mean, a measure of "centrality", is one short way to characterize data.
Once the mean has been calculated, compute the sample variance as:
v = ( (a₁ - m)² + ... + (a_n - m)² ) / (n-1)
Variance is a measure of "spread". Generally, the more the variance, the more the spread around the mean.
Define the median as follows:
- Sort the n pieces of data.
- Pick the middle value:
  - If n is odd, then the median is the (n+1)/2-st value in sort order.
  - Otherwise, the median is the average of the two middle values.
The median is an alternative measure of centrality.
The mode of the data is a little more complicated:
- First, divide the range into K equal-sized subintervals.
  e.g., if the range is [0,10] and K=5n, we could use the sub-intervals [0,2], [2,4], ..., [8,10].
- Compute, for each subinterval, the number of data values that lie in the sub-interval.
- The mode is the sub-interval with the most data values.
The mode is also a measure of centrality.

In-Class Exercise 1: Consider this data:

	0.9, 8.88, 1.9, 6.0, 3.9, 2.4, 0.3, 2.1, 9.6, 2.33, 7

Compute by hand (calculator) the mean, variance, median, and mode (using 5 intervals).

In-Class Exercise 2: Consider this data: Add one more piece of data to the above list so that the resulting mean is twice the original mean. What is the implication? Would the same thing occur with the median?

Next, let's write programs to compute these when the data is in an array:

Here's a calculation of the mean and variance:
To compute the median, we'll need to sort the data first:

In-Class Exercise 3: Explain the array indices above. Why do they work? Why doesn't (n+1)/2 work as the index inside the if-block.

Finally, the mode:

In-Class Exercise 4: Trace through the above program.

In-Class Exercise 5: Follow instructions in class to obtain a new data set. Then, use this data set to compute the mean, variance, median and mode. What is the size of the variation relative to the mean?

In-Class Exercise 6: The above data set has two variables. Plot one against the other using DrawTool.java. Is there a strong relationship?

Finding square roots

We'll now see how a simple idea leads to a program for computing the square root of a number:

The general idea is this:

       1.  Start with some guess
       2.  Do a calculation to improve the guess
       3.  Repeat

Example: suppose we are finding the square root of 9.
- Start with a guess, let's say, 2.
- Compute 9/2 = 4.5.
- Clearly, 2 is too small, and 4.5 is too big.
- The next guess should be between 2 and 4.5.
- A simple idea: take the average (2 + 4.5)/2 = 3.25.
- Now, compute 9/3.25 = 2.77 and repeat.

In-Class Exercise 7: Continue this iteration for two more steps. Try the same procedure on 25 with initial guess 2.

Let's put this idea into a program:

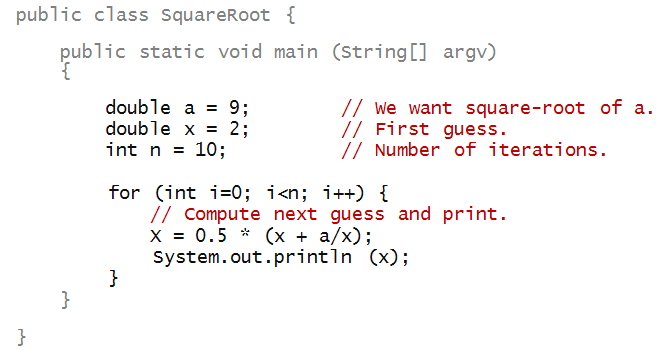
In-Class Exercise 8: Implement the above program and confirm your calculations for 9 and 25.

In-Class Exercise 9: Does the same idea work for cube roots? Suppose x is our current guess and that the next guess is an average between the the current guess x and something. What should the something be? What is the analog of a/x for cube roots?

In-Class Exercise 10: Write a program called CubeRoot to implement the above idea.

A more general iterative method

The problem of finding roots is a special case of a more general problem:

Finding the square root of 9 is the same as solving the equation x² = 9.
Which is the same as solving the equation x² - 9 = 0.

In-Class Exercise 11: Express the problem of finding the cuberoot of 27 in the manner above.

Zero-finding:

The more general problem: given a function f(x), solve f(x) = 0.

In-Class Exercise 12: Why zero? Why isn't solving f(x)=c for some constant c just as important a problem?

Consider this example:
f(x) = 2x³ - 5x² - 8x - 200

We'll consider the function over the range [0,9].
We'd like the value of x such that f(x) = 0.
This is what it looks like:
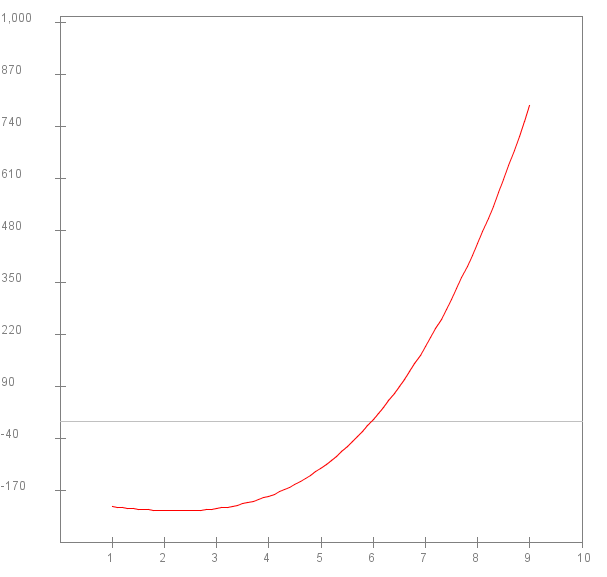
What we would like is an iterative approach similar to finding the square root:
- Start with an initial guess.
- Find the next guess.
- Repeat.
This is the idea we will use:
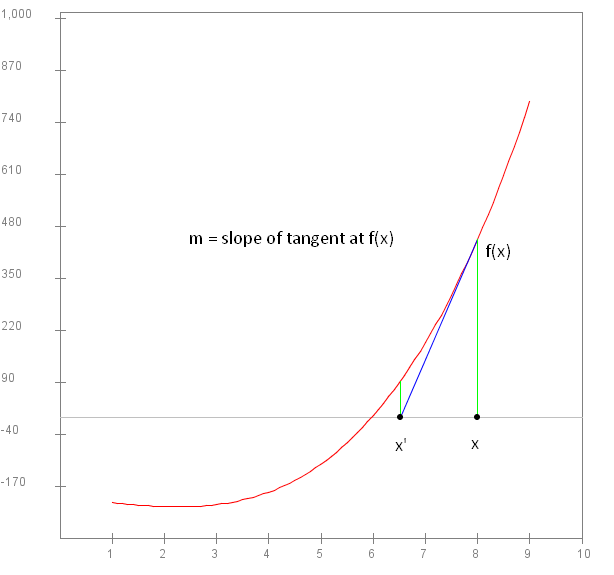
- Consider the curve f(x).
- Start with a guess x.
- Examine the tangent to the curve at the point (x, f(x)).
- This is a line.
- The line cuts the x-axis at x'.
- x' is the next guess.

In-Class Exercise 13: Suppose the slope of the tangent at the point (x, f(x)) is m. Express x' in terms of x, f(x), and m.

Next, let's focus on computing the slope of the tangent:

We are going first approximate the slope, and then think about how to compute it exactly.
To approximate the slope a tangent line, we'll use this idea:
- A curve will look like a line if you "zoom" in close enough.
As an example, consider the starting point x=8 for the above curve.
Let's zoom in on the curve in the region of x=8:
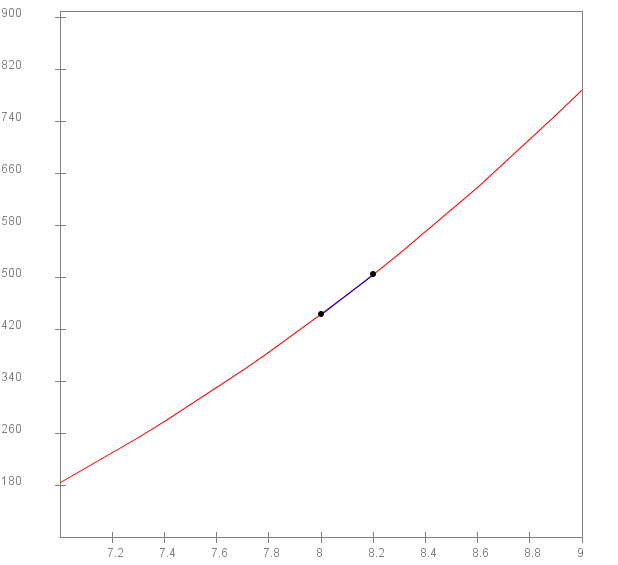
Now consider another point close by on the curve: (x₂, f(x₂)).
- In the above picture, x₂ = 8.2.
- The line between (x,f(x)) and (x₂, f(x₂)) is approximately aligned with the tangent.
- Thus, the slope of the line between (x,f(x)) and (x₂, f(x₂)) should be approximately the slope of the tangent.

In-Class Exercise 14: What is the slope of this line segment? Recall that the function is:
f(x) = 2x³ - 5x² - 8x - 200

In general, instead of the "close by" point 8.2 (which we think of as 8 + 0.2), we could pick any point 8 + Δ where Δ is a small number relative to 8.

In-Class Exercise 15: Write a small program to compute the slope of the function f(x) = 2x³ - 5x² - 8x - 200 by filling in code here:

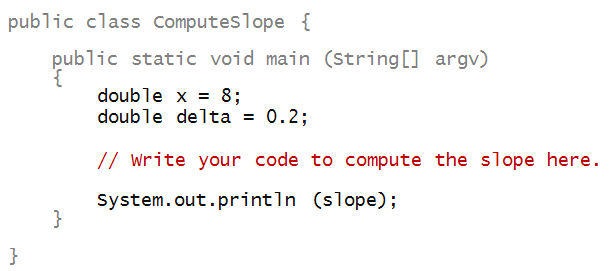
Next, let's put these ideas into a program that iteratively computes the next guess:

In-Class Exercise 16: What is the x value the iteration appears to converge towards? What is the value of f(x) at this x value?

Computing the tangent exactly:

Thus far, we have approximated the slope of the tangent.
One wonders: can it be computed exactly?
The answer is yes for many, many functions.

In-Class Exercise 17: Consider the function f(x) = 3x² + 4. Let Δ be some number. What is the slope of the tangent at x in terms of x and Δ?

In-Class Exercise 18: What happens in the above case when Δ is approximately zero? That is, what is the true slope of the tangent at x?

Let's return to the function
f(x) = 2x³ - 5x² - 8x - 200

It turns out that, if you do the algebra, the slope of the tangent at x is
tangent-slope = 6x² - 10x - 8
There is a (possibly different) tangent-slope at every possible x.
=> This is a function.
Thus, we can give this function a name:
g(x) = 6x² - 10x - 8
This function is called a derivative.
The more conventional way of naming the derivative:
f'(x) = 6x² - 10x - 8
Read this as "f prime x"
There are techniques for calculating the derivative
=> This is what you study in calculus.
Note: the inexact slope estimate we first used (with a fixed Δ) is called a finite-difference approximation of the derivative.

In-Class Exercise 19: Use the above derivative instead of the approximate slope in the iteration.

Summary:

To solve the problem f(x) = 0, we first derive the derivative f'(x).
Then, we iterate as follows:
x = x - f(x)/f'(x)
Sometimes, for clarity, we can write the (n+1)-st iterate in terms of the n-th one:
x_n+1 = x_n - f(x_n)/f'(x_n)
This is the way mathematicians describe this iteration, and is probably how Isaac Newton described it when he devised the method.
Newton's method is a very useful technique, used widely in science and engineering.

Recall that, computing the square root of a number a is the same as solving the equation x² - a = 0.

In-Class Exercise 20: Use the Newtonian method to derive an iteration for computing the square root. Compare this with the simple averaging procedure from earlier.

In-Class Exercise 21: Use the Newtonian method to derive an iteration for computing the cube root. Compare this with the simple averaging procedure from earlier.

In-Class Exercise 22: Write a program that computes the cube root using both approaches - the simpler averaging approach from earlier and Newton's iterative approach. Print the iterate at each step. Which one converges faster?

Applying derivatives to optimization

The general goal in optimization:

There is some function f(x) of interest.
We need to find the minimum or maximum value of f(x).
This problem has scores of applications in science and engineering.

Let's start with an example:
f(x) = 20 + 100(x³ - x²)
in the range [0,1].

Here's the function:
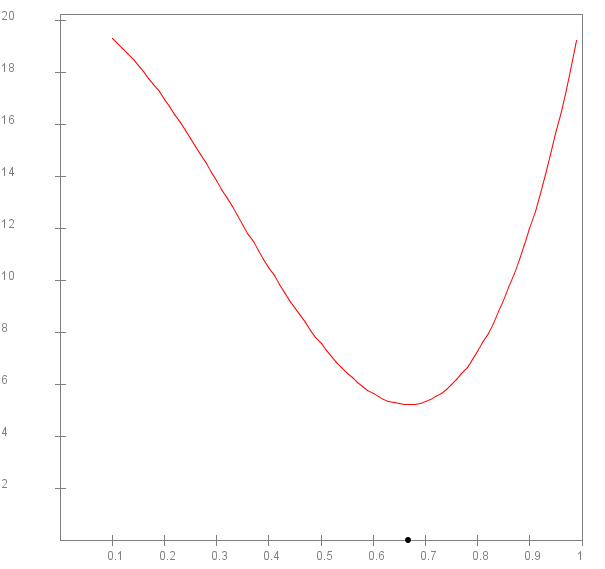
The x value where the minimum occurs is shown above.

In-Class Exercise 23: What is the tangent-slope (i.e., derivative) at the minimum?

Let's now try to identify the minimum:

Let's try a simple idea:
- Try different values of x.
- Pick the one with the tangent-slope closest to zero.
We'll use a finite-difference approximation of the derivative.
Here's the program:

In-Class Exercise 24: Execute the above program. What is the best slope reported? Then, change the search granularity to get a better estimate of the x value where the minimum occurs.

In-Class Exercise 25: Why is the first if-condition there? What happens when you take it out?

In-Class Exercise 26: The above program used a finite difference approximation for the tangent slope. Write down the derivative function when
f(x) = 20 + 100(x³ - x²)
Then, use the derivative f'(x) instead of the approximation in the program above.

In-Class Exercise 27: Clearly, the derivative f'(x) needs to be zero at the minimum. Can you solve this by hand by setting f'(x)=0?

A few comments about optimization:

Optimization is a big subject in itself, the topic of many books and much research.
=> We have only glimpsed at one optimization problem.
Recall that solving f'(x)=0 is a way to find the minimum.
- This can be done using Newton's iterative method.
- Newton's method was designed to solve g(x)= for any function g.
There are more sophisticated ways of setting up iterations to solve for the minimum.
- For example, here's a simple one:
  x = x - α f'(x)
- Can you see the intuition behind this?

Perfect numbers

Let's return to the mathematics of numbers, number theory, and write a program to find perfect numbers.

A perfect number, as defined by the Greeks, is a number whose divisors (other than itself) add up to the number.
Example: 6
1 + 2 + 3 = 6
Another example: 28
1 + 2 + 4 + 7 + 14 = 28
A program to check whether n is perfect:

In-Class Exercise 28: Modify the above program to identify all the perfect numbers between 1 and 10000.

In-Class Exercise 29: Modify the above program to sum up the reciprocals of the divisors for a perfect number. What do you observe? (Note: the reciprocal of a number a is 1/a).