Module 12: Methods II

Objectives

By the end of this module, for simple programs, you will be able to:

Trace the execution, mentally and written, of programs that have methods with integer/double parameters and return values.
Write methods to achieve the desired output.
Use method calls in expressions.
Explain the difference between basic-type parameters, and array parameters.
Debug errors in methods.
Identify new syntactic elements related to the above.

A long program

Let's write a program to compute the negative exponential function f(x) = e^-αx

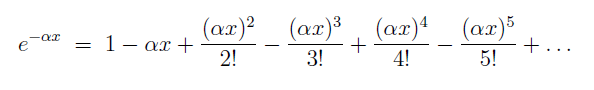
Here, α is a real number, a parameter of the function.

The program:

In-Class Exercise 1: Trace the program and output when x=1 and n=1.

Let's point out a few things about the above program:

It has triply-nested loops.
There are at least three things "going on" in the program:
- There's the outer loop that computes the function for different values of x
- There's an inner loop that computes the k-th term in the sum.
- The innermost loops compute the power and factorial functions.
All three are conceptually different, but come together in the program.

We will now re-write the program using methods for these conceptually different aspects of the program:

Here, we have defined a method called power:
And invoked the method from main:

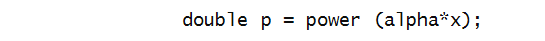
Here's yet another rewrite of the program:

Notice how much more readable this is.
For instance, look at the loop in main:
It's much more clear that x is being varied, and being used in a calculation done by the method negativeExponential.

It is easy to now add drawing or plotting without needing to understand anything beyond what's in main.

In-Class Exercise 2: Without typing up the program, merely write down how you would use DrawTool to plot the function. That is, write down the code in main and show where you would insert the drawing commands.

Why methods are useful:

They improve readability.
They can be used in multiple ways
=> e.g., the power method can be used for other functions.
They can be designed for use by other people.
=> e.g., the power method can be used in other people's programs.
Most importantly, they can be used in composition: methods that call methods that call methods ... and so on.

Before continuing, let's review methods as described in Module 4.

Method parameters

To see how methods work, let's start with a simple example:

In-Class Exercise 3: Edit, compile and execute the above program. Then, just before the declaration of j but after the first invocation of incrementAndPrint in main, print the value of i.

Let's examine method parameters step by step:

First, method names are like variable names: usually a collection of letters and numbers.
=> e.g., incrementAndPrint.
The capitalization inside the name (incrementAndPrint) has no effect on the compilation/execution
=> It's merely for readability.
Next, let's distinguish between invocation
and definition:
Let's focus on as few aspects of the definition.
When you read this, say to yourself
- "The method takes one parameter, an integer."
- "The method returns nothing" (void).
Next, let's examine the flow of execution with the first invocation:
At the next invocation:
What's important to remember: the value in j gets copied into the parameter variable k.
=> Thus, the value in j is not affected inside incrementAndPrint.
It's possible to use the same name for the parameter variables, even though they are different:
Here, we say that the scope of the variables i and j in the method incrementAndPrint is limited to all the code inside the method.

In-Class Exercise 4: Fill in the code in the method below so that the output of the program is:

  *****
  ***
  *

Multiple parameters

Consider the following example:

Here, the method checkPythagoreanTriple is defined with three parameter variables.
=> All happen to identically be int's but don't have to be.
The values at the invocation are given to the method in the order the parameters are declared:
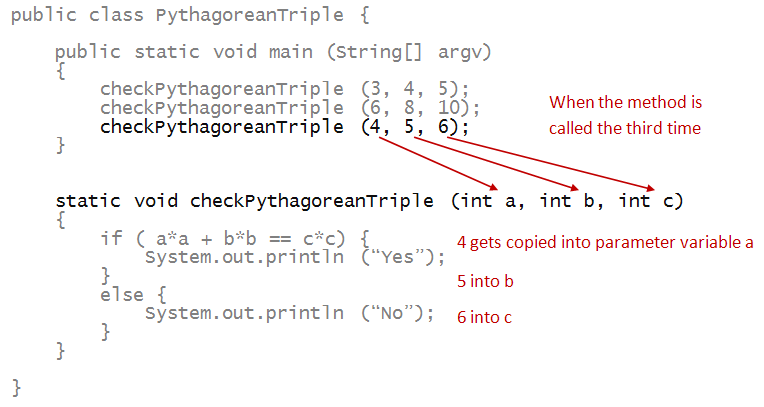
- The first value in the invocation goes to the first parameter variable.
- The second value in the invocation goes to the second parameter variable.
A method can be invoked in various ways:

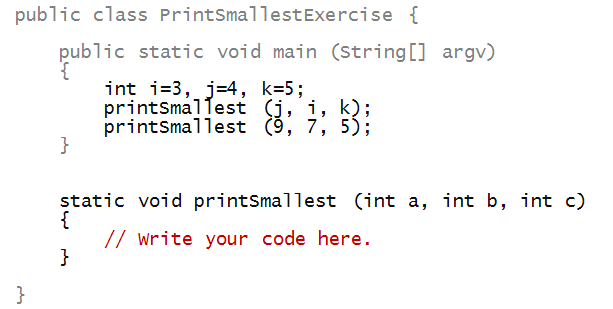
In-Class Exercise 5: Fill in the code in the method below so that the output of the program is 3 and 5, respectively.

Return values

So far, we've written methods that take values, do things and print.

We get a whole new level of programming power, when methods can compute something and return something to the invoker.

Here's an example:

To see how this works, let's simplify the program a little:
- Initially, a has the value 0.
- Then, the next thing to execute is the invocation to power.
- Only after power completes execution, does the assignment to a occur.
After power completes execution, the return value (8 in this case), gets assigned to a.

In-Class Exercise 6: Fill in the code in the method below so that the output of the program is 3 and 5, respectively.

Using method calls in expressions

Methods that return values can be used and combined in expressions, in powerful ways.

For example:

In the first statement, power gets called twice:
- The first time, it is with parameter values 2 and 3.
- The second time with parameters 2 and 4.
- The resulting expression is evaluated and the final result stored in a

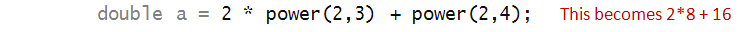
In-Class Exercise 7: Trace through the second expression above, when b is assigned a value. How can you determine the order in which power is called?

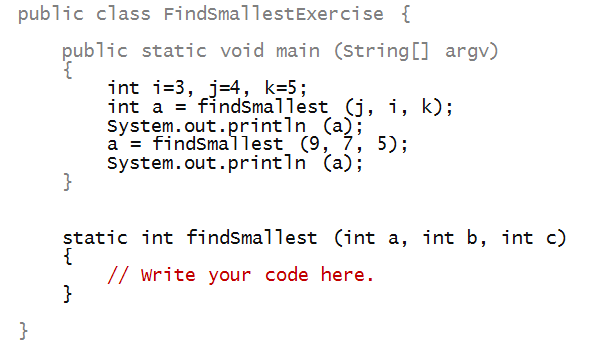
In-Class Exercise 8: In an earlier exercise, you wrote a method to find the smallest among three values. Suppose you had to find the smallest among five variables. Invoke the the method (with the three variables) twice to find the smallest among five. Fill in your code below:

Methods and arrays

When working with arrays, it's often useful to have some computations delegated to methods.

For example:

In-Class Exercise 9: Modify the above program to compute the mean of the array's elements.

A method can return an array:

In-Class Exercise 10: Without typing up the above program, trace through and describe what gets printed.

Let's point out a few things:

Notice how the return type is declared in the method definition:
This means that, inside the method, we need to return the same type of variable:
Each call to makeConsecutiveIntegers creates a fresh array:
- The size-5 array is "alive" until the second call to makeConsecutiveIntegers.
- After the second call returns, the variable A refers to the newly return (3-element) array.
If we had wanted to keep both arrays around, we'd write:
We can re-use a variable name inside a method:
Here, the scope of A inside makeConsecutiveIntegers is limited to all the code inside the method.
The two A variables in the program are really different variables.

Multiple returns in a method

Consider this example:

Observe that the min method has two return's.
Only one return is executed in any one invocation of a method, e.g.

In-Class Exercise 11: Trace the execution of the above program. Why does it work (that is, why does it find the minimum element in the array)? How often is the first return in min executed? How often is the second one executed?

Here's another example with multiple return's

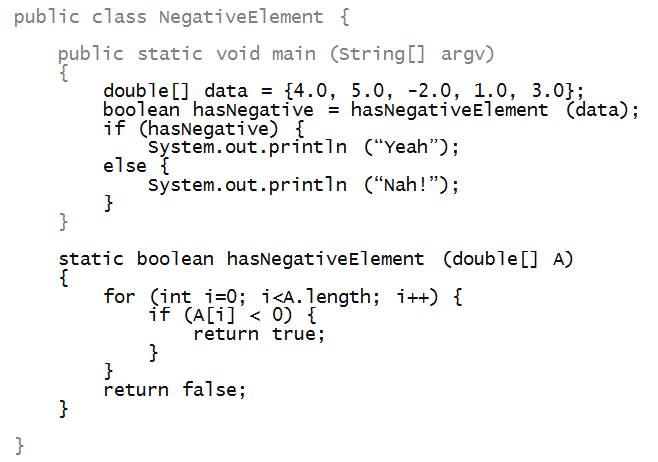
In-Class Exercise 12: Trace the execution of the above program. How often is the second return in hasNegativeElement() executed?

Let's point out a few things regarding the above program:

First, we could "compact" the code in main by writing:
This is possible because the return value of hasNegativeElement is Boolean, i.e., will result in true or false.

In-Class Exercise 13: Rewrite the hasNegativeElement method so that there is only one returnin it.

Call-by-value vs call-by-reference

Consider the following program:

In-Class Exercise 14: Before executing the program, guess the output. Then, edit, compile and execute to see what the output is.

To explain what happened, let's simplify a little:

First, consider this simple program:
Here, the value in a is copied into the parameter variable x.
This type of parameter behavior is called call-by-value:
=> The "value" is what's passed in a method "call"
Call-by-value applies to parameters of basic types like int and double.
Arrays, however, are treated differently.
Consider the same example for arrays:
Here, a "reference" (as it's called) is passed:
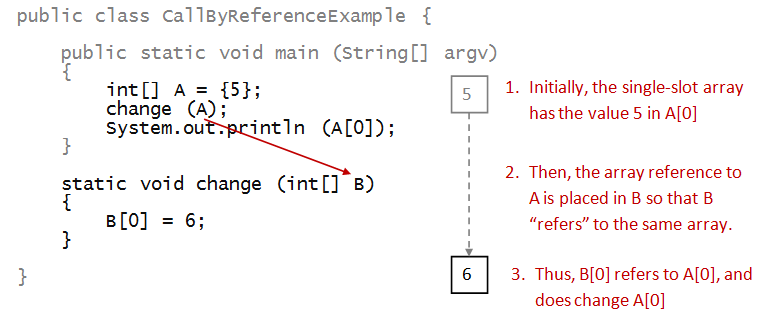
- A reference allows a method to modify the original.
- Yes, it's a little strange.
This parameter behavior is called call-by-reference
=> It applies to arrays, and more generally objects.
We will learn about objects (which are a special type of Java construct) later.

Finally, let's look at this program:

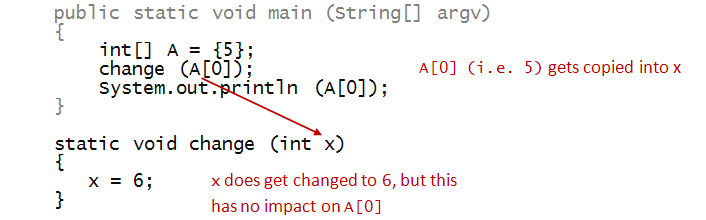
Here, we are NOT passing the array itself.
We are passing a single element of the array, an integer.
Because it's an integer, it gets copied into the parameter variable.
Thus, a change to x has no impact on the array.

Java's Math library

The term library is often used to describe a collection of useful, related methods.

Java has several such libraries, one of which is a collection of standard math functions.

Here's one example

Notice that the sqrt method is accessed from the Math package using the "dot" operator:
This will be true for all the math function in the Math package, e.g., e^x:
Think of the "dot" operator as "containing", as in "Math contains the sqrt".
Or think of it as "belonging", as in "sqrt, which belongs in the Math collection".
We can use these methods in expressions, as in:

Here are more examples of math functions in Math:

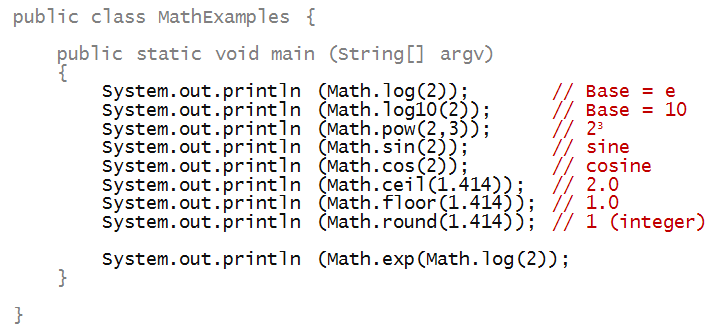
In-Class Exercise 15: What does the last line print?

In-Class Exercise 16: Use Math methods to compute sin²(x) + cos²(x) for any x. Do you know what you should get? Try different values of x. Can you prove this result? [Hint: use Pythagoras' theorem]

In-Class Exercise 17: Write a program called ZenoSum that uses Math.pow to compute the sum 1 + 1/2 + 1/4 + 1/8 + ... + 1/2ⁿ and then report what you get for a few different values of n such as n=5, 10, 15.

Let's plot the sin function in the range [0,2π]:

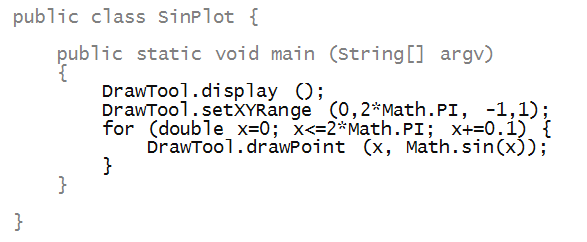
The Math library also has a few constants such as Math.PI and Math.E.

In-Class Exercise 18: Edit, compile and execute the above program.

In-Class Exercise 19: Using DrawTool with x-range [1,10] and y-range [0,1000], plot the following functions in different colors:

f(x) = x.

f(x) = x².

f(x) = log(x).

f(x) = exp(x).

f(x) = 2^x.

Which of these is the fastest growing? The slowest?

In-Class Exercise 20: What is an example of a function that grows faster than a^x no matter how big a is (here, a is a real number).

In-Class Exercise 21: Can you think of a function that grows slower than log(x) no matter what the base is? Plot this function along with log(x). (Change the y-range to show both more clearly.)

The Math.random method:

A call to Math.random returns a random value between 0 and 1.
For example, the following produces 10 such random values:

In-Class Exercise 22: Compute the mean and variance of the values. What do you get? Increase n to 1000 and compute mean and variance.

Next, let's examine these random values visually by plotting the points:
Similarly, one can plot points by choosing both x and y values randomly:

In-Class Exercise 23: Increase n to 100 and plot (x,y) points to see that random points fill up the space randomly but uniformly (without clustering in one place). Then, change the code to include animation:

        DrawTool.display ();
        DrawTool.setXYRange (0,1, 0,1);
	DrawTool.startAnimationMode ();
        int n = 10;
        for (int i=0; i<n; i++) {
            double x = Math.random ();
            double y = Math.random ();
            DrawTool.drawPoint (x, y);      
	    DrawTool.animationPause (500);
        }
	DrawTool.endAnimationMode ();

In-Class Exercise 24: Modify the code above to generate and plot 100 points that are randomly distributed in the range [0,10] (on the x-axis) and [20,30] on the y-axis. Change the XY-range in DrawTool accordingly.

Reading and writing

First, reading.

Consider this snippet of code:

When reading a method call, do not at first chase down the method to look at its body.
Instead, merely ask:
- What does the method take as parameters?
- What does the method return?
Here, we can tell that the parameters must be double's:
Although: we probably don't know the parameter variable names.
Similarly, we can tell what the return type must be:

Let's look at a method declaration:

Here, without knowing anything about how the method works, we can see how it needs to be called, e.g.,
Of course, the method code now must return an array:

Next, writing.

The following examples show various writing styles.
Most commonly used: one or two spaces (in the Math.sqrt examples above).
Sometimes, spaces between parameters makes the program more readable, as in the last call to sum above.
There are also two fundamentally different styles in writing method definitions, e.g.,
For the most part, we will prefer the former.
There are also different styles with regard to the opening brace:
Again, we will prefer the former.

In-Class Exercise 25: Now go back and read through the second two programs for the negative-exponential earlier - see how much easier they are to read with your new found understanding of methods.

When things go wrong

Below, try to identify the errors first by reading, then compile and run to see if you were right.

In-Class Exercise 26: What is wrong with the program below?

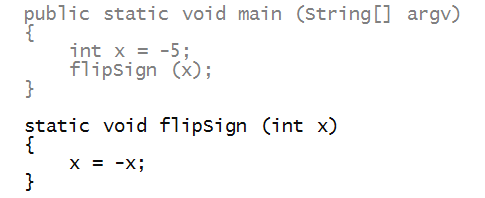
How can you fix it?

In-Class Exercise 27: Identify the errors in the method below:

In-Class Exercise 28: What is the compiler error in the method below?

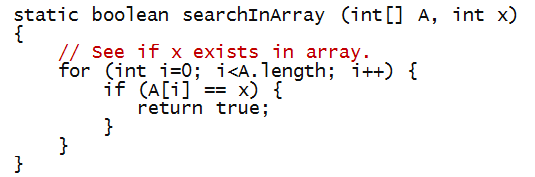
In-Class Exercise 29: Identify the errors in the program below.