Assignment 4

Bonus point opportunity: In this assignment, you can either

Create a simple "OK" algorithm that does reasonably in solving the problem. This algorithm should produce better results than the "naive" algorithm described below (NaiveBoxAlgorithm.java). This is relatively easy to do, as you'll see when you read the problem.
Spend a bit more time and compete to get more points that can then be applied to recover points lost from a previous assignment. Your algorithm will be compared to that of every other solution proposed by students in the course. There will be extra points for devising an algorithm that outperforms the algorithms of most other students. Also, you will be able to create and submit box-problem instances to challenge other students in the class.

You will solve an "unsolved" problem, one that does not have a name yet, even if it's similar to some other problems we've seen. We'll call it the "Box Problem." You will be given a box and a bunch of items with the goal of placing as many items as possible into the box.

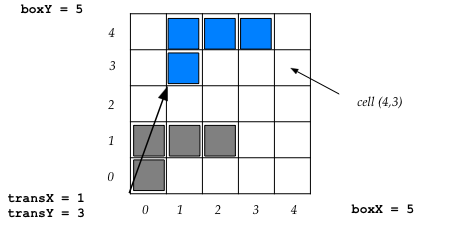
The problem is easily described with a picture:

Here we have a two-dimensional box of width 5 and height 5. (In general, width and height can be different.) This one already has items (six of them numbered 0 to 5, and each with a color) placed in the box, showing a solution. The grid lines are drawn for convenience so that one can view each item as consisting of a group of cells in a fixed geometric pattern (such as the L-shaped item #1), and one can see the whole box as a grid. Item placements need to respect cell boundaries: we can't, for example, place item 0 so that its left edge starts in the middle of a cell.

In a particular instance of the problem, you will be given the box dimensions and the list of items in a plain text file. For instance the above problem is in the text file testproblem2.txt, which looks like this:

5 5
#item 0
 0 0 0 1 1 0 1 1
#item 1
 0 0 0 1 2 2 1 2 0 2
#item 2
 0 0 1 0 2 0 3 0 4 0
#item 3
 1 0 0 3 0 2 0 1 0 0
#item 4
 0 0 0 1 1 1 2 1
#item 5
 1 0 0 0

Let's explain:

The first line has the box width and height (5 by 5).
Lines beginning with a # are comments.
Each item is on a line by itself.
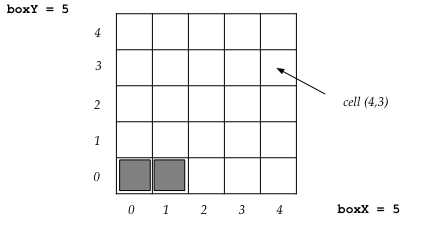
Each item is a collection of contiguous cells that is described as if the item were initially placed near the origin. For example, the last item in the list has two cells: the cell (1,0) and the cell (0,0) - see the picture below.
Fortunately, you don't have to parse the text file. All you need to do is create a problem instance:
```
     BoxProblem problem = new BoxProblem ("testproblem2.txt");
   
```
The class BoxProblem reads and parses the file (assuming the file is in the same directory).

To understand cell coordinates, let's draw the 5x5 grid:

Here, the dimensions are 5x5. You will be able to access this via the public variables problem.boxX, problem.boxY as in:

     BoxProblem problem = new BoxProblem ("testproblem2.txt");
     System.out.println (problem.boxX + " x " + problem.boxY);

To keep the problem simple, we will use an integer grid, where items are groups of contiguous cells.
The item that consists of the two cells (0,0) and (1,0) is shown in the picture above.
Think of a cell's coordinates as the integer coordinates of its bottom left corner.
However, in the solution (first figure), the item is vertical, not horizontal as in the second figure. What gives? The reason is, we are allowed to rotate an item before deciding where to place an item.
Lastly, once an item is rotated (if it's rotated at all), we need to specify where in the box it goes, by specifying a translation.
For example, consider item #4:
In the solution, this item is not rotated but translated by 1 in the x-direction and by 3 in the y-direction.

Your main goal is to write code to solve the problem of deciding which items go into the box, the orientation for each item, and where they are placed (the translation for each item) so that as many items as possible are packed and the as much of the box as possible is used. You will do that by creating a class that implements the BoxProblemAlgorithm interface, which has two methods:

Your method getName() should return your name.
Your method findSolution() should return your solution.

To see an example, take a look at NaiveBoxAlgorithm.java, which implements the interface and features a simple but somewhat ineffective algorithm. To see how it runs, examine the code in TestBoxAlgorithm.java, then compile and run TestBoxAlgorithm.

Start by downloading and unpacking boxproblem.jar. The relevant javadocs:

BoxProblemAlgorithm, the interface.
BoxProblem, which describes a problem.
BoxSolution, which has methods to help you build a solution.
Item, for a particular item.
Cell, for a particular cell.
BoxEvaluation, a class that returns the results of evaluating the solution produced.

Now let's consider some of the details:

First, when writing code for the algorithm, we'll need to understand how to extract the elements of the problem, when given a BoxProblem instance:

The public variables boxX, boxY have the dimensions.

Call getItems() to get all the items in an array-list. Or call getItem() to get a particular item, as in these examples:

     BoxProblem problem = new BoxProblem ("testproblem2.txt");
     // Get all the items:
     ArrayList<Item> items = problem.getItems ();
     // Just the first item:
     Item firstItem = problem.getItem (0);
     // Alternatively:
     firstItem = items.get (0);
     // Examine the item:
     System.out.println (firstItem);

Now let's consider a particular item:
- Each item is an instance of the class Item.
- Each item is identified by a unique ID, which you can read from the public variable ID.
- Since an item is a collection of cells, you can get the whole list of cells by calling getCells().
- Each Cell has x and y values available as public variables: these are the integer coordinates of the cell's lower left corner.
- The Item class also has useful methods to rotate an item anti-clockwise by 90 degrees, or to rotate an item to a given orientation. Similarly, you can translate an item by a given (x,y) amount.
- Both Item and Cell have toString() methods for debugging.
The orientation of an item is the amount the item needs to be rotated before placement in the box. There are only four possible orientations:
1. The default is orientation=0.
2. When orientation=1, the item is rotated anti-clockwise by 90 degrees.
3. When orientation=2, the item is rotated anti-clockwise by 180 degrees.
4. When orientation=3, the item is rotated anti-clockwise by 270 degrees.
When you place items, it's up to you to decide the orientation so that you can take advantage of rotations to more cleverly fit as many items as possible.
When placing an item, you will also need to provide its translation. The default is no translation, which means the item will touch the x and y axes. Clearly, it's very likely that two un-translated items will overlap, which is not allowed. Thus, except possibly for one item, all items will need some translation.
To place an item in the box, once you've decided its orientation and translation, call the put() method of the solution instance. For example, consider:
```
        BoxSolution solution = new BoxSolution ();
        solution.put (0, 0, 0, 0);
        solution.put (1, 0, 0, 1);
        solution.put (2, 1, 0, 2);   
   
```
This places items 0, 1, 2 in sequence (first parameter). The second parameter is the orientation and the third and fourth are the translation amounts to determine where to place the item in the box. Thus, above, the 3rd item (item with ID=2) is translated along the y-direction by 2 units, with an orientation that rotates it by 90 degrees anti-clockwise. See the examples in BoxProblemExamples.java, that's included in the jar.
Testing your code:
- Edit the file TestBoxAlgorithm to replace NaiveBoxAlgorithm with your class.
- Notice that you can test with a single problem instance and view your solution, or you can test across multiple problems and obtain an "average-across-the-problems" performance report.
- The jar file contains three test problems, in the files testproblem1.txt, testproblem2.txt, testproblem2.txt, of increasing difficulty.

This should be enough to get started. However, there are some additional tools that you may find useful:

Since the text file that describes a problem is hard to visualize, you can view a problem by browsing through the items in a problem, for example:
```
    java ItemBrowser testproblem2.txt
    
```
Similarly, it helps to see your solution. You can do this programmatically by seeing the example in TestBoxAlgorithm, which calls SolutionViewer.
Finally, you are encouraged to submit a 10x10 or 20x20 problem that's "hard" as a challenge problem for others but one that your algorithm solves. That is, your algorithms fits all the items but others will find it hard to fit all items into the box. To create such a problem, use
```
    java BoxProblemDesigner 10 10
    
```
which sets you up with a 10x10 grid and a simple interface in which to draw items by clicking on cells. Your goal is to create a problem instance for which your algorithm is able to pack all items in the box, but which others would find hard. But to have your problem qualify, your algorithm will need to solve other problems well too. That is, you can't code up an algorithm that's explicitly tied to your particular problem.

The competition:

We will run each student's algorithm on the problems currently included, and on a few additional problems we will create, and on select problem instances that you submit.
We will examine both the number of items packed and the average area (number of cells) packed.
Some points will be awarded for placing well in the competition.

Submission:

Name your file with your username as part of the file name. For examplem if your username is xyz, call your file XyzBoxAlgorithm.
Name your problem submission similarly, for example Xyzproblem.txt.
IMPORTANT: write all your code in that one file. You can of course use multiple methods, and create your own classes, but please put all the code in one file. The reason is, we will have all student code in one directory: it will be convenient with fewer files.
You'll need to follow the usual submission instructions carefully.
The name of subdirectory should be: your username followed by _a4.
Example: if your username is xyz your subdirectory will be called xyz_a4.
Thus, the jar file will be called xyz_a4.jar.