Assignment 3

  1. PART I: Pen-and-paper exercises:

    1. Review dynamic programming in Module 9 and work through Module exercise 9.10 as part of the Assignment 3 submission.

    2. Module exercise 10.12.

    3. Submit a detailed response to Module exercise 11.5, especially showing the bin-packing transformation when we use the metric of "minimize the largest weight carried by any individual".

    4. Read about Turing Award winners Steven Cook and Richard Karp. What were their contributions to the theory of algorithms? Write a few sentences to explain at a high level and distinguish their contributions.
    Note: Credit will not be given only for answers - show all your work: your reasoning, steps you took to get your answer etc.

  2. PART II: Implementation: In this part, you will implement two algorithms for a version of the graph partitioning problem.

    Let's first formally define the problem:

    • The input is a weighted graph (i.e., the edges have weights).
    • Let V be the set of vertices and E the set of edges.
    • The output is a partition of the vertices into two equal-size sets. Let's call these sets Set1 and Set2. Each vertex either belongs to Set1 or to Set2 (but not both). For an n vertex graph, each set should have about n/2 elements (depending on whether n is odd or even).
    • What if there are an odd number of vertices? Then, pick Set1 so that its size is one less than Set2.
    • Note: since Set2 = V - Set1, all we have to do is specify Set1.
    • The "cost" of a partition is computed as follows. Let F be the set of edges that go between partitions, i.e., all those edges that have one vertex in Set1 and one in Set2. Now total up the edge weights of the edges in F. This is the "cost" of the partition.
    • The goal: find a partition with minimal cost.
    • For example, consider this 4-node graph:

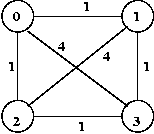
      • For the partition Set1={0,1}, there are four partition edges with total cost 4+4+1+1 = 10.
      • Similarly, for the partition Set1={0,2}, there are four partition edges with total cost 4+4+1+1 = 10.
      • However, for partition Set1={0,3}, the total cost is 1+1+1+1 = 4. This turns out to be the optimal partition.
    • Note: the vertices in Set1 need not themselves form a connected graph. Likewise for the vertices in Set2.

    You will implement two algorithms:

    • A "greedy" algorithm that should execute in polynomial time.
      Note: implement a "greedy constructive algorithm" (that builds a solution step by step) as opposed to a "greedy-local-search" algorithm (that jumps around neighborhoods in the state space).
    • Simulated annealing.

    Implementation details:

    • Call your classes Greedy and Annealing.
    • Both classes will need to implement the GraphPartitioningAlgorithm interface.
    • The interface has only one method: 
          int[] findPartition (double[][] adjMatrix)
      Here, the input is a weighted graph represented by an adjacency matrix. A value of zero in the matrix indicates lack of an edge; otherwise the entry is the weight of the edge. The return value is the set of vertices in Set1 (the first partition). Thus, if the method call is made as follows: 
          int[] set1 = findPartition (adjMatrix);
      then set1.length is the number of vertices in Set1 and set1[i] is the i-th vertex in the set. Thus, in the optimal solution for the example above, we should expect set1[0]=0, set1[1]=3.
    • Use the following properties file to run your algorithm in the test environment.
    • Note that the test environment does not do much correctness-testing. The nature of optimization problems is that any dumb algorithm can produce a valid assignment - the value comes from the quality of the assignment. Thus, you need to submit evidence that your non-naive algorithms are doing "some good". Compare the quality of solution produced and time taken to produce the solutions for these algorithms.
    • Submit an example (on paper) to show that your greedy algorithm does not always produce the optimal solution.
    • Analyse the running time (in order-notation, on paper) of your greedy algorithm.
    • Using an example (on paper), explain the neighborhood function used by your implementation of simulated annealing.
    • You will need to download the latest version of the test environment.

  3. [Optional: for recovery points] As part of Assignment 3, you can re-do the programming parts of either one of Assignment 1 or Assignment 2 and get back some lost points for one of those submissions:
    • Use the same submission place in BB for Assignment 1 if submitting that.
    • Make a clear note in your Assignment 3 PDF that you are re-submitting, and explaining which assignment, and what exactly has been fixed.
    • Generally, we will expect the updated version to run near perfectly, and that the submission will occur by the posted Assignment 3 deadline. That is, if you wish to avail of this opportunity to recover points, then no extension will apply either to Assignment 3 or this optional resubmission to an earlier submission.
    • You will not be able to get back all lost points, only a modest and reasonable fraction. Nor can we specify now how the resubmission will be scored.

Submission: