Assignment 2

  1. PART I: Pen-and-paper exercises:
    1. Analyze the following code and provide a "Big-Oh" estimate of its running time in terms of n. Explain your analysis. 
      
    s = 0;
    i = 1;
    while (s < n) {
      s = s + i;
      i = i + 1;
    }
    2. Simplify O (n * (n2 + log(n) * (3*n + (3*n2)/log(n) ) ) ).
    3. Explain (with a detailed argument) that a full trie with O(n) leaves has at most O(n) interior nodes.
    4. Consider the following high-level pseudocode for a recursive text search algorithm given the text and pattern. 
      
   Algorithm: textSearch (text, pattern)
   Input: two char arrays text and pattern of lengths n and m
   1.    for i=0 to n-1
   2.       if recursiveMatch (i, 0, m-1)
   3.           return true
   4.       endif
   5.    endfor
   6.    return false

   Algorithm: recursiveMatch (i, p, q)
   Input: See if there's a match at position i in text with 
          the chars in the pattern between positions p and q
   1.   // Base cases ... not shown

        // Find the middle index.
   2.   m = (p+q)/2
   3.   If both the left half and right half of the range [p,q] match, 
        then return true otherwise return false
      Flesh out the pseudocode with details (base cases, and the recursive calls. Then, analyze the algorithm's execution time: what is the worst-case execution time in terms of m and n?
    5. Who is the "K" in the KMP text search algorithm we studied? Describe three of his contributions to computer science.
    Note: Credit will not be given only for answers - show all your work: your reasoning, steps you took to get your answer etc.

  2. PART I: Implementation: In this part, you will implement the naive algorithm for the rectangle-set intersection problem. In this problem the input consists of two sets of rectangles. The goal is to identify all pairs of rectangles that intersect where the first rectangle in each pair is from the first set, and the other rectangle in the pair is from the second set.

    Rectangles can be specified in many ways. We will use the following convention: the top-left and bottom-right corners. If you know these two points, then the two points uniquely determine a rectangle.

    For example, consider these two sets of rectangles in the region specified by (0,100) and (100,0):

    • Set1 = {R1, R2, R3} where
      R1 = [ (5,80), (20,70) ]
      R2 = [ (20,60), (40,50) ]
      R3 = [ (20,30), (40,20) ]
    • Set2 = {R4, R5, R6, R7} where
      R4 = [ (70,80), (80,70) ]
      R5 = [ (30.55), (60.25) ]
      R6 = [ (50,30), (65,20) ]
      R7 = [ (70,30), (80,20) ]
    You can see that R2 intersects R5, and R3 intersects R5. These are the intersections to report: R2-R5 and R3-R5. It so happens that R5 and R6 intersect, but since they are from the same set, we don't report this intersection. The naive algorithm works by examining each possible pair of rectangles (one from each set) and determining whether the pair intersect, similar to the naive algorithm for the largest-distance problem in Module 1.

    Now, determining whether two rectangles intersect requires some clarification:

    • To simplify the problem, we will use only integer coordinates. That is, the corners of rectangles, as well as the boundaries of the region will be specified with integer coordinates.
    • We will consider two rectangles as intersecting if they have any point in commong, even a single point (a corner) in common. Thus, R1=[(1,5), (5,1)] and R2=[(5,10), (10,5)] intersect even though (5,5) is the only point they have in common. Similarly two rectangles are considered intersecting if any of their sides overlap a bit, one is inside the other or exactly overlap. Thus, if you think of a rectangle as the set of points on its boundary and in its interior, then two rectangles intersect if their point-sets have a point (or more) in common.

    To implement:

    • Write your code in a class called NaiveRectIntersection.java. This class will need to implement the RectangleSetIntersectionAlgorithm interface.
    • The classes/interfaces involved are:
      • Algorithm. The interface for all algorithms that use the test-environment.
      • RectangleSetIntersectionAlgorithm. This is the interface for algorithms that solve the rectangle-set-intersection problem.
      • IntPoint. A class that represents a point with x and y values (as int's).
      • IntRectangle. A class that represents a rectangle with integer coordinates.
      • IntPair. A class that represents a pair of rectangle ID's (as int's).
      Note that IntPoint, IntRectangle and IntPair are already implemented for you; you will merely use these classes.
    • Note: each rectangle instance will have a unique ID. Thus, the input sets consist of two arrays of rectangles, each of which will have a unique ID. Suppose a rectangle with ID=5 is in the first set and that it intersects with a rectangle with ID=12 in the second set. Then, you will need to return the pair (5,12) as part of the return value of the method in RectangleSetIntersectionAlgorithm. How do you create the pair? Simply create an instance of IntPair as in: 
      
     IntPair ip = new IntPair (5, 12);
      Of course, you will be doing this in a loop and will be creating instances to add to the array that you will finally return in the method findIntersections.
    • Important: if there are no intersections, you should return null.
    • You will need the following import statements in your classes: 
      
import edu.gwu.algtest.*;
import edu.gwu.util.*;
import edu.gwu.geometry.*;
import java.util.*;
    • You may use the following properties file to test.

  3. PART I: Pseudocode: Read through part II below and provide pseudocode for your algorithm(s). Since part II is not trivial, this will get you started with thinking about part II. Write your pseudocode neatly using the style in the modules. Note: we will grade your pseudocode and compare it with your actual code the following week. So, you really need to think about your pseudocode carefully and plan on using it for Part II.

  4. PART II Implementation: In this part, you will implement an interesting tree-like structure to reduce the number of rectangle-intersections computed.

    Here's how it would work:

    • The tree structure is called a Rectangle Filter Tree.
    • For starters, let us consider a data set consisting of a collection of rectangles and show how a data set of rectangles is inserted into a filter tree (just as a data set of strings might be inserted into a binary search tree). Later, we will show how to relate this structure to our original problem of finding intersections amongst rectangles in two data sets.
    • The general idea is to break up the region into imaginary sub-rectangles, that are each then subdivided into imaginary (and smaller) sub-rectangles ... and so on. We take our input set of data rectangles and insert each rectangle one by one into the filter tree. The data rectangles are usually quite small and will get inserted into the appropriate sub-rectangle in the tree. Hopefully, if the data rectangles are spread out, then they'll spread out over the tree, allowing for efficient search later on.
    • A picture will help us understand the details. Let's consider inserting the following five data rectangles into a filter tree that spans the region defined by [(0,100), (100,0)]:
      R1 = [(89,57), (91,37)]
      R2 = [(12,80), (45,66)]
      R3 = [(28,40), (39,29)]
      R4 = [(18,70), (32,60)]
      R5 = [(79,94), (82,90)]

      Here are the rectangles depicted in the region [(0,100), (100,0)]:

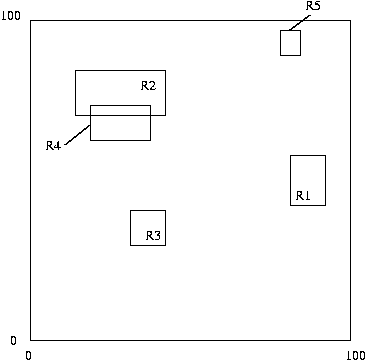
    • First, we will look at what the filter tree looks like after all five data rectangles are inserted. Staring at this might be enough to understand how it works. We'll go through the steps next.

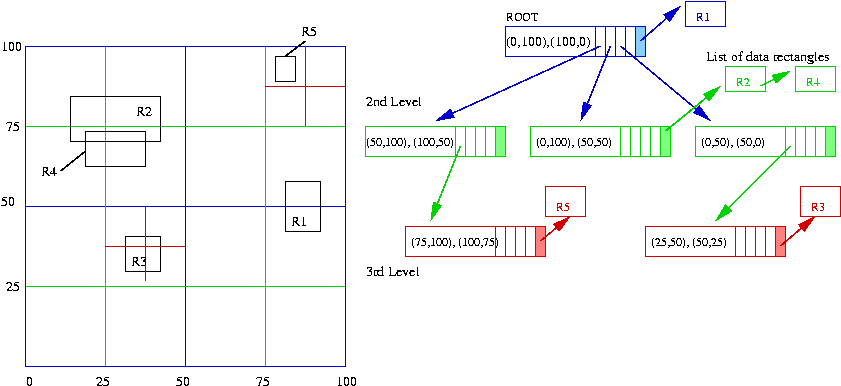
    • Here's an intuitive way to understand filter trees and to see why it's so named. The enclosing region [(0,100), (100,0)] represents the root node of the tree. Now the root node has horizontal and vertical bisectors. The horizontal bisector is the line that cuts the rectangle in half horizontally; the vertical bisector cuts the rectangle in half in the vertical direction.
      Note that the bisectors together create four smaller sub-rectangles that we will call quadrants (squares, in this particular example). These four sub-rectangles form the four nodes at the next level of the filter tree. Each of these can be bisected horizontally and vertically to form 16 nodes at the third level of the tree ... and so on.
      Now suppose we built a wire-frame grid for each rectangle at each level and "dropped" the data rectangles from above. Some data rectangles would fall through the top level (R2, R3, R4, R5), while others (R1) would get "trapped". The level at which a data rectangle gets trapped determines the node in the tree where the data rectangle gets stored. Of course, we limit the number of levels so that eventually a data rectangle gets stored somewhere.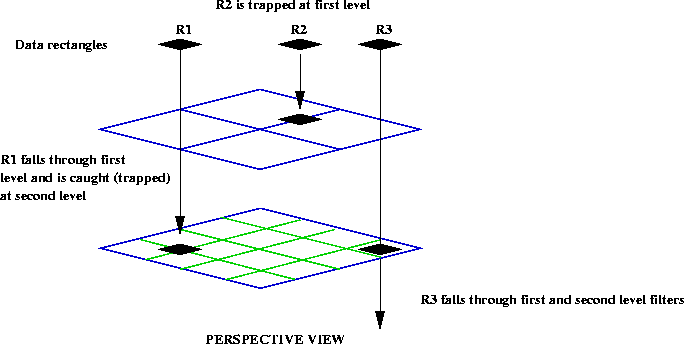

    • Now let's examine how the five data rectangles got inserted one by one.
      • In our example, we will build a 3-level tree (Filter trees can have arbitrary depth).
      • Initially, the root node is empty and there are no data rectangles:

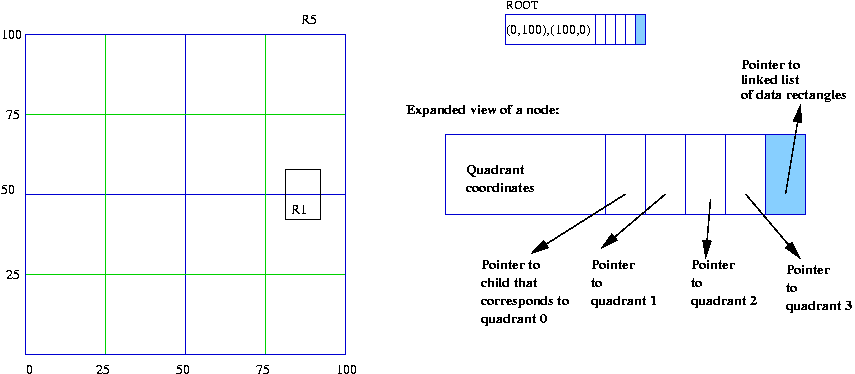
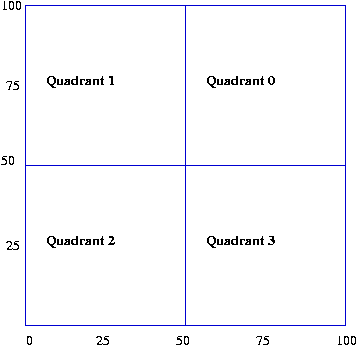
      • We will use this convention for numbering the quadrants: quadrant 0 is the Northeast quadrant, quadrant 1 is the Northwest quadrant ... and so on.

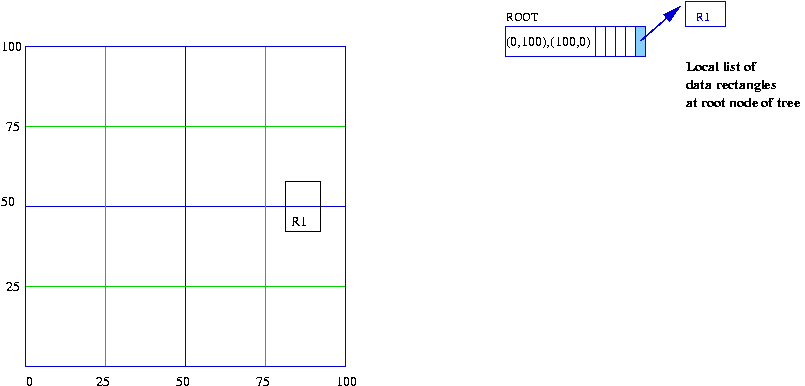
      • The first data rectangle (R1 = [(89,57), (91,37)]) is "dropped" into the current tree. It happens to get trapped at the root level and is stored in a linked list off of the root level.

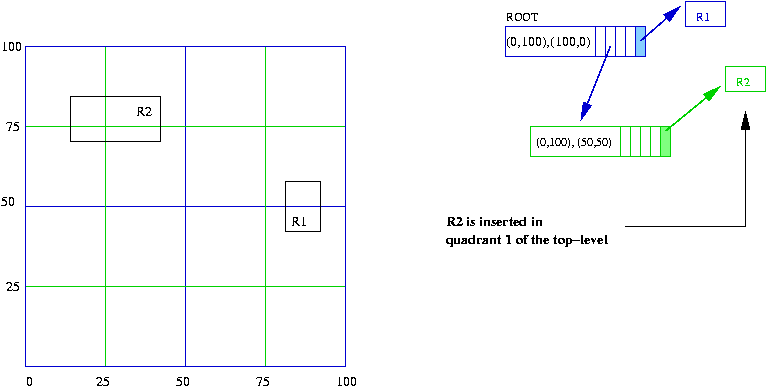
      • The second data rectangle (R2 = [(12,80), (45,66)]) is now dropped into the tree. It falls through the root into quadrant 1. However, no node exists in the tree for quadrant 1, so we create it. R2 gets trapped by the bisectors of this sub-rectangle so it gets stored in the linked list off of this tree node.

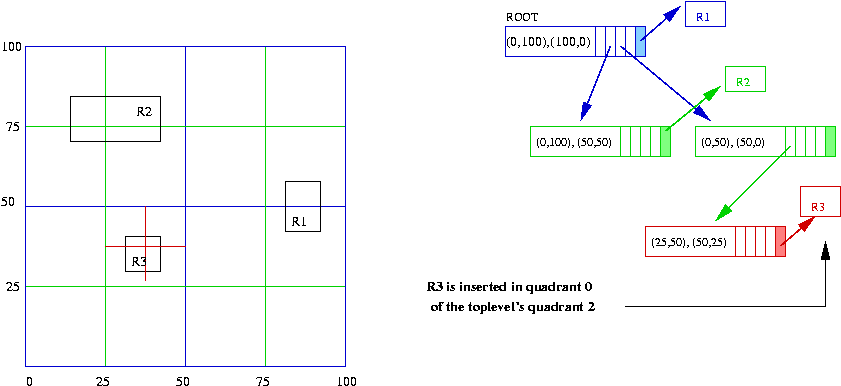
      • The third data rectangle (R3 = [(28,40), (39,29)]) is now dropped into the current tree. It falls through the root node, into quadrant 2, which needs to be created. Once it's created, R3 also falls through the second-level node into the third level, where it gets trapped:

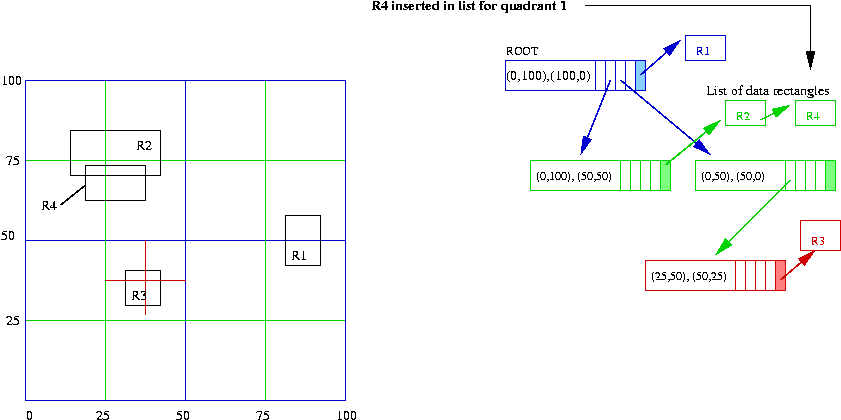
      • The fourth data rectangle (R4 = [(18,70), (32,60)]) falls through the root and gets trapped at the next level in the rectangle for quadrant 1 (of the root). This is where it gets stored:

      • The fifth data rectangle (R5 = [(79,94), (82,90)]) falls through the root (quadrant 0, which is created), then falls through quadrant 0 of the second level (which is created at the third level of the tree). It also falls through the third level, but since we are limiting the number of levels to three, we store the rectangle at this level.

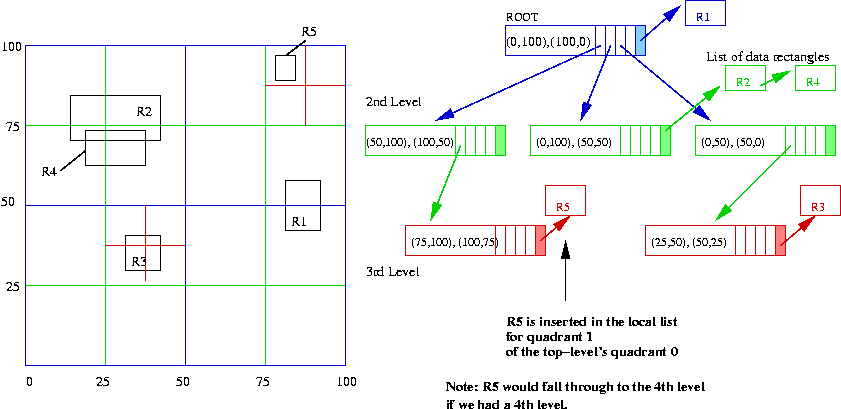
      • The tree is now constructed.
      • The most important observation to make is that each sub-rectangle in the tree is treated in the same way. Thus, it is easy to write recursive code for insertion.

    • Next, consider how searching is done in the tree:
      • What does "search" really mean in this geometric-object context?
        => In search, the input is a "query" rectangle Q for which we need to find all the data rectangles that intersect with Q.
      • Consider the example Q = [(20,64), (36,38)]. Simply eyeballing the data tells you that Q intersects R3 and R4. But how do we automate searching in the tree?
      • The idea is to perform search similar to insertion. Start by checking whether Q intersects any data rectangle stored off of the root node. Then, compute which quadrants Q intersects with. Then recursively search each of these quadrants.
    • Finally, let's consider how a filter tree can be used for the two-set intersection problem. Recall that the input to this problem consists of two sets of rectangles. First, insert one set of data rectangles into a filter tree. Then, use each rectangle in the second set to query against the tree. 
      
  Algorithm: findIntersections (rectSet1, rectSet2)
  Input: two sets of rectangles containing n and m rectangles respectively
       // First, place data rectangles in rectSet1 into tree.
  1.   makeFilterTree (rectSet1)
       // Now scan rectangles in second set and query against tree.
  2    for i = 0 to m
         // Get list of intersections from tree.
  3.     LinkedList intersectionSet = filterTreeSearch (rectSet2[i]);
  4.     if intersectionSet not empty
  5.       numIntersections += intersectionSet.size();
  6.       Place intersections in intersectionSet into list of intersections;
  7.     endif
  8.   endfor
  9.   return all intersections;
    Implementation:
    • Name your algorithm FilterTreeRectIntersection.java.
    • Your algorithm will need to implement the RectangleSetIntersectionAlgorithm interface that itself extends the Algorithm interface you've already used. Also see the other javadocs referenced above.
    • Use instances of the class FilterTreeNode for each tree node. Note that the constructor of this class computes the vertical and horizontal bisectors.
    • Note about the region size:
      • You can identify the region size by scanning all data rectangles and recording the min and max of the X and Y values.
      • However, for the basic test case of showing the same results as in the picture above, you'll need to (just for this test case) use the 100 x 100 region.
    • Suggested steps for implementation:
      • Start with some pen-and-paper work: write down detailed pseudocode for insertion and search in the filter tree, and for the two-set intersection that uses the tree. Submit this pseudocode in Part I.
      • You will find it useful to write code that decides whether two given rectangles intersect. Likewise, you will find it useful to write code to identify whether a given rectangle intersects with a node's bisectors.
      • First get your code working for just two rectangles in each rectangle set.
    • Implement a print-tree method. Use the 5-rectangle example above to show that your code is working correctly. Submit PDF output from your print-tree with this example, and another example.
    • Compare the performance of the filter tree approach with the naive method. Do not spew out debugging into or print-tree output for this part.
    • You may use this properties file with the test environment.
    • Try filter trees of different depths, and adjust the region and rectangle sizes to see when the filter tree performs well.
    • Submit your pseudocode as part of your Part II submission as well.

Submission: