Assignment 1

  1. PART I: Pen-and-paper
    1. Analyze the following code and provide a "Big-Oh" estimate of its running time in terms of n. Explain your analysis. 
      
    void compute (int n, double[][] A, double[][] B, double[][] C, double[][] D)
    {
       for (int i=0; i < n; i++) {
         for (int j=0; j < n; j++) {
           C[i][j] = A[i][j] + B[i][j];
         }
       }

       for (int i=0; i < n; i++) {
         for (int j=0; j < n; j++) {
           for (int k=0; k < n; k++)
              D[i][j] = D[i][j] + A[i][k] * B[k][j];
         }
       }

    }
    2. Module (in-class) exercise 2.9. Repeat that here, in full detail. This is a way to highlight the importance of certain module exercises and to get additional points for the same work.
    3. Consider the following example of a binary tree:

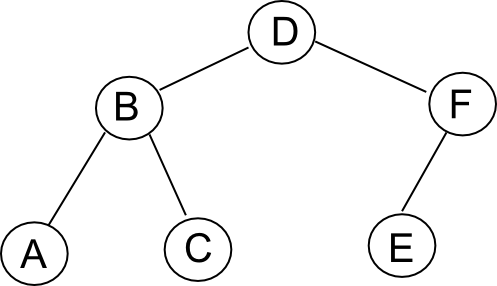      There are several different ways of printing the nodes in a binary tree:

      • Define a level-print as the sequence of nodes you get when you start at the top and go level by level, and going left to right. With the tree above, you get: "D B F A C E".
      • Define a Node-Left-Right-print (NLR-print, for short) recursively as follows: print the node, then recursively print the left subtree, then recursively print the right subtree. With the tree above, you get: "D B A C F E".
      • Define a Left-Right-Node-print (LRN-print, for short) recursively as follows: recursively print the left subtree, then recursively print the right subtree, then print the node. With the tree above, you get: "A C B E F D".
      Write neat, detailed pseudocode for each of the three print methods, making sure you handle the bottom-out cases for the recursion. Trace the execution of the three print methods using the above example, showing the contents of the stack at each step.
    4. Who is generally credited with the invention or discovery of MergeSort? Write a few sentences summarizing this person's contributions to computing.

  2. PART II: Pen-and-paper
    • Insert the nine (1-letter) keys "A B C D E F G H I" into an empty multiway tree of degree 2 and show the intermediate steps. Also, work out the insertion steps for a multiway tree of degree 3.
    • Show the intermediate trees when the seven keys "D A C B E F G" get inserted into a self-adjusting binary tree. Remember that a newly inserted element is moved to the root so that every insertion will cause re-organization. Write down the which rotation case (e.g., Case 1(a), Case 3, etc) you are using with each diagram.

  3. PART II: Implement (1) a binary search tree, and (2) a self-adjusting binary tree as described in Module 3. In particular:
    • Your algorithms will need to implement the TreeSearchAlgorithm interface that itself extends the OrderedSearchAlgorithm interface. The only addition with the second interface is, you will make the root of your tree available public (for testing).
    • To understand how enumeration works for a data structure, read through this Enumeration example.
    • Recall that deletion for a self-adjusting tree is the same as in a regular binary search tree. Most importantly, both insertion and search in a self-adjusting binary tree cause the node in question to be moved into the root position.
    • Make sure that your follow the five CASES described in Module 3 and that you indicate in comments which sections of code apply to which case.
    • Note that you will be building your tree code using the TreeNode class. In this class, all you will need to use are the three fields left, right and parent. You may choose to use a constructor if you wish but do not have to since all these variables are public.
    • Make sure that your code properly sets the parent field for each tree node.
    • As usual, you will need to include tests in your main method. In particular, include the example from Part I above.
    • Write your binary search tree code in a file called BinarySearchTree and your self adjusting tree in SelfAdjTree.java.
    • Suggested steps for implementation:
      • First, implement search and insertion for the simple binary search tree. This will get you comfortable with "tree" programming. Try to do this in the first week. Also, use the pseudocode towards the end of Module3 (for self-adjusting trees) as a starting point - just comment out the part about moving a newly-inserted (or searched-for) element to the root.
      • Then, implement deletion for binary search trees and test.
      • Next, use the binary search tree code as the starting point for your self-adjusting tree. Implement the splaysteps, and try it out only on search. (This way, you avoid having to debug both insertion and moving-to-root at the same time).
      • Finally, implement insertion and the rest of the operations.
    • Note: the test environment will throw several tests at your implementation. For each test, the test-environment will call your tree's initialize() method where you will have a chance to reset, set the root to null etc.
    • Your tree should not need to know the data types of the keys and values, that is, whether they are strings or integers or something else. All that's needed is that keys need to be Comparable. The values can be of any object type. The test-environment will indeed provide such keys and objects.
    • Compare the performance of the self-adjusting tree with the binary search tree.
    • You may use this properties file. Initially, to make testing and development a little easy, set "testDelete=false", "testLarge=false", "testPredSucc=false", and "testEnum=false". This will make sure that deletion, large-size data, and enumeration do not get tested. Later, when you have insertion and search working, you can set these to true. Leave "equalitySearch=false".
    • Before starting, download the latest version of the test environment (algtest.jar). This is a good thing to do for each assignment, just in case there have been changes made to the test-environment code.
    • Relevant links:
      Algorithm interface
      SearchAlgorithm interface
      OrderedSearchAlgorithm interface
      TreeSearchAlgorithm interface
      TreeNode class
      ComparableKeyValuePair class
    • NOTE: Do NOT write source code for these interfaces, nor for classes like TreeNode. They are all already in algtest.jar. If you write them, you'll be able to compile but will get a class-cast error.

Submission: