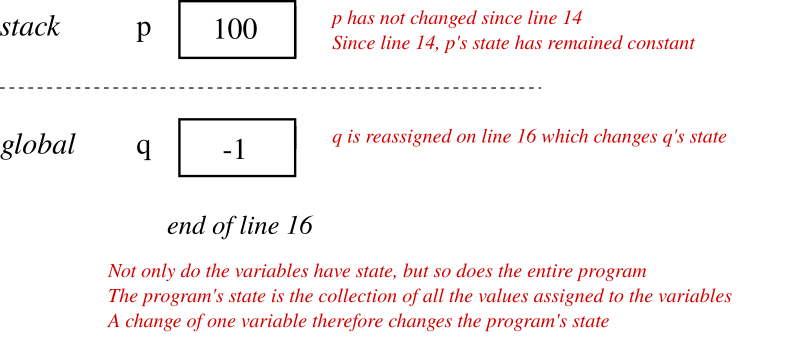Module 1: Unidimensional Arrays
Supplemental material
Arrays of integers
Let's start with a simple example:
public class OddNumbers {
public static void main (String[] argv)
{
// Declare an array variable (to hold int's) and initialize
// it with values.
int[] oddIntegers = {1, 3, 5, 7, 9};
// Print some attributes of the array.
System.out.println ("Array length: " + oddIntegers.length);
System.out.println ("First index=0, last index=" + (oddIntegers.length-1));
// Next, the elements along one line.
System.out.print ("Array elements: ");
for (int i=0; i < oddIntegers.length; i++) {
// Note: "print" and not "println"
System.out.print (" " + oddIntegers[i]);
}
System.out.println ();
}
}
Note:
- Arrays can be populated using hard-coded constants:
int[] oddIntegers = {1, 3, 5, 7, 9};
- In this case, assignment may not follow declaration:
int[] oddIntegers;
oddIntegers = {1, 3, 5, 7, 9}; // Won't compile.
- Assignment can follow declaration in other cases:
// Pure declaration.
int[] oddIntegers;
// Create space.
oddIntegers = new int [5];
// Assign values to individual locations.
oddIntegers[0] = 1;
oddIntegers[1] = 3;
oddIntegers[2] = 5;
oddIntegers[3] = 7;
oddIntegers[4] = 9;
Let's look at a little variation:
// We need this for the class java.util.Arrays.
import java.util.*;
public class OddNumbers2 {
public static void main (String[] argv)
{
// Declare and create space at once.
int[] oddIntegers = new int [5];
for (int i=0; i < oddIntegers.length; i++) {
oddIntegers[i] = 2*i + 1;
}
// The class Arrays has many useful methods, among which is:
String outputStr = Arrays.toString (oddIntegers);
System.out.println (outputStr);
}
}
And another variation:
import java.util.*;
public class OddNumbers3 {
public static void main (String[] argv)
{
// If we want to make various such arrays, it makes sense
// to put this in a method.
int[] oddIntegers = makeOddArray (5);
System.out.println ( "Our array: " + Arrays.toString(oddIntegers) );
}
// Note: return type is an array.
static int[] makeOddArray (int size)
{
// Note use of variable "size" in creating array space.
int[] oddGuys = new int [size];
for (int i=0; i < oddGuys.length; i++) {
oddGuys[i] = 2*i + 1;
}
return oddGuys;
}
}
In-Class Exercise 1:
Download OddExercise.java and
implement the method search() to search in an array
of integers.
Character arrays
Consider this example:
import java.util.*;
public class CharExample {
public static void main (String[] argv)
{
// Make a character array and initialize it.
char[] letters = {'f', 'a', 'c', 'e', 't', 'i', 'o', 'u', 's'};
System.out.println ( Arrays.toString(letters) + " has " + letters.length + " chars");
// Make a char array via a String.
String s = "facetious";
char[] letters2 = s.toCharArray ();
System.out.println ( Arrays.toString(letters2) + " has " + letters2.length + " chars");
// Directly create and assign each element.
char[] letters3 = new char [4];
letters3[0] = 'f';
letters3[1] = 'a';
letters3[2] = 'c';
letters3[3] = 'e';
System.out.println ( Arrays.toString(letters3) + " has " + letters3.length + " chars");
}
}
Thus, char arrays are not very different from
int arrays.
In-Class Exercise 2:
Download CharExercise.java and
implement the method checkEqual() to see if two
char arrays are exactly the same.
How stuff is stored: a first look at memory
Let's start with a high-level conceptual view of memory:
- By memory, we mean a computer's main memory
as opposed to hard disk or removable media like CD's.
- Physically, memory is housed inside a chip like this:

- You can think of a memory chip as box with the following
functions:
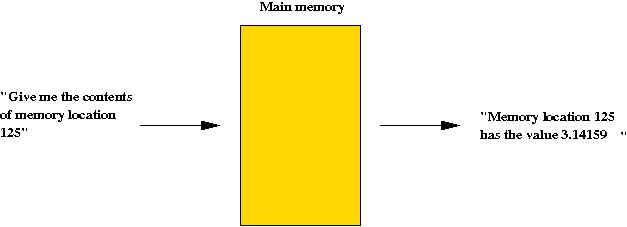
- Reading: You give it a memory address; it gives you
the contents of that memory address:
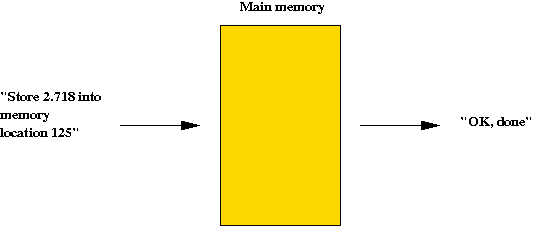
- Writing: You give it a memory-address and a value, and
it stores the value in that location.
- You can think of memory as operating like a hotel reception
with mailboxes:

- When you want to get (read) something: you provide your
mailbox number (memory-address) and the concierge gives you the contents.
- When you want to put (store) something: you provide the
contents and the mailbox number (address), and the
concierge stuffs it in.
- Conceptually, it helps to think of memory as a long
collection of numbered locations:

There is another conceptual view that's useful:
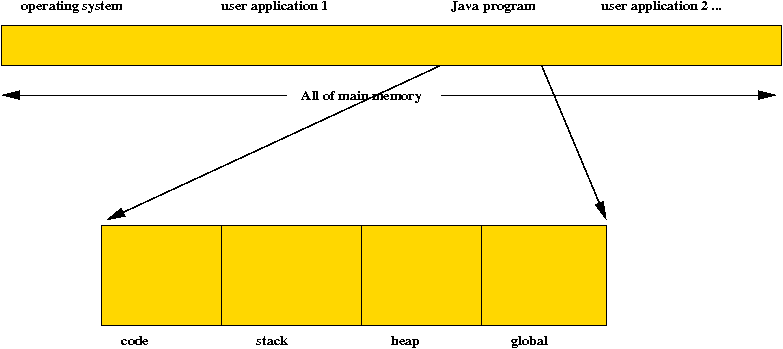
- First, let's step back and look at all of memory as one block:

- Within this, parts are allocated to the operating system and to
a user's applications.
- The user's Java program is one such application.
- The space allocated to the Java program itself has parts:
place for the code, and for three types of program memory:
- The stack: where local variables and parameters are
stored.
- The heap: where arrays and objects are stored.
- The global area: where everything else (like static
variables) is stored.
Now consider a simple program:
public class Simple {
static int a;
static int b;
static int c;
public static void main (String[] argv)
{
// At this point: a==0, b==0, c==0;
a = 5;
// At this point: a==5, b==0, c==0;
b = 1;
// At this point: a==5, b==1, c==0;
c = a + b;
// At this point: a==5, b==1, c==6;
}
}
Note:
- Initially, space is allocated (in the "global area") for the variables:
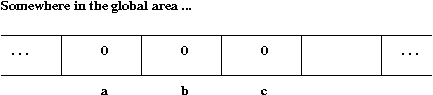
- Then, after the first assignment:

- After the last assignment:

Next, let's consider arrays:
public class Simple2 {
static int a;
static int b;
static int c;
static int[] A;
public static void main (String[] argv)
{
// At this point: a==0, b==0, c==0, A==null;
a = 5;
// At this point: a==5, b==0, c==0, A==null;
b = 1;
// At this point: a==5, b==1, c==0, A==null;
c = a + b;
// At this point: a==5, b==1, c==6, A==null;
A = new int [4];
// At this point: A will have an address (a pointer).
}
}
Note:
- In some languages, space for arrays is allocated in the global
area:

- In Java:
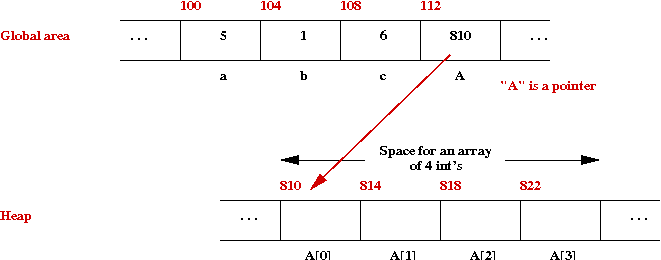
- The variable A is itself in the global area (at
address 112).
- The variable A contains the address ("810") of the actual
array.
- The actual array with its contents is allocated on the
heap at address "810".
- What happens with assignment? Consider this modification:
public class Simple3 {
static int a;
static int b;
static int c;
static int[] A;
public static void main (String[] argv)
{
// At this point: a==0, b==0, c==0, A==null;
a = 5;
// At this point: a==5, b==0, c==0, A==null;
b = 1;
// At this point: a==5, b==1, c==0, A==null;
c = a + b;
// At this point: a==5, b==1, c==6, A==null;
A = new int [4];
// At this point: A will have an address (a pointer).
A[2] = 12;
// At this point: A[0]==0, A[1]==0, A[2]==12, A[3]==0.
}
}
- Initially, when allocated, the array contents will be all zero.
- After the assignment A[2] = 12:
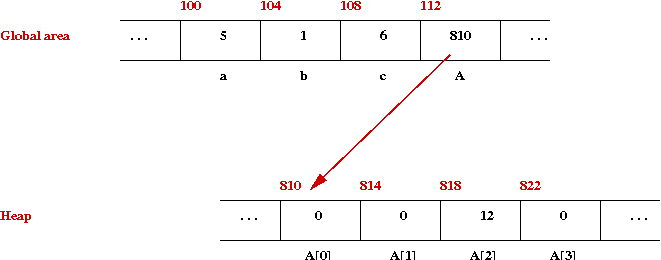
Let's summarize what we've learned:
- Main memory is a sequence of locations, each of which
has a numeric address (like "812" above).
- At the highest level, various parts of memory are allocated
to programs like the operating system and applications.
- Your Java program runs as one application.
- The memory allocated to your program itself has four parts:
code, stack, heap, global.
- static variables are allocated in the global area.
- An array is a contiguous sequence of memory locations.
- Array variables are really pointers: an array
variable points to an area of heap memory where the actual
contents are.
- The term "pointer" is used in the sense that an envelope
with your address on it "points" to you: it has information on
how to reach you (your address).
The idea of a memory pointer is a really important one
that we will encounter many times in this course.
In-Class Exercise 3:
Why are the addresses above numbered 100, 104, 108, ... , instead
of 100, 101, 102, ... ?
To answer this question, Consider the following...
- Computers use binary representation meaning that computers can only represent values as either a 0 or 1. The smallest indivisible binary data unit is called a "bit".
- To represent more than just two values, we group together a number of bits into larger data units. We typically call 8 contiguous bits a "byte". 1 byte (8 bits) can represent a maximum number of 256 discrete values.
- Computer architects group together several bytes to form data units that can represent more than 256 values. When a computer architecture is described as 32-bit or 64-bit, this generally describes the number of bits grouped together to form an address.
- If there are 8 bits to a byte, then a 32-bit value is also a 4-byte value. In a 32-bit architecture, an int is a 4-byte data unit, so whenever an int is declared, it requires 4 bytes of to address the entire int.
- If the array in the example above was declared instead as a byte array instead, each data unit would only require 1 byte.
- This is primarily provided for context as this topic is one of the central topics of your future Computer Architecture class.
In case you were wondering what kinds of variables are
allocated on the heap or stack, here's
a preview:
class MySpecialObject {
// Space for this variable is allocated on the heap.
int a;
}
// In fact, space for the whole object instance is allocated on the heap.
public class VariableExamples {
// Static variable allocated in global area.
static int b = 1;
// NOTE: parameter variable argv
public static void main (String[] argv)
{
// Local variable 'c' allocated on the stack.
int c = 2;
// The value in 'c' gets copied into the parameter variable (see below).
print (c);
// Space for the whole object is allocated on the heap.
MySpecialObject obj = new MySpecialObject ();
// Access variables inside the object via variable name and '.' operator.
obj.a = 3;
print (obj.a);
// When the method exits, 'c' and 'obj' both disappear.
}
// Parameter variable x is on the stack.
static void print (int x)
{
System.out.println ("x=" + x);
// You can treat the parameter like any variable.
x = 4;
// Static variable 'b' is accessible here.
System.out.println ("b=" + b);
// When the method exits, 'x' disappears.
}
}
State and Tracing State
Consider the following code:
public class StateExample {
// Static variable allocated in global area.
static int q = 1;
// NOTE: Java's static keyword does NOT mean the value can not change
public static void main (String[] argv)
{
// Local variable 'p' allocated on the stack.
int p = 0;
// when p is overwritten with a new value, its state has changed
p = 100;
// when any variable is overwritten, its state is changed
q = -1;
// as variables change, the program's state also changes
}
}
Let's diagram the memory for the above program through its execution. Diagraming of this sort is often called a memory trace or just a trace of the program. Generating a memory trace is typically called tracing the program. Note that comments and white space are not processed in Java, so processing skips a few lines from the code when the program runs.
Immediately after the first statement on line 11 is processed, StateExample has the following state:

We will identify the memory area for each variable in our memory traces.
Of course, this program does not stop after processing line 11, so it proceeds through the remaining statements.
Immediately after the statement on line 14 is processed, StateExample has the following state:

Immediately after the statement on line 16 is processed and through the end of the program, StateExample has the following end state:
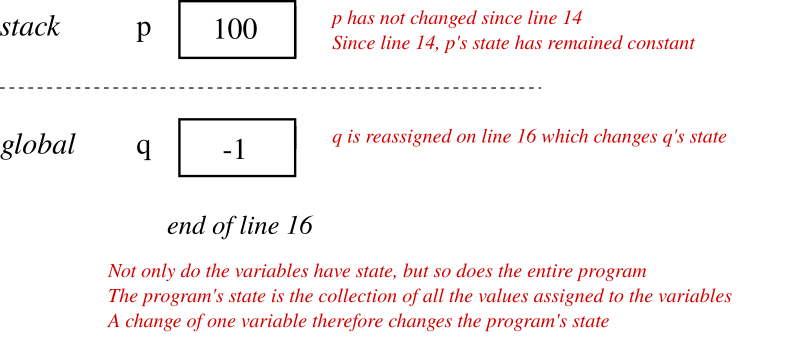
In this course, we will use the following model for tracing memory diagrams.
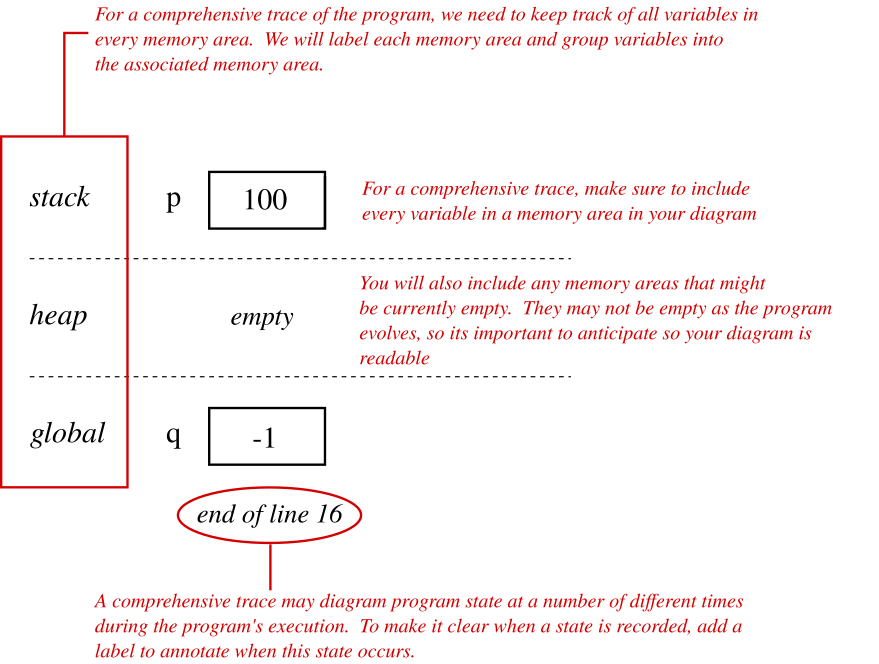
This memory trace model will evolve a bit as we come to understand the roles and behaviors of the different memory areas; however, the first step we will take is to condense the diagram to trace multiple states so we can see the big picture. For example, we can combine the individual states of the program into a single diagram to see how the state evolves over the entire runtime of the program.

Tracing involves performing an analysis on the state of the program over some timespan:
- In this context, state means the association between the condition or status of something with respect to time.
- State can refer to the value stored in an individual variable or the collective values stored in all variables for an entire object or even an entire program.
- We might also use the term evolve when discussing state because of the expectation of change with respect to time.
- Many terms in computer science implicitly relate to state. For example:
- variable describes a memory location that can change over the lifespan (a time span) of that variable.
- constant describes a memory location that can never change once it is initialized. Note that "never" is a time constraint.
- When we debug, we generally revert back to tracing the state of one or more variables.
Base 2 Powers and Logarithms
Take a minute to consider this table that expresses some of the integer powers and logarithms of base 2.
| 20 = 1 | log21 = 0 |
| 21 = 2 | log22 = 1 |
| 22 = 4 | log24 = 2 |
| 23 = 8 | log28 = 3 |
| 24 = 16 | log216 = 4 |
| 25 = 32 | log232 = 5 |
| 26 = 64 | log264 = 6 |
| 27 = 128 | log2128 = 7 |
| 28 = 256 | log2256 = 8 |
| 29 = 512 | log2512 = 9 |
| 210 = 1024 | log21024 = 10 |
| 211 = 2048 | log22048 = 11 |
| 212 = 4096 | log24096 = 12 |
| 213 = 8192 | log28192 = 13 |
| 214 = 16384 | log216384 = 14 |
| 215 = 32768 | log232768 = 15 |
| 216 = 65536 | log265536 = 16 |
This is clearly mathematics, but look beyond the math and consider what concept and in particular what pattern is being expressed by the math.
For instance, the powers table expresses a doubling effect. Each step down the table is double the previous entry. This is a form of growth, colloquially called exponential growth. This type of growth is seen very often in nature. For instance, this growth function roughly models the rate of cell division during reproduction or the rate of viral infection through a population. Could the power function have some use to us when modeling problems in computer science?
The logarithmic table expresses the opposite effect, or a halving effect. In the integer domain, the base 2 logarithm predicts the maximum number of times something can be divided in half until it can no longer be subdivided. Many things are discrete, so the logarithm similarly helps to predict decay rates down to termination of the process. For example, a logarithmic function models radioactive half-life, "half-life" is the time for half the material to decay, because it is an analysis and prediction of two halves, i.e. how long until half the material is decayed and half the material remains. Does the logarithmic function have some use for us to model a problem in computer science?
Sizing an array
The following example shows a variety of ways through which
an array is given a size:
import java.util.*;
public class ArraySize {
public static void main (String[] argv)
{
// Hard-coded size.
int[] A = new int [5];
System.out.println ("Array A has size " + A.length);
// Use a variable, and assign the variable a value.
int size = 6;
int[] B = new int [size];
System.out.println ("Array B has size " + B.length);
// Have the size determined elsewhere.
size = getSize ();
int[] C = new int [size];
System.out.println ("Array C has size " + C.length);
// Unknown size until run-time.
size = getSizeFromScreen ();
int[] D = new int [size];
System.out.println ("Array D has size " + D.length);
}
static int getSize ()
{
return 7;
}
static int getSizeFromScreen ()
{
System.out.print ("Enter size: ");
Scanner scanner = new Scanner (System.in);
return scanner.nextInt ();
}
}
In-Class Exercise 4:
Use the above program to find the largest array you can allocate.
Try to get the size accurately (down to the last digit).
Keep track of how many times you run the above program.
Depending on your strategy, this process could take a long time. What would be an effective strategy to minimize the number of times that you need to run the program? Describe your strategy.
Hints:
- DO NOT increment by one. If you have 16 GB of memory and start at an array size of 1, it would take roughtly 4 billion guesses to determine the maximum size.
- The powers of 2 table above should suggest a strategy that is guaranteed to find the largest array in less than 64 attempts.
In a later module, we will discuss algorithms that divide a problem in two and then solve each subdivided problem with a subroutine. This is called a 'divide-and-conquer' strategy and the base 2 logarithm will play an important role when we analyze these particular strategies.
Primitive or Reference Types
There are only two fundamental types of variables: primitive types and reference types.
Consider this example:
public class ReferenceExample {
public static void main (String[] argv)
{
int x = 16;
// Note: x is a primitive type.
int[] A = {1, 2, 3, 4, 5};
// Note: A is really a reference type that refers to an array.
}
}

Note:
- Primitive types are the basic data types provided by a programming language. In Java there are eight primitive data types: byte, short, int, long, float, double, boolean, and char.
- In the above example, x is declared as type int which is a primitive type.
- A variable that is declared as a primitive type labels or names a memory location for ease of use. This simple convention allows a programmer to associate names or labels with values rather than having to associate memory addresses with values.
- In Java, reference types are any non-primitive type. For example, arrays and objects are really reference types.
- In the above example, the declaration of A appears to suggest that A is an array. However, A is actually a reference to an array of int's. The value stored in the variable A is the address of the array.
- The terms reference and pointer are often used interchangably. A reference stores the address of another location in memory (where the data is actually stored) rather than data itself, and as such, we may say a reference "refers" or "points" to an object in memory.
- The reference model is used because it allows us to easily change where a pointer points. The benefits of this model will become more evident with more experience.
String examples
Consider this example:
public class StringExample {
public static void main (String[] argv)
{
// Pangram: a sentence with at least one occurence of each letter 'a' to 'z'.
// Direct creation of String array with constants.
String[] pangramWords = {"two", "driven", "jocks", "help", "fax", "my", "big", "quiz"};
// Note: pangramWords is a pointer.
// Count total length of all words.
int totalChars = 0;
for (int i=0; i < pangramWords.length; i++) {
// Here we are using String's length() method.
totalChars += pangramWords[i].length();
}
System.out.println ("Total #letters in pangram: " + totalChars);
}
}
Note:
- When the array is created, the variable pangramWords
points to a section of the heap with space for 8 string variables.
- The variable pangramWords is itself in
stack memory, where local variables are placed.
- String's are objects; an array of String's
is represented a little differently than an array of int's.
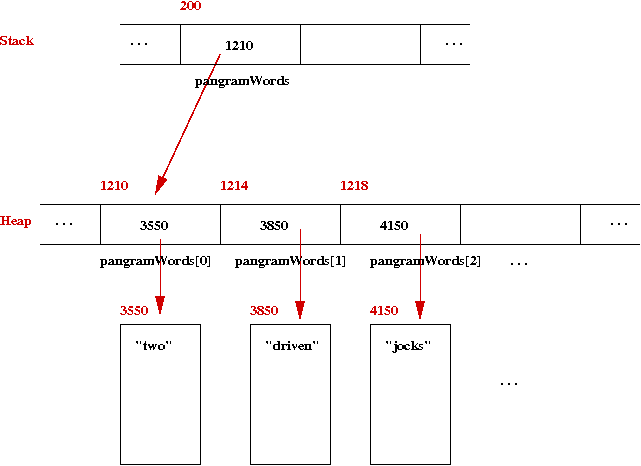
- Clearly, pangramWords is a pointer to a chunk of
memory that has 8 spaces (length of array).
- But 8 spaces of what?
- It turns out, 8 spaces of pointers to String's.
- Thus, each array entry is actually a pointer to a chunk of
memory (at yet another heap location) that holds a String.
- In general, object instances are chunks of memory
in the heap.
Let's look over another example: we'll identify the number of
words in our dictionary that begin and end with the same letter:
public class StringExample2 {
public static void main (String[] argv)
{
// Get the list of words.
String[] words = WordTool.getDictionary ();
int num = 0;
for (int i=0; i < words.length; i++) {
// Extract first and last char's and check equality.
char firstChar = words[i].charAt (0);
char lastChar = words[i].charAt (words[i].length()-1);
if (firstChar == lastChar) {
num ++;
}
}
System.out.println ("Number of words with same first and last char: " + num);
}
}
In-Class Exercise 5:
Write code to verify that a pangram is indeed a pangram
(has all the letters). Start by reading this Analysis of the Pangram algorithm and then download
this template.
You will find these facts useful:
- To convert from a char to an int:
int start = (int) 'a';
- To go the other way:
char ch = (char) start;
- To see if a letter exists in a String:
int index = words[j].indexOf (ch);
if (index >= 0) {
// Yes, it's there.
}
To make use of the above facts, you may need to familiarize yourself with the ASCII Table which determines how letters (and numbers) are represented in a string.
Random arrays
Why random arrays?
- They're useful in creating test data to test array code.
- Some interesting problems can be solved using randomly
generated arrays.
First, let's see how we can create them:
(Also needed: (UniformRandom.java)
import java.util.*;
public class RandomArray {
public static void main (String[] argv)
{
// Generate 10 random integers, each between 1 and 100
int[] randomInts = new int [10];
for (int i=0; i < randomInts.length; i++) {
randomInts[i] = UniformRandom.uniform (1, 100);
}
// Print.
System.out.println ( "Array elements: " + Arrays.toString(randomInts) );
// Generate 10 random doubles between 1 and 100
double[] randomReals = new double [10];
for (int i=0; i < randomReals.length; i++) {
randomReals[i] = UniformRandom.uniform (1.0, 100.0);
}
// Print.
System.out.println ( "Array elements: " + Arrays.toString(randomReals) );
}
}
Next, let's solve this problem: what are the chances that a randomly
generated array of integers is already sorted?
public class RandomArray2 {
public static void main (String[] argv)
{
double p = estimateSortedProb (5, 100000);
System.out.println ("Probability an array of length 5 is sorted: " + p);
}
static double estimateSortedProb (int arraySize, int numTrials)
{
// Count the number of sorted arrays generated.
int numSorted = 0;
// Repeat for given number of experiments.
for (int n=0; n < numTrials; n++) {
// Generate a random array.
int[] randomInts = new int [arraySize];
for (int i=0; i < randomInts.length; i++) {
randomInts[i] = UniformRandom.uniform (1, 100);
}
// See if sorted.
boolean isSorted = true;
for (int i=1; i < randomInts.length; i++) {
if (randomInts[i] < randomInts[i-1]) {
isSorted = false;
}
}
if (isSorted) {
numSorted ++;
}
} //end-for-numTrials
// The fraction of trials that resulted in a sorted array:
double prob = (double) numSorted / (double) numTrials;
return prob;
}
}
In-Class Exercise 6:
The above code only checks that the array is sorted in
increasing-order. Add code to check whether it's sorted
in decreasing order. This way, we count both sorted-increasing
and sorted-decreasing as sorted.
Note: The general structure of such estimation problems is:
int numSuccessfulTrials = 0;
for (int n=0; n < numTrials; n++) {
doTrial ();
if (trialSuccessful) {
numSuccessfulTrials ++;
}
}
double probSuccess = (double) numSuccessfulTrials / (double) numTrials;
Next, let's use random arrays to solve the famous "Birthday Problem":
in any group of N people, what are the chances that at least two of them
share a birthday?
public class Birthday {
public static void main (String[] argv)
{
double p = birthdayProblem (10);
System.out.println ("Prob[shared birthday with 10 people] = " + p);
}
static double birthdayProblem (int numPeople)
{
// Number of times to repeatedly create a random group of people:
int numTrials = 10000;
// We'll need to count how often we get a shared b'day.
int numTrialSuccesses = 0;
// Repeat and count.
for (int n=0; n < numTrials; n++) {
// Generate birthdays (random array)
int[] birthdays = new int [numPeople];
for (int i=0; i < birthdays.length; i++) {
birthdays[i] = UniformRandom.uniform (1, 365);
}
// Check if any two match.
boolean matchExists = false;
for (int i=0; i < birthdays.length; i++) {
for (int j=0; j < birthdays.length; j++) {
if ( (i != j) && (birthdays[i] == birthdays[j]) ) {
// Note: musn't forget the i!=j test above!
matchExists = true;
}
}
}
if (matchExists) {
numTrialSuccesses ++;
}
} //end-for-trials
double prob = (double) numTrialSuccesses / (double) numTrials;
return prob;
}
}
In-Class Exercise 7:
How many people are needed for a better than 50% chance
of seeing a shared birthday?
Download Birthday.java
and UniformRandom.java and find out.
Algorithms
What is an algorithm?
- A way to solve a problem computationally.
- It is NOT code, although code can sometimes serve as
a way to describe an algorithm.
- Algorithm's are conceptual, not tied to a language like Java.
Algorithms are usually described as simply as possible.
- For example, we described the "estimation" algorithm as:
int numSuccessfulTrials = 0;
for (int n=0; n < numTrials; n++) {
doTrial ();
if (trialSuccessful) {
numSuccessfulTrials ++;
}
}
double probSuccess = (double) numSuccessfulTrials / (double) numTrials;
- We could simplify this further into an English-like
description:
1. Repeat N times (steps 2 and 3):
2. Perform trial;
3. If trial is successful, increment count
4. estimate = count / N
- Or, we could use so-called "pseudocode"
1. count = 0
2. trialNum = 0
2. repeat
3. isSuccess = performTrial ();
4. if (isSuccess)
5. count = count + 1
6. endif
7. trialNum = trialNum + 1
8. while (trialNum < N)
9. return (count / N)
- There is no standard for describing algorithms:
- Generally, you try to remove language-specific detail.
- You want to keep the key ideas of the algorithm intact.
© 2006-2020, Rahul Simha & James Taylor (revised 2020)