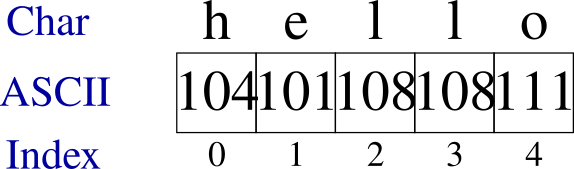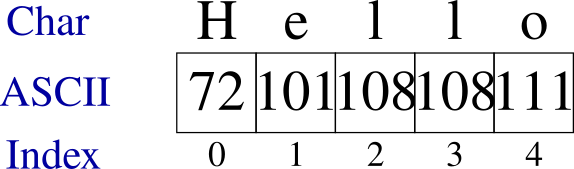Module 1 Supplement : The Ascii Table
ASCII
Recall that a computer stores everything using a numeric value. In fact, your computer stores everything in a binary representation, i.e. a sequence of ones and zeroes. It it understandable if it is not obvious how ones and zeroes can represent all the characters in the English language let alone characters and symbols from other languages. Fortunately, the average user does not need to even consider binary and can instead think in a more familiar representation like alpha-numerics.
A programmer, on the other hand, should at least be familiar with the decimal, i.e. base ten, representation of numbers for a number or reasons:
- A programmer should understand the concept of encoding and decoding. To encode is to convert from one representation into a coded form and to decode is to convert from a coded form back to its original representation.
- A programmer may be able to convert a string problem into a simpler math problem which might produce a much simpler, efficient, and reliable algorithm.
English speakers are very familiar with the alphabetical symbols and arabic numerics standard to the English language; however, more symbols are necessary to faithfully represent English grammar and to format how information is printed to a device. For example, we don't necessarily think of symbols like a 'space' or punctuation marks as a part of the English alphabet, but they are critical elements of written English grammar.
ASCII is an abreviation for American Standard Code for Information Interchange and it is a standard for the encoding of character symbols commonly used in the written English language. It not only encodes the alphabet and numerics ('alpha-numerics') standard to the English language but also the other printing symbols such as the dollar sign, quotation marks, parentheses, etc. as well as a number of non-printing command characters that control formatting on a printing device.
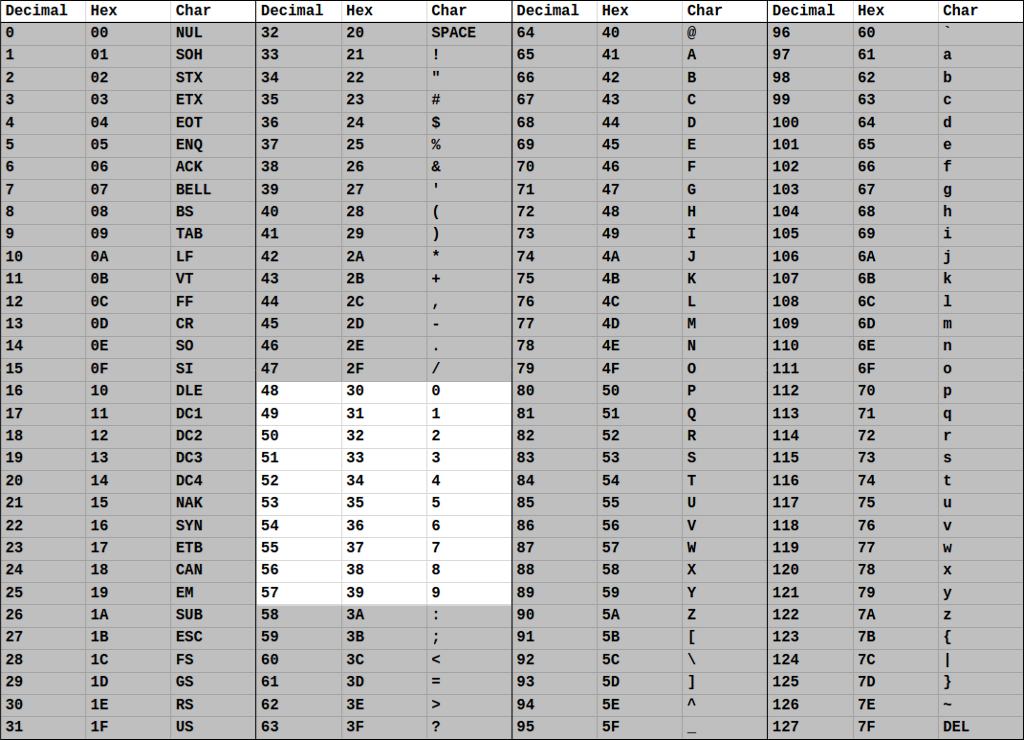
The ASCII table below illustrates each value and its associated character code when encoding and decoding English character symbols:
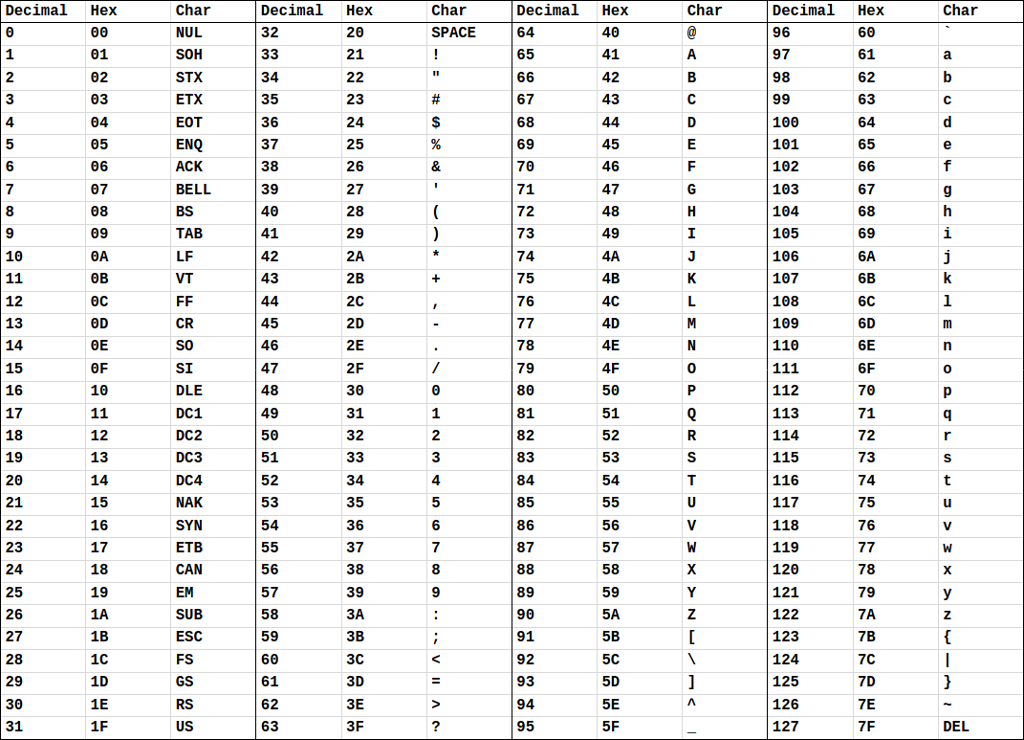
ASCII Command Codes
The first values 0-31 are command characters. Most command characters are unprintable, i.e. they don't have an associated visual symbol to print, and they are used to issue control commands or to control formatting on the printing device.
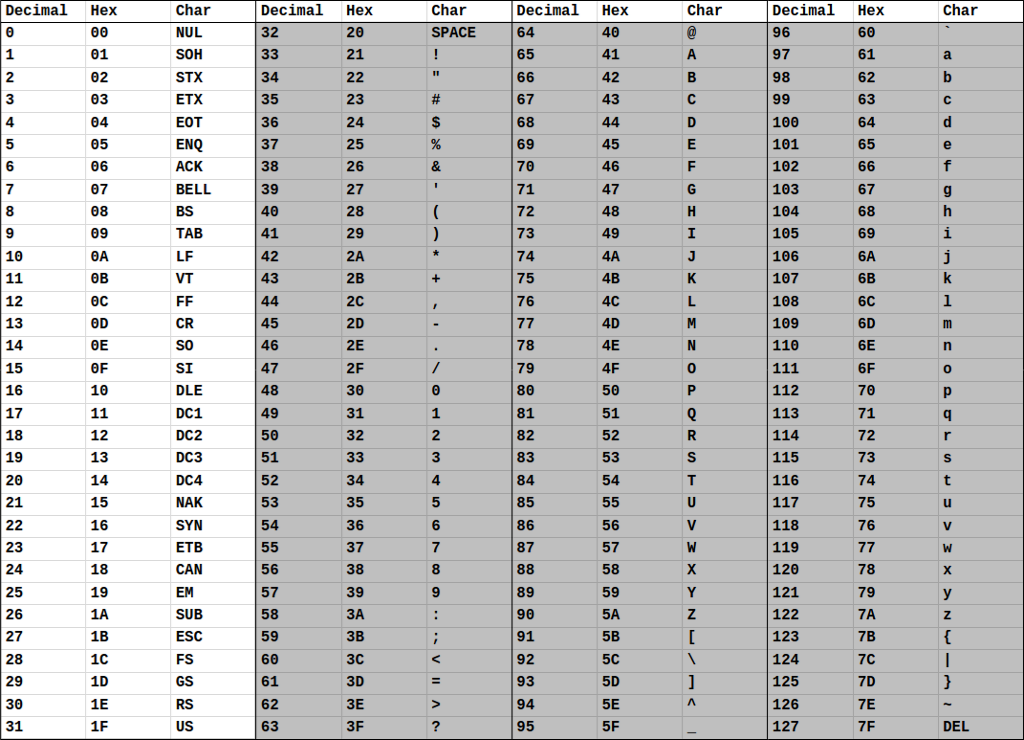
Many of these are now irrelevant as they have been rendered defunct or redundant for much of the modern technology we use today. However, some command codes remain exceedingly important:
- Tab (Decimal value 9) represents the horizontal tab character that is generated when the Tab key on the keyboard is struck. In Java, the /t character generates a Tab character in code.
- Linefeed (Decimal value) is used by some systems to represent the vertical spacing generated by the Return key.
- Carriage Return (Decimal value 13) is used by some other systems to represent the same verical spacing generated by the Return key as Linefeed.
Why do two symbols/values represent the return behavior. Well the developers of Unix decided to use one approach, then Apple decided to use a different approach, and Microsoft decided to use yet another approach. Most of the time, this difference is not a significant issue, but it can come up in some important applications such as when reading and writing files. The good news is that in Java the /n character is replaced with the correct variant for the system the program is running on.
ASCII Numeric Characters
When you type a zero character, your computer is not storing actually storing a zero value but is instead storing the decimal value 48. To store that input as the numeric value of zero, the string data must be converted to a numeric data type like an int. The program/subrouting that performs this conversion examines each digit in the string sequence of characters and performs the math to add the characters up into a number then returns that value so it can be stored in a single location. This subrouting of course only works if that string can legally be converted to a number.
Numbers in strings are represented very differently than values declared with a specific numeric type. For example, a variable declared as an int will be stored as a numeric value in a single location in memory while a number in a string is a sequence of individual digits with each digit stored in different locations in memory.
TODO : An image of a number in memory vs. a string of numbers.
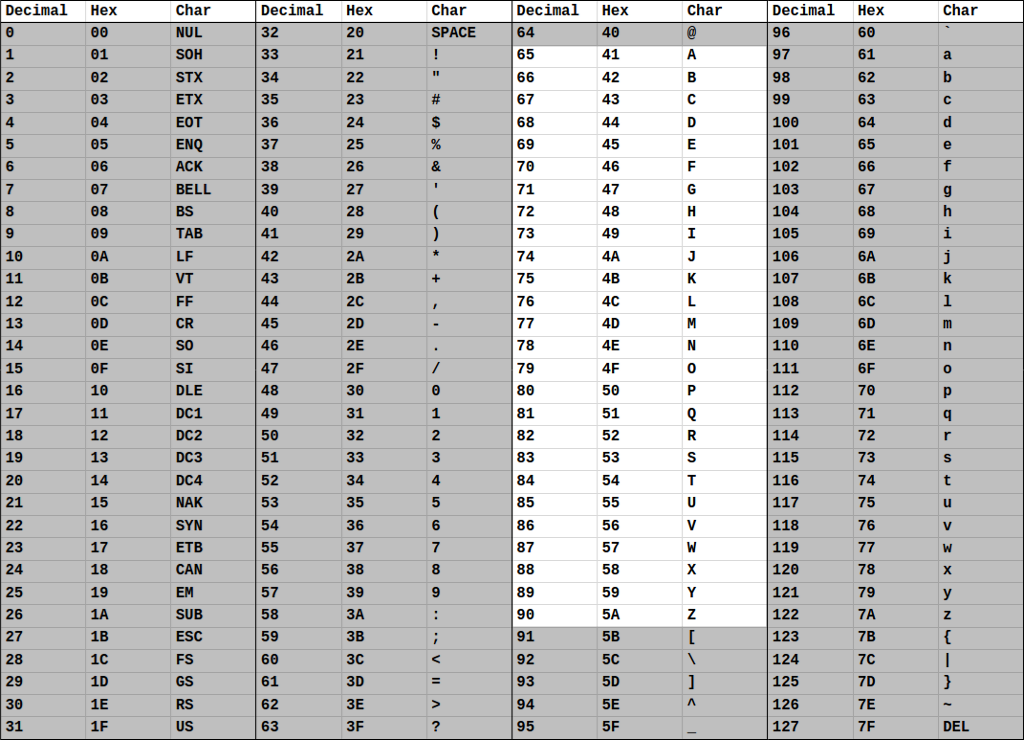
ASCII Uppercase Alpha Characters
The range of uppercase alpha characters in the ASCII table begins at 'A', represented in decimal as 65, and represents the remaining uppercase alphabet in sequence up to 'Z', decimal 90. The difference between the decimal representations of 'Z' and 'A', i.e. 90-65, is 25. You might anticipate this difference to be 26, there are 26 characters in the alphabet after all; however, this is a case where subtracting has caused our counting to begin with zero rather than one. By subtracting 'A' from 'Z' we have effectively defined our number system in the range [0, 25] rather than [1, 26]. This might have some benefits because it maps really well to the addressing system used for arrays.
ASCII Lowercase Alpha Characters
The range of lowercase alpha characters in the ASCII table begins at 'a', decimal 97, and maintains the entire lowercase alphabet in sequence up to 'z', decimal 122. Just like with the uppercase alpha characters, subtracting 'a' from 'z', i.e. 122-97, yields the expected value of 25.
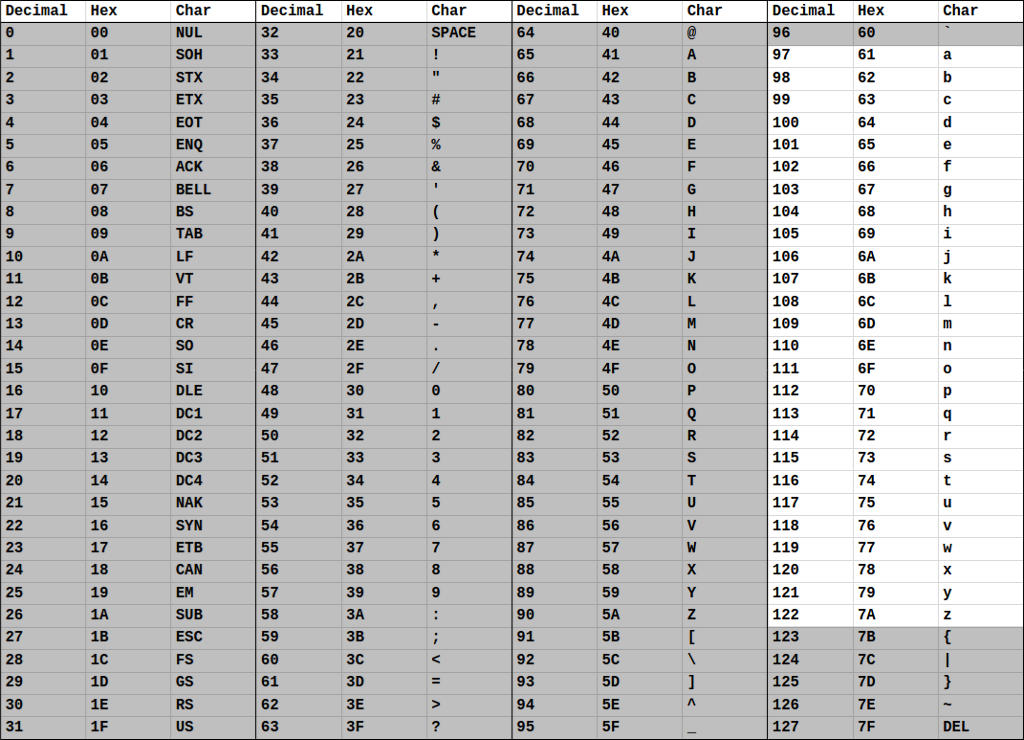
Take a close look at both the uppercase and lowercase sections of the ASCII table. Specifically, look at the offset (the difference between) the decimal representations of 'A' and 'a'. You should see that they (and every uppercase and lowercase alpha) have an offset of exactly 32. This means that to convert from uppercase to lowercase, you can simply add 32 to the uppercase value. Similarly, to convert from lowercase to uppercase, you can subtract 32 from the lowercase value. This converts and greatly simplifies our problem of moving between uppercase and lowercase characters. Consider that this is now a very simple and hard to break math problem and it avoids the need for a complex and brittle algorithm that relates two abstract symbols like 'A' and 'a' or 'Z' and 'z'.
String Examples
Let's assume that we are working on a program that stores a string containing the word 'HELLO'. Internally, the string will be stored using the following ASCII representation:
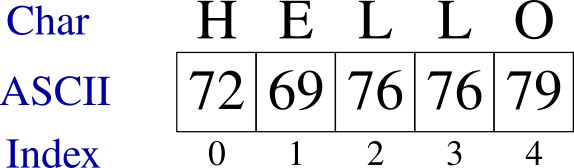
If instead, we changed the string to store the lowercase version of the same string, it would instead be stored with the following ASCII values:
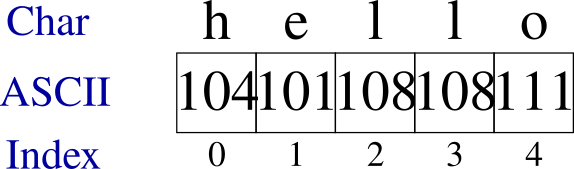
If the string mixed uppercase and lowercase letters, then it would be represented as the following:
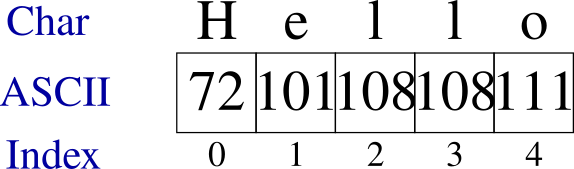
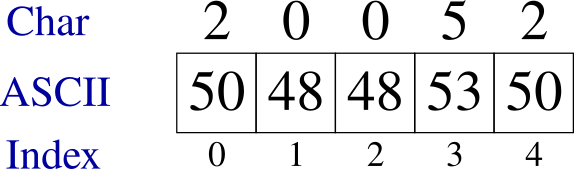
For a numeric string, the string looks nothing like the number that is represented and this example illustrates how different the string representation is of a number is from its numeric value.
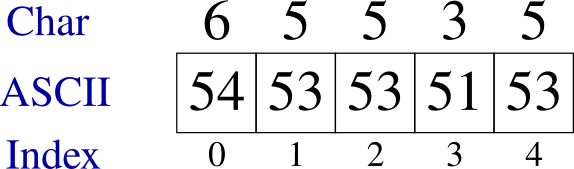
The ASCII representation of numbers can be more expensive in terms of space. For example, the number in the following example requires five bytes because each character requires a byte while it can be representing in an integer format of two to four bytes.
As suggested earlier, you cannot perform math natively on numbers in string format. If you need to perform a mathematical calculation, you will need to first perform a calculation that computes the integer (or other legal numeric format) representation of the numeric characters in the string.
© 2006-2020, Rahul Simha & James Taylor (revised 2021)