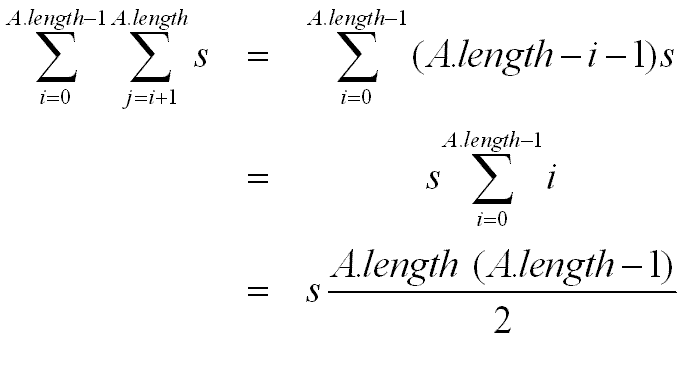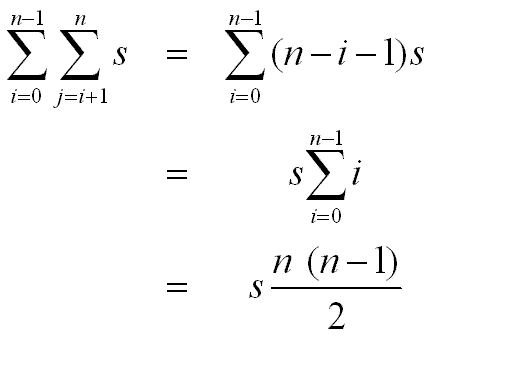Module 1: Introduction
For reference, see original material on Prof.Simha's website, Module 1,
from
which this material is taken
Improving a program's speed
Consider the following simple problem:
- Input: an array of numbers.
- Output: the two numbers whose absolute difference is largest,
and the absolute difference.
As a first attempt to solve this problem, consider
(source file):
static void algorithm1 (double[] A)
{
// 1. Set the initial maximum to the difference between the first two:
double max = Math.abs (A[0] - A[1]);
// 2. Record the actual values:
double x = A[0], y = A[1];
// 3. Now compare each pair of numbers:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
// 3.1 For each such pair, see if it's differenceis larger
// than the current maximum.
double diff = Math.abs (A[i] - A[j]);
if (diff > max) {
// 3.1.1 If so, record the new maximum and the values
// that achieved it.
max = diff;
x = A[i];
y = A[j];
}
} // inner-for
} // outer-for
// 4. Output:
System.out.println ("Algorithm 1: the numbers: " + x + "," + y
+ " difference=" + max);
}
Here are some timings for different array sizes (in milliseconds):
| Array size | execution time |
| 1000 | 84 |
| 2000 | 258 |
| 3000 | 554 |
| 4000 | 985 |
| 5000 | 1551 |
| 6000 | 2228 |
| 7000 | 3031 |
| 8000 | 3962 |
| 9000 | 5020 |
| 10000 | 6247 |
How could we improve this program?
- Write it in a faster language, e.g. C.
- Seek algorithmic improvements.
Write it in a faster language, e.g. C.
(source file):
Here are some timing comparisons (in milliseconds):
| Array size | Java (Algorithm1) | C |
| 7000 | 3031 | 2670 |
| 8000 | 3962 | 3490 |
| 9000 | 5020 | 4430 |
| 10000 | 6247 | 5490 |
So, it is faster. Can we improve it further?
In-Class Exercise 1.1:
(Solution)
In what other ways can the original Java program be improved?
Now let's consider some algorithmic improvements:
- Algorithm 2:
(source file):
static void algorithm2 (double[] A)
{
// 1. Sort the array:
Arrays.sort (A);
// 2. The smallest is first, the largest last:
double diff = A[A.length-1] - A[0];
// 3. Output:
System.out.println ("Algorithm 2: the numbers: " + A[0] + "," + A[A.length-1]
+ " difference=" + diff);
}
Now compare this with Algorithm1 (in Java) and the algorithm in C:
| Array size | Algorithm1 (Java) |
Algorithm1 (C) | Algorithm2 (Java) |
| 7000 | 3031 | 2670 | 47 |
| 8000 | 3962 | 3490 | 49 |
| 9000 | 5020 | 4430 | 49 |
| 10000 | 6247 | 5490 | 56 |
- Algorithm 3:
(source file):
static void algorithm3 (double[] A)
{
// 1. Initialize min and max:
double min = A[0];
double max = A[0];
// 2. Scan through array finding the latest min and max:
for (int i=1; i < A.length; i++){
if (A[i] < min)
min = A[i];
else if (A[i] > max)
max = A[i];
}
// 3. Output:
double diff = max - min;
System.out.println ("Algorithm 3: the numbers: " + min + "," + max
+ " difference=" + diff);
}
In-Class Exercise 1.2:
(Solution)
Why are algorithms 2 and 3 faster?
A more complex problem and some solutions
Consider the largest distance problem:
- Input: a set of points on the place (x and y values for each point).
- Output: the distance between the two points that are furthest apart.
- Sample application: enclosure/aperture design.
In-Class Exercise 1.3:
(Solution)
In this exercise you will write code to find the distance
between the two furthest points among a set of points:
In-Class Exercise 1.4:
(Solution)
Take your code for Exercise 3, and count the number of times "distance"
is computed. For n points, how many times
is distance computed?
Now consider this algorithm:
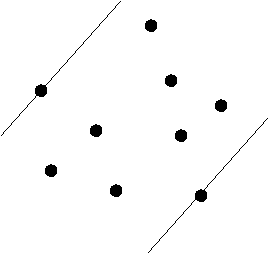
- First, compute the convex hull of the set of points.
- Then, scan the hull and find antipodal pairs.
- Compute the distances between antipodal pairs.
- Report the largest such distance.
Let's take this one step at a time:
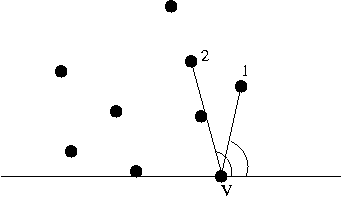
- What is a convex hull?
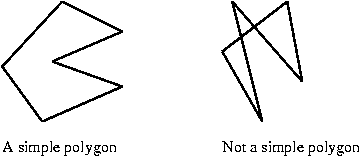
- First: a (simple) polygon is an ordered
set of edges such that successive edges and only
successive edges share a single endpoint.
In other words, a polygon is a curve ending on itself
that is formed by a sequence of straight-line segments. A simple
polygon does not cross itself.
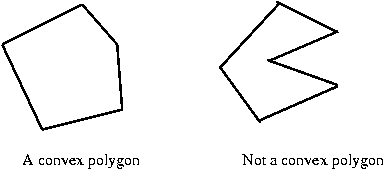
- Second: a polygon is convex if no internal
angle is larger than 180 degrees.
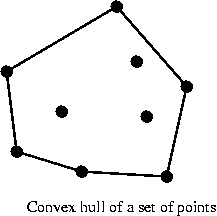
- Finally: for a set of points, the convex hull is the
smallest convex polygon completely enclosing the points.
- Using the Graham-Scan algorithm to compute the convex
hull:
- Find distances between antipodal pairs:
Now, let's take a first look at the code:
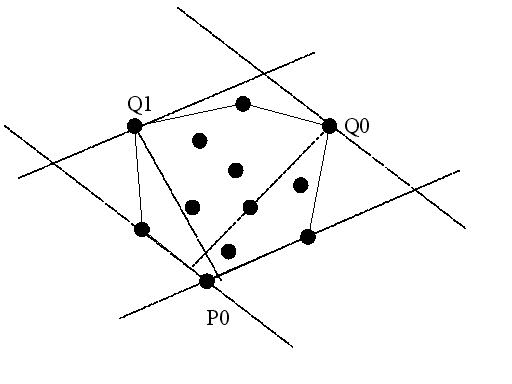
- The AntiPodal Algorithm:
(source file):
public class AntiPodalAlgorithm {
public static double findLargestDistance (Pointd[] points) {
// 1. Compute the convex hull:
Hull grahamHull = new Hull(points);
// 2.1 Extract the hull points:
Pointd[] hullPoints = grahamHull.getHull();
// 2.2 Extract the number of points in the hull (hullSize):
int hullSize = grahamHull.getSize();
// variables to be used.
double largest=0.0;
int q0, q1, q2, i=0;
// 3.0 Find the farthest point to size s0 of the hull
// incident at points[hullSize-1] and points[0]:
while (Geometry.area(hullPoints[hullSize-1], hullPoints[0], hullPoints[i])
< Geometry.area(hullPoints[hullSize-1], hullPoints[0], hullPoints[(i+1)%hullSize]))
i++;
q0 = i;
// 3. Find farthest points to other sizes of the hull.
// Compute largest distance:
for (int j=0; j < hullSize-1; j++) {
// 3.1 Find farthest points:
while (Geometry.area(hullPoints[j], hullPoints[j+1], hullPoints[i % hullSize])
< Geometry.area(hullPoints[j], hullPoints[j+1], hullPoints[(i+1) % hullSize]))
i++;
q2 = i;
q1 = i;
// 3.2 Now the antipodal points of hullPoints[j] are between q0 and q1, inclusive.
// Compute the largest distance between antipodal pairs containing hullPoints[j]
while (!(q2 < q0)) {
largest = Math.max(largest,
Geometry.distance(hullPoints[j], hullPoints[q2 % hullSize]));
q2--;
}
q0 = q1;
}
return largest;
}
}
- Computing the convex hull:
(source file):
import java.util.*;
public class Hull {
// Maintain hull points internally:
private Pointd[] hull;
private int hullSize;
// Constructor that takes the point set:
public Hull (Pointd[] points) {
Pointd[] vertices;
int i, n;
// record the number of points in the point set:
n = points.length;
// 0. Make a copy of the vertices because we'll need to sort:
vertices = new Pointd[n];
for (i=0; i < n; i++)
vertices[i] = new Pointd();
System.arraycopy (points, 0, vertices, 0, n);
// 1. Find the leftmost, lowest point (it is on the hull):
int low = findLowest(vertices);
// 2.0 Put the low in the first position:
swap (vertices, 0, low);
// 2.1 Sort vertices based on their polar angles in counterclockwise
// order around the leftmost lowest point.
HullSortComparator comp = new HullSortComparator(vertices[0]);
Arrays.sort(vertices, 1, vertices.length-1, comp);
// 3. Remove collinear points:
n = removeCollinearPoints(vertices);
// 4. Compute the Hull based on Graham's Scan:
hull = grahamScan(vertices, n);
}
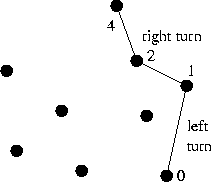
private Pointd[] grahamScan(Pointd[] points, int numOfPoints) {
// 1. Create a stack and initialize with the first three points:
HullStack hstack = new HullStack (numOfPoints);
hstack.pushNew(points[0]);
hstack.pushNew(points[1]);
hstack.pushNew(points[2]);
// 2. Start scanning points:
for (int i=3; i < numOfPoints; i++) {
// 2.1 isHull check whether the top two points in the stack and the point
// this is scanning form a right turn or not.
// if right turn, then pop the top element.
while (!hstack.isHull(points[i]))
hstack.popTop();
// 2.2 Push the point that is just scaned into the stack.
hstack.pushNew(points[i]);
}
// 3. Return all points still on the stack:
hullSize = hstack.getSize();
return hstack.hullArray();
}
// Compute the lowest point (the point with smallest y-coordinate). Choose
// the leftmost one in case of a tie.
private int findLowest (Pointd[] points)
{
// 1. Scan through points:
// 1.1 If y-value is lower, the point is lower. If the y-values
// are the same, check that the x value is further to the right:
// 2. Return lowest point found:
}
// Compute the lowest point (the point with smallest y-coordinate). Choose
// the leftmost one in case of a tie.
private int findLowest (Pointd[] points) {
// Not shown
}
// Swap two points.
private void swap (Pointd[] points, int i, int j) {
// Not shown
}
}
Next, consider this idea:
- Suppose experimentation reveals that the hull points are only a
small subset of all the points.
For example, we compute the number of hull points for the
following data sizes (randomly generated):
| # of points | # hull points |
| 10 | 6 |
| 100 | 13 |
| 1000 | 18 |
| 10000 | 25 |
- This suggests computing the hull and then doing an all-pairs
distance computation:
(source file):
public class HullAlgorithm {
public static double findLargestDistance(Pointd[] points) {
double diffX, diffY, dist, largest = 0.0;
// 1. Compute the convext hull:
Hull grahamHull = new Hull(points);
// 2.1 Extract the hull points:
Pointd [] hull = grahamHull.getHull();
// 2.2 Extract the hull size:
int size = grahamHull.getSize();
// 3. Compute largest distance between hull points:
for (int i=0; i < size; i++) {
for (int j=i+1; j < size; j++) {
diffX = hull[i].x - hull[j].x;
diffY = hull[i].y - hull[j].y;
dist = Math.sqrt(diffX*diffX + diffY*diffY);
// largest = Math.max(largest, dist);
if (largest<dist)
largest = dist;
}
}
return largest;
}
}
Note:
- Fact: the AntiPodal algorithm is provably fast (fastest
possible, in a worst-case sense).
- Fact: the Hull algorithm is experimentally fast, but not
provably so. --because the hull size is small.
- Fact: it is possible to create pathological test data that makes the Hull
algorithm perform badly.
Summary:
- It is possible to design much faster algorithms using
insight into problem structure.
- A fast algorithm may be slow for small data sets, and might
require some setup overhead.
- A fast algorithm may be quite complicated, and use complicated
data structures.
- Some experimentation with typical data sets may reveal simpler
approaches that are as effective as the provably-fast algorithms.
Course outline
What this course is about:
- Part of the "science" in "computer science".
- Algorithm analysis: both for execution time and other
resources (like memory) (time and space).
- Problem-solving techniques.
- Performance monitoring and code tuning.
- Exposure to classic computer science problems and techniques.
- Exposure to useful data structures.
- Exposure to important types of combinatorial objects (graphs,
strings, geometry).
- Exposure to discrete optimization problems.
- Writing clean, efficient code.
In addition, you will:
- Learn to think about problems and algorithms independent of code.
- Improve your analytic skills.
- Improve your programming skills:
- More challenging debugging (e.g., "tree" code).
- Reusable code.
- Think at the right level of detail.
- Increase your ability to learn new material by yourself.
Key principles:
- Insight: Analysis of problem structure.
- Data organization: possibly sort the data, use an
efficient data structure.
- Divide and conquer:
- Breakdown the problem in the "right" way
- Solve smaller problems first.
- Put together solution from sub-solutions.
- Simple, effective code:
- Exploit the power of recursion.
- Reusable data structures.
- Simple, clear interfaces to data structures, and subproblem algorithms.
Algorithms in the context of the rest of computer science:
- The science of algorithms is a key computer science technology.
- Hard problems have been analysed and clever algorithms have
made some computations routinely fast.
Example: sorting
- A large class of (but not all) algorithms go hand-in-hand with
data structures.
These data structures tend to be used again and again.
- Often, some applications demand slight modifications in data structures.
(So, it's not enough to use a package).
- Algorithmic insight is a key skill.
- Algorithm analysis is an integral part of many other courses.
Algorithms
What is an algorithm?
- An algorithm is NOT a program.
- An algorithm is: the key ideas underlying a program that remain the same
no matter what language or machine is used.
- An algorithm sometimes consists of sub-algorithms
e.g., finding the convex hull is part of finding the largest distance.
- Algorithms are typically described in pseudocode.
- Algorithms are analyzed for speed independent of machine/language -- Asymptotic analysis.
- Algorithms are usually analyzed along with the problems they solve.
(Analyzing a problem is often harder).
Describing algorithms: pseudocode
What is pseudocode?
- A language-independent description of an algorithm.
- Various "levels" of pseudocode:
- Very-high level pseudocode, e.g., for Algorithm1 above:
1. Scan through all possible pairs of numbers in the array.
2. For each such pair, compute the absolute difference.
3. Record the largest such difference.
- English-like pseudocode:
Input: an array of numbers, A
1. Set the initial maximum to the difference between the first two
in the array.
2. Loop through all possible pairs of numbers:
2.1 For each such pair, see if it's difference is larger
than the current maximum.
2.1.1 If so, record the new maximum and the values
that achieved it.
3. Output the maximum found.
- Detailed pseudocode, as found in many algorithms books:
Algorithm1 (A)
Input: A, an array of numbers.
// Set the initial maximum to the difference between the first two:
1. max = Absolute-Difference (A[0], A[1]);
// Record the actual values:
2. x = A[0], y = A[1];
// Now compare each pair of numbers:
3. for i=0 to length-1:
4. for j=i+1 to length
// For each such pair, see if it's difference is larger
// than the current maximum.
5. diff = Absolute-Difference (A[i], A[j]);
6. if (diff > max)
// If so, record the new maximum and the values
// that achieved it.
7. max = diff;
8. x = A[i]; y = A[j];
9. end-if
10. end-for
11. end-for
Output: min, max, diff
Note:
- Such pseudocode usually does not contain variable
declarations or data-types
(they are usually implied or left to the reader)
- The pseudocode "language" is fictitious.
- Boldface is usually used for keywords.
- Not all methods/functions are shown, especially when
the meaning is obvious.
- Pseudocode (all levels) is extremely useful in describing algorithms.
- Notice how easy it is to express the key idea in high-level pseudocode.
- Recommended practice:
- Provide high-level pseudocode at the very minimum.
- Provide separate detailed pseudocode where possible,
usually in manuals or written documentation.
- Include the high-level pseudocode at the beginning
of a program.
- Include the detailed pseudocode as comments in the program.
Analysing algorithms
Algorithms are analysed using the so-called "order notation" or "asymptotic notation":
- The order-notation is initially confusing to learn.
- Once mastered, it makes analysis easier and definitely easy to present.
- The key idea: pay attention only to important details (dominating terms).
Consider the following example:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
double diff = Math.abs (A[i] - A[j]);
if (diff > max)
max = diff;
}
}
Let's analyse this piece of code:
- The outer loop is executed A.length-1 times.
- For the i-th outer loop iteration, the inner one is executed
A.length-i-1 times.
- In the inner loop, the Math.abs function is called every time.
- The assignment inside the if is not always executed.
- Assume it takes about s seconds in average for one iteration of the inner loop.
- How many seconds overall?
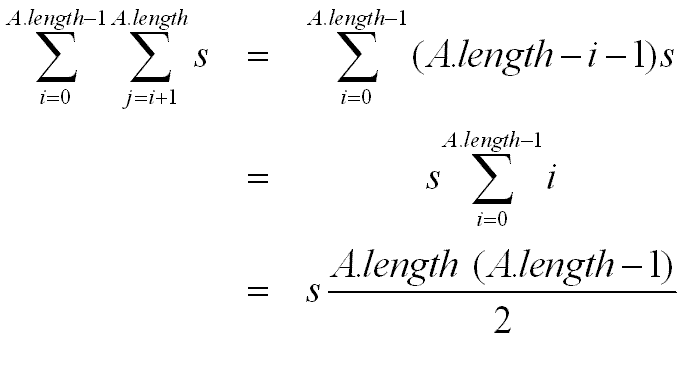
First, it's preferable to use math symbols:
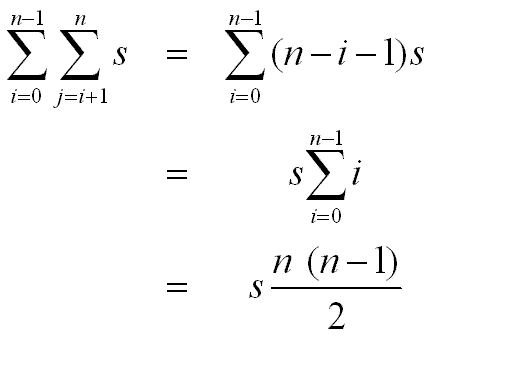
Nonetheless, it is possible to simplify further by observing that
n(n-2)/2 = n2/2 -2n/2.
Observe: the term that dominates is
n2/2.
Accordingly, for purposes of approximate analysis:
- Ignore the "lower-order" terms.
- Ignore constants.
=> The algorithm requires O(n2) steps.
The order notation
Let f(n) and g(n) be two functions defined on the reals:
- Definition:
We say f(n) = O(g(n)) if there exists positive constants
c and N such that f(n) <= cg(n)
whenever n > N.
- Translation: for large enough n, f(n)
grows no faster than g(n).
- How to say it aloud: f(n) is "Oh-of" g(n) or
"Big-Oh-of" g(n).
- Example: f(n)=10n and g(n)=n2.
- Example: f(n)=10n2 and g(n)=n2.
- The definition can use either "less than" or "less than or equal".
- Some additional definitions that require
math fonts (PDF version)
In-Class Exercise 1.5:
(Solution)
Find the c and N in the first definition above to show
that f(n)=6n2+18 is O(n2).
- Useful facts:
- If f1(n) = O(g1(n))
and f2(n) = O(g2(n))
then
- f1(n) + f2(n)
= max ( O(g1(n)), O(g2(n)) )
- f1(n) f2(n)
= O( g1(n) g2(n) )
- If f(n) = aknk + ak-1nk-1
+
... + a1n + a0
then f(n) = O(nk).
- Note:
- One does not unnecessarily overestimate, e.g., by saying
f(n)=10n2 = O(n4).
- Incorrect usage: f(n) < O(n2)
or f(n) <= O(n2).
- Don't provide a constant in the order: f(n) = O(5n2)
In-Class Exercise 1.6:
(Solution)
Implement and analyze the Selection Sort algorithm:
- SelectionSort works like this: Suppose the array is in
data[i].
First find the smallest element and put that in
data[0].
Then find the smallest element in the range
data[1],...,data[data.length-1]
and put that in
data[1], etc.
- Download SelectionSort.java
and UniformRandom.java.
- Write your code in the file SelectionSort,
to sort a data set of integers.
- Then test by executing SelectionSort.
- If f(n) denotes the number comparisons made by
SelectionSort for a data set of size n, what is the smallest
value of k for which f(n) = O(nk)?
- Count the number of comparisons - does your experimental
evidence match the analysis?
- Do the number of comparisons depend on the input data?
Worst-case and other comparisons
Consider comparing two algorithms A and B on the sorting problem:
- On some data sets A might perform better than B.
On others, B might perform better.
How to compare them?
- The standard approach: a worst-case order analysis:
- Other approaches:
- Best-case (theoretical)
- Average-case (theoretical)
- Average-case (experimental)
- Other kinds of issues:
- Complexity of implementation.
- Practical data sets, problem sizes.
- Relation to application, relative importance of algorithm.
- Exploiting architecture, operating systems.
Typical worst-case analysis:
- Assume the worst possible input for the algorithm.
- Identify key operations that take unit time.
- Count number of operations using order notation.
Theoretical average-case analysis:
- Assume a probability distribution over possible inputs.
- Derive expected running time using distribution.
- Express expected running time using order notation.
- Typically very difficult even for simple problems/algorithms.
- Not often practical, even if feasible.
Experimental average-case analysis:
- Compare algorithms on randomly generated data sets.
- Running a single algorithm sometimes makes little sense.
(Depends on processor, system architecture, OS).
- Create different types of data sets (uniform, non-uniform).
- Test over wide range of problem sizes.
- Accompany with worst-case analysis.
A comprehensive analysis of a problem:
- Prove a lower-bound on the problem.
(e.g., sorting cannot be solved faster than O(n log(n))
- Devise a fast algorithm.
- Analyse worst-case complexity of algorithm.
- Experimentally evaluate algorithm: compare with others and lower-bound.
- See if special cases can be solved faster.
Background math
A quick math review:
- What is a function?
- A formal definition requires more set-theory definitions.
- But we have an intuitive idea:
e.g., f(x) = x2 implies f(3) = 32 = 9.
- Informally:
- A domain of possible arguments - "what the function takes".
- A range - "what the function produces".
- For any argument, a unique result.
In-Class Exercise 1.7:
(Solution)
Use a calculator and plot the following functions in the range
(0,100) by "joining the dots" of function values computed
at 0, 10, 20, ..., 100:
- f(x) = x
- f(x) = x2
- f(x) = log2(x)
- f(x) = xlog2(x)
- f(x) = 2x
- f(x) = ex
- Useful exponentiation rules:
- xa xb = xa+b
- xa / xb = xa-b
- (xa)b = xab
- Logarithms:
- What exactly are they? - the "inverse of exponentiation"
- Definition: y = loga(x) if ay = x
- Example: What is log2(256)?
2? = 256?
28 = 256
Thus, log2(256) = 8.
- Another way of thinking about it:
- Divide 256 by 2 to get: 256 / 2 = 128.
- Then, 128 / 2 = 64
- ...
- How many times do we need to divide by 2 to get 1?
log2256 times.
- What do logarithms have to do with algorithms? (e.g., sorting)
- Consider an algorithm to search a data set of size n.
- Break up the data into two pieces (size n/2 each).
- Figure out (quickly) which piece has the data. ("quickly" means takes negligible time.)
- Continue the search with data set of size n/2.
- Repeat the procedure.
How long does this procedure take?
How many times can you recursively break up the data into two pieces?
Ans: log(n) times.
Thus, the procedure takes about log(n) steps (Eg. Binary search).
- Note: loge(x) is sometimes denoted lne(x)
Notes:
- If all instructions execute constant number of times (a small number that has no relationship with the input size), then the algorithm takes constant time ==> f(n) = O(1).
- When f(n)=log n, the big problem is transformed into a series of smaller problems, cutting the problem size by some constant fraction at each step. For example, binary search a sorted array.
- When f(n)=n (linear), a smaller amount of processing is done on each input element. (The code contains one loop).
- When f(n)=nlog n,
a large problem is broken into smaller subproblems, solving them independently, and then combining the solutions. Eg. Merge Sort.
- When f(n)=n2 (quadratic), all pairs of data items need to be processed (a nested loop with a depth of 2). Eg. Insertion Sort.
- When f(n)=2n (exponential), all input conbinations needs to be considered. The problem is hard. Eg. Many NP-Complete problems.
In-Class Exercise 1.8:
(Solution)
Use the definition of logarithms and the exponentiation rules to
show that: loga(xy) = loga(x) + loga(y).
- Useful sums:
- 1 + 2 + 3 + ... + n = n(n+1)/2
- 1 + a + a2 + a3 + ... + an
= (an+1 - 1) / (a - 1)
- 1 + a + a2 + a3 + ...
= 1/(a - 1) when 0 < a < 1 (infinite sum)
- 1 + 1/2 + 1/3 + 1/4 + ... + 1/n approx. equals logen
Simple timing of a Java program
Use the System.currentTimeMillis() method:
long startTime = System.currentTimeMillis();
// ... algorithm runs here ...
double timeTaken = System.currentTimeMillis() - startTime;
Famous algorithms
A brief mention of some "famous" algorithms and data structures:
- The Simplex algorithm:
- Used in linear programming, a class of optimization problems.
- Part of almost every optimization package.
- Needs some math background to understand.
- NOT an efficient algorithm (provably faster algorithms
exist), but "undefeated" until recently (by Karmarkar's algorithm).
- FFT:
- Fast Fourier Transform.
- Simple to implement, needs math background to understand.
- Used as a key building-block in just about every signal-processing software.
- Considered the "most used" algorithm of all time.
- Dijkstra's Shortest-Path algorithm:
- Currently the algorithm used for routing in the Internet.
- Simple to implement, using a binary heap.
- Interesting theoretical improvements exist.
- Since tens of thousands of internet routers run this algorithm every
few seconds, perhaps it should be considered the "most executed" algorithm.
- Quicksort:
- Exemplar of the "divide and conquer" technique.
- Easy to implement, hard to beat.
- Poor worst-case performance, excellent average-case performance.
- Hashing:
- Probably the "most used" data structure.
- Useful for "equality" search, sets.
- Except for pathological cases, extremely fast for insertion and retrieval.
- B-tree:
- Devised for accessing external files.
- Variations are used in almost every commercial database system.
- Simple, yet powerful.
- Block-oriented.
- Binary heap:
- Simple, efficient priority queue.
- Used in various graph algorithms.
- Efficient (and unusual) array implementation.
- Can be (but rarely) used for sorting.
- Splay tree:
- Self-balancing, self-adjusting binary tree.
- Less overhead than AVL-trees.
- Opened a new line of analysis: amortized analysis.
- Useful as both a "dictionary" and "priority-queue".
- Simulated Annealing:
- A simple algorithm, based on an interesting metaphor.
- Used for solving combinatorial problems.
- Not very efficient, but very easy to implement.
- The RSA algorithm:
- Named after Rivest-Shamir-Adleman.
- First public asymmetric public-key cryptographic algorithm.
- Easy to implement (but not as easy to implement efficiently).
- Not free - must pay authors royalty.
- Very popular, has made authors very rich.
- Effectiveness recently (2002) called into question by fast
primality testing.
In-Class Exercise 1.9:
Do a web search on "top ten algorithms".
(Solution)