- What exactly is stepwise refinement?
Answer: It is a process of programming, starting from an idea to finished, and refined, code. - When should I use stepwise refinement?
Answer: for most programming tasks!
This module has been written for the novice programmer who, quite understandably, has difficult getting started after reading a word description of a programming problem.
The main idea is to separate coding from problem-solving, and to proceed in small steps, even if the small steps seem like "a waste of time".
In this module, we will take up a programming problem and attack it using the stepwise approach. We will also look at the wrong way to attack the problem.
The Problem
In this problem, you are to move a chesspiece (a Knight) randomly around a chessboard and estimate how often it goes through the center of the chessboard. More precisely:
- If you don't know chess, that's OK. All you really need to know
is how a Knight moves on a chessboard:
- A chessboard is a 8 by 8 board of "cells" or "squares", alternately colored black and white, so that no two adjacent squares have the same color.
- Chess has several "pieces" each of which have their own moving characteristics.
- The Knight is one such piece. From its current position on the board, the Knight moves in an "L" shape: either (1) 2 squares in the vertical direction, and 1 in the horizontal direction, or (2) 1 square in the vertical direction, and 2 in the horizontal direction.
- For example, if we were to address the squares using standard
chess notation, the rows would be numbered 1,2,...,8 and the
columns would be labeled a,b,...,h. Then, a Knight at
location (c,4) has 8 possible places it could move to next:
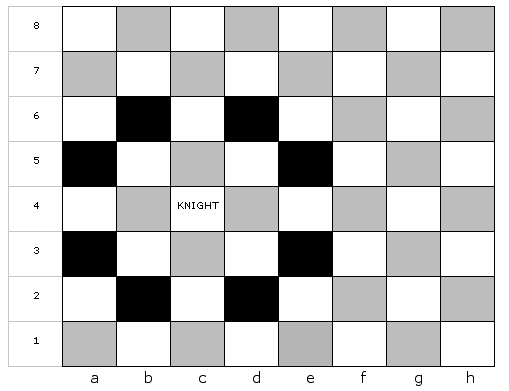
These eight places are: (a,3), (a,5), (b,2), (b,6), (d,2), (d,6), (e,3), (e,5) - Similarly, if the Knight were at location (a,1), it could only move to two possible places: (b,3) or (c,2).
- In this problem, we will initially place the Knight at location (a,1) - the bottom-left corner. Then, we will randomly pick a next location. So, when the Knight is at (a,1), we will pick randomly from (b,3) and (c,2). Let's say, we picked (c,2). Then, the Knight is moved to (c,2). Now, from (c,2), we identify next possible locations (there are 6), and pick one of them randomly. And so on.
- The goal is to move the Knight 1000 times, and count how many times the Knight lands in the center of the board. We will define the center of the board as the cells (d,4), (d,5), (e,4), (e,5).
- You are to estimate the fraction of time the Knight spends in the center in a 1000-move sequence. Do this by trying several simulation runs (each of 1000 moves), and averaging.
The Wrong Way
There is a temptation with the novice programmer to start coding as soon as possible. For example, the following steps, while apparently reasonable, eventually will create problems:
- "Let see...I'll need a 2D array to store the chessboard, so let
me start by defining that..."
public class Knight { public static void main (String[] argv) { int[][] board; } } - "OK, now I'll look up how the professor created a 2D array, and
use that sort of code..."
public class Knight { public static void main (String[] argv) { int[][] board; board = new int[8][]; for (int i=0; i < 8; i++) board[i] = new int[8]; // Initialize for (int i=0; i < 8; i++) for (int j=0; j < 8; j++) board[i][j] = 0; } } - "Great, now let me place the Knight at the bottom corner..."
public class Knight { public static void main (String[] argv) { int[][] board; board = new int[8][]; for (int i=0; i < 8; i++) board[i] = new int[8]; // Initialize for (int i=0; i < 8; i++) for (int j=0; j < 8; j++) board[i][j] = 0; // Place Knight at (0,0) board[0][0] = 1; } } - "Now, let me figure out how to move the Knight..."
This approach to a programming problem is, to put it bluntly, weak!
Like any other complex activity, a little thought and planning go a long way.
Stepwise Refinement
The key principles in Stepwise Refinement:
- Separate problem-solving from coding.
- Perform coding only after you have completed most of
problem-solving.
Note: for extremely large projects, this may not be true, since you may break your project into smaller pieces, and solve them separately. But for each piece, you should code only after problem-solving. - Use pen and paper to scratch out your broad approach, and then refine this as you go along.
- Write in debugging statements while you code, NOT after coding.
In the sequel, we will take our problem and apply the Stepwise Refinement procedure.
Step 1: Put your arms around the problem
First, let's make sure we understand the problem:
- Do we need to understand more about chess to solve the problem?
Answer: No, but if you're curious it won't hurt to spend a few minutes on the web, or watch someone play chess. - Is the problem completely specified?
Answer: How do we know this? One way to approach this, is to simulate the problem by hand. Draw a chessboard (or borrow an actual chessboard) and try out the problem:- Start with the Knight in the bottom left corner.
- Where can it move? Then, pick one of these locations randomly.
- Next, identify where it can move next, etc.
- What is the desired output? Can we produce the output with our
manual simulation?
- We need to move the Knight 1000 times (OK, we can do that in our manual simulation), and count how often the Knight lands in one of the center squares (Yes, that's also do-able).
- What about this "estimate the fraction" stuff? Well,
in a particular manual trial, we might land in the center 400
times of the 1000 moves. What if the random numbers were
different? In another trial, it might have been 300 times.
Our goal should be: repeat this experiment (1000 moves per experiment) many times; each time, obtain the fraction (e.g., 400/1000); then, take the average over all these trials. - OK, so how many trials should we use? The problem description doesn't specify. At this point, we could request clarification, or use a large enough number like 10,000 or 100,000.
So, in theory, we now understand the problem well enough that we can manually produce the output if we had to.
Things NOT to do at this time:
- Don't think about coding or even data structures yet.
- Don't even think about your solution approach (yet!).
Step 2: Outline the broad approach on paper
Now is the right time to set up the broad overall approach to the problem:
- At this time, we are not going to worry about code, just overall approach.
- Use paper, and scratch out only a broad outline of the steps, where each step doesn't have much detail.
For example, here's what I wrote down:
1. Repeat this 10,000 times:
1.1 Start with Knight at (0,0).
1.2 Move it 1000 moves, and record how many moves
landed in the center.
1.3 Compute the fraction for this run.
2. Compute the average over the 10,000 runs.
3. Print results.
Some things to observe:
- There's no hint of coding yet. Indeed, this is simply a "recipe" outline for getting the job done.
- The key elements are in place: (1) the fact that we are repeating an experiment many times (10,000 times); (2) the fact that each experiment is itself a complicated thing (Moving a Knight 1000 moves).
- Computational details are left out (like, how to compute an average).
- Although we have hard-coded a number like 10,000 (for clarity), later we know we can use a variable.
- A language-independent outline like the above is sometimes called pseudo-code.
Next, review the outline and check to make sure it really is going
to work! For example, here's an outline that does NOT work:
1. Repeat this 10,000 times:
1.1 Start with Knight at (0,0).
1.2 Move it 1000 moves, and record how many moves
landed in the center.
1.3 Compute the fraction for this run.
1.4 Compute the average.
2. Print results
Exercise s.1: Why doesn't this work?
What NOT to do at this stage:
- Avoid any language-dependent statements at this stage.
- Try to avoid computation detail, and instead create the overall structure.
- Don't think about code, or methods, or anything like that.
Step 2: Put the broad outline into comments in a program
Next, we are going to write a program "shell" and put down the
pseudocode inside the shell, as comments:
public class KnightSolution {
public static void main (String[] argv)
{
// 1. Repeat this 10,000 times
// 1.1 Start with Knight at (0,0).
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
// 1.3 Compute the fraction for this run.
// 2. Compute the average over 10,000 runs.
// 3. Print results
}
}
At this point, we don't really need to compile, but it doesn't hurt to compile either.
Step 3: Put in some detail working from the outside in
Next, we are going to put in some detail:
public class KnightSolution {
public static void main (String[] argv)
{
int numRuns = 10000;
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Observe:
- We have only addressed the outer "estimation" process.
- Although we have declared and used a couple of variables, we have not addressed how frac is determined.
- Note that the basic estimation process is in place: run an experiment numRuns times, and take the average. This outer shell would work for any experiment in which we are trying to observe a quantity or property.
- Our documentation has already begun: the comments document the structure.
What NOT to do at this time:
- Don't try to solve the smaller details about moving the Knight yet.
- Don't think about data structures (such as representing the board etc) just yet.
Step 4: Take a first cut at data structures
Exercise s.2: Before reading ahead, outline what data structures might be useful.
Now, let's look at the broad outline and ask ourselves what data structures would be useful:
- How should we track the Knight's moves?
- Is it enough to just store the current position in two int's?
int x, y; - Or should we keep a grid (2D array) to record the current position?
- Is it enough to just store the current position in two int's?
- How about printing debugging information? Should we print out a chessboard (and therefore record the chessboard in a data structure)?
- Where should we count the number of times the Knight lands in the center?
Now, we DO NOT have to get this right the first time. If our data structures are too big, or too inefficient, that's OK for a first cut.
So, let's take the following approach:
- We will keep a "picture" of the current state of the
chessboard:
- An obvious data structure is a 2D array:
int[][] board; - We can use a 1 in the right cell to identify the current location for the knight and set other locations to 0.
- Thus, if printed out, the board would look like this, for example:
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0Here, the knight is at location (2,2) (viewed upside down, but that's alright for now).
- An obvious data structure is a 2D array:
- One finer point about the chessboard: where should it be
created?
- Since the size of the chessboard is not changing, we can create it outside the run loop (just once).
- Of course, we need to re-initialize it for every run.
- Let's use int variables to keep track of the current
position of the knight.
int x, y;
So, at this point:
public class KnightSolution {
static int[][] board;
public static void main (String[] argv)
{
int numRuns = 10000;
// Create chessboard.
board = new int[8][];
for (int i=0; i < 8; i++) {
board[i] = new int[8];
}
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
// Initialize board here.
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
board[i][j] = 0;
}
}
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Finally, we can clean up the code a little by moving some code
into methods:
public class KnightSolution {
static int[][] board;
// Create the space for the board.
static void createBoard ()
{
board = new int[8][];
for (int i=0; i < 8; i++) {
board[i] = new int[8];
}
}
// Set all board entries to 0.
static void cleanBoard ()
{
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
board[i][j] = 0;
}
}
}
public static void main (String[] argv)
{
int numRuns = 10000;
// Create chessboard.
createBoard ();
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
cleanBoard ();
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Exercise s.3: Before reading ahead, flesh out some pseudocode for the inner loop (1.3 and 1.4).
Step 5: Fill out pseudocode for lower level of detail
At this point, we are going to fill in some detail in the inner
loop:
Since there is significant logic inside, we will first
write pseudocode:
public class KnightSolution {
static int[][] board;
// Create the space for the board.
static void createBoard ()
{
board = new int[8][];
for (int i=0; i < 8; i++) {
board[i] = new int[8];
}
}
// Set all board entries to 0.
static void cleanBoard ()
{
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
board[i][j] = 0;
}
}
}
public static void main (String[] argv)
{
int numRuns = 10000;
// Create chessboard.
createBoard ();
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
cleanBoard ();
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
for (int move=1; move<=1000; move++) {
// Identify possible next locations.
// Pick one of them randomly.
// Set x,y to new locations.
// If new location is a center location, update count.
}
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Observe:
- We created a for loop for the moves. Right now, we've hardcoded 1000 moves, but later we should change that to a variable.
- Inside the loop, we ONLY have pseudocode, at this time.
- Following our stepwise refinement procedure, we will address data structures for the inner loop FIRST, and THEN look into coding details.
Step 6: Data structures for next level of detail
Once again, let's take a look at the key steps in the inner loop:
for (int move=1; move<=1000; move++) {
// Identify possible next locations.
// Pick one of them randomly.
// Set x,y to new locations.
// If new location is a center location, update count.
}
Exercise s.4: Before reading ahead, outline what data structures might be useful for this inner loop.
What data structures are we going to need for this part?
- Since there are 8 possible next locations (at most), we could use a data structure to hold the 8 locations.
- Once we "hold" the locations, we will be able to select randomly from amongst them.
- What about the "count"?
- One option is to create a 2D array to hold the count for
each square:
int[][] count; ... // if Knight lands in x,y then update count count[x][y] ++;This way, we will get the "count" for the 4 center squares:centerCount = count[3][3] + count[3][4] + count[4][3] + count[4][4]); - But do we really need to track the "counts" for other squares?
- One option is to create a 2D array to hold the count for
each square:
Let's take this approach:
- Arrays to hold the 8 locations:
int[] possibleX = new int[8]; int[] possibleY = new int[8]; - Where is this created?
Clearly, the size never changes, so we can do this just once. - No 2D count array.
Step 7: Problem-solving at the next level of detail
OK, now we can start attacking the details of the inner loop:
- Computing next possible locations:
- Suppose the current location is (x,y).
- Then, the 8 potential locations are:
- (x+2, y+1)
- (x+2, y-1)
- (x-2, y+1)
- (x-2, y-1)
- (x+1, y+2)
- (x+1, y-2)
- (x-1, y+2)
- (x-1, y-2)
- Of these, some will be "off board" and will have to be rejected.
- Let's put down some rough pseudocode to put these in the array:
// Check each possible next location from the 8. // For each one of them, see if the location is "on board" // To check if it's on board, make sure x,y values are in the range 0-7
- How do we pick a next location randomly?
- Suppose the number of locations is in the variable numLocations.
- We can draw a random number between 1 and
numLocations:
whichLocation = UniformRandom.uniform (0, numLocations-1);
Let's write methods for each of these small tasks:
- A method to check the validity of a location:
static boolean validLocation (int x, int y) { // Check if x value is out of range. if ( (x < 0) || (x > 7) ) return false; // Check if y value is out of range. if ( (y < 0) || (y > 7) ) return false; // Otherwise, it's OK. return true; } - A method to generate possible locations:
// Create possible locations and return number of such locations. // The input location is x,y static int identifyPossibleLocations (int x, int y) { // Check the different possibilities (x+2, y+1) etc. int numLocations = 0; // Check first one. if (validLocation (x+2, y+1)) { // Put this in the array. possibleX[numLocations] = x+2; possibleY[numLocations] = y+1; numLocations ++; } // Next: if (validLocation (x+2, y-1)) { // Put this in the array. possibleX[numLocations] = x+2; possibleY[numLocations] = y-1; numLocations ++; } // Others: 3 if (validLocation (x-2, y+1)) { // Put this in the array. possibleX[numLocations] = x-2; possibleY[numLocations] = y+1; numLocations ++; } if (validLocation (x-2, y-1)) { // 4 possibleX[numLocations] = x-2; possibleY[numLocations] = y-1; numLocations ++; } if (validLocation (x+1, y+2)) { // 5 possibleX[numLocations] = x+1; possibleY[numLocations] = y+2; numLocations ++; } if (validLocation (x+1, y-2)) { // 6 possibleX[numLocations] = x+1; possibleY[numLocations] = y-2; numLocations ++; } if (validLocation (x-1, y+2)) { // 7 possibleX[numLocations] = x-1; possibleY[numLocations] = y+2; numLocations ++; } if (validLocation (x-1, y-2)) { // 8 possibleX[numLocations] = x-1; possibleY[numLocations] = y-2; numLocations ++; } return numLocations; }
Now, let's put all of this together:
public class KnightSolution {
static int[][] board;
static int[] possibleX = new int[8];
static int[] possibleY = new int[8];
// Create the space for the board.
static void createBoard ()
{
board = new int[8][];
for (int i=0; i < 8; i++) {
board[i] = new int[8];
}
}
// Set all board entries to 0.
static void cleanBoard ()
{
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
board[i][j] = 0;
}
}
}
static boolean validLocation (int x, int y)
{
// Check if x value is out of range.
if ( (x < 0) || (x > 7) )
return false;
// Check if y value is out of range.
if ( (y < 0) || (y > 7) )
return false;
// Otherwise, it's OK.
return true;
}
// Create possible locations and return number of such locations.
// The input location is x,y
static int identifyPossibleLocations (int x, int y)
{
// Check the different possibilities (x+2, y+1) etc.
int numLocations = 0;
// Check first one.
if (validLocation (x+2, y+1)) {
// Put this in the array.
possibleX[numLocations] = x+2;
possibleY[numLocations] = y+1;
numLocations ++;
}
// Next:
if (validLocation (x+2, y-1)) {
// Put this in the array.
possibleX[numLocations] = x+2;
possibleY[numLocations] = y-1;
numLocations ++;
}
// Others: 3
if (validLocation (x-2, y+1)) {
// Put this in the array.
possibleX[numLocations] = x-2;
possibleY[numLocations] = y+1;
numLocations ++;
}
if (validLocation (x-2, y-1)) { // 4
possibleX[numLocations] = x-2;
possibleY[numLocations] = y-1;
numLocations ++;
}
if (validLocation (x+1, y+2)) { // 5
possibleX[numLocations] = x+1;
possibleY[numLocations] = y+2;
numLocations ++;
}
if (validLocation (x+1, y-2)) { // 6
possibleX[numLocations] = x+1;
possibleY[numLocations] = y-2;
numLocations ++;
}
if (validLocation (x-1, y+2)) { // 7
possibleX[numLocations] = x-1;
possibleY[numLocations] = y+2;
numLocations ++;
}
if (validLocation (x-1, y-2)) { // 8
possibleX[numLocations] = x-1;
possibleY[numLocations] = y-2;
numLocations ++;
}
return numLocations;
}
public static void main (String[] argv)
{
int numRuns = 10000;
// Create chessboard.
createBoard ();
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
cleanBoard ();
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
int centerCount = 0;
for (int move=1; move<=1000; move++) {
// Identify possible next locations.
int numLocations = identifyPossibleLocations (x, y);
// Pick one of them randomly.
int nextLocation = (int) UniformRandom.uniform ((long) 0, (long) numLocations);
// At this time, possibleX[] and possibleY[] contain the possible locations.
// Set x,y to new locations.
x = possibleX[nextLocation];
y = possibleY[nextLocation];
// If new location is a center location, update count.
if ( ( (x==3) && (y==3) )
|| ( (x==3) && (y==4) )
|| ( (x==4) && (y==3) )
|| ( (x==4) && (y==4) ) ) {
centerCount ++;
}
// Update fraction.
frac = (double) centerCount / (double) 1000;
}
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Step 8: Review
At this point, we have most of our code. This is a good time to look over the code to see if we've missed anything, or can improve anything:
- We have left out the documentation at the top of the file.
- The variables at the top are not documented.
- We might move the "center-checking" to a method.
- We've hardcoded the number of moves to 1000 - we could use a variable instead.
OK, let's make these changes:
/**
* KnightSolution is a static class that is used to compute the
* probability that a randomly moving chesspiece (a Knight) lands
* in the center. The approach taken has the following outline:
* 1. Repeat this 10,000 times:
* 1.1 Start with Knight at (0,0).
* 1.2 Move it 1000 moves, and record how many moves
* landed in the center.
* 1.3 Compute the fraction for this run.
* 2. Compute the average.
* 3. Print results
*
* @author Rahul Simha
*
*/
public class KnightSolution {
// Representation of board with Knight:
// board[i][j] == 1 if the Knight is at (i,j);
// board[i][j] == 0 otherwise.
static int[][] board;
// Possible locations are stored here.
// The i-th possible location has coordinates
// (possibleX[i], possibleY[j])
static int[] possibleX = new int[8];
static int[] possibleY = new int[8];
// Create the space for the board.
static void createBoard ()
{
board = new int[8][];
for (int i=0; i < 8; i++) {
board[i] = new int[8];
}
}
// Set all board entries to 0.
static void cleanBoard ()
{
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
board[i][j] = 0;
}
}
}
static boolean validLocation (int x, int y)
{
// Check if x value is out of range.
if ( (x < 0) || (x > 7) )
return false;
// Check if y value is out of range.
if ( (y < 0) || (y > 7) )
return false;
// Otherwise, it's OK.
return true;
}
// Create possible locations and return number of such locations.
// The input location is x,y
static int identifyPossibleLocations (int x, int y)
{
// Check the different possibilities (x+2, y+1) etc.
int numLocations = 0;
// Check first one.
if (validLocation (x+2, y+1)) {
// Put this in the array.
possibleX[numLocations] = x+2;
possibleY[numLocations] = y+1;
numLocations ++;
}
// Next:
if (validLocation (x+2, y-1)) {
// Put this in the array.
possibleX[numLocations] = x+2;
possibleY[numLocations] = y-1;
numLocations ++;
}
// Others: 3
if (validLocation (x-2, y+1)) {
// Put this in the array.
possibleX[numLocations] = x-2;
possibleY[numLocations] = y+1;
numLocations ++;
}
if (validLocation (x-2, y-1)) { // 4
possibleX[numLocations] = x-2;
possibleY[numLocations] = y-1;
numLocations ++;
}
if (validLocation (x+1, y+2)) { // 5
possibleX[numLocations] = x+1;
possibleY[numLocations] = y+2;
numLocations ++;
}
if (validLocation (x+1, y-2)) { // 6
possibleX[numLocations] = x+1;
possibleY[numLocations] = y-2;
numLocations ++;
}
if (validLocation (x-1, y+2)) { // 7
possibleX[numLocations] = x-1;
possibleY[numLocations] = y+2;
numLocations ++;
}
if (validLocation (x-1, y-2)) { // 8
possibleX[numLocations] = x-1;
possibleY[numLocations] = y-2;
numLocations ++;
}
return numLocations;
}
public static void main (String[] argv)
{
int numRuns = 10000;
int numMoves = 1000;
// Create chessboard.
createBoard ();
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
double frac = 0;
// 1.1 Start with Knight at (0,0).
cleanBoard ();
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
int centerCount = 0;
for (int move=1; move<=numMoves; move++) {
// Identify possible next locations.
int numLocations = identifyPossibleLocations (x, y);
// Pick one of them randomly.
int nextLocation = (int) UniformRandom.uniform ((long) 0, (long) numLocations);
// At this time, possibleX[] and possibleY[] contain the possible locations.
// Set x,y to new locations.
x = possibleX[nextLocation];
y = possibleY[nextLocation];
// If new location is a center location, update count.
if ( ( (x==3) && (y==3) )
|| ( (x==3) && (y==4) )
|| ( (x==4) && (y==3) )
|| ( (x==4) && (y==4) ) ) {
centerCount ++;
}
// Update fraction.
frac = (double) centerCount / (double) 1000;
}
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Step 9: Testing and Debugging
The wrong next step is to assume the program works.
(In fact, there is a bug in the program.)
Instead, we should build debugging output before executing the program:
- This is probably the most useful tip in problem-solving.
- It will help to print out, for each Knight move:
- The status of the board.
- The current location of the Knight.
- The possible next locations.
- Initially, we will do a debugging run for only a few moves (10), and ONE run.
Here is a "debug"-ready version of the program:
public class KnightSolution {
static boolean debug = true;
// Representation of board with Knight:
// board[i][j] == 1 if the Knight is at (i,j);
// board[i][j] == 0 otherwise.
static int[][] board;
// Possible locations are stored here.
// The i-th possible location has coordinates
// (possibleX[i], possibleY[j])
static int[] possibleX = new int[8];
static int[] possibleY = new int[8];
// Create the space for the board.
static void createBoard ()
{
// ...
}
// Set all board entries to 0.
static void cleanBoard ()
{
// ...
}
static boolean validLocation (int x, int y)
{
// ...
}
// Create possible locations and return number of such locations.
// The input location is x,y
static int identifyPossibleLocations (int x, int y)
{
// ...
}
// New method to help with debugging.
static void printPossibleLocations (int numLocations)
{
System.out.print ("Possible Locations: ");
for (int i=0; i < numLocations; i++)
System.out.print (" (" + possibleX[i] + "," + possibleY[i] + ")");
System.out.println ();
}
// New method to help with debugging.
static void printBoard ()
{
System.out.println ("Board status: ");
for (int i=0; i < 8; i++) {
for (int j=0; j < 8; j++) {
System.out.print (" " + board[i][j]);
}
System.out.println ();
}
}
public static void main (String[] argv)
{
int numRuns = 1;
int numMoves = 10;
// Create chessboard.
createBoard ();
// 1. Repeat this 10,000 times
double totalFrac = 0;
for (int run=1; run<=numRuns; run++) {
// NOTE: debug flag
if (debug)
System.out.println ("Run# " + run);
double frac = 0;
// 1.1 Start with Knight at (0,0).
cleanBoard ();
// Put the knight in location (0,0).
board[0][0] = 1;
// Current location of knight.
int x=0, y=0;
// 1.2 Move it 1000 moves, and record how many moves
// landed in the center.
int centerCount = 0;
for (int move=1; move<=numMoves; move++) {
// Identify possible next locations.
int numLocations = identifyPossibleLocations (x, y);
// Pick one of them randomly.
int nextLocation = (int) UniformRandom.uniform ((long) 0, (long) numLocations);
// Debug.
if (debug) {
System.out.println (">> Move# " + move + " cur_x=" + x + " cur_y=" + y +
" numLoc=" + numLocations + " nextLoc=" + nextLocation);
printPossibleLocations (numLocations);
printBoard ();
}
// At this time, possibleX[] and possibleY[] contain the possible locations.
// Set x,y to new locations.
x = possibleX[nextLocation];
y = possibleY[nextLocation];
// If new location is a center location, update count.
if ( ( (x==3) && (y==3) )
|| ( (x==3) && (y==4) )
|| ( (x==4) && (y==3) )
|| ( (x==4) && (y==4) ) ) {
centerCount ++;
}
// Update fraction.
frac = (double) centerCount / (double) 1000;
}
// 1.3 Compute the fraction for this run.
totalFrac = totalFrac + frac;
}
// 2. Compute the average.
double fracEstimate = totalFrac / numRuns;
// 3. Print results
System.out.println ("Estimate: " + fracEstimate);
}
}
Exercise s.5: Can you find the bug?