Assignment 1

Objectives and example

The goals of this assignment:

Practice with 2D arrays.
Using array lists.
An open-ended project that encourages creativity.

As usual, we'll start by working together on a slightly harder problem than the ones you will do by yourself.

Consider this problem: we are given a 2D array of numbers, from which we are to compute a second 2D array of numbers (same size 2D array) in the following way: every element in the second array is the average of the values in the neighboring cells in the original array. A picture will explain this better:

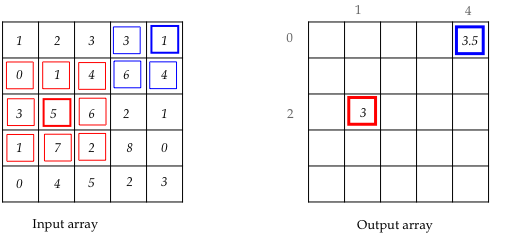
Let's call the input array A and the output array B. Consider the red element on the right, which is B[2][1]. To compute the element B[2][1], look at A[2][1] and the nine neighboring cells, all shown in red in the A array. We will include the cell A[2][1] itself in the set of neighbors. The value to be assigned to B[2][1] is the average of these nine values: (0 + 1 + 4 + 3 + 5 + 6 + 1 + 7 + 2) / 9, which turns out to be 4.

In some cases, cells have fewer than nine neighbors, like the blue cell A[0][4] shown, which has a four-cell neighborhood. Thus, the average to be stored in B[0][4] is: (3 + 1 + 6 + 4) / 4 = 3.5.

A1.1 Exercise: At this point do not write any code. Try to sketch out a solution in pseudocode. See how far you get before reading through the solution.

Now work through the solution

And now, on to your assignment. Good luck!

Assignment problems

In this problem, in CheckChessBoard.java. you will write a method that checks whether an integer 2D array consisting entirely of 0's and 1's is patterned on a chessboard. Call the method
```
    public static boolean isValidChessBoard (int[][] board)
    {
         // Returns true or false, depending on whether the array
         // satisfies certain properties.
    }
     
```
Although the standard chessboard is 8×8, we will allow any N×N as long as N>3. Here's an example:
```
	int[][] A = {
	    {0,1,0,1},
	    {1,0,1,0},
	    {0,1,0,1},
	    {1,0,1,0}
	};
     
```
The basic properties to be satisfied are:
- It must be a square.
- The only values allowed are 0 and 1.
- Every cell's vertical and horizontal neighbors must of the opposite kind.
- The diagonal neighbors must be of the same kind.
Download TestChessBoard.java and use it for testing your program. Note: a smart thing to do while testing is to comment out all but one test and get your program working test-by-test.
In the days of yore, long before smartphones, people on travel would entertain themselves with word puzzles. One popular word puzzle of those times was to use a letters of a given to see how many other words you can make. For example, from the word "conserve", you can use its letters to form three-letter words like "con" or "ore", or five-letter words like "serve". There are games like TextTwist that are similar.
In this exercise, we'll use a slight variation. You will take as input a word and print all the valid three-letter words one can make with its letters, but where the letters of the three-letter word occur in the order as in the original word. Thus, from "conserve", the three letter word "one" is acceptable because the occur in order:
```
  conserve     
     
```
But the three letter word "son" is not acceptable because those letters do not occur in the order they exist in "conserve".
Call your method
```
     public static int threeLetterFinder (String inputWord)
     {
	  ArrayList<String> words = WordTool.getUnixWordsAsList ();

          // Uses the letters of inputWord form all possible valid
          // three-letter words that occur in sequence. Define valid
          // as: it must be in the list of unix words above.
          // Also: print the total number of 3-letter in-sequence combinations.
     }
     
```
And write your program in ThreeLetterFinder.java. Thus, the output for "conserve" should be:
```
8 three-letter subwords for 'conserve' out of 56 possible combinations
 >> con
 >> cos
 >> one
 >> ore
 >> nee
 >> see
 >> ere
 >> eve
     
```
You will also need WordTool.java and words.txt
From amongst all the English words in the unix collection above, which word has the largest number of three-letter in-sequence subwords? Write a program (in ThreeLetterFinder2.java) to determine this word and list its in-sequence three-letter subwords.
Art Project, part II. In the examples on Brownian motion and modeling the spread of infection, we saw how to use animation in DrawTool. The basic idea is:
```
	DrawTool.startAnimationMode ();

        for ( ... ) {
  
            // Draw a scene slightly different from the 
            // scene in the previous iteration

	    DrawTool.animationPause (100);
        }

	DrawTool.endAnimationMode ();
     
```
What makes it an animation is that the objects on the drawing should be moved only slightly, to create the effect of motion.
Many modules ago, you used DrawTool for your first art project with programming. Now, knowing all that you know, it should be possible to create a more sophisticated art project with animation, with multiple types of objects, with some "interacting physics" between the objects, and other ideas. The goal of this part of the assignment is to do exactly that: end the course with a visually arresting, animated art project. Write your code in MyFinalArtProject.java.
For the reading and exploration part, we'll focus on two items:
1. Looking back. We've seen a picture of the ENIAC. Read about the history of the ENIAC and one other first-generation computers. Write a couple of paragraphs on the early history.
2. Looking forward. Pick any field from the arts and humanities, and imagine an application of computer science. Explain why your application would be of interest and why you think it's both futuristic (it should certainly not exist today) and why it's feasible.
Write your responses in assignment1.pdf.

A1.0 Audio: