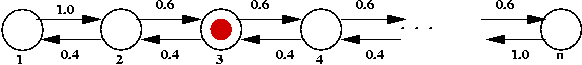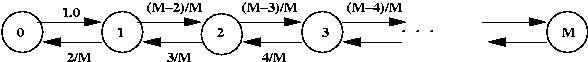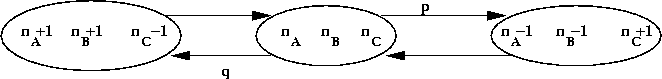Simulation: An Introduction

Overview of Computation in Biology

Search problems

Data characterization problems
Visualization:
Special purpose algorithms:
Simulation: (this lecture)

What is Simulation?

Broad definition: A simulation is a computational model of a "process".

More specific definition:

Example:

Characteristics of a simulation:
Types of simulation:

Exercise: Find two examples of biology-related simulation on the web. See if you can categorize them into "continuous" or "discrete".

Anatomy of a Discrete-Event Simulation: Random Walk Example

Demo: 1-D random walk
General structure of 1-D random walk:

  • Collection of "states" ordered left to right:

    Here, the states are numbered 1, ..., n

  • Think of a "token" that represents the current state:

  • At each state, there are "jump probabilities" specifying motion of the token to the left or right.

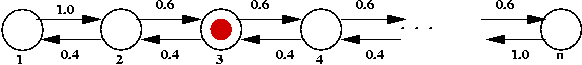
    Thus, in this example, there's a propensity to drift rightwards.

  • The token starts in some state and at each step jumps randomly (according to jump probabilities) to a neighboring state.

  • Let Xk = state after k jumps.

  • Typical questions of interest:
    • What is Pr[Xk = i]?
    • What is limk -> infinity Pr[Xk = i]?
    • What is E[Xk]?

Why study random walks?

Types of random walks:

  • Reflecting random walks:

  • Absorbing random walks:

    Example: gambler's ruin problem

    Question of interest: what is Pr[gambler is ruined]?

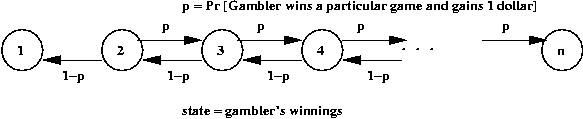
Simulating a random walk:

  • Suppose we want to estimate Pr[gambler is ruined]? above.

  • Simulation parameters:
    • p = 0.4
    • Start with fortune = n/2.

  • First, consider simulating a single walk: 
    Algorithm: gamblerRuin (N)
Input: the highest state
1.  state = N/2
2.  reachedZero = false
3.  reachedN = false

4.  while not (reachedZero or reachedN)
5.    if coinFlip(0.4) 
6.      state = state + 1     // Go to state + 1
7.    else               
8.      state = state - 1     // Go to state - 1
9.    endif

10.   // See if game is over.
11.   if state == 0 
12.     reachedZero = true
13.   if state == N
14.     reachedN = true
15. endwhile

16. return reachedZero

Output: whether random walk was absorbed at the left

  • Now, to get a proper estimate we'll have to repeat this several times: 
    Algorithm: estimateRuin (N)

1.   numRuins = 0
2.   for i=1 to numTrials
3.     ruined = gamblerRuin (N)
4.     if ruined
5.       numRuins = numRuins + 1
6.     endif
7.   endfor
8.   return numRuins / numTrials

Simulation Example: Epidemiology

Epidemiological questions of interest:

  • What is the rate of infection (new infections/day)?

  • What percent of population gets infected?

  • How effective are vaccination policies? e.g.,
    • Flu: vaccinate school kids, medical workers
    • Smallpox: vaccinate medical/rescue workers, police, military

Modeling approaches:

  • Differential equations:
    • Write down a differential equation that expresses key characteristics of system.
    • Solve analytically or numerically.

  • Simulation:
    • Build detailed computational model.
    • Implement simulation.
    • Run simulations to extract statistics.

Differential-equation modeling of epidemics:

  • Consider a population of size N.

  • Let U(t) = number of uninfected people.

  • Let I(t) = number of infected people.

  • Modeling assumption: the rate of new infections depends on:
    • I(t)
      => the higher I(t), the more the chance of infectious contact
    • U(t)
      => the higher U(t), the higher the number of susceptible people.
    • Thus, [I(t+s) - I(t)] / s = (constant) U(t) I(t).
    • Alternatively: [U(t+s) - U(t)] / s = - (constant) U(t) I(t).

  • Differential equation: U'(t) = - b U(t)I(t).

  • Turns out: can be solved analytically in some cases.

Advantages of differential-equation modeling:

  • Well-known solution techniques (over 300 years of mathematics).

  • Easily verifiable (mathematical proofs).

  • Forces attention on key characteristics.

  • Analytic solutions provide insight (e.g., exponential growth vs. linear growth).

Limitations of differential-equation modeling:

  • Only simple cases are tractable.

  • It's hard, if not impossible, to model:
    • Randomness, e.g., probabilistic contact
    • Individual behavior, e.g., individuals that use history of observed behavior
    • Non-linear effects, e.g., vaccination policies
    • Spatial effects, e.g., contact in spatial vicinity

A simple simulation model:

  • "Agents" (people) roam about randomly on a 2D grid (modeling contact).

  • Infections occur between an uninfected agent and infected agent in the same cell (spatial effects).

  • Goal: estimate number of infected agents at end of simulation.

Demo

A more complex simulation model:

  • Agent characteristics:
    • Families with different sizes.
    • Age distributions and age-based susceptibility.

  • Spatial characteristics:
    • Contact in workplaces, schools, malls, hospitals.
    • Randomness in time spent, number of contacts.

  • Disease characteristics:
    • Injection model: how does it start?
    • Progression parameters: incubation, immunity, contagiousness, susceptibility.
    • Infection events: workplace events, age-based, school-based.

  • Policy characteristics:
    • Vaccination policies: forced vaccination, inducements, school-based.
    • Information distribution: monitoring, health-alerts.

Demo (work in progress)

Simulation Example: Protein Folding

Protein folding overview:

  • Why: protein folds = protein function

  • Estimate: about 3000 different types of folds
    => currently 300 folds in PDB

  • Computational goal: given protein sequence, predict folds

  • Note: a single protein can have multiple domains, each with its own important fold/function.

One computational approach:

  • Model force/energy interactions at atomic or small-molecule level.

  • Each configuration (fold) has an associated (potential) energy.

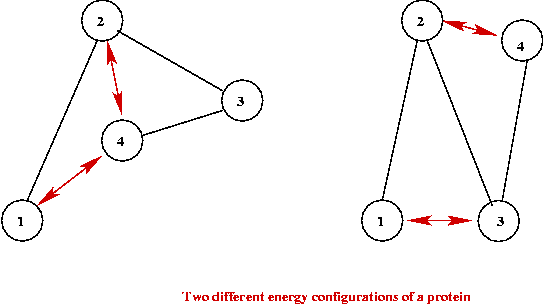
  • Computational goal: find minimal energy configuration.

An illustrative example: 2D protein folding:

  • Use 2D grid to represent space.

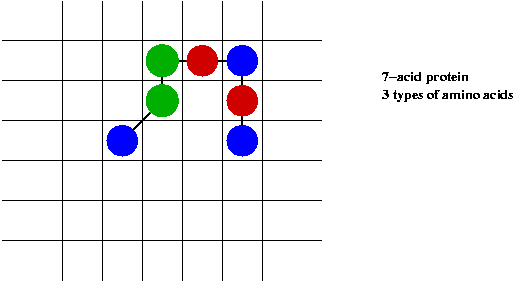
    • Each amino acid occupies one cell.
    • Interaction between neighboring cells.
    • Protein must occupy contiguous cells.

  • Energy computation:

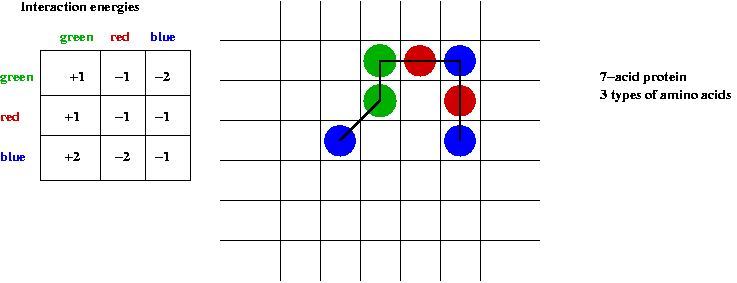
    • Specify amino-amino energies in a table.
    • Total energy = sum of all neighboring amino-amino energies.

Exercise: Compute the energy of the above fold.

  • Solution procedure:
    • Start with a random guess (fold).
    • Modify fold to see whether a "better" fold can be found.
    • Iterate until low-energy configuration is found.

Demo

Why it's a hard computational problem:

  • Iterative folding gets "stuck" at local minima.
  • Astronomically large number of possible folds.

Solution approaches:

Membrane Simulation

Membrane simulation goals:

  • Modeling of membrane structure and formation.
  • Modeling of transport through membranes.
  • Modeling of membrane protein interactions.

Why membranes?

  • Lot of molecular chemistry (signalling etc) occurs at membranes.
  • Estimate: 30% of proteins involved in some membrane function.
  • Common target for drugs.
Demo: simple membrane formation model (compare)

Simulating Chemistry

Differential equation models:

  • Consider a chemical A that transforms into B:

  • The rate at which A transforms into B depends on the number of A molecules:
    dB/dt = k A

  • Similarly, dA/dt = -k B
    (because A + B = constant)

  • For a reaction A + B <=> C, the equations are
    • dC/dt = k AB
    • dA/dt = - k AB
    • dB/dt = - k AB

  • Solve using standard diff-eq methods or packages.

  • Solution: equilibrium quantities.

Stochastic models:

  • Consider the reaction A + B <=> C.

  • Let
    nA = number of A molecules
    nB = number of B molecules
    nC = number of C molecules

  • At any time, the current "state" of the system is given by (nA, nB, nC)

  • Define state transition probabilities:

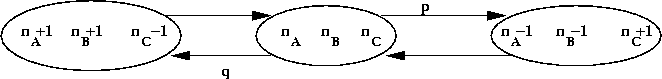
  • Here, p and q may depend on the state.

  • To solve: run simulation and compute statistics.

  • Possible to extract chemical dynamics from simulation.

Modeling catalysis

  • Consider the following reaction:

  • We can model the reaction as follows:
    • At each step (e.g., a nanosecond), the forward reaction is:
      A = A - x
      B = B - x
      C = C + 2x
    • Here, x is a small quantity (fixed number of molecules).
    • Reaction proceeds only if ABD > threshold.

Simulation and Origin-of-Life Theories

Let's start with some perspective:
Event How many years ago
Big bang 20,000,000,000
Planets 5,000,000,000
Life 3,500,000,000?
Photosynthesis 2,500,000,000
First eukaryote 1,500,000,000
Multicellular 1,000,000,000
Modern man 200,000
? ?
Beginning of semester 0.25
Beginning of lecture 0.000171

Exercise: Fill in the question marks in the above table with something interesting that's related to biology.

Current favorite theory:

  • Early earth (post big-bang) had no organic compounds.
  • Bombardment by cosmic rays, lightning, UV etc created simple organic compounds.
    => the "primitive soup"
  • Primitive soup contained amino acids, nucleic acids.
  • RNA happens!
  • Then came DNA, Krebs cycle, protein machinery etc.

But ...

  • Which came first: proteins or nucleic acids?
    • Proteins first theory: nucleic-acid structures were facilitated by proteins.
    • Naked genes theory: DNA first replicated by itself, proteins were created later.

  • What are the chances that a complex molecule like RNA be constructed randomly?

Evidence:

  • The Miller experiment: bombard non-organic soup with lab-lightning
    => produces organic compounds.

  • Variants of Miller experiment: production of amino acids, bases, sugars.

  • Proteinoids: artificial creation of proteins
    • Heat amino acids (with some substrate) and cool
      => randomly linked amino acids
    • Heat amino acids with some types of clay
      => crystalline structure in clay forces binding of acids.

  • Lab evidence: proteinoids can catalyse some reactions.

RNA-world theory: "First there was RNA"

  • Self-splicing RNA (example: fungal mitochondria)

  • Ribozymes: RNA that can act as an enzyme (example: ribonuclease P)

  • Problems with "RNA-world":
    • What is the likelihood of random creation of RNA?
    • RNA is not very stable.

  • Can simulation help in answering the question: why?
    => was Life an accident?

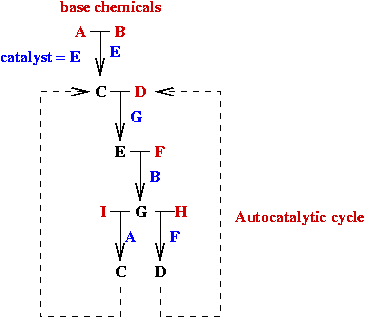
Autocatalysis theory:

  • Motivation: if you create a random soup of chemicals, what is the probability you will see RNA?

  • Alternate question: if you create a random soup of chemicals, what is the probability of seeing an autocatalytic cycle?

  • Problems with random soups:
    • In a random soup, equilibrium may be reached quickly
      => no "new" molecules created.
    • In a random soup, important chemicals may disappear quickly.
    • It takes energy to create large polymers.

  • Autocatalytic cycle:

    A chain of "self-propagating" reactions.

  • Interesting question: in a random soup, what is the probability of seeing an autocatalytic cycle?

  • Surprising answer: if a random soup is "rich" enough, you will always see one!
    • Rich enough base: enough base chemicals.
    • Rich enough pathways: enough catalysis.
Demo

Cellular Automata and Von Neumann's Quandary

Cellular Automata:

  • What is a cellular automaton?
    • An infinite cellular space - usually a 2D grid:

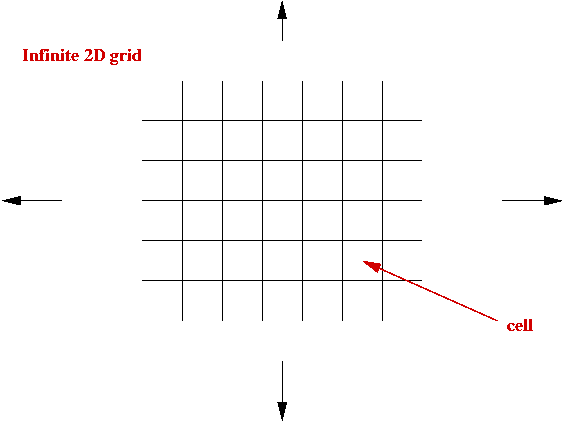
    • Set of states, e.g, S = { empty, A, B, C, D }.

    • Initially each cell is in one of the states:

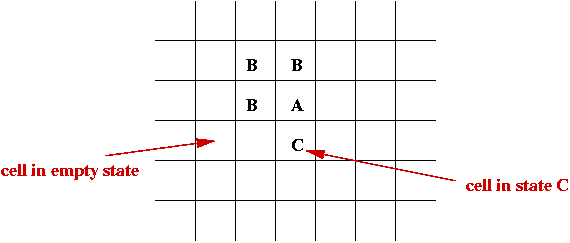
    • System evolves in time-steps.

    • At each step, "rules" are applied to generate the next state for each cell, e.g.,

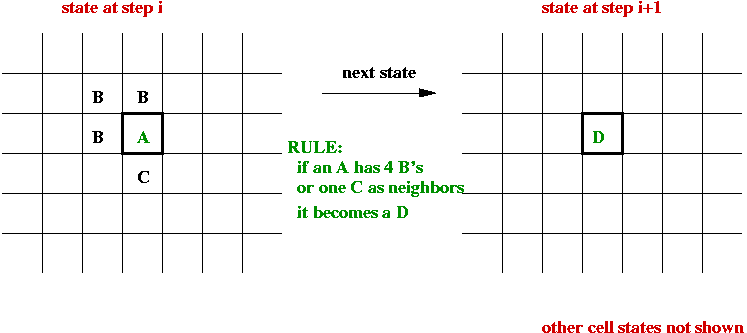
  • State-transition rules:
    • A neighborhood for each cell is defined, usually one of
      • 4-neighborhood (N, S, E, W).
      • 8-neighborhood (N, S, E, W, NE, NW, SE, SW).
    • The next state of a cell depends on its current state and the current state of its neighbors.
    • All cells change state at the same time.
    • The rules are sometimes called the "physics" of the system.

In-Class Exercise 12.3: Search the web for applets that simulate the Game of Life and examine what happens to the following patterns. Run each pattern for a few time steps (generations).

  • The Blinker.

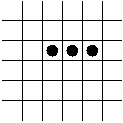
  • The Block.

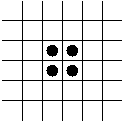
  • The Glider.

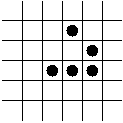
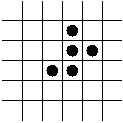
  • The R-pentonimo.

The Game of Life:

  • A cellular automaton with only two states: on and off.

  • Devised in 1970 by John Horton Conway.

  • Rules:
    • Uses 8-neighborhood.
    • Rule 1 (birth): if a cell has exactly 3 neighbors "on", its next state is "on".
    • Rule 2 (status-quo): if a cell has exactly 2 neighbors "on", its next state is its current state.
    • Rule 3 (death): In all other cases, the next state is "off".

  • A generalization: k-Game-of-Life
    • Birth rule: if a cell has exactly k neighbors "on", its next state is "on".
    • Status quo rule: if a cell has exactly k-1 neighbors "on".
    • Death rule: all other values.

  • k = 3 in the Game-of-Life.

  • Interesting observation:
    • If k > 3: too much growth (chaos).
    • If k < 3: too little growth (empty space).
    • k = 3 is "optimal for life".

Von Neumann's quandary:

  • Problem: to prove (mathematically) that self-reproduction is possible.

  • First attempt: the kinematic model (robots):
    • Can a robot reproduce, i.e., assemble a copy of itself (that can later reproduce) from a blueprint?

  • The blueprint problem: can a blueprint contain itself?

  • Second attempt: cellular automaton.

  • Trivial vs. non-trivial reproduction in cellular worlds:
    • Trivial reproduction: the Blinker in the Game of Life.
    • Von Neumann's criteria for non-trivial reproduction: a cellular automaton that:
      • Can embed a Universal Turing machine (i.e., can compute anything)
      • Can embed a Universal Constructor (i.e., can build from a blueprint).
      • Reproduce itself entirely, including blueprint.

  • Von Neumann (with others) showed that it was possible: by constructing a cellular automaton exhibiting non-trivial self-reproduction:
    • 29 states per cell and 200,000 cells.
    • The "creature" contained a "tape" with instructions (blueprint), and a "constructor arm".
    • Another part of the cellular creature contained a universal Turing machine.

  • Solution of the blueprint problem: the blueprint was "photocopied" into the offspring.

  • Reproduction occurs in two phases:
    1. Build the offspring by reading (interpreting) the blueprint.
    2. Copy over the blueprint into the offspring (without interpreting).

Other developments in cellular automata:

  • The Game-of-Life can support computation (and it's believed) self-reproduction.

  • Simpler non-trivial self-reproducing cellular automata have been found
    => all use "blueprint copying". (Example)

  • Cellular automata have become a field of study with attempts to build "metabolic" creatures (that grow, age, evolve etc).

Intriguing questions and comparison between cellular automata and our "wet" world:

  1. Question: Does the physics/chemistry support "self-reproducing life"?
    Cellular world Yes.
    e.g, Von Neumann's example.
    Wet World Yes.

  2. Question: Does the physics also support trivial reproduction?
    Cellular world Yes.
    Game-of-Life's Blinker
    Wet World Yes.
    Crystalline growth.

  3. Question: Does non-trivial reproduction use the 2-step blueprint model?
    Cellular world Yes.
    All examples
    Wet World Yes.
    DNA replication and interpretation.

  4. Question: Is evolution supported?
    Cellular world Yes.
    In some models.
    Wet World Yes.

  5. Question: Is spontaneous occurrence of "life" possible?
    Cellular world Not known.
    Wet World Current belief: Yes.

  6. Question: Is uncontrolled chaotic growth ("grey goo") possible?
    Cellular world Yes.
    Game-of-Life's R-pentonimo
    Wet World ?

  7. Question: Do the elements of self-reproduction also support computation?
    Cellular world Yes.
    Many examples
    Wet World Yes.
    (next section)