DNA Alignment - A Problem in Computational Biology

First, consider the search problem in genomic databases:

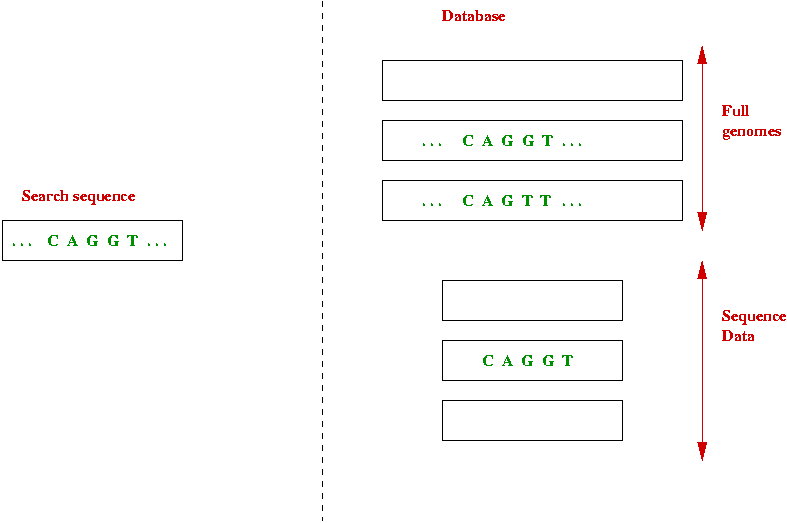
Goal: given a search sequence, find all matches in database of sequences.

Exact-match searches:

• What is an exact match?

  

• Easy to implement, and fast.
  (See pattern search algorithms).

• Practical use of exact-match searches: very little

• Why?

Sequence comparisons:

• We want to allow comparisons such as:

  

Gene comparisons:

• Recall: a gene is a substring of DNA.

• Biologists often compare two genes from different animals to see if they are "similar"
  => to help with gene identification.

• Example: Suppose the DNA sequence A T T T C G C C G T A C encodes a protein in animal X.
  => can search for this gene in animal Y.

• Unfortunately, genes with identical function in different animals are not identical.

• However, they are often similar, e.g.,

  

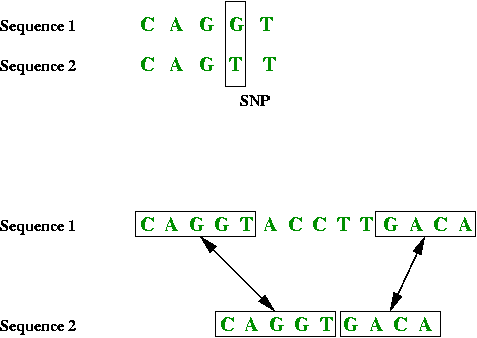
• Sometimes the similarity or "match" is more complex:

  

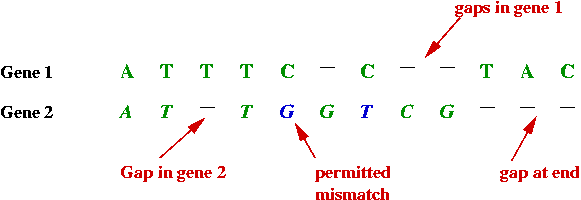
  • By deliberately inserting spaces between the bases in one, a better match can be found.

The alignment problem:

• Define scoring rules for evaluating a particular alignment:
  • Perfectly matched letters get a high score.
  • Matches between related letters get a modest score.
  • Matches with gaps get a low score.

• The alignment problem: given two strings and the scoring rules, find the optimal alignment.

• Problem components:
  • An alphabet, e.g., { A, C, G, T }.
  • Two input strings, e.g.,

    

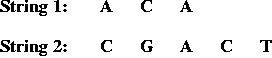
  • Match and gap scores, e.g.,

    

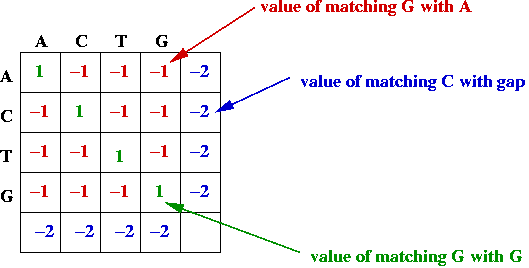
  • Goal: find the alignment with the best (largest) value.

• Potential asymmetry:

  

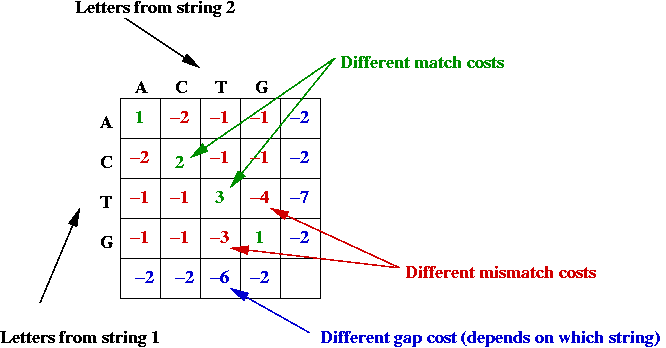
  • Some letter-alignments may be more favored.
  • Some gap costs are different.

• Example:

  

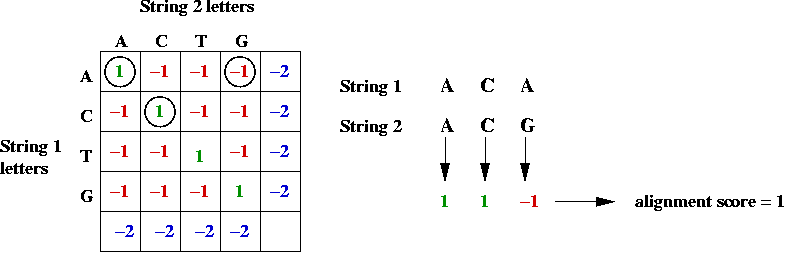
• Example:

  

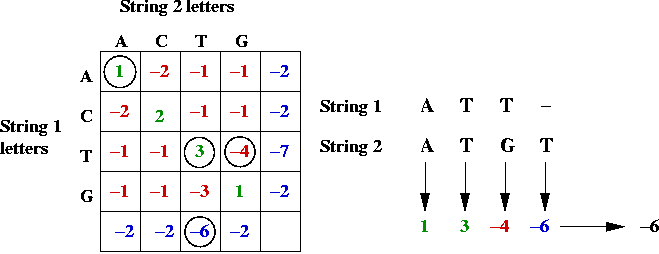
Key ideas in solution:

• First, the alignment problem can be expressed as a graph problem:

  

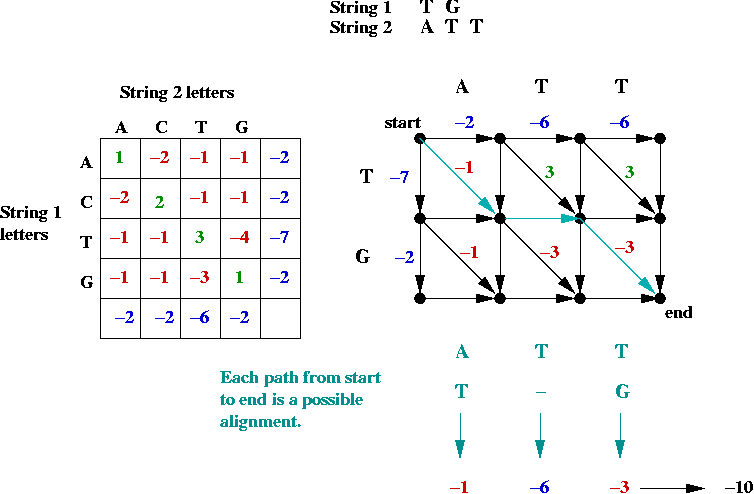
  • The diagonal edges correspond to character matches (whether identical or not).
  • Each down edge corresponds to a gap in string 2.
  • Each across edge corresponds to a gap in string 1.
  • Goal: find the longest (max value) path from top-left to bottom-right.
    => longest-path problem in DAG.
  • Can be solved in O(mn) time (using topological sort)
    (m = length of string1, n = length of string2).
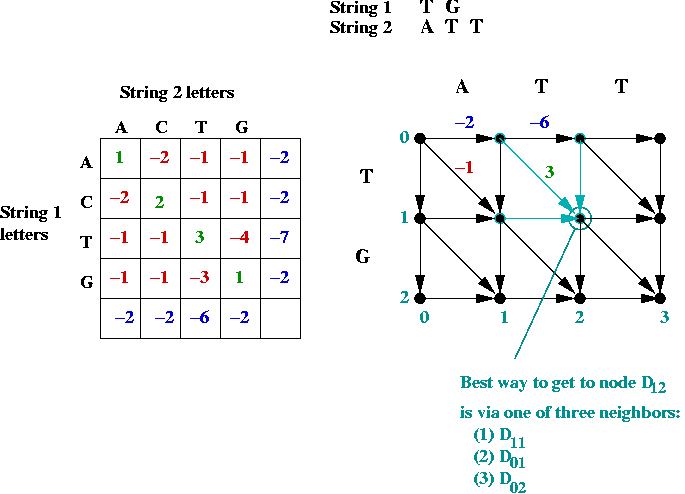
  • Suppose we label the vertices (i, j) where i is the row, and j is the column.
  • The best path to an intermediate node is via one of its neighbors: NORTH, WEST or NORTHWEST.

    

• Dynamic programming approach:
  • Building an actual graph (adjacency matrix etc) is unnecessary.
  • Let D_i,j
    = value of best path to node (i,j) from (0, 0).
    = score of optimal match of first i chars in string 1 to first j chars in string 2.
  • Define (for clarity)

    Ci-1,j-1	=	Di-1,j-1 + exact-match-score
    Ci-1,j	=	Di-1,j + string1-gap-score
    Ci,j-1	=	Di,j-1 + string2-gap-score

  • Thus,

    Di,j	=	max (Ci-1,j-1, Ci-1,j, Ci,j-1
    	=	max (Di-1,j-1 + exact-match-score, Di-1,j + string1-gap-score, Di,j-1 + string2-gap-score)

  • Initial conditions:
    • D_0,0 = 0
    • D_i,0 = D_i-1,0 + gap-score for i-th char in string 1.
    • D_0,j = D_0,j-1 + gap-score for j-th char in string 2.

Implementation:

• Pseudocode:

  Algorithm: align (s1, s2)
  Input: string s1 of length m, string s2 of length n
  
  1.    Initialize matrix D properly;
  
        // Build the matrix D row by row.
  2.    for i=1 to m
  3.      for j=1 to n
  
            // Initialize max to the first of the three terms (NORTH).
  4.        max = D[i-1][j] + gapScore2 (s2[j-1])
  
            // See if the second term is larger (WEST).
  5.        if max < D[i][j-1] + gapScore1 (s1[i-1]) 
  6.          max = D[i][j-1] + gapScore1 (s2[i-1]) 
  7.        endif
  
            // See if the third term is the largest (NORTHWEST).
  8.        if max < D[i-1][j-1] + matchScore (s1[i-1], s2[j-1])
  9.          max = D[i-1][j-1] + matchScore (s1[i-1], s2[j-1])
  10.       endif
  
  11.        D[i][j] = max
  
  12.     endfor
  13.   endfor
  
        // Return the optimal value in bottom-right corner.
  14.   return D[m][n]
  
  Output: value of optimal alignment
     

• Explanation:
  • The 2D array D[i][j] stores the D_i,j values.
  • The method matchScore returns the value in matching two characters.
  • The method gapScore1 returns the value of matching a particular character in string 1 with a gap.
    (gapScore2 is similarly defined).
  • Note: D[i][0] and D[0][j] represent initial conditions.
  • Note: there is one more row than the length of string 1.
    (likewise for string 2).

• Computing the actual alignment:
  • A separate 2D array tracks which term contributed to the maximum for each (i, j).
  • After computing all of D, traceback and obtain path (alignment).

Analysis:

• The double for-loop tells the story: O(mn) to compute D_m,n.

• Note: computing the actual alignment requires tracing back: O(m + n) time (length of a path).

• Space required: O(mn).

An improvement (in space):

• Genes are often longer than 10,000 bases (letters) long
  => space required is prohibitive.

• First, note that we only need successive rows in computing D
  => space requirement can be reduced to O(n).

• However, O(mn) space is still required to construct the actual alignment.

• A different approach:
  • Consider the "middle" character in string 1
    => the character at position m / 2.
  • In the optimal alignment, this character will either align with some j-th character in string 1, or a gap.
    => we can try all possible j values.
  • To try these alignments, compute the m/2-th row (in O(mn) time).
  • Output the optimal alignment found.
  • Recurse on either side of the optimal alignment.

• It is possible to show: O(mn) time and O(n) space.

Variations of the alignment problem:

• Alignment without end-gap penalty
  => do not add costs for gaps at ends.

• Substring alignment
  => find substrings that align.

• Length-based gap penalties
  => the longer a contiguous gap, the more the penalty.

• All have polynomial-time solutions.