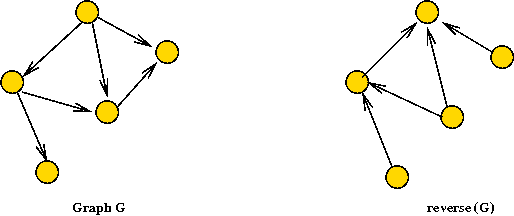Module 7: Graphs, Part I
What is a Graph?
In-Class Exercise 7.0:
Let's start with a simple exercise: The
Calling Circle Problem.
Informal definition:
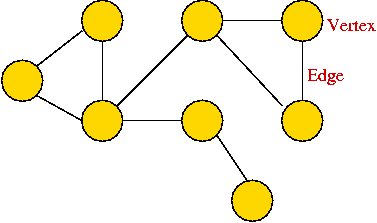
- A graph is a mathematical abstraction used to represent
"connectivity information".
- A graph consists of vertices and edges that
connect them, e.g.,
- It shouldn't be confused with the "bar-chart" or "curve" type
of graph.
Formally:
- A graph G = (V, E) is:
- a set of vertices V
- and a set of edges E = { (u, v): u and v are vertices }.
- Two types of graphs:
- Undirected graphs: the edges have no direction.
- Directed graphs: the edges have direction.
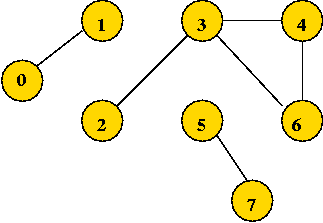
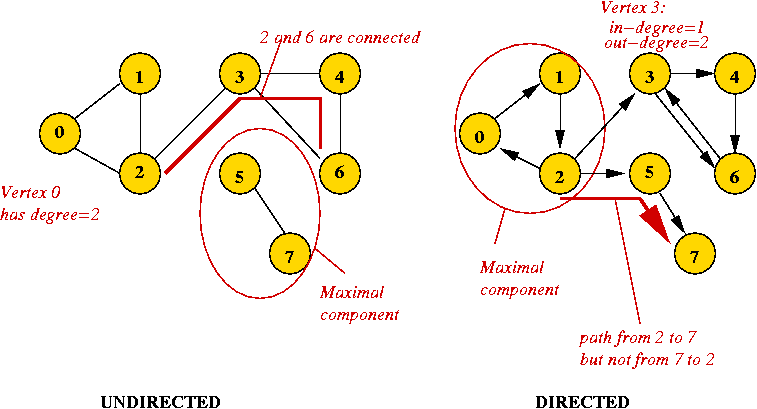
- Example: undirected graph
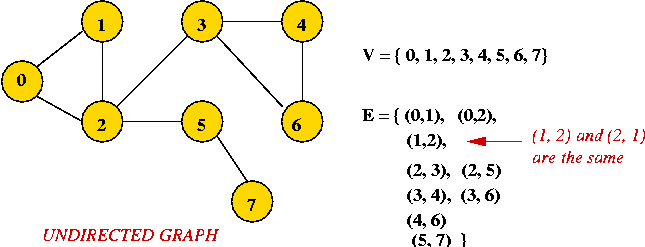
- Edges have no direction.
- If an edge connects vertices 1 and 2, either
convention can be used:
- No duplication: only one of (1, 2) or (2, 1)
is allowed in E.
- Full duplication: both (1, 2) and (2, 1)
should be in E.
- Example: directed graph
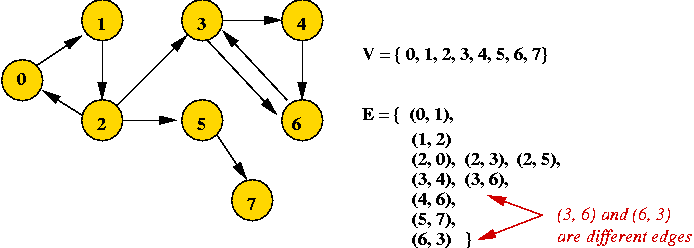
- Edges have direction (shown by arrows).
- The edge (3, 6) is not the same as the edge (6,
3) (both exist above).
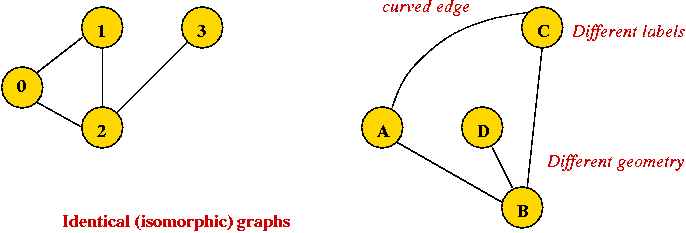
Depicting a graph:
- The picture with circles (vertices) and lines (edges) is
only a depiction
=> a graph is purely a mathematical abstraction.
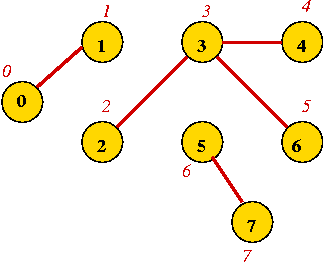
- Vertex labels:
- Can use letters, numbers or anything else.
- Convention: use integers starting from 0.
=> useful in programming, e.g. degree[i] = degree
of vertex i.
- Edges can be drawn "straight" or "curved".
- The geometry of drawing has no particular meaning:
Graph conventions:
- What's allowed (but unusual) in graphs:
- Self-loops (occasionally used).
- Multiple edges between a pair of vertices (rare).
- Disconnected pieces (frequent in some applications).
Example:
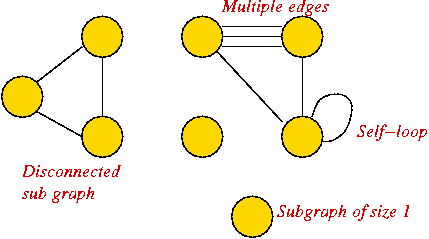
- What's not (conventionally) allowed:
- Mixing undirected and directed edges.
- Re-using labels in vertices.
- Bidirectional arrows.
- Most common:
- No multiple edges.
- No self-loops.
- Other terms used:
- Vertices: nodes, terminals, endpoints.
- Edges: links, arcs.
In-Class Exercise 7.1:
If we disallow multiple edges and self-loops, what is the maximum
number of edges in an undirected graph with n vertices?
What is this number in order-notation?
Definitions:
- Degrees:
- Undirected graph: the degree of a vertex is the
number of edges incident to it.
- Directed graph: the out-degree is the number of (directed) edges
leading out, and the in-degree is the number of
(directed) edges terminating at the vertex.
- Neighbors:
- Two vertices are neighbors (or are adjacent) if
there's an edge between them.
- Two edges are neighbors (or are adjacent) if
they share a vertex as an endpoint.
- Paths:
- Undirected: a sequence of vertices in which successive
vertices are adjacent.
- Directed: a sequence of vertices in which every pair of successive vertices
has this property: there's a directed edge from the first to the second.
- A simple path does not repeat any vertices (and
therefore edges) in the sequence.
- A cycle is a simple path with the same vertex as the
first and last vertex in the sequence.
- Connectivity:
- Undirected: Two vertices are connected if there is a
path that includes them.
- Directed: Two vertices are strongly-connected if there
is a (directed) path from one to the other.
- Components:
- A subgraph is a subset of vertices together with the
edges from the original graph that connects vertices in the subset.
- Undirected: A connected component is a subgraph in
which every pair of vertices is connected.
- Directed: A strongly-connected component is a subgraph
in which every pair of vertices is strongly-connected.
- A maximal component is a connected component that is
not a proper subset of another connected component.
- Digraph: another name for a directed graph.
Example:
More definitions:
Why are graphs important?
- History:
- Applications:
- Fundamental mathematical construct to represent "connectivity".
- Appears in thousands of problems.
- Source of many classic problems: traveling salesman, routing,
spanning trees.
- Many "graph-structured" applications: networks,
transportation-systems, electronic circuits, molecules.
- Source of theory:
- Many important algorithms.
- Key to understanding algorithm design and analysis.
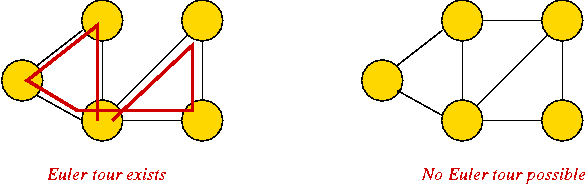
- Simple to describe, yet perplexing:
- Euler tour: easy problem.
- Hamiltonian tour: hard problem.
The field of graph theory:
- Large area of mathematics:
- Analysis of general graphs.
- Analysis of special types of graphs.
- Many classic problems
e.g., the four-color theorem.
- Optimization problems based on graphs,
e.g., shortest-paths.
- Graph algorithms: an area in computer science.
- Rich source of algorithms, theory, insight.
- Useful algorithms used in many applications
(e.g., in a compiler).
In this course:
- Fundamental algorithms for exploring a graph: breadth-first and depth-first.
- Finding shortest paths and minimum spanning tree.
- Convention about undirected vs. directed:
- When not specified, assume undirected.
- Unless otherwise mentioned, an algorithm or definition about
undirected graphs usually can be modified to apply to directed graphs.
(although, directed graphs are usually more complicated).
In-Class Exercise 7.2:
Suppose di is the degree of vertex i in
a connected undirected graph with n vertices and
m edges.
Let D = d1 + ... + dn.
What is the relation between D and m?
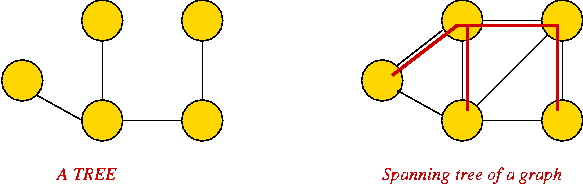
Graph Data Structures
First, an idea that doesn't work:
- We have already represented trees (like binary trees) with node
instances and pointers between instances.
- Idea: use a node instance for each vertex, and a pointer from
one vertex to another if an edge exists between them.
In-Class Exercise 7.3:
Why doesn't it work?
The two fundamental data structures:
- Adjacency matrix.
- Key idea: use a 2D matrix.
- Row i has "neighbor" information about vertex i.
- Undirected: adjMatrix[i][j] = 1 if and only if there's an edge
between vertices i and j.
adjMatrix[i][j] = 0 otherwise.
- Directed: adjMatrix[i][j] = 1 if and only if there's an edge
from i to j.
adjMatrix[i][j] = 0 otherwise.
- Example: undirected
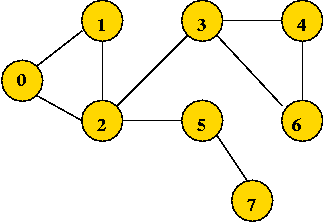
0 1 1 0 0 0 0 0
1 0 1 0 0 0 0 0
0 1 0 1 0 1 0 0
0 0 1 0 1 0 1 0
0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 1
0 0 0 1 1 0 0 0
0 0 0 0 0 1 0 0
Note: adjMatrix[i][j] == adjMatrix[j][i] (convention for
undirected graphs).
- Example: directed
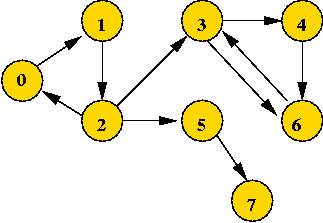
0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0
1 0 0 1 0 1 0 0
0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 1
0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0
- Adjacency list.
- Key idea: use an array of vertex-lists.
- Each vertex list is a list of neighbors.
- Example: undirected
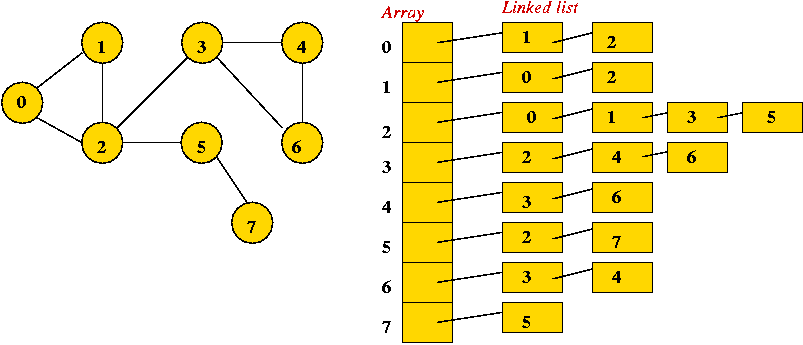
- Example: directed
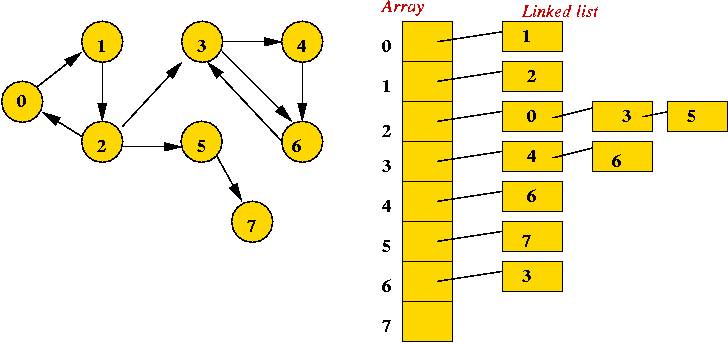
- Convention: in each list, keep vertices in order of insertion
=> add to rear of list
- Both representations allow complete construction of the graph.
- Advantages of matrix:
- Simple to program.
- Some matrix operations (multiplication) are useful in some
applications (connectivity).
- Efficient for dense (lots of edges) graphs.
- Advantages of adjacency list:
- Less storage for sparse (few edges) graphs.
- Easy to store additional information in the data structure.
(e.g., vertex degree, edge weight)
In-Class Exercise 7.4:
Suppose a graph has V vertices and E edges.
In order-notation (in terms of V and E),
what is the size of the adjacency matrix representation?
What is the size of the adjacency list representation?
In-Class Exercise 7.5:
Write a Java class to implement the adjacency list representation.
Do not write all the details, but merely what you need for
initializing the data structure.
Graph ADT:
- ADT = Abstract Data Type.
- What operations should a graph ADT support?
- Insertion of vertices, edges.
- Is the graph connected?
- What are the connected components?
- Does the graph have a cycle?
- Example: consider this interface for an undirected graph ADT:
public interface UndirectedGraphSearchAlgorithm {
// Call this once to set up data structures.
public void initialize (int numVertices, boolean isWeighted);
// Call this repeatedly with each edge to be inserted:
public void insertUndirectedEdge (int startVertex, int endVertex, double weight);
// Return the number of connected components. If "1", then the whole
// graph is connected.
public int numConnectedComponents ();
// Return the component to which each vertex belongs.
public int[] componentLabels ();
// Is there a cycle in the graph?
public boolean existsCycle();
}
In-Class Exercise 7.6:
How would you use this ADT to tell whether a graph is a connected tree?
Next, let's look at some sample code using the matrix
representation:
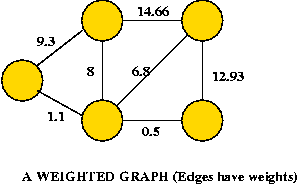
- Convention for weighted graphs: use weight=0 to represent the
lack of an edge.
public class UndirectedGraphSearch implements UndirectedGraphSearchAlgorithm {
int numVertices; // Number of vertices, given as input.
int numEdges; // We keep track of the number of edges.
boolean isWeighted; // Is this a weighted graph?
double [][] adjMatrix; // The matrix. Note: we use "double" to store
// "double" weights, if the graph is weighted.
public void initialize (int numVertices, boolean isWeighted)
{
// Store:
this.numVertices = numVertices;
this.isWeighted = isWeighted;
if (useMatrix) {
// Create the adjacency matrix.
adjMatrix = new double [numVertices][];
for (int i=0; i < numVertices; i++) {
adjMatrix[i] = new double [numVertices];
for (int j=0; j < numVertices; j++)
adjMatrix[i][j] = 0;
}
}
else {
// Adjacency-list representation ...
}
numEdges = 0;
}
// Insert a given input edge.
public void insertUndirectedEdge (int startVertex, int endVertex, double weight)
{
if (useMatrix) {
// Unweighted graph: use weight 1.0.
if (! isWeighted) {
// Insert in both places:
adjMatrix[startVertex][endVertex] = 1.0;
adjMatrix[endVertex][startVertex] = 1.0; // Remove this for directed graphs
}
else {
// Use weight ...
}
numEdges ++;
return;
} // end-use-Matrix.
else {
// Adj-list ...
}
}
The same with an adjacency list:
public class UndirectedGraphSearch implements UndirectedGraphSearchAlgorithm {
int numVertices; // Number of vertices, given as input.
int numEdges; // We keep track of the number of edges.
boolean isWeighted; // Is this a weighted graph?
boolean useMatrix = false; // Adjacency-matrix or list?
LinkedList[] adjList; // The list (of lists): one list for each vertex.
// We are using java.util.LinkedList as our linked list.
// This will store instances of GraphEdge.
// We will test new insertions to see if they exist. Because LinkedList performs
// ".equals()" testing for containment, we need an instance (and only one) of GraphEdge
// for such testing.
GraphEdge testEdge = new GraphEdge (-1, -1, 0);
public void initialize (int numVertices, boolean isWeighted)
{
// Store:
this.numVertices = numVertices;
this.isWeighted = isWeighted;
if (useMatrix) {
// Adjacency matrix creation ...
}
else {
// Adjacency-list representation
adjList = new LinkedList [numVertices];
for (int i=0; i < numVertices; i++)
adjList[i] = new LinkedList ();
// Note: we are using java.util.LinkedList.
}
numEdges = 0;
}
// Insert a given input edge.
public void insertUndirectedEdge (int startVertex, int endVertex, double weight)
{
if (useMatrix) {
// ... Matrix representation ...
}
else {
// Adj-list representation: see if the edge is already there.
testEdge.startVertex = startVertex;
testEdge.endVertex = endVertex;
// Exploit the methods in java.util.LinkedList.
if (adjList[startVertex].contains (testEdge)) {
// ... signal error ...
return;
}
// It's undirected, so add to both vertex lists.
GraphEdge e = new GraphEdge (startVertex, endVertex, 1.0);
adjList[startVertex].addLast (e);
// We wouldn't have this for directed graphs:
GraphEdge e2 = new GraphEdge (endVertex, startVertex, 1.0);
adjList[endVertex].addLast (e2);
numEdges ++;
}
}
Breadth-First Search
About graph search:
- "Searching" here means "exploring" a particular graph.
- Searching will help reveal properties of the graph
e.g., is the graph connected?
- Usually, the input is: vertex set and edges (in no particular order).
Key ideas in breadth-first search: (undirected)
- Mark all vertices as "unvisited".
- Initialize a queue (to empty).
- Find an unvisited vertex and apply breadth-first search to it.
- In breadth-first search, add the vertex's neighbors to the queue.
- Repeat: extract a vertex from the queue, and add its
"unvisited" neighbors to the queue.
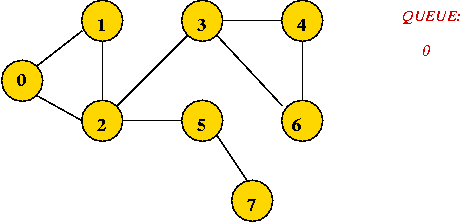
Example:
- Initially, place vertex 0 in the queue.
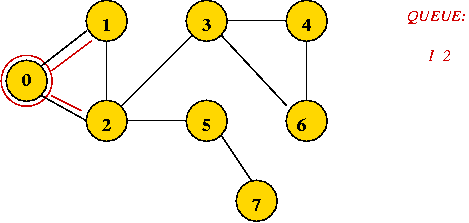
- Dequeue 0
=> mark it as visited, and add its unvisited neighbors to queue:
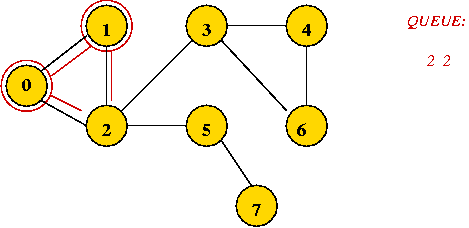
- Dequeue 1
=> mark it as visited, and add its unvisited neighbors to queue:
- Dequeue 2
=> mark it as visited, and add its unvisited neighbors to queue:
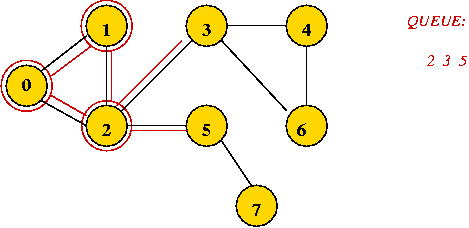
- Dequeue 2
=> it's already visited, so ignore.
- Continuing ...
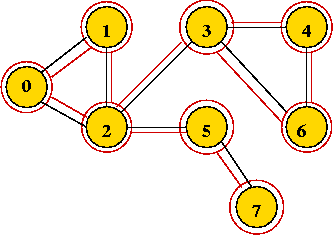
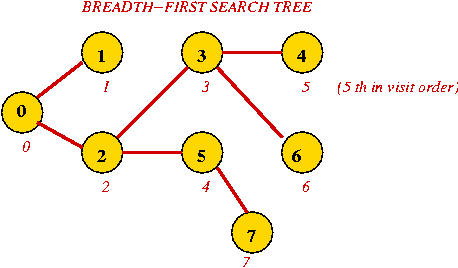
- Breadth-first search tree, and visit order:
- Exploring an edge: examining an unvisited neighbor.
- If an unvisited neighbor gets on the queue for the first time,
the edge is called a "tree edge".
- Putting the tree edges and all vertices together results in:
the breadth-first search tree.
- For a particular graph and its implementation, the tree
produced is unique.
- However, starting from another vertex will result in another
tree, that may be just as useful.
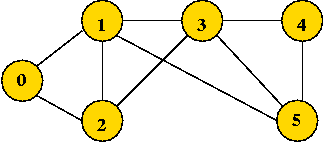
In-Class Exercise 7.7:
What is the visit-order and breadth-first search tree for this graph:
Searching an unconnected graph:
Implementation:
- There are two varieties:
- Allow a vertex to have two states: "unvisited" and "visited"
- An "unvisited" vertex can get placed in the queue multiple times.
It's possible to dequeue a "visited" vertex.
- When dequeueing, check whether vertex was visited.
- Allow three states: "unvisited", "in-queue", and "visited":
- When placing a neighbor in the queue for the first time, mark it as "in-queue".
- Place only "unvisited" neighbors in queue.
=> Queue has only unique, unvisited vertices.
- Extra space required.
- We'll use the former approach, with an adjacency matrix:
- Pseudocode:
Algorithm: breadthFirstMatrix (adjMatrix, n)
Input: A graph's adjacency matrix, number of vertices n.
// Visit order will start with "0", so initialize to -1.
1. for i=0 to n-1
2. visitOrder[i] = -1
3. endfor
// A counter for the order:
4. visitCount = -1
// Standard queue data structure.
5. Create queue;
// Look for an unvisited vertex and explore its tree.
// We need this because the graph may have multiple components.
6. for i=0 to n-1
7. if visitOrder[i] < 0
// We call this "iterative" because other searches are recursive.
8. breadthFirstMatrixIterative (i)
9. endif
10. endfor
Algorithm: breadthFirstMatrixIterative (u)
Input: vertex u, adjMatrix is assumed to be global.
// Queue needs to be reset for each tree.
1. Clear queue;
// Place root of tree on the queue.
2. queue.addToRear (u);
// Continue processing vertices until no more can be added.
3. while queue not empty
// Remove a vertex.
4. v = remove item at front of queue;
// If it hasn't been visited ...
5. if visitOrder[v] < 0
// Visit the vertex.
6. visitCount = visitCount + 1
7. visitOrder[v] = visitCount
// Look for neighbors to visit.
8. for i=0 to n-1
9. if adjMatrix[v][i] = 1 and i != v // Check self-loop: i != v
10. queue.addToRear (i)
11. endif
12. endfor
13. endif
14. endwhile
- A sample Java implementation:
(source file)
import java.util.*;
public class UndirectedBreadthFirstMatrix {
int numVertices; // Number of vertices, given as input.
int numEdges; // We keep track of the number of edges.
boolean isWeighted; // Is this a weighted graph?
boolean useMatrix = true; // Adjacency-matrix or list?
double [][] adjMatrix; // The matrix. Note: we use "double" to store
// "double" weights, if the graph is weighted.
int[] visitOrder; // visitOrder[i] = the i-th vertex to be visited in order.
int visitCount; // We will track visits with this counter.
LinkedList queue; // The queue for breadth-first, a java.util.LinkedList instance.
public void initialize (int numVertices, boolean isWeighted)
{
// ... We've seen this before ...
}
public void insertUndirectedEdge (int startVertex, int endVertex, double weight)
{
// ...
}
//-------------------------------------------------------------------------------
// BREADTH-FIRST SEARCH
// Initialize visit information before search.
void initSearch ()
{
// IMPORTANT: all initializations will use "-1". We will test
// equality with "-1", so it's important not to change this cavalierly.
visitCount = -1;
for (int i=0; i < numVertices; i++) {
visitOrder[i] = -1;
}
}
// Matrix implementation of breadth-first search.
void breadthFirstMatrix ()
{
// 1. Initialize visit variables.
initSearch ();
// 2. Create a queue.
queue = new LinkedList();
// 3. Find an unvisited vertex and apply breadth-first search to it.
// Note: if the graph is connected, the call with i=0 will result
// in visiting all vertices. Nonetheless, we don't know this
// in advance, so we need to march through all the vertices.
for (int i=0; i < numVertices; i++) {
if (visitOrder[i] == -1) {
// We call it "iterative" because depthFirst search is "recursive".
breadthFirstMatrixIterative (i);
}
}
}
// Apply breadthfirst search to a particular vertex (root of a tree)
void breadthFirstMatrixIterative (int u)
{
// 1. A fresh queue is used for a new breadth-first search.
queue.clear();
// 2. Start with the first vertex: add to REAR of queue using java.util.LinkedList.addLast().
// Because LinkedList stores objects, we "objectify" the vertex. A more efficient
// implementation would use a separate queue of int's.
queue.addLast (new Integer(u));
// 3. As long as the queue has vertices to process...
while (! queue.isEmpty()) {
// 3.1 Dequeue and extract vertex using java.util.LinkedList.removeFirst().
Integer V = (Integer) queue.removeFirst();
int v = V.intValue();
// 3.2 If the vertex has been visited, skip.
if (visitOrder[v] != -1)
continue;
// 3.3 Otherwise, set its visit order.
visitCount++;
visitOrder[v] = visitCount;
// 3.4 Next, place its neighbors on the queue.
for (int i=0; i < numVertices; i++) {
// 3.4.1 First, check whether vertex i is a neighbor.
if ( (adjMatrix[v][i] > 0) && (i != v) ) {
// 3.4.1.1 If i hasn't been visited, place in queue.
if (visitOrder[i] == -1) {
queue.addLast (new Integer(i));
}
}
} // end-for
} // end-while
}
} // end-class
Analysis: adjacency matrix
- Assume V vertices and E edges.
- Each vertex is processed V times (worst-case) in starting a tree.
=> O(V).
- Searching for a neighbor: O(V) (scan through matrix).
=> all scans take O(V2).
- Each queue operation is O(1).
- Each edge is processed once:
=> O(E) queue operations and O(E) vertex manipulations.
- Total: O(V2 + E) = O(V2).
Analysis: adjacency list
- Searching for a neighbor: O(# neighbors)
=> total neighbor searches is O(E) (Why?)
- Other operations are the same
Total: O(V + E) = O(E).
In-Class Exercise 7.8:
Which is better: adjacency matrix or adjacency list?
About O(V + E):
- Note that O(V + E) = O(E)
=> it is written as O(V + E) just for emphasis.
- O(V + E) is optimal:
- Every vertex and every edge must be examined.
=> O(V + E)
=> not possible to do better than O(V + E)
- BFS (with adjacency list) is an example of an optimal algorithm.
Directed graphs:
- BFS in directed graphs is similar, except that a vertex's "neighbor" is
one that's reachable by an edge going out from the vertex.
=> search code is identical (but insertion code is different).
Applications:
- Connectivity:
- Breadth-first search identifies connected components.
- However, depth-first search is preferred (required for
directed graphs).
- Shortest paths:
- A path between two vertices in the tree is the shortest path
in the graph.
- Optimization algorithms:
- Various problems result in "graph search space".
- BFS together with "exploration rules" is often used to
search for solutions (e.g., branch-and-bound exploration).
Note: BFS works on a weighted graph by ignoring the weights and
only using connectivity information (i.e., is there an edge or not?).
Depth-First Search on Undirected Graphs
Key ideas:
- Mark all vertices as "unvisited".
- Visit first vertex.
- Recursively visit its "unvisited" neighbors.
Example:
- Start with vertex 0 and mark it visited.
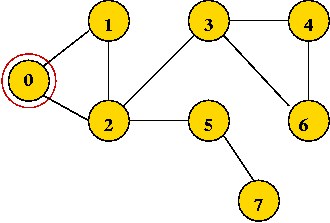
- Visit the first neighbor 1, mark it visited.
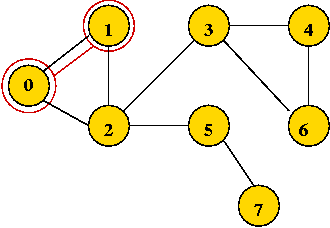
- Explore 1's first neighbor, 2.
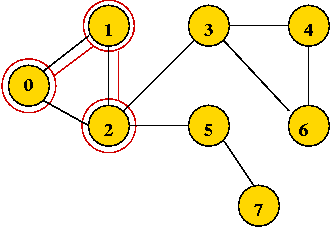
- Continuing until all vertices are visited ...
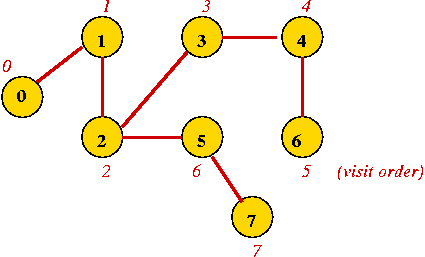
- Vertices are marked in order of visit.
- An edge to an unvisited neighbor that gets visited next is in
the depth-first search tree.
In-Class Exercise 7.9:
What is the visit-order and depth-first search tree for this graph:

Implementation:
- Easier than breadth-first search.
- Pseudocode: adjacency matrix
Algorithm: depthFirstMatrix (adjMatrix, n)
Input: A graph's adjacency matrix, number of vertices n.
// Visit order will start with "0", so initialize to -1.
1. for i=0 to n-1
2. visitOrder[i] = -1
3. endfor
// A counter for the order:
4. visitCount = -1
// Look for an unvisited vertex and explore its tree.
// We need this because the graph may have multiple components.
5. for i=0 to n-1
6. if visitOrder[i] < 0
7. depthFirstMatrixRecursive (i)
8. endif
9. endfor
Algorithm: depthFirstMatrixRecursive (v)
Input: vertex v, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Look for first unvisited neighbor.
3. for i=0 to n-1
4. if adjMatrix[v][i] > 0 and i != v
5. if visitOrder[i] < 0
// If unvisited visit recursively.
6. depthFirstMatrixRecursive (i)
7. endif
8. endif
9. endfor
- Completion order:
- In breadth-first search, once a vertex is processed, it is
never processed again.
- In depth-first, we also encounter a vertex after returning from
the recursive call.
=> we can record a completion order.
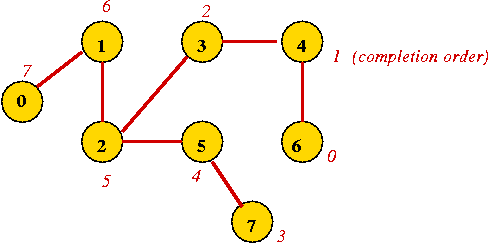
- To record the completion order, simply increment the completion-counter
after the recursion:
Algorithm: depthFirstMatrixRecursive (v)
Input: vertex v, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Look for first unvisited neighbor.
3. for i=0 to n-1
4. if adjMatrix[v][i] > 0 and i != v // Check self-loop.
5. if visitOrder[i] < 0
// If unvisited visit recursively.
6. depthFirstMatrixRecursive (i)
7. endif
8. endif
9. endfor
// After returning from recursion, set completion order:
10. completionCount = completionCount + 1
11. completionOrder[v] = completionCount
- Note: completionCount and completionOrder
need to be initialized (not shown) in depthFirstMatrix.
- Sample Java code:
(source file)
public class UndirectedDepthFirstMatrix {
int numVertices; // Number of vertices, given as input.
int numEdges; // We keep track of the number of edges.
boolean isWeighted; // Is this a weighted graph?
boolean useMatrix = true; // Adjacency-matrix or list?
double [][] adjMatrix; // The matrix. Note: we use "double" to store
// "double" weights, if the graph is weighted.
int[] visitOrder; // visitOrder[i] = the i-th vertex to be visited in order.
int visitCount; // We will track visits with this counter.
int[] completionOrder; // completionOrder[i] = the i-th vertex that completed.
int completionCount; // For tracking.
public void initialize (int numVertices, boolean isWeighted)
{
// ...
}
public void insertUndirectedEdge (int startVertex, int endVertex, double weight)
{
// ...
}
//-------------------------------------------------------------------------------
// DEPTH-FIRST SEARCH
// Initialize visit information before search.
void initSearch ()
{
// IMPORTANT: all initializations will use "-1". We will test
// equality with "-1", so it's important not to change this cavalierly.
visitCount = -1;
completionCount = -1;
for (int i=0; i < numVertices; i++) {
visitOrder[i] = -1;
completionOrder[i] = -1;
}
}
// Matrix implementation of depth-first search.
void depthFirstMatrix ()
{
// 1. Initialize visit variables (same initialization for breadth-first search).
initSearch ();
// 2. Find an unvisited vertex and apply depth-first search to it.
// Note: if the graph is connected, the call with i=0 will result
// in visiting all vertices. Nonetheless, we don't know this
// in advance, so we need to march through all the vertices.
for (int i=0; i < numVertices; i++) {
if (visitOrder[i] < 0) {
depthFirstMatrixRecursive (i);
}
}
}
// Recursive visiting of vertices starting from a vertex.
void depthFirstMatrixRecursive (int v)
{
// 1. First, visit the given vertex. Note: visitCount is a global.
visitCount++;
visitOrder[v] = visitCount;
// 2. Now find unvisited children and visit them recursively.
for (int i=0; i < numVertices; i++) {
// 2.1 Check whether vertex i is a neighbor and avoid self-loops.
if ( (adjMatrix[v][i] > 0) && (i != v) ) {
if (visitOrder[i] == -1) {
// i is an unvisited neighbor.
depthFirstMatrixRecursive (i);
}
}
}
// 3. After returning from recursion(s), set the post-order or "completion" order number.
completionCount++;
completionOrder[v] = completionCount;
}
} // end-class
"Back" and "Down" edges:
- Consider the previous example:
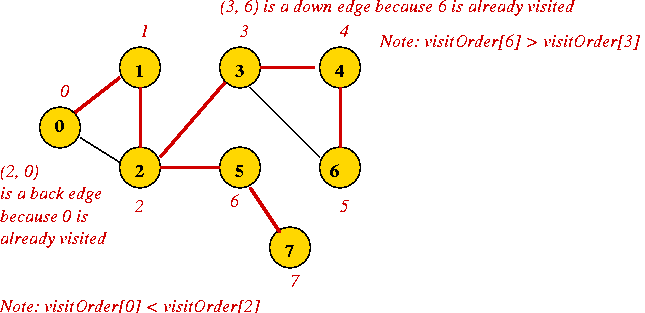
- Back edge
- When vertex 2 probes neighbor 0, 0 has already been visited.
- Vertex 0 is higher up in the tree (ancestor of 2)
=> 0 has a lower visitOrder
=> visitOrder[0] < visitOrder[2].
- The exploration from 2 to 0 is called a back edge.
- Down edge:
- When vertex 3 probes neighbor 6, 6 has already been visited.
- Vertex 6 is lower down in the tree (descendant of 3)
visitOrder[6] > visitOrder[3]
- The exploration from 3 to 6 is called a down edge.
- Let's modify the code to detect back and down edges:
Algorithm: depthFirstMatrixRecursive (u, v)
Input: the vertex u from which this is being called, vertex v
to be explored, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Look for first unvisited neighbor.
3. for i=0 to n-1
4. if adjMatrix[v][i] > 0 and i != v // Check self-loop.
5. if visitOrder[i] < 0
// If unvisited visit recursively.
6. depthFirstMatrixRecursive (i)
7. else if (i != u) // Avoid trivial case.
8. if visitOrder[i] < visitOrder[v]
// Found a back edge.
9. numBackEdges = numBackEdges + 1
10. else
// Found a down edge.
11. numDownEdges = numDownEdges + 1
12. endif
13. endif // visitOrder < 0
14. endif // adjMatrix[v][i] > 0
15. endfor
// After returning from recursion, set completion order:
16. completionCount = completionCount + 1
17. completionOrder[v] = completionCount
- Why identify back and down edges?
- A graph with no back edges revealed by DFS is an acyclic graph.
- Down edges are useful in identifying so-called articulation edges.
Identifying connected components:
- Depth-first search is most often used for identifying connected
components in an undirected graph.
- Key ideas:
- Every time depth-first is re-started (in depthFirstMatrix)
a new component has been found.
create a new component label.
- In the recursion (depthFirstMatrixRecursive), simply
identify each vertex with the current component label.
- Let's re-write (part of) the pseudocode to identify components:
Algorithm: depthFirstMatrix (adjMatrix, n)
Input: A graph's adjacency matrix, number of vertices n.
// Visit order will start with "0", so initialize to -1.
1. for i=0 to n-1
2. visitOrder[i] = -1
3. endfor
// A counter for the order:
4. visitCount = -1
5. completionCount = -1
6. currentComponentLabel = -1
// Look for an unvisited vertex and explore its tree.
// We need this because the graph may have multiple components.
7. for i=0 to n-1
8. if visitOrder[i] < 0
9. currentComponentLabel = currentComponentLabel + 1
10. depthFirstMatrixRecursive (i)
11. endif
12. endfor
Algorithm: depthFirstMatrixRecursive (v)
Input: vertex v, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Mark the component label
3. componentLabel[v] = currentComponentLabel
// Look for first unvisited neighbor...
4. // ... etc (same as earlier version)
- Sample Java code: (source file).
Analysis: adjacency matrix
- Same as breadth-first search: O(V2)
- Why?
- O(1) work for processing each vertex (except for
identifying neighbors).
- O(V) work for identifying neighbors.
=> O(V2) overall.
Analysis: adjacency list
- Similar analysis (to breadth-first search) gives: O(V + E).
- DFS with adjacency list is optimal.
Applications:
- Connectivity: identifying connected components.
=> which earlier-stated problem would this solve?
- Cycle existence.
- Others: finding articulation edges, vertices, "bipartiteness".
- Identifying equivalence classes
Depth-First Search in Directed Graphs
Key ideas:
- A straightforward depth-first search is similar to the
undirected version
=> only explore edges going outward from a vertex in a
directed graph.
- In addition to "back" and "down" edges, it is useful to identify
"cross" edges.
Example:
- Consider: (slightly different from previous example)
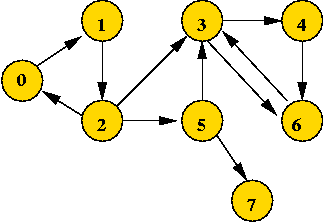
- Applying DFS gives:
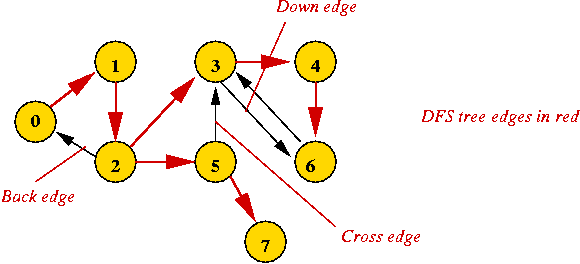
Let's modify the pseudocode to detect cross edges as well:
- Key ideas:
- What used to be a back edge in the undirected version is
now either a back edge or cross edge.
- Back or down edge: when the vertex on the other side
is "visited" but not yet "completed".
- Cross edge: when the vertex on the other side is "completed".
- Pseudocode:
Algorithm: depthFirstMatrixRecursive (u, v)
Input: the vertex u from which this is being called, vertex v
to be explored, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Look for first unvisited neighbor.
3. for i=0 to n-1
4. if adjMatrix[v][i] > 0 and i != v // Check self-loop.
5. if visitOrder[i] < 0
// If unvisited visit recursively.
6. depthFirstMatrixRecursive (i)
7. else if (i != u) // Avoid trivial case.
8. if completionOrder[i] < 0 // Not finished processing i yet
// Found a back edge.
9. numBackEdges = numBackEdges + 1
10. else if visitOrder[i] > visitOrder[v]
// Found a down edge.
11. numDownEdges = numDownEdges + 1
12. else
// Found a cross edge
13. numCrossEdges = numCrossEdges + 1
14. endif
15. endif // visitOrder < 0
16. endif // adjMatrix[v][i] > 0
17. endfor
// After returning from recursion, set completion order:
18. completionCount = completionCount + 1
19. completionOrder[v] = completionCount
Analysis: (same as undirected case)
- Adjacency matrix: O(V2).
- Adjacency list: O(V+E).
Strongly-Connected Components in Directed Graphs
Finding components:
- Recall, in a directed graph a strongly-connected component
is a set of vertices, along with edges associated with
those vertices, such that there is a path
from every vertex in that set to every other in that set.
- Example: vertices 0,1,2 form a strongly-connected component.

In-Class Exercise 7.10:
Describe in pseudocode a simple algorithm to find strongly-connected
components that uses the above DFS algorithm for directed graphs.
Hint: vertices i and j are in the same
strongly-connected component if i is reachable from
j and j is reachable from i.
How long does your algorithm take?
We will look at two different algorithms for finding
strongly-connected components:
- Kosaraju's Algorithm: this applies DFS twice but in an unusual way.
- Tarjan's Algorithm: computes the components directly but is
harder to understand.
Kosaraju's algorithm:
- First, we need to understand the reverse of a directed graph.
- Suppose G = (V,E) is a graph.
- G' = (V,E') is the reverse of G if
E'=E with the direction of edges reversed.
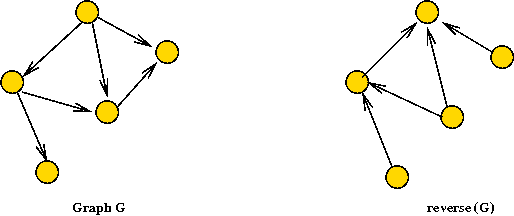
- Next, recall completion-order
lower completion order => closer to root
- The algorithm has two phases:
- First phase: find completion order on reverse graph using
standard DFS.
- Second phase: use a modified DFS on original graph in which
completion order is used as a priority.
- Let's describe the pseudocode first:
Algorithm: stronglyConnectedComponents (adjMatrix, n)
Input: A graph's adjacency matrix, number of vertices n.
1. G' = reverse (G)
2. completionOrder = depthFirstSearch (G')
3. sortOrder = sort vertices in reverse order of completion // Last to first.
4. componentLabels = modifiedDepthFirstSearch (G, sortOrder)
5. return componentLabels
Algorithm: modifiedDepthFirstSearch (adjMatrix, sortOrder)
Input: A graph's adjacency matrix, a sort (priority) order of vertices
1. for i=0 to n-1
2. visitOrder[i] = -1
3. endfor
4. visitCount = -1
5. currentComponentLabel = -1
// Look for an unvisited vertex and explore its tree.
6. for i=0 to n-1
7. v = sortOrder[i] // In order of completion of reverse search.
8. if visitOrder[v] < 0
9. currentComponentLabel = currentComponentLabel + 1
10. modifiedDepthFirstMatrixRecursive (v)
11. endif
12. endfor
13. return componentLabels
Algorithm: modifiedDepthFirstMatrixRecursive (v)
// Mark vertex v as visited and record component label.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
3. componentLabel[v] = currentComponentLabel
// Look for first unvisited neighbor.
4. for i=0 to n-1
u = sortOrder[i] // In order of completion of reverse search.
5. if adjMatrix[v][u] > 0 and u != v
6. if visitOrder[u] < 0
7. depthFirstMatrixRecursive (u)
8. endif
9. endif
10. endfor
Why does this work? The proof is in two parts.
Consider two vertices u and v.
Part (1): Suppose u and v are mutually
reachable:
- Suppose u is visited before v in the second-phase.
- Then, DFS will certainly visit v.
=> The algorithm reports both in the same component.
- The same holds if v is visited before u.
Part (2): Suppose u and v are reported in the
same component by the algorithm:
- Because u and v are in the same reported component,
they are part of a single tree
=> Let w be the root of this tree.
- Then w was visited before u and v.
=> w has a lower completion order than u and v.
(Store this fact for now).
- Next, observe that we reached u from w in
the second phase
=> there's a directed path from w to u in G.
=> there's a directed path from u to w in G'.
- Suppose there is no path from w to u in G'
(the reverse).
=> Then, the path from u to w in G' would
result in u having a higher completion order.
=> Contradiction.
- Thus, there is a path from w to u in G'.
=> There are paths in G from w to u and back.
The same argument shows that there is path from
w to v and back.
=> u and v are mutually reachable in G.
Tarjan's Algorithm:
- Some intuition:
- Consider what happens when we complete processing "3" in
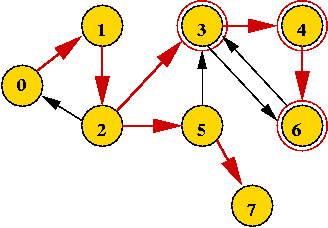
- How can we identify the strong component "3, 4, 6"?
- First, there is no back edge that goes from "4, 6" to any node
"above" 3.
- Second, both "4" and "6" were visited in the descent from "3".
- But nodes "above" 3 will have a lower visitOrder.
=> keep track of lowest visitOrder reachable by a back edge
from a "potential component".
- How to mark vertices in a "component"?
- Build a stack.
- Place vertices on the stack as you recurse down.
- When coming back up the recursion, if you've identified
a component, all vertices in the component are going to be at
the top of the stack.
- Example above: "3, 4, 6" will be on the stack when returning
to "3".
- Another example: "0, 1, 2" will be at the top when returning
to "0".
(It won't be removed along the way back from "3" to "0").
- Pseudocode:
Algorithm: depthFirstMatrixRecursive (u, v)
Input: the vertex u from which this is being called, vertex v
to be explored, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Current lowest reachable:
3. lowestReachable[v] = visitOrder[v];
// Important: minLowestReachable is a local variable so that a
// fresh version is used in each recursive call.
4. minLowestReachable = lowestReachable[v];
// Initialize stackTop to 0 outside. stackTop points to next available.
5. stack[stackTop] = v;
6. stackTop ++;
// Look for first unvisited neighbor.
7. for i=0 to n-1
8. if adjMatrix[v][i] > 0 and i != v // Check self-loop.
9. if visitOrder[i] < 0
// If unvisited visit recursively.
10. depthFirstMatrixRecursive (i)
11. else if (i != u) // Avoid trivial case.
// Identify back, down and cross edges ... (not shown)
12. endif // visitOrder < 0
13. if lowestReachable[i] < minLowestReachable
14. minLowestReachable = lowestReachable[i]
15. endif
16. endif // adjMatrix[v][i] > 0
17. endfor
// We reach here after all neighbors have been explored.
// Check whether a strong component has been found.
18. if minLowestReachable < lowestReachable[v]
// This is not a component, but we need to update the
// lowestReachable for this vertex since its ancestors will
// use this value upon returning.
19. lowestReachable[v] = minLowestReachable
20. return
21. endif
// We've found a component.
22. do
// Get the stack top.
23. stackTop = stackTop - 1
24. u = stack[stackTop];
// We start currentStrongComponentLabel from "0".
25. strongComponentLabels[u] = currentStrongComponentLabel;
// Set this to a high value so that it does not affect
// further comparisons up the DFS tree.
26. lowestReachable[u] = numVertices;
27. while stack[stackTop] != v
28. currentStrongComponentLabel = currentStrongComponentLabel + 1
// After returning from recursion, set completion order... (not shown)
Directed Acyclic Graphs (DAG's)
What are they?
- A DAG is a directed graph without a cycle
=> no path can cause you to revisit a vertex.
- Example:
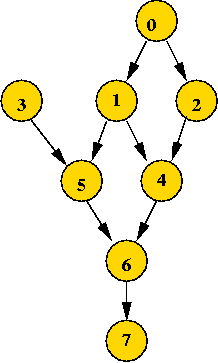
- Example application: task scheduling
- A large activity consists of many related tasks.
- Some tasks need to occur before others.
=> typically a precedence relation among tasks.
- Represent task precedence using a DAG.
Sequential scheduling:
- Suppose the tasks represent programs that must be executed on a
sequential processor.
- Goal: find an execution sequence that does not violate
precedence constraints.
- Example: 3 0 1 2 5 4 6 7
- Note: 4 0 1 2 5 3 6 7 violates precedence requirements.
Topological sort:
- A topological sort of a DAG is a sequence of vertices
that:
- does not violate precedence;
- contains all the vertices.
- A simple (the "classic") algorithm:
- Find a vertex that has no predecessors (zero in-degree)
(there must be one, or it's not a DAG).
- Add this to the sequence.
- Remove it from the graph.
- In removing, adjust the in-degree of every neighbor of the
removed vertex.
- Repeat.
In-Class Exercise 7.11:
Apply the classic algorithm to the above example.
Using depth-first search:
- Key observation: the vertex whose completion occurs
first in depth-first search can be placed last in the sequence.
- Why? It has no successors (descendants in the DFS tree).
- Steps:
- Examine completionOrder in depth-first search.
- Place first vertex to complete at end of sequence.
- Remove it from the graph.
- Place next vertex to complete in next-to-last in sequence.
- ... and so on ...
- Note: after DFS "completes" a vertex, the vertex is never
seen again
=> no need to remove it from graph!
- Example:
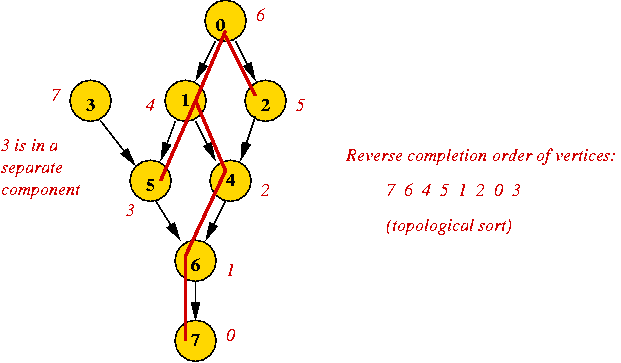
Pseudocode:
- We only need to record topological sort order every time a
completion occurs.
- Partial pseudocode:
Algorithm: depthFirstMatrixRecursive (u, v)
Input: the vertex u from which this is being called, vertex v
to be explored, adjMatrix is assumed to be global.
// Mark vertex v as visited.
1. visitCount = visitCount + 1
2. visitOrder[v] = visitCount
// Look for first unvisited neighbor and recurse
3. for i=0 to n-1
// ... (same as before, not shown) ...
4. endfor
// After returning from recursion, set completion order:
5 . completionCount = completionCount + 1
6. completionOrder[v] = completionCount
// Set topological sort order.
// Initialize topSortCount to -1 outside this method
7. topSortCount = topSortCount + 1
8. topSortOrder[topSortCount] = v