Module 4: Hashing and Tries
Introduction: Signatures and Addresses
We will first consider two aspects of keys:
- Signature: a function computed on keys, usually
resulting in an integer or bit pattern.
- Addressing: where keys are located in memory and what
it takes to reach a particular address.
Signatures:
- Generally, a signature is a function computed on keys
or "texts" that results in an integer or bit pattern for each key.
- The resulting number or bit pattern is called the
"signature" of the key.
- Example: a signature function on strings:
- Let s be a string.
- Suppose signature (s) = "ordinal number of string's
first letter" (from 1,...,26).
We'll call this signature "first letter of string".
- Thus, signature("cat") = 3,
signature("yadayada") = 25,
- A different function:
signature(s) =
concatenation of (7-bit) ascii codes of letters in s.
- Thus, signature("cat") = concatenation of 1100011 (c),
1100001 (a) and 1110100 (t)
= 110001111000011110100.
- Similarly, signature("yadayada") = 1111001 1100001 1100100
1100001 1111001 1100001 1100100 1100001
(with spaces shown only for effect).
- Desired properties:
- Uniqueness: each string (key) should have a unique signature.
- The signature "concatenation of ascii codes" creates
unique signatures.
- The signature "first letter of string" is not unique.
- In practice: keep the probability of sharing a signature small.
- Brevity: signatures should be shorter than the key.
- The signature "first letter of string" is small.
- The signature "concatenation of ascii codes" is not.
- In practice: usually 1-8 bytes, depending on application.
- Efficiency: signatures should be computed quickly.
- The signature "first letter of string" is computed in time O(1)
- The signature "concatenation of ascii codes" is computed
in time O(m) where m is the length of the key.
- Order-preservation: key-order should result in signature-order.
- Both "first letter of string" and "concatenation of ascii
codes" are order-preserving.
- "first letter of string" loses some order information.
- Signatures and order:
- A signature is strictly order-preserving if:
- key1 > key2 implies signature(key1) > signature(key2).
- A signature is order-preserving if:
- key1 > key2 implies signature(key1) >= signature(key2).
- The signature "first letter of string"
is order-preserving (but not strictly order-preserving).
- The signature "last letter of string" is not order-preserving.
- The signature "concatenation of ascii codes" is strictly
order-preserving.
- Signatures can be devised for various kinds of data:
- Strings (as above).
- Geometric data (points, polygons, etc).
- Images.
- Applications:
- Computing a "digest":
- Consider a large text of characters.
- Suppose Signature (text) = sum of ascii codes of characters.
=> every text will have a 7-bit signature.
- If you change the text, the signature is likely to change.
=> applications: security (documents),
change-notification (webpages).
- In practice: larger signatures (e.g., 8 bytes) are used.
- Similarity matching:
- Consider how fingerprints are matched.
- For each fingerprint, a short feature-based signature is computed.
- Matching fingerprints should have matching signatures.
- Data structures: hashing, tries (as we will see).
Addressing:
- Consider a key (e.g., "abc") stored in a data structure.
- The key will usually reside at some memory address.
- To get to this memory address (searching for the key):
- If data structure is linked:
- Linked list: walk down list (O(n)).
- In-order tree: navigate through tree (O(log (n))).
- If data structure is an array:
- Unsorted: scan array (O(n)).
- Sorted: binary search (O(log (n)))
Hashing
Key ideas:
- Hashing combines signatures and addressing.
(Signatures suited for hashing are used).
- The signature is used as the address itself!
- Note: Hashing is intended for equality search.
Two problems:
- Valid addresses:
- If the signature is an integer, how can we use that as a memory
address?
- Some languages (e.g., Java) do not allow direct access to memory.
- Even in C, the signature may not be a valid address.
- Solution: use array offsets.
- Uniqueness:
- What if two keys have the same signature?
=> a collision occurs at the address.
- Solution: store keys together.
Details:
- Create a table (array) with entries 0,...,m-1.
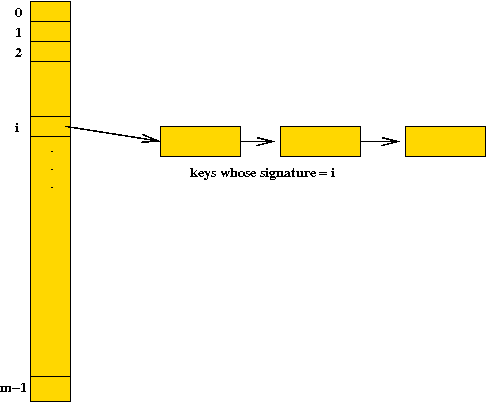
- Each entry represents an address.
- Thus, the addresses are 0,...,m-1.
- Each entry i will contain a linked list used to store keys (and
values) that whose signature (hash value) is i.
- Devise a signature function (called hashing function)
whose output is one of the values 0,...,m-1:
- Suppose a signature function f produces values larger than m.
- Let g(string) = f(string) mod m.
=> g produces values in the range 0,...,m-1.
- Each table entry is sometimes called a bucket.
Example:
- Suppose we want to store the following 51 strings:
"catch",
"throws",
"break",
"byte",
"volatile",
"throw",
"protected",
"this",
"do",
"switch",
"boolean",
"char",
"package",
"true",
"extends",
"new",
"instanceof",
"for",
"public",
"return",
"while",
"case",
"abstract",
"false",
"void",
"synchronized",
"implements",
"finally",
"null",
"try",
"const",
"default",
"native",
"continue",
"super",
"import",
"class",
"final",
"transient",
"short",
"double",
"long",
"private",
"goto",
"int",
"if",
"else",
"static",
"interface",
"float"
- We will use the signature (ascii code of the) "first letter
of string".
- Initially, the hashtable is empty: each entry is an empty
linked list.
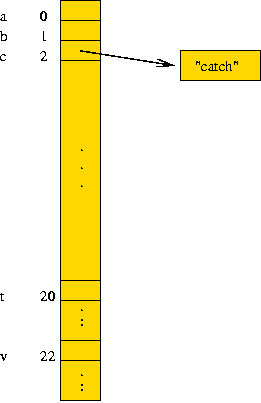
- Next, when inserting "catch":
- Compute signature of "catch": signature("catch") = 2.
(distance from 'a').
- Compute table index: i = signature mod 26.
=> i = 2.
- Insert into linked list at entry 2:
- After inserting "throws", "break", "byte", "volatile":
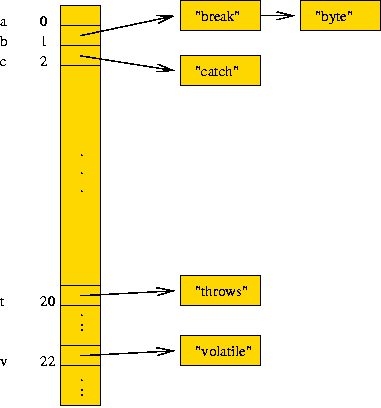
- ... (remaining steps not shown).
Pseudocode:
- Insertion:
Algorithm: initialize (numBuckets)
Input: desired number of buckets
1. Initialize array of linked lists;
Algorithm: insert (key, value)
Input: key-value pair
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
// No list present, so create one
3. table[entry] = new linked list;
4. table[entry].add (key, value)
5. else
6. // Otherwise, add to existing list
7. table[entry].add (key, value)
8. endif
- Search:
Algorithm: search (key)
Input: search-key
// Compute table entry:
1. entry = key.hashCode() mod numBuckets
2. if table[entry] is null
3. return null
4. else
5. return table[entry].search (key)
6. endif
Output: value, if found; null otherwise.
- Note: the add and search methods for linked
lists are not described.
About signatures:
- Signature functions are usually called hash or
hashing functions.
- Hash functions should distribute keys evenly over the
buckets:
- Consider distribution in previous example:
a: 1 ("abstract")
b: 3 ("boolean", "break", "byte")
c: 6 ("case", "catch", "char", "class", "const", "continue")
d: 3 ("default", "do", "double")
e: 2 ("else", "extends")
f: 5 ("false", "final", "finally", "float", "for")
g: 1 ("goto")
h: 0
i: 6 ("if", "implements", "import", "instanceof", "int", "interface")
j: 0
k: 0
l: 1 ("long")
m: 0
n: 3 ("native", "new", "null")
o: 0
p: 4 ("package", "private", "protected", "public")
q: 0
r: 1 ("return")
s: 5 ("short", "static", "super", "switch", "synchronized")
t: 6 ("this", "throw", "throws", "transient", "true", "try")
u: 0
v: 2 ("void", "volatile")
w: 1 ("while")
x: 0
y: 0
z: 0
- In contrast, Java's hashing function has the following
distribution:
table entry 0: 3
table entry 1: 0
table entry 2: 3
table entry 3: 3
table entry 4: 0
table entry 5: 1
table entry 6: 1
table entry 7: 1
table entry 8: 4
table entry 9: 0
table entry 10: 0
table entry 11: 2
table entry 12: 0
table entry 13: 2
table entry 14: 1
table entry 15: 1
table entry 16: 0
table entry 17: 0
table entry 18: 2
table entry 19: 2
table entry 20: 2
table entry 21: 4
table entry 22: 1
table entry 23: 0
table entry 24: 0
table entry 25: 0
(A more even, but not perfect distribution).
- A hashing function should include all parts of the key:
In-Class Exercise 4.1:
Download this template
and the file words (a dictionary).
Print out the distribution of words (only the number) over
buckets for each of the following keys:
- "first letter"
- "last letter"
- Java's hash function.
Hint: you do not have to implement hashing to compute these numbers;
you only need to compute the hash function.
Sizing a table:
- If you expect insertion of n keys, how large should the
table be?
- With m buckets and uniform distribution, there will be
n / m keys per bucket (average).
- Hashing has no guarantees: you can get unlucky and have a large
bucket.
(But probability of large bucket is very small)
- If n is small, consider using a size in the range n
to 4n.
For example: with Java's 51 reserved words and Java's hash
function: we need 287 buckets for a perfect distribution (probably excessive).
- If n is large, use 0.5n or smaller.
- If n is very large, use a hash tree:
- Use a fixed number of buckets (e.g. 100 buckets) at each level.
- Thus, at the root level (level 0) there is the hashtable itself.
- Each bucket is a "child" in the tree.
=>
There are a 100 children at level 1.
- Each node at level 1 can have children (the next level)
=>
There are 100 x 100 = 10,000 children at level 2
- A different hash function is used at each level.
Analysis (assuming few keys per bucket):
- Insertion: O(1) (constant).
- Search: O(1) (constant).
- Both search and insertion times are optimal for the search-problem.
Variations:
- Linear probing:
- Avoid using linked lists: store keys as table entries directly.
- If a collision occurs, simply scan table looking for next
available space.
- Advantage: avoids space for linked structures.
- Disadvantage: long scans occasionally required.
- Double-hashing:
- Like linear-probing, store keys in table.
- Instead of scanning table for available space, use second
hash function to determine where next to try insertion.
- Perfect hashing:
- Given fixed data, design hash functions to ensure perfect
distribution over buckets.
- Use a series of hash functions instead of a single function.
- External hashing:
- For hashing when applied to large disk files (that remain on disk).
- See database course/book for details.
In-Class Exercise 4.2:
Suppose you had to use a hash table for a collection of floating-point
numbers: x1, x2,...,xn.
Design a hashing function to hash to the range 0,...,m.
Geometric Hashing
For a collection of points,
(x1,y1),
(x2,y2),
...,
(xn,yn),
consider the following queries:
- Given a query point q, is q in the collection?
- Given a query point q, what is the nearest point to
q from the collection?
One approach:
- Suppose points are represented by (x,y) values (reals).
- Use a hash function on x-coordinate of each point.
- Can work very well for equality search (first query).
- But nearest-point query?
2D hashing:
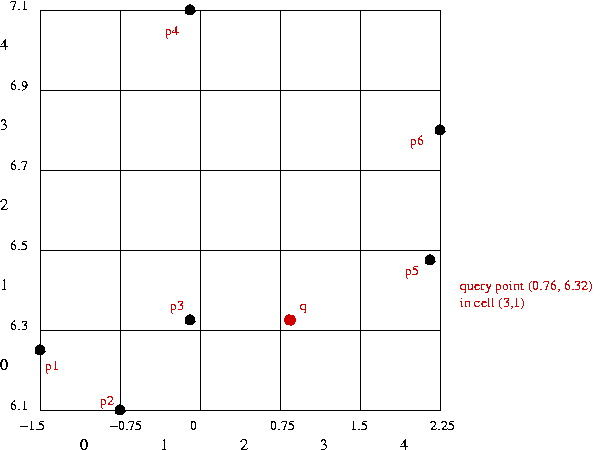
- We'll use this example to illustrate:
- Data:
| p1: | (-1.5, 6.25) |
| p2: | (-0.75, 6.1) |
| p3: | (-0.1, 6.33) |
| p4: | (-0.1, 7.1) |
| p5: | (2.1, 6.48) |
| p6: | (2.25, 6.8) |
- Query point: q = (0.76, 6.32).
- Find minimum x and y values:
xmin = min
(x1,...,xn) = -1.5
ymin = min
(y1,...,yn) = 6.1
- Find maximum x and y values:
xmax = max
(x1,...,xn) = 2.25
ymax = max
(y1,...,yn) = 7.1
- Then, the rectangle with corners
(xmin, ymin),
(xmax, ymax)
is a bounding rectangle.
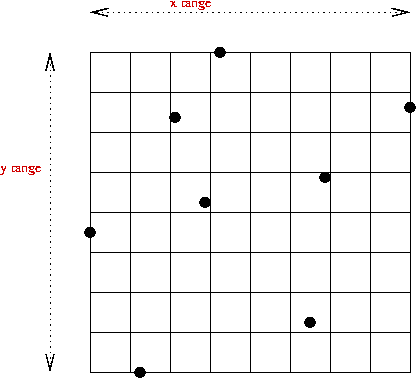
- Divide bounding rectangle into a m x m grid
with m2 cells.
Example with m = 8.
- Give coordinates to each cell, e.g. when m = 5:
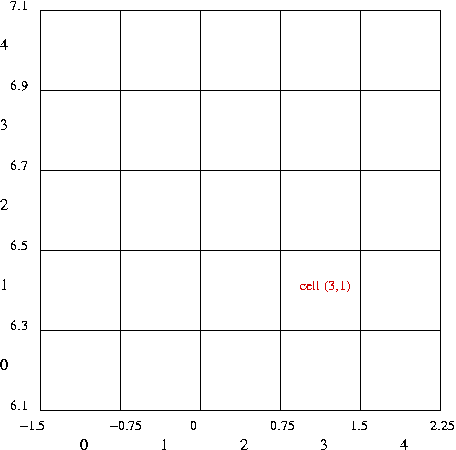
- Each point lies in some cell: use the coordinates as the
2D-hash value.
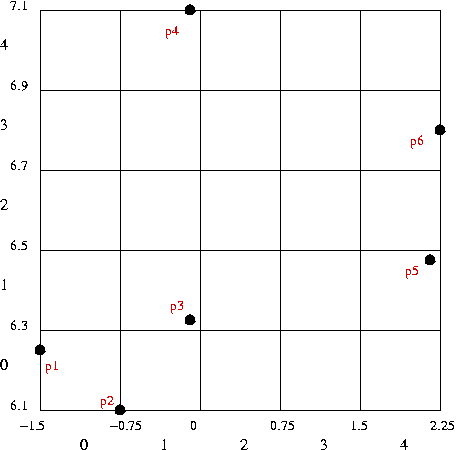
| Point | Coordinates | 2D hash-value |
| p1 | (-1.5,
6.25) | (0,0) |
| p2 | (-0.75,
6.1) | (0,0) |
| p3 | (-0.1,
6.33) | (1,1) |
| p4 | (-0.1,
7.1) | (1,4) |
| p5 | (2.1,
6.48) | (4,1) |
| p6 | (2.25,
6.8) | (4,3) |
- Insert all the points using 2D hash-values:
- Create a 2D table of linked lists (2D hash table).
- Insert each point in appropriate linked list:
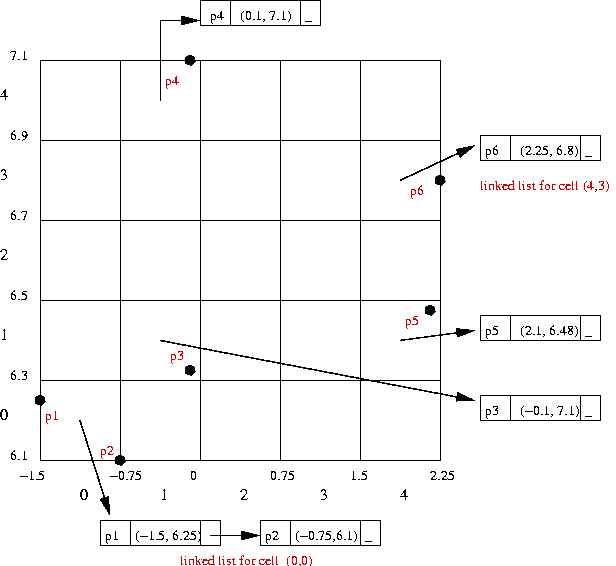
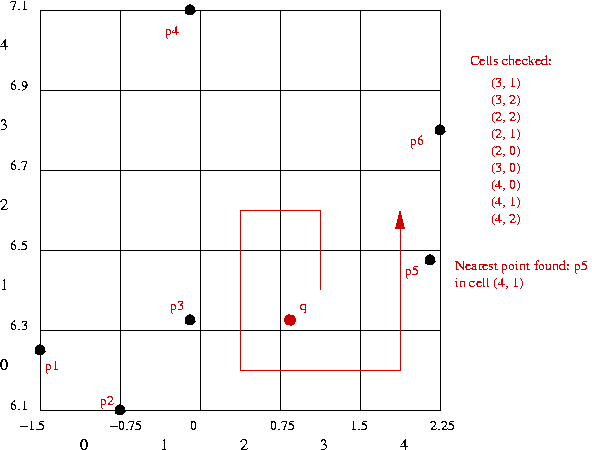
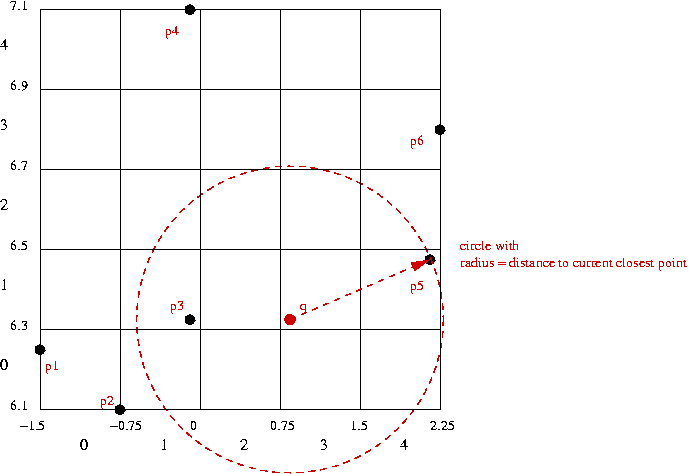
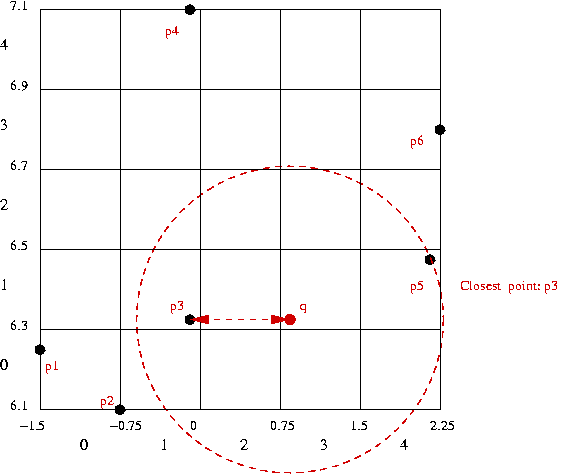
- For nearest-point query:
Tries
Consider combinations of "structure" and whether or not signatures
are used:
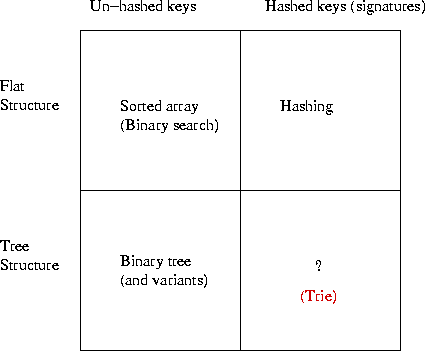
Key ideas:
- Note: "trie" rhymes with "try".
- Use bit-string signature for each key.
Example: "reverse ascii code of first letter in string"
Thus, signature("C") = 1100001.
- At level i, use i-th bit of signature.
- If bit = 0, go left. Otherwise, go right.
- Compare with binary tree:
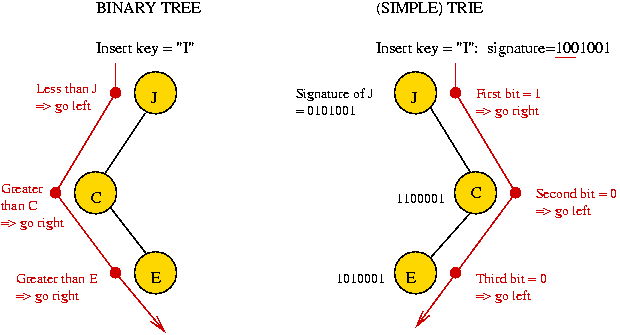
- Note:
- Trie is not necessarily in in-order.
- Different signatures will produce different tries.
- We did not compare with key in node.
- Varieties of tries:
- Simple trie: "store keys in interior nodes".
- Full trie: "store keys in leaves"
- Compressed trie: "store keys in leaves and compress paths",
- Patricia trie: "combination of simple trie and compressed-trie".
Simple Tries
Key ideas:
- Note: Simple tries are also called "Digital Search Trees".
- Insertion: navigate using signature bits until insertion can be made.
- Search: navigate using signature bits, compare with nodes along
the way.
Insertion:
- Example:
- We will use the signature "reverse ascii code of first letter"
(The data happens to have only one letter).
- We will insert the following keys:
| Key | | Signature |
| A | | 1000001 |
| B | | 0100001 |
| C | | 1100001 |
| D | | 0010001 |
| E | | 1010001 |
| F | | 0110001 |
- Insert "A" (1000001)
=> Empty trie, place in root.
- Insert "B" (0100001)
Compare with "A" => not equal, so proceed
First bit = 0 => go left
No link => insert
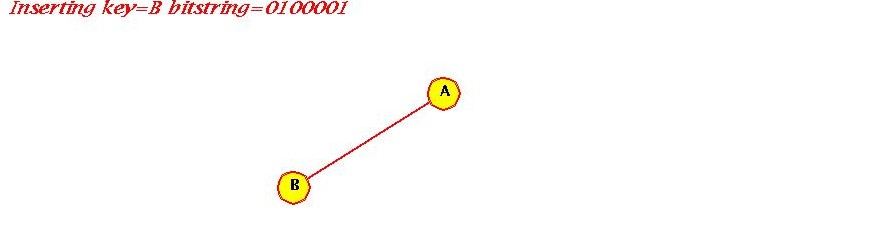
- Insert "C"
Compare with "A" => not equal, so proceed
First bit = 1 => go right
No link => insert
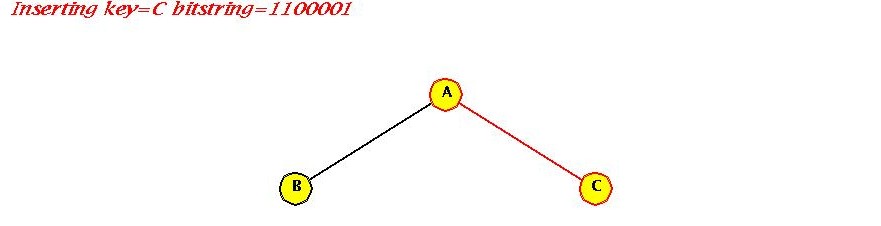
- Insert "D"
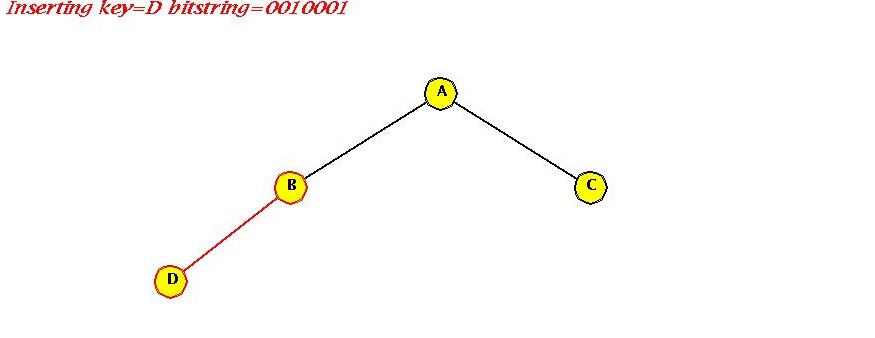
- Insert "E"
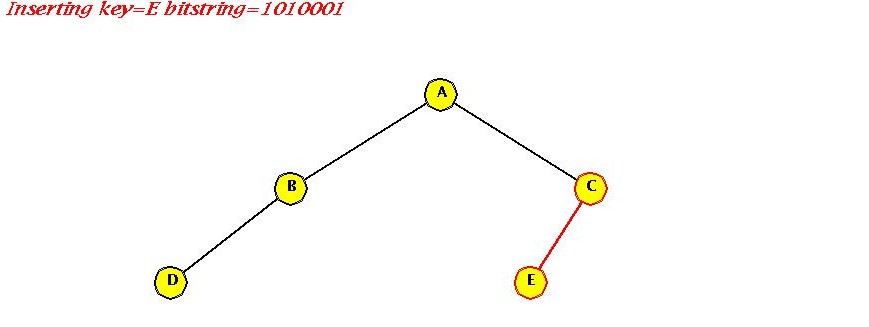
- Insert "F"
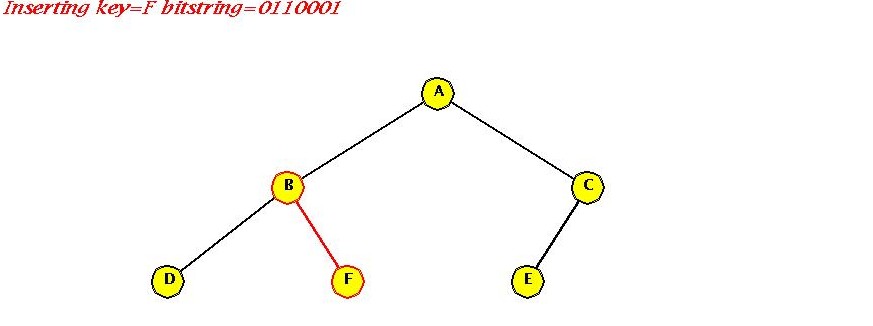
- Pseudocode:
Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = create new root with key-value pair;
3. return
4. endif
// Start numbering the bits from 0.
5. recursiveInsert (root, key, value, 0)
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, which bit we are using now
// Compare with node key to see if it's a duplicate.
1. if node.key = key
2. Handle duplicates;
3. return
4. endif
// Otherwise, examine the bitNum-th bit
5. if key.getBit (bitNum) = 0
// Go left if possible, or insert.
6. if node.left is null
7. node.left = new trie node with key-value;
8. else
// Note: at next level we'll need to examine the next bit.
9. recursiveInsert (node.left, key, value, bitNum+1)
10. endif
11. else
// Same thing on the right
12. if node.right is null
13. node.right = new trie node with key-value;
14. else
15. recursiveInsert (node.right, key, value, bitNum+1)
16. endif
17. endif
Search:
- Search is straightforward:
- Compare the input key with the current node.
- If equal, the key is found; return.
- Otherwise, examine i-th bit (at level i) and go
left or right accordingly.
- If next link is null, search ends without finding the key.
- Pseudocode:
Algorithm: search (key)
Input: search-key
1. node = recursiveSearch (root, key, 0)
2. if node is null
3. return null
4. else
5. return node.value
6. endif
Output: value, if key is found
Algorithm: recursiveSearch (node, key, bitNum)
Input: trie node, search-key, which bit to examine
// Compare with key in node.
1. if node.key = key
// Found.
2. return node
3. endif
// Otherwise, navigate further.
4. if key.getBit (bitNum) = 0
5. if node.left is null
// Not found => search ends.
6. return null
7. else
// Search left.
8. return recursiveSearch (node.left, key, bitNum+1)
9. endif
10. else
11. if node.right is null
// Not found => search ends.
12. return null
13. else
// Search right.
14. return recursiveSearch (node.right, key, bitNum+1)
15. endif
16. endif
Output: trie node if found, else null.
In-Class Exercise 4.3:
Use the "ascii code of first letter" signature to insert "A B C D E F"
into a simple trie. Show all your steps.
Ascii codes are available here.
Analysis:
Full tries
Key ideas:
- Disadvantage of simple trie:
does not maintain sort-order, even if signature
is order-preserving.
- In Full Trie: maintain sort order
Note: must use order-preserving signature.
- To do this: avoid using interior nodes
=> all keys at leaves.
- Interior nodes are for navigation only:
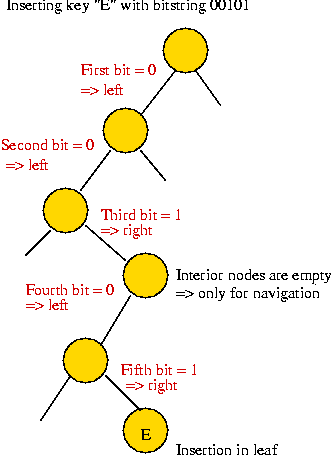
- To sort: scan leaves left to right.
Insertion:
- Key ideas:
- Navigate using bits as long as internal nodes exist.
- If internal node for i-th bit does not exist, create
internal node and all other nodes on path to leaf.
- Note: we will need to know in advance the maximum number of bits.
- Example:
- We will insert the keys (strings) "A", "B", "C", "D", "E", "F".
- Signature: the 5 lowest-order bits of the first letter.
(Note: the data just happens to have only one letter).
- Insert "A" (00001)
- Trie is empty, so create root as well as all internal nodes
on path to leaf node for "A".
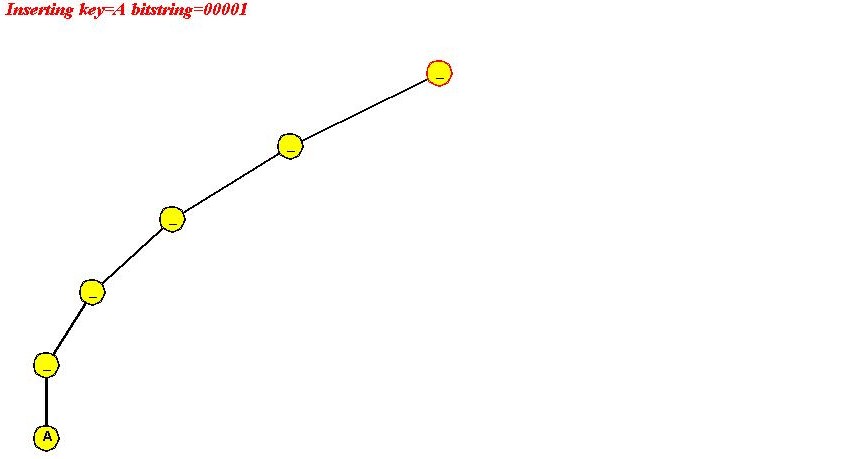
- Insert "B" (00010)
- Traverse left for first three 0's.
- Bit = 1 at 4-th level.
- No internal node exists:
=> create path to leaf.
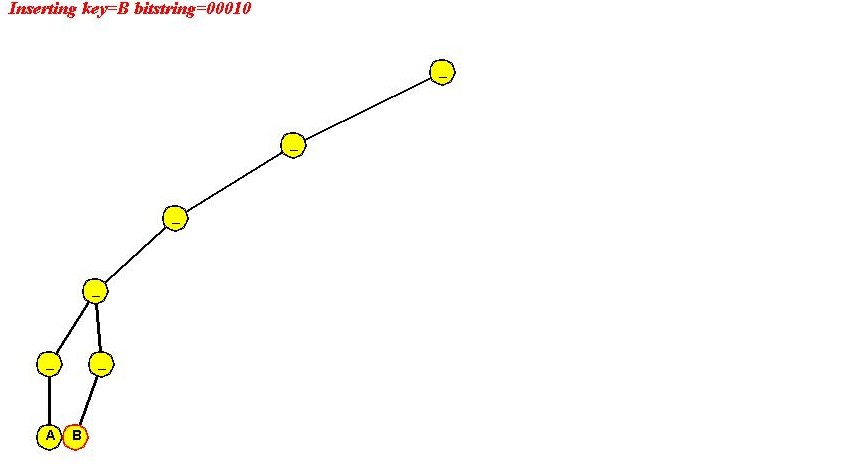
- Insert "C" (00011)
- All internal nodes on path exists
only navigation required (and leaf node).
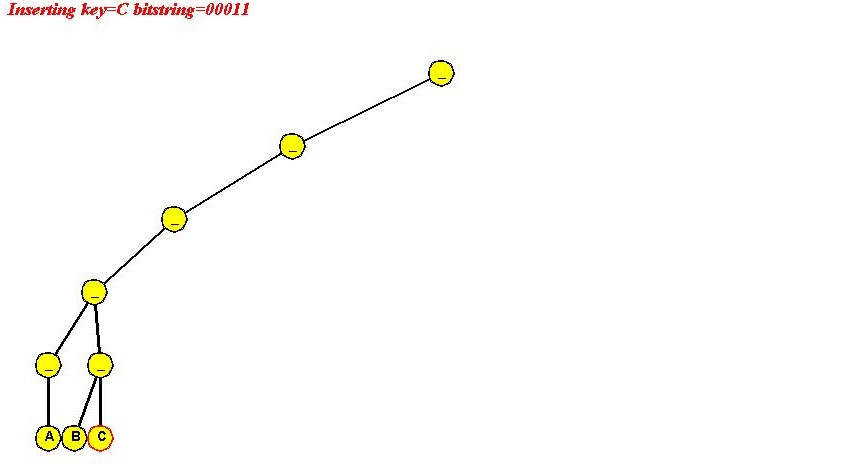
- Insert "D" (00100)
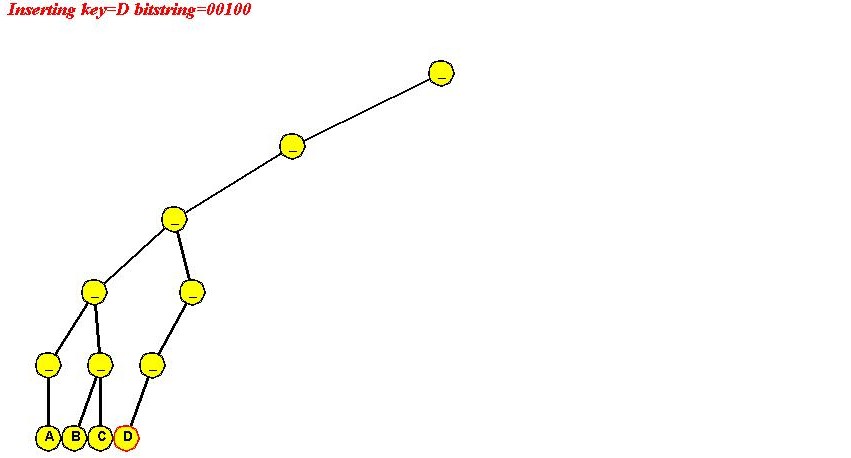
- "E" (00101)
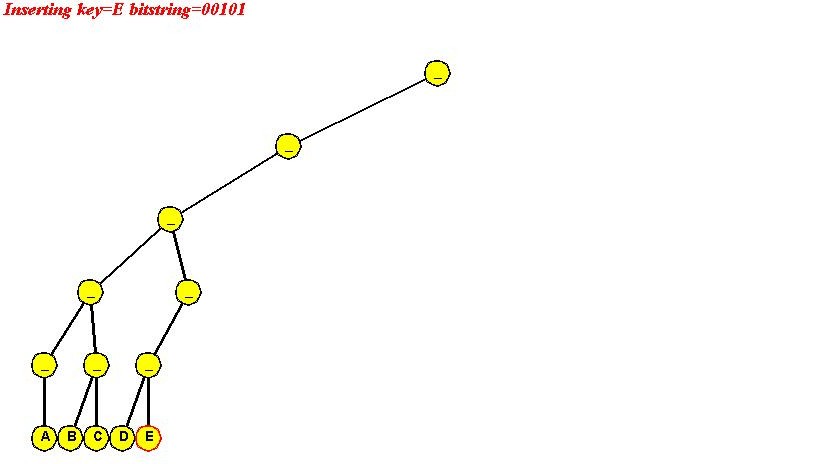
- "F" (00110)
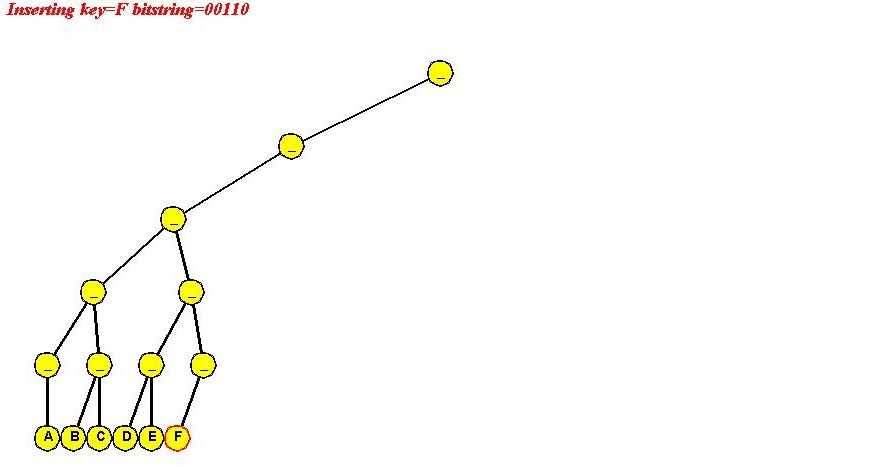
- Pseudocode:
Algorithm: initialize (maxBits)
Input: maximum number of bits
1. Store maximum number of bits to use;
Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = create empty internal node;
// Start bit-numbering at 0 and create path to leaf:
3. extendBranch (root, key, value, 0)
4. return
5. endif
6. recursiveInsert (root, key, value, 0)
Algorithm: extendBranch (node, key, value, bitNum)
Input: internal trie node, key-value pair, bit number
1. Create path of internal nodes from level bitNum to maxBits-1;
2. if key.getBit (maxBits) = 0
3. create left leaf at end of path;
4. else
5. create right leaf at end of path;
6. endif
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, bit number
1. if key.getBit (bitNum) = 0
// Check left side.
2. if node.left is null
// Grow a branch of internal nodes and append leaf.
3. extendBranch (node, key, value, bitNum)
4. else
5. recursiveInsert (node.left, key, value, bitNum+1)
6. endif
7. else
// Check right side.
8. if node.right is null
// Grow a branch of internal nodes and append leaf.
9. extendBranch (node, key, value, bitNum)
10. else
11. recursiveInsert (node.right, key, value, bitNum+1)
12. endif
13. endif
Search:
- Similar to simple trie.
- One difference: compare with keys only at leaves.
Sort-order scan:
- Must use order-preserving signature.
- Since all keys are at leaves
=> in-order traversal will result in sort-order.
- Optimization: link leaves together.
Analysis:
- Again, maximum height = number of bits in signature.
=> log2(n).
- Insertion: O(log (n)).
- Search: O(log (n)).
- Note:
- Simple trie: a key-comparison occurs at each interior node
in search path.
- Full trie: only bit-evaluations occur at internal nodes
=> only ONE key comparison (at leaf)
=> faster search (especially if keys are long).
- Simple trie: One node per key.
- Full trie: multiple (wasted) internal nodes.
=> O(n) extra storage. (Why?)
In-Class Exercise 4.5:
Why is it that the full trie wastes O(n) storage?
In other words, explain why the number of internal nodes
is O(n).
Compressed tries
Key ideas:
- Suppose "D" and "E" are the only keys to the left of the root.
- Common internal nodes are "wasted":
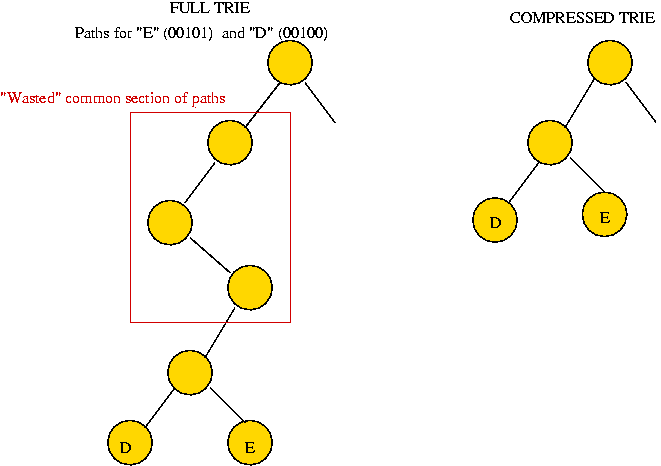
- Compressed trie: compress common sections.
- Idea: during insertion, extend path only as much as needed:
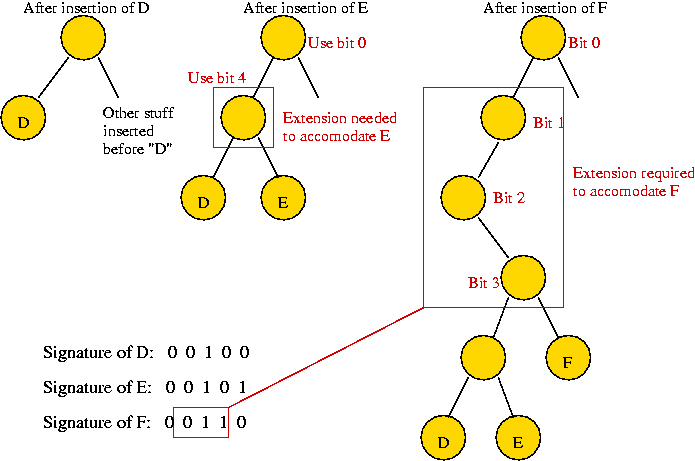
- Note: sort-order is still maintained in leaves.
Insertion:
- Example:
- Insert "A" (00001)
- Trie empty => insert as root.

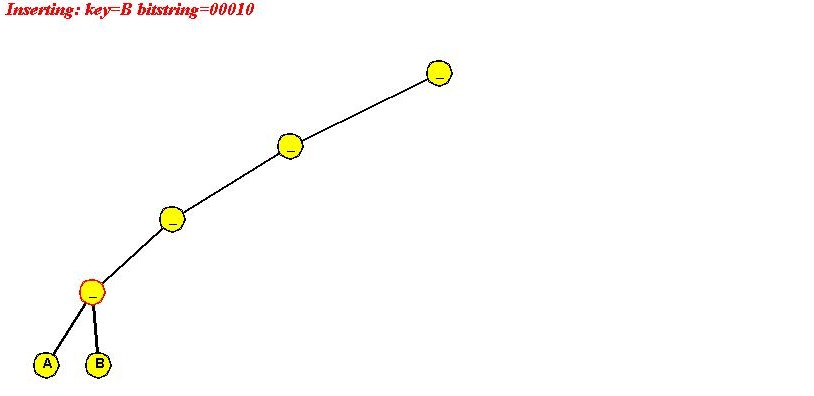
- Insert "B" (00010)
- "B" differs from "A" in fourth bit
=> path of length 3 required.
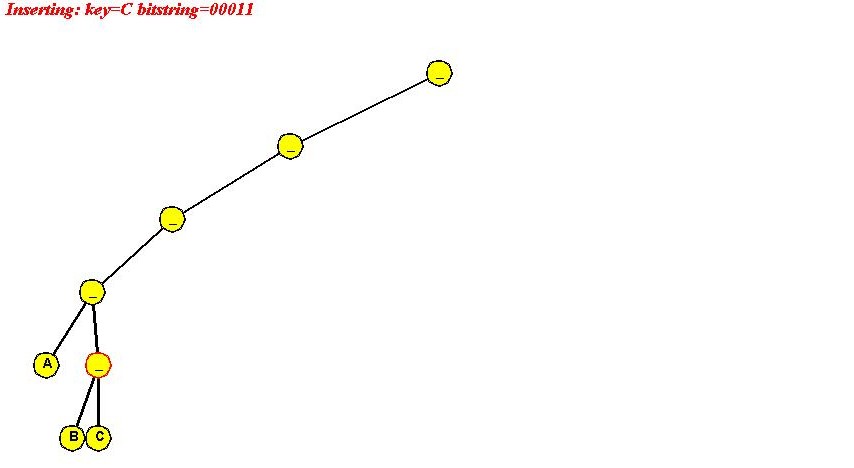
- Insert "C" (00011)
- "C" differs from "B" in last bit
=> full path required
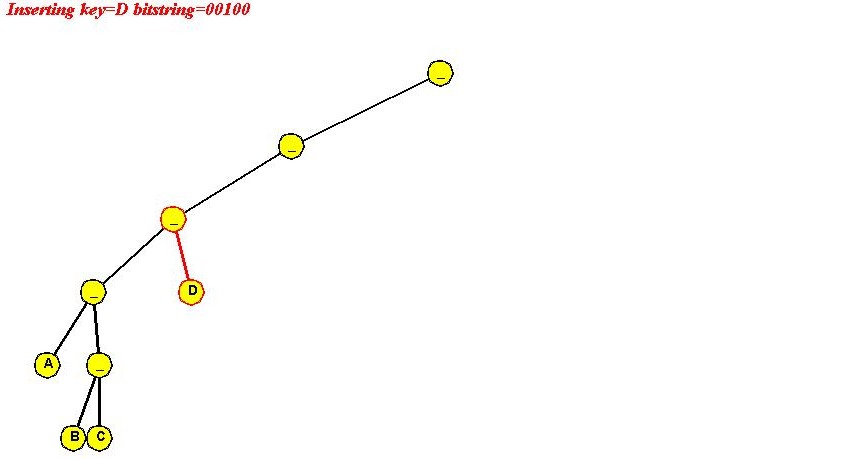
- Insert "D" (00100)
- "D" differs at third bit, no path-creation required.
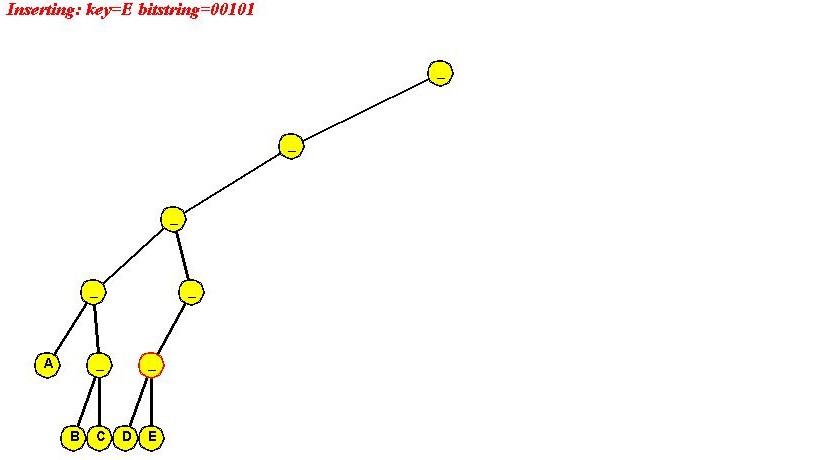
- Insert "E" (00101)
- "E" differs from "D" in last bit
=> path extension required.
- Insert "F" (00110)
- No path creation required.
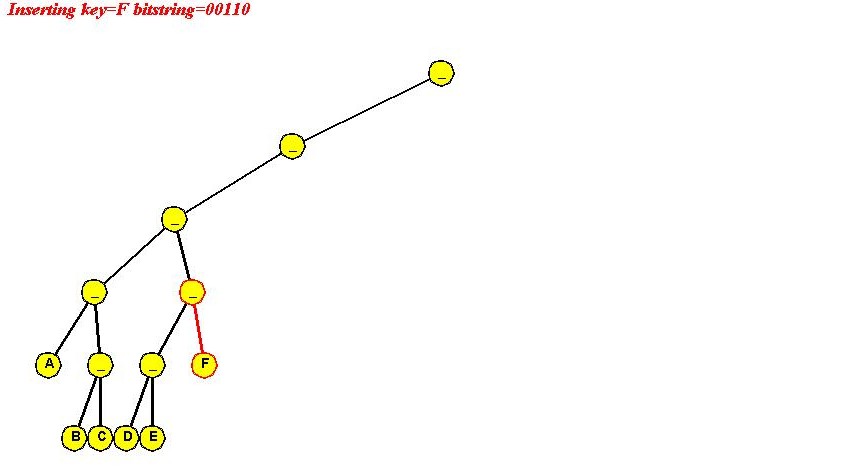
- Pseudocode:
Algorithm: insert (key, value)
Input: key-value pair
1. if trie is empty
2. root = new root node with key-value;
3. return
4. endif
// Start with level 0 (bit number 0):
5. recursiveInsert (root, key, value, 0)
Algorithm: recursiveInsert (node, key, value, bitNum)
Input: trie node, key-value pair, bit number
1. if node contains a key
// Need to create a path to distinguish key and node.key
2. extendSmallestBranch (node, node.key, node.value, key, value, bitNum)
3. return
4. endif
// Otherwise, node is an empty interior node for navigation only.
5. if key.getBit (bitNum) = 0
// Check left.
6. if node.left is null
7. node.left = new node containing key-value;
8. else
9. recursiveInsert (node.left, key, value, bitNum+1)
10. endif
11. else
// Check right.
12. if node.right is null
13. node.right = new node containing key-value;
14. else
15. recursiveInsert (node.right, key, value, bitNum+1)
16. endif
17. endif
Algorithm: extendSmallestBranch (node, key1, value1, key2, value2, bitNum)
Input: node from which to build branch, two key-value pairs, bit number.
// Examine bits from bitNum to maxBits.
// As long as the bits are equal in the two keys, extend branch.
// When the bits differ, stop and create children with key1 and key2.
In-Class Exercise 4.6:
Use the "reverse ascii code of first letter" signature to insert "A B C D E F"
into a compressed trie. Show all your steps.
Ascii codes are available here.
Handling Duplicates (in any Data Structure)
Motivation:
- In practice, data often contains duplicates.
- In some applications, you want to store multiple values
for a single key.
=> data structure should be able to store all values for a key.
Solutions (using Binary Search Tree as data structure):
- Duplicate lists:
- Use the "attached-list" idea from hashing.
- Store duplicates in a linked-list off of tree nodes.
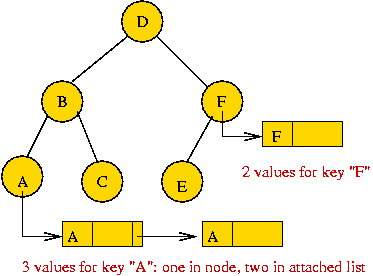
- Advantages: flexible, efficient (only those keys with
duplicates need the list).
- Disadvantages: extra space required in each node.
- Duplicate cache:
- If duplicates are few (O(1)), store in separate table.
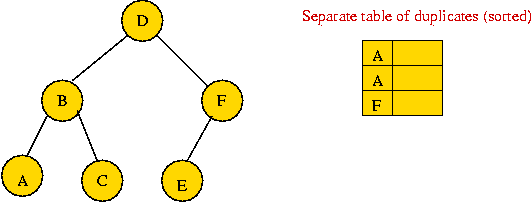
- Constant-cost added to each search (to search cache).
- Advantages: simple, efficient for few duplicates,
interchangeable with data structures.
- Disadvantages: inefficient for many duplicates.
A Java programming trick for handling duplicates:
(source file)
import java.util.*;
public class Duplicate {
// Any Map can be used, e.g., TreeMap.
static Map originalDataStructure = new HashMap();
// Insertion.
static void insert (Object key, Object value)
{
// 1. Attempt a direct insertion.
Object oldValue = originalDataStructure.put (key, value);
// 2. If the value wasn't already there, nothing to be done.
if (oldValue == null) {
// No duplicates.
return;
}
// 3. Otherwise, check if duplicates already exist.
if (oldValue instanceof HashSet) {
// 3.1 There are, so add the new one.
HashSet duplicates = (HashSet) oldValue;
duplicates.add (value);
}
else {
// 3.2 This is the first duplicate => create a HashSet to store duplicates.
HashSet duplicates = new HashSet ();
// 3.3 Place old value and duplicate in hashset.
duplicates.add (oldValue);
duplicates.add (value);
// 3.4 Add the hashset itself as the value.
originalDataStructure.put (key, duplicates);
}
}
// Enumerate and print all values.
static void printAll ()
{
Collection values = originalDataStructure.values();
for (Iterator i=values.iterator(); i.hasNext(); ) {
Object obj = i.next();
// If the value is a HashSet, we have duplicates.
if (obj instanceof HashSet) {
// Extract the different values.
HashSet duplicates = (HashSet) obj;
for (Iterator j=duplicates.iterator(); j.hasNext(); ) {
System.out.println (j.next());
}
}
else {
// If it's not a HashSet, the extract obj is a value.
System.out.println (obj);
}
}
}
public static void main (String[] argv)
{
// Add data with duplicates.
insert ("Ali", "Anorexic Ali");
insert ("Bill", "Bulimic Bill");
insert ("Bill", "Blasphemous Bill"); // Duplicate.
insert ("Chen", "Cadaverous Chen");
insert ("Dave", "Dyspeptic Dave");
insert ("Dave", "Duplicitous Dave"); // Duplicate.
insert ("Dave", "Diabolical Dave"); // Duplicate.
insert ("Ella", "Egregious Ella");
insert ("Franco", "Flatulent Franco");
insert ("Gita", "Gluttonous Gita");
insert ("Gita", "Grotesque Gita"); // Duplicate.
// Print.
printAll();
}
}