Module 3: Search Trees
Introduction: Search
The general search problem:
- Given a collection of data and a "search term", find matching
data from the collection.
Examples:
- Word search in a dictionary
- Dictionary: collection of words (strings), with accompanying "meanings"
- Search term: a word
- Goal: find the word's "meaning", if it exists in the dictionary.
- Similar examples: symbol table search.
- Pattern search in a text
- Text: a large blob of characters.
- Pattern: boolean or regular expression (e.g, "Find 'Smit*' OR 'J*n*s'")
- Goal: find all occurences of pattern in text.
- Similar examples: the Unix grep utility.
- Document retrieval
- A large collection of documents.
- Input: a search string, boolean conditions
- Goal: retrieve all documents containing the string.
- Geometric searching
- Data: list of points
- Input: a query rectangle
- Goal: find all points that lie in the query rectangle
- Similar examples: nearest-point, intersecting objects
- Database search
- Data: collection of relational tables
- Input: a database query (SQL)
- Goal: compute query results (find matching data)
We will divide search problems into the following categories:
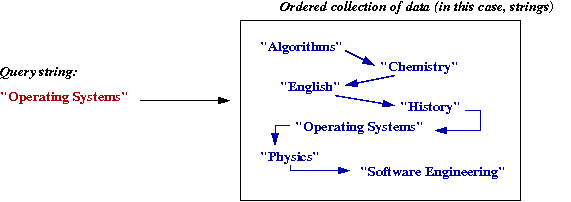
- Ordered Search:
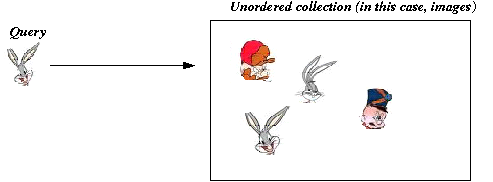
- Equality Search:
- Pattern Search:
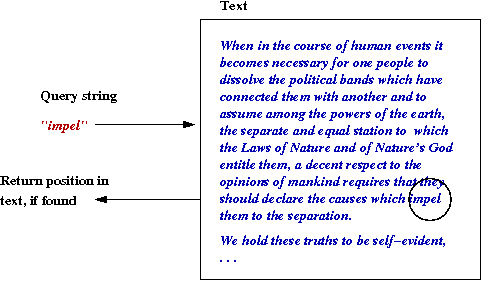
- Data: a large text.
- Input: a query string.
- Goal: find first occurence of the pattern in text.
- Variations: find all occurences.
Algorithms vs. data structures:
- Search "algorithm" usually implies underlying data
structures
=> distinction is blurred.
- Search_solution = data_structure + algorithm_collection
Maps and Sets:
- It is useful to distinguish between a map and a set.
- Set:
- Map:
- Note:
- Most often we will study maps instead of sets.
- "key-value" pair is also used instead of "key-object" pair.
- Often, we will ignore the "value" part since only the "keys"
play a role in searching.
We will say "insert a key" where we mean "insert a key-value pair".
Preview:
- Ordered search:
- Uses natural ordering among items
(e.g., alphabetically-ordered strings).
- For fast navigation: split up data according to order:
=> tree structure
- Examples: binary tree, AVL-tree, multi-way tree,
self-adjusting binary tree, tries
- Equality search:
- Examples: self-adjusting binary tree, hashing
- Pattern search:
- String searches in large texts.
- Boyer-Moore algorithm, finite-automata searching.
In-Class Exercise 3.1:
Download MapSetExample.java
and add code:
- Create an example of a set data structure, add a
few elements to the set, and print those elements at the end.
- Create an example of a map data structure, add a
few elements to the set, and print those elements at the end.
Binary search trees
What is a binary search tree?
- A Binary Search Tree (BST) is a binary tree in in-order.
- The following ordered-search operations are
supported:
- Insertion: insert a key-value pair.
- Search: given a key, return corresponding key-value pair if found.
- Min, max: return minimal and maximal keys in structure.
- Deletion: given a key, delete the corresponding key-value
pair (if found).
- Additional operations: successor, predecessor of keys.
- BST's are implemented using binary trees.
Insertion:
- Key ideas:
- Search to see if it's already there.
- If not, navigate tree looking for the "right" place to insert.
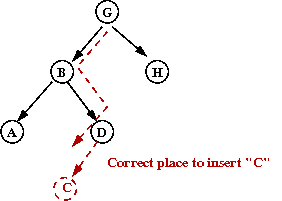
- Go left if key is less than current node, right otherwise.
- Pseudocode:
Algorithm: insert (key, value)
Input: key-value pair
1. if tree is empty
2. create new root with key-value pair;
3. return
4. endif
5. treeNode = search (key)
6. if treeNode not null
// It's already there.
7. Replace old with new;
8. return
9. endif
// Otherwise, use recursive insertion
10. recursiveInsert (root, key, value)
Algorithm: recursiveInsert (node, key, value)
Input: a tree node (root of subtree), key-value pair
1. if key < node.key
2. if node.left not empty
3. recursiveInsert (node.left, key, value)
4. return
5. endif
// Otherwise, append key here.
6. Create new node and append to node.left;
// Otherwise, go right.
7. else
8. if node.right not empty
9. recursiveInsert (node.right, key, value)
10. return
11. endif
// Otherwise, append key here.
12. Create new node and append to node.right;
13. endif
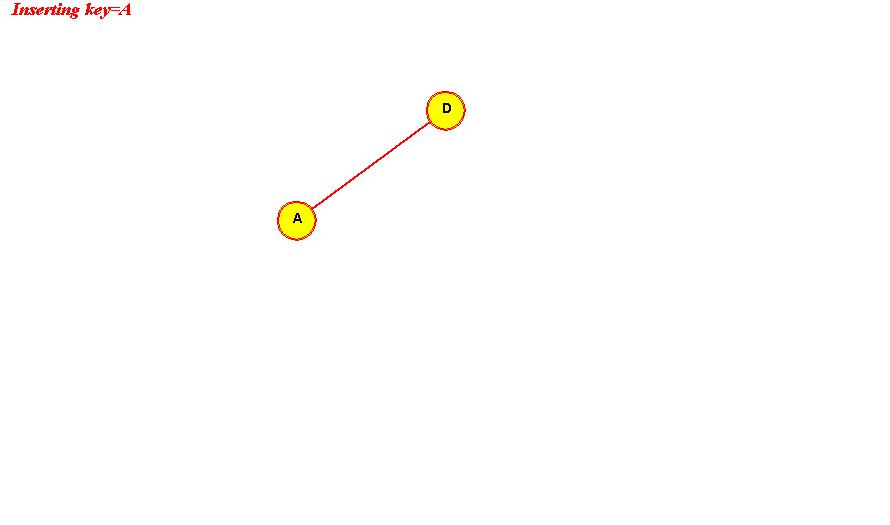
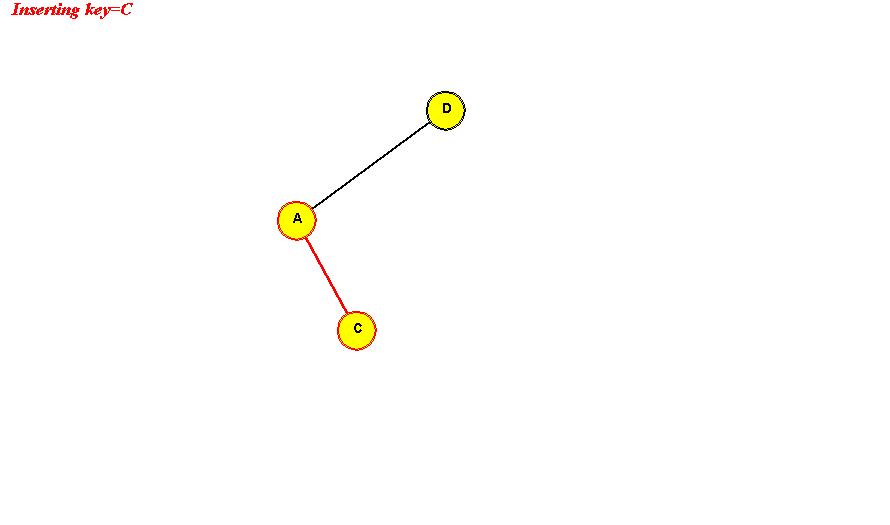
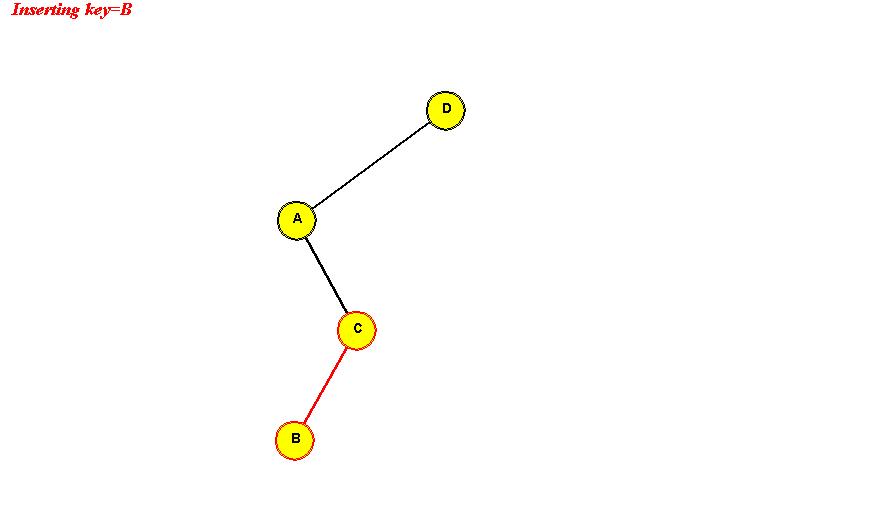
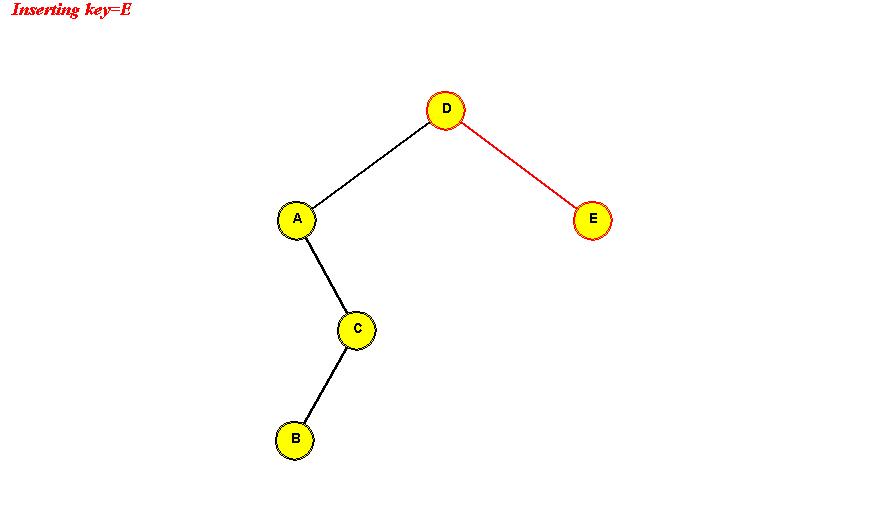
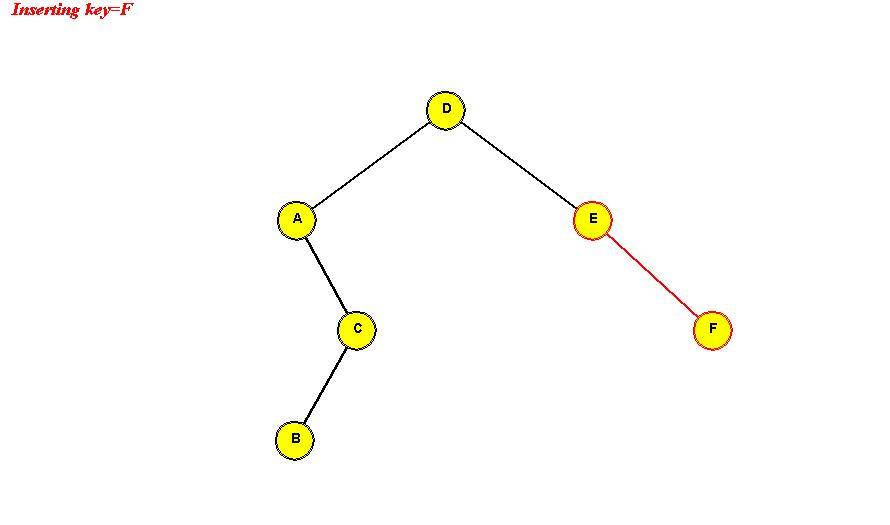
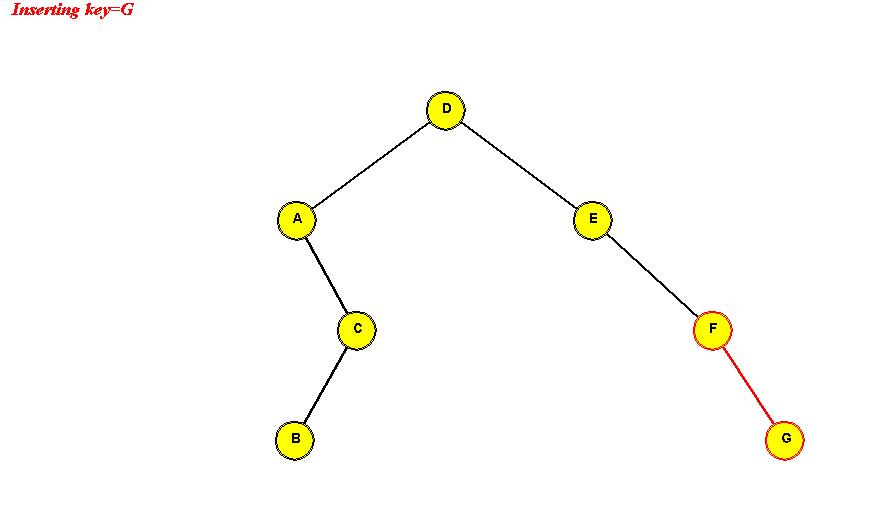
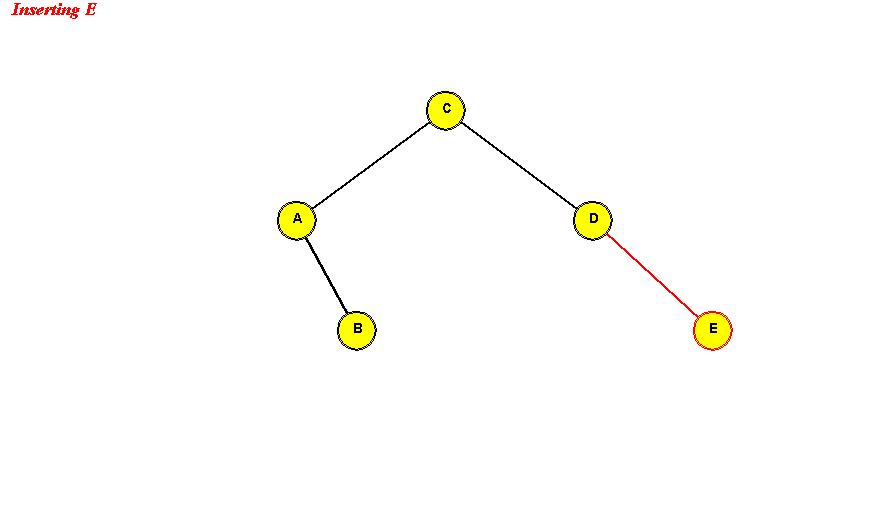
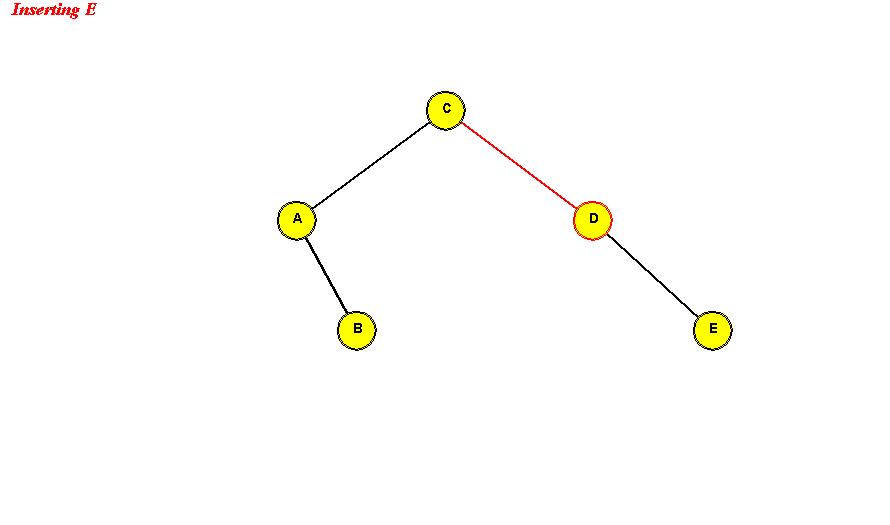
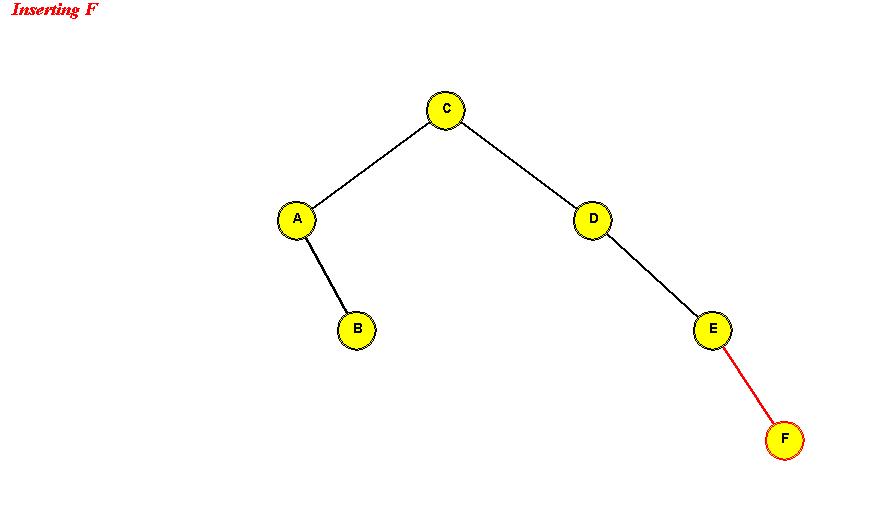
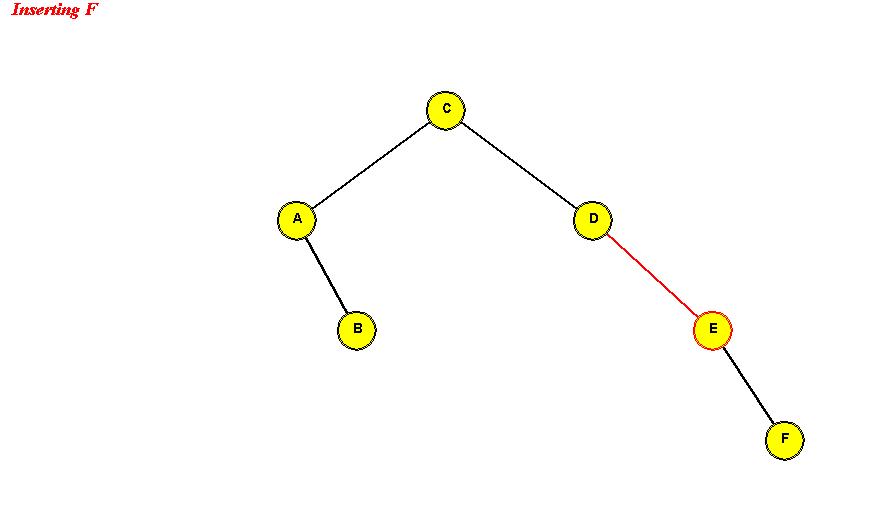
- Example: we will insert the (single-letter) keys "D A C B E F G".
Insert D: "D" becomes the root.
Search:
- Compare with current node; if equal, it's found.
- Otherwise, if the input key is smaller, go left; else go right.
- If, in going left or right, you encounter a null value, the
key does not exist.
Min (and max keys)
- To find the minimum value:
- Start at the root.
- Keep going left until you can't anymore.
- The stopping point has the least value.
- Example (see above tree).
- To find the minimum value in a subtree:
treat the root of the subtree as a root.
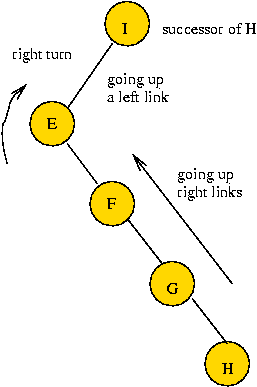
Successors (and predecessors):
- The successor to a particular key is the smallest
key in the tree that is larger than the given key.
- The successor to a particular node is
the successor to the node's key.
- Example: the successor to "E" above is "F".
- Finding the successor to a node:
- If the node has a right child, successor is minimum value in
subtree rooted by right child.
(Intuition: if a node has "stuff" to the right-and-below,
the successor has to be in there).
Note: we already know how to find the minimum element
in a sub-tree (see above).
- If the node does NOT have a right child, there are two
cases:
- Case 1: the node is the root
=> no successor.
- Case 2: the node is not the root
=> successor is between the node and the root.
=> need to walk back up until a "right turn" occurs.
(Intuition: if you are walking up "right links" you get
smaller values, until the turn occurs.)
Deletion:
- Deletion is a little more involved.
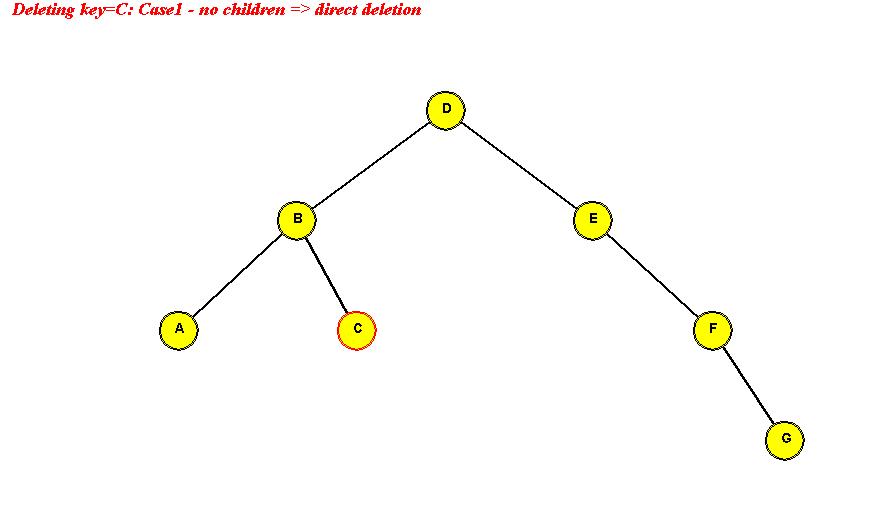
- Case 1: node is a leaf (no children)
- Easy case: simply delete leaf and set pointer to null in parent.
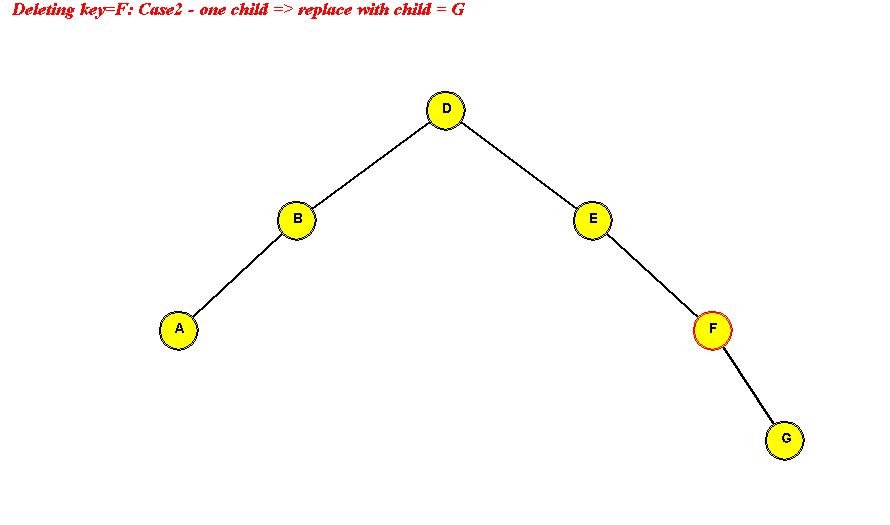
- Case 2: node has one child
=> "splice out" node
=> make the node's child a direct child of node's parent
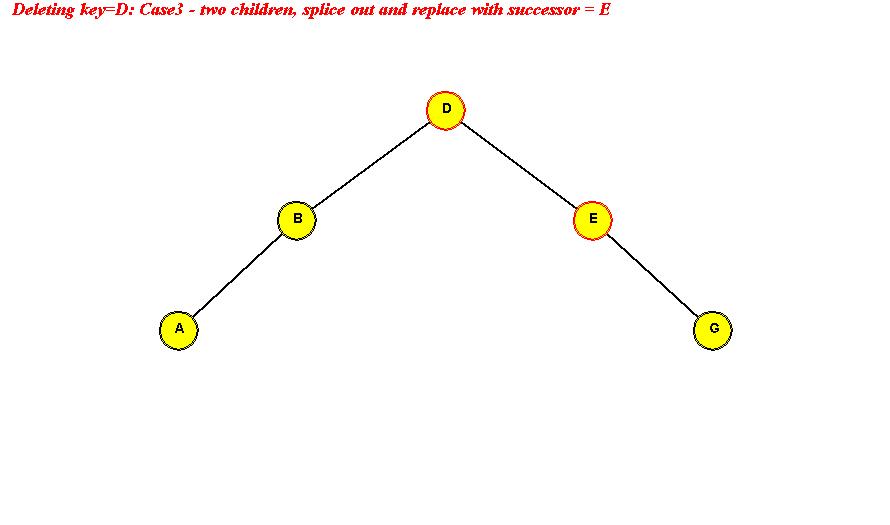
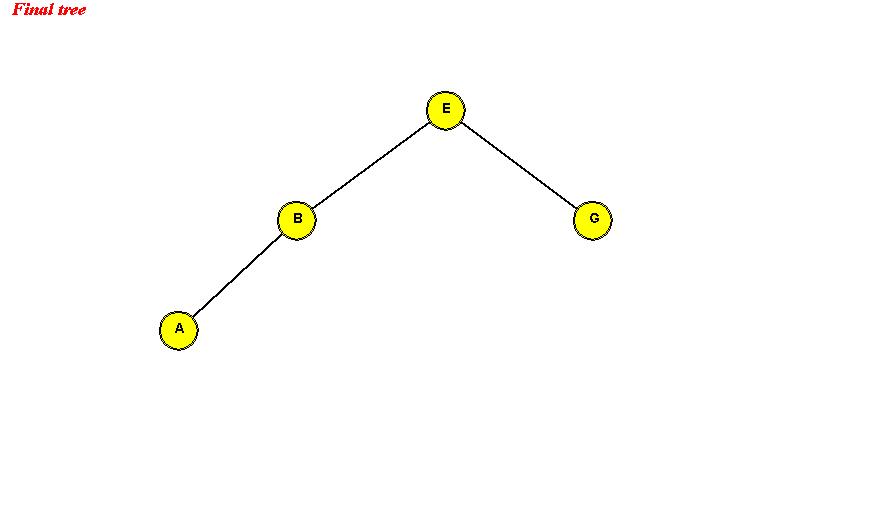
- Case 3: node has two children:
- Example:
In-Class Exercise 3.3:
Insert the following (single-character) elements into a binary tree
and draw the binary tree: "A B C D E F G".
Analysis:
- What are we analysing?
=> Time taken for operations: insert, search, delete.
- Let h be the length of the longest path from the root
to a leaf.
- Time per insert: O(h).
- Time for n insert's: O(nh).
- Time per search: O(h).
- Time per delete:
- O(h) time to find node.
- O(h) time to find successor (if needed)
- O(1) (constant) time to splice, replace.
=> total time: O(h).
- Worst case: h = n.
- Best case: h = log(n).
In-Class Exercise 3.4:
- For a balanced binary tree with n nodes, show that
the height is O(log2(n). Start by computing
the number of nodes in a balanced binary tree when it's
height is h.
- For a balanced ternary tree (three-way branching at each
node) with n nodes, what is the height?
AVL trees
Motivation:
- Binary search trees can get very "unbalanced" quite easily
e.g., when data inserted is almost-sorted.
- AVL idea: why not enforce balance?
Key ideas:
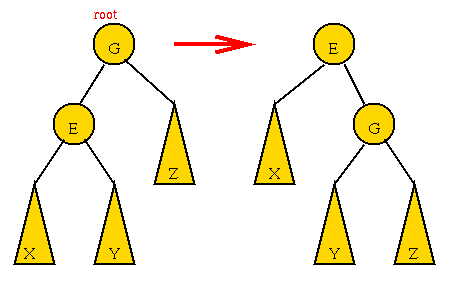
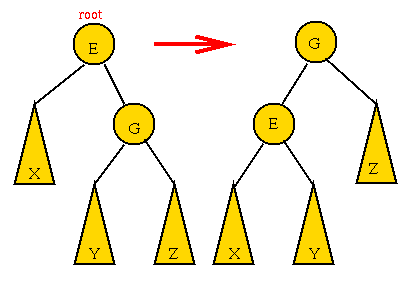
Rotations:
- The (sub) tree rooted at G is unbalanced.
left-height is larger.
=> rotate left-child of G into root position:
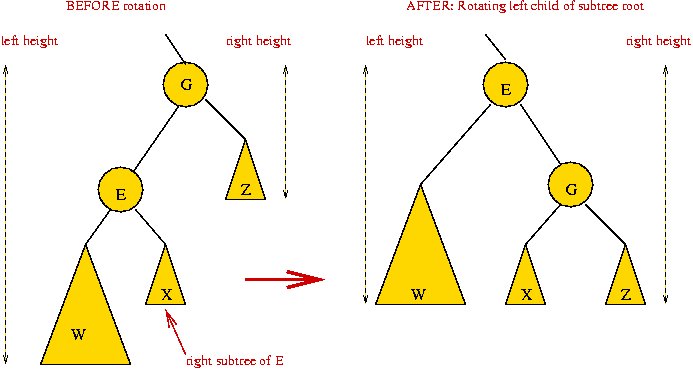
Note:
- Rotation preserves in-order.
- The letters W,X and Z above refer to whole subtrees whereas
E and G are single nodes.
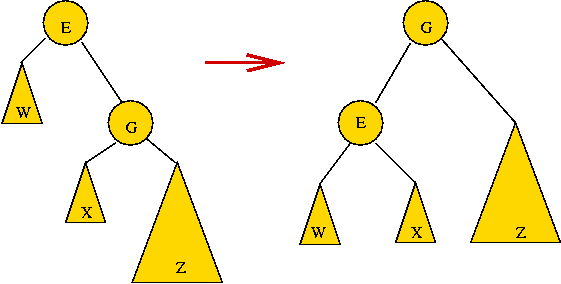
- Example of larger right-height (left-rotate):
- A case where it fails:
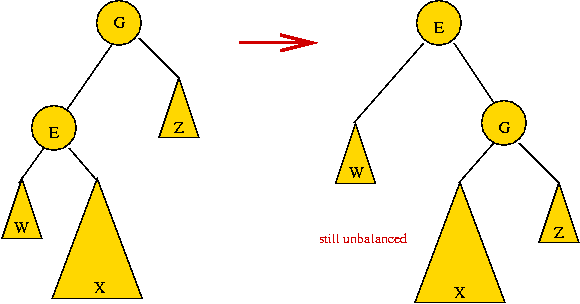
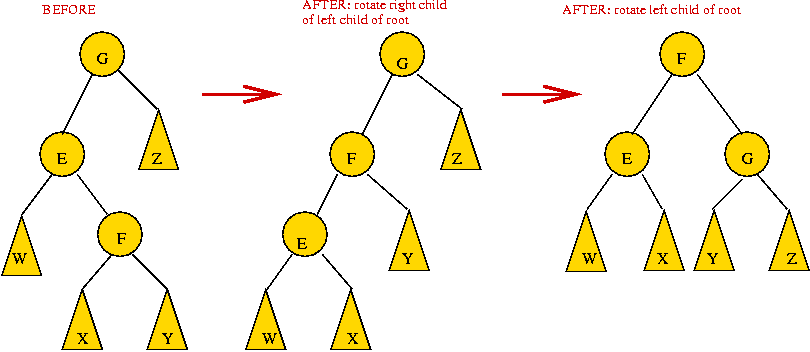
- To restore, use double rotation:
(doubleRotateLeftChild operation)
- Example of double-rotation on the right side:
(doubleRotateRightChild operation)
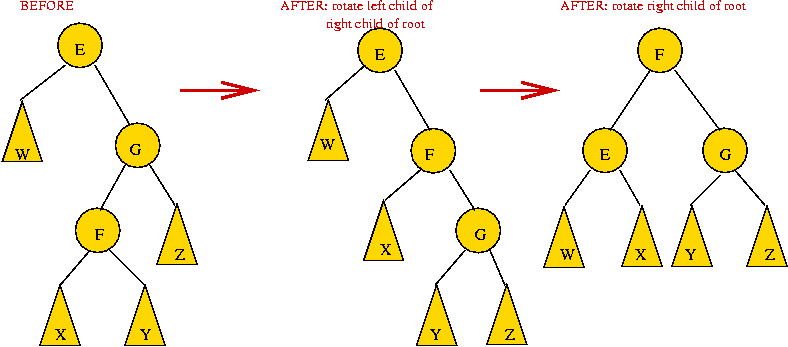
Insertion in an AVL tree:
- Pseudocode:
Algorithm: insert (key, value)
Input: key-value pair
1. if tree is empty
2. create new root with key-value pair;
3. return
4. endif
// Otherwise use recursive insertion
5. root = recursiveInsert (root, key, value)
Algorithm: recursiveInsert (node, key, value)
Input: subtree root (node), key-value pair
// Bottom out of recursion
1. if node is empty
2. create new node with key-value pair and return it;
3. endif
// Otherwise, insert on appropriate side
4. if key < node.key
// First insert.
5. node.left = recursiveInsert (node.left, key, value)
6. // Then, check whether to balance.
7. if height(node.left) - height(node.right) > 1
8. if insertion occurred on left side
9. node = rotateLeftChild (node)
10. else
11. node = doubleRotateLeftChild (node)
12. endif
13. endif
14. else
// Insert on right side
15. node.right = recursiveInsert (node.right, key, value)
// Check balance.
16. if (height(node.right) - height(node.left) > 1
17. if insertion occurred on right side
18. node = rotateRightChild (node)
19. else
20. node = doubleRotateRightChild (node)
21. endif
22. endif
23. endif
24. recomputeHeight (node);
25. return node;
Output: pointer to subtree
- Example:
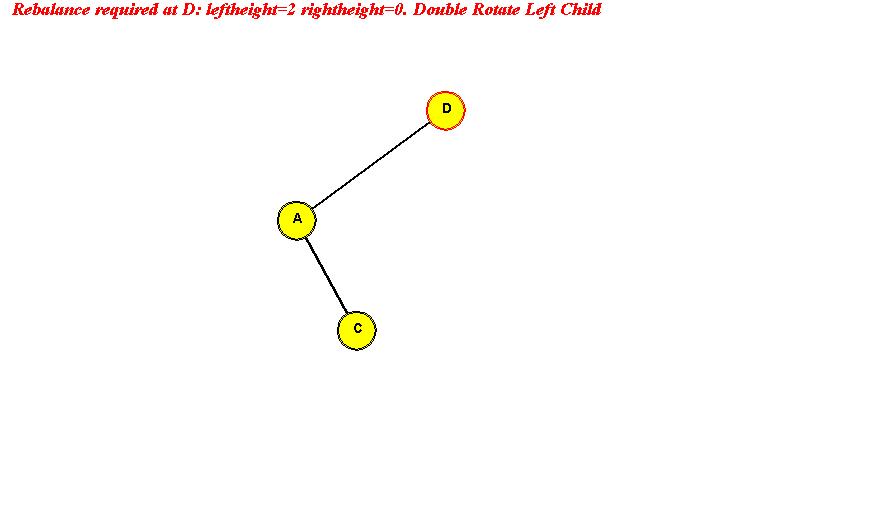
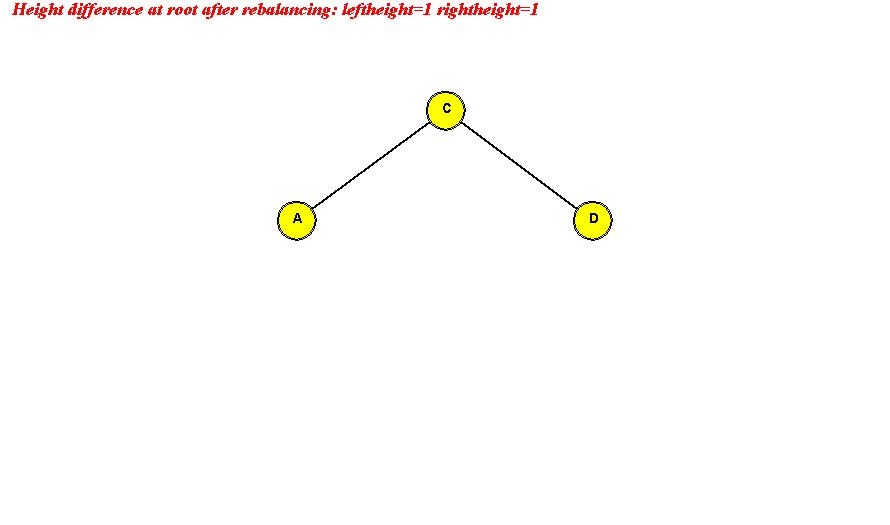
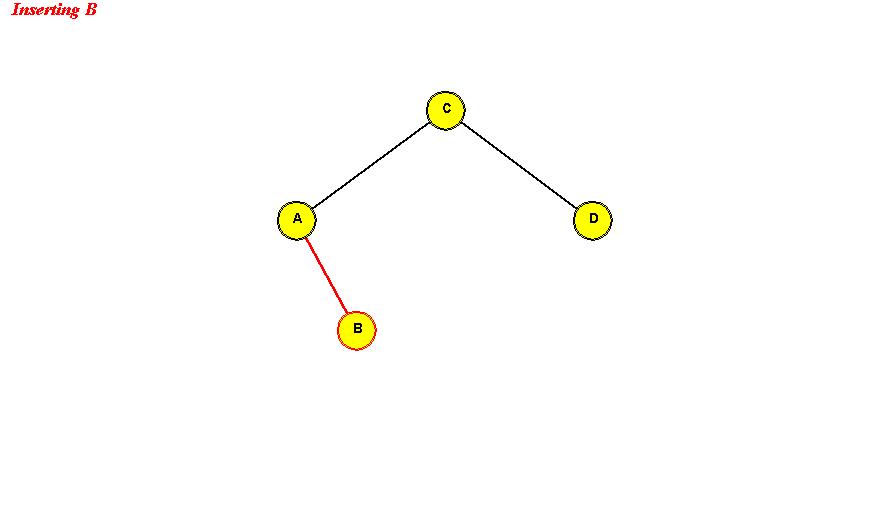
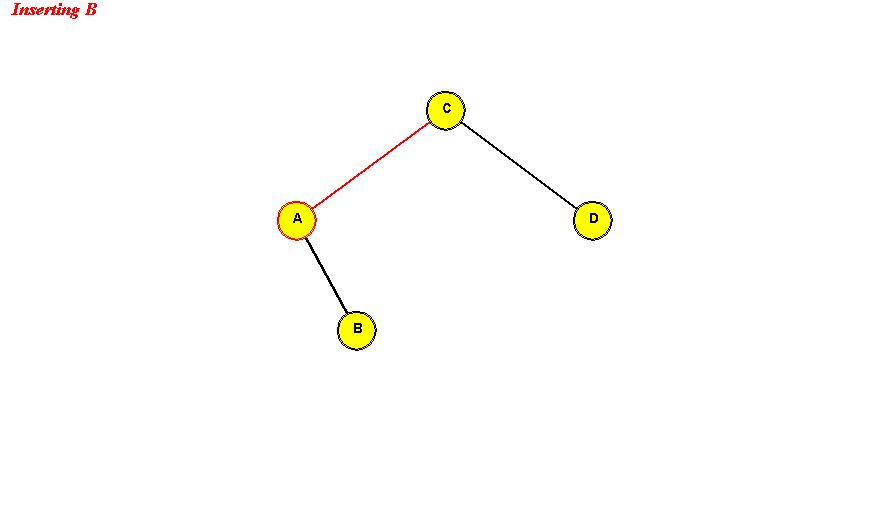
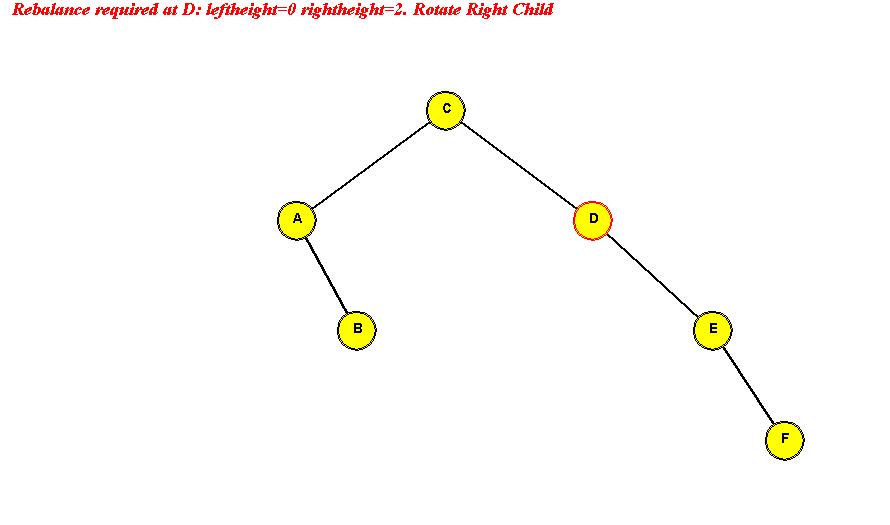
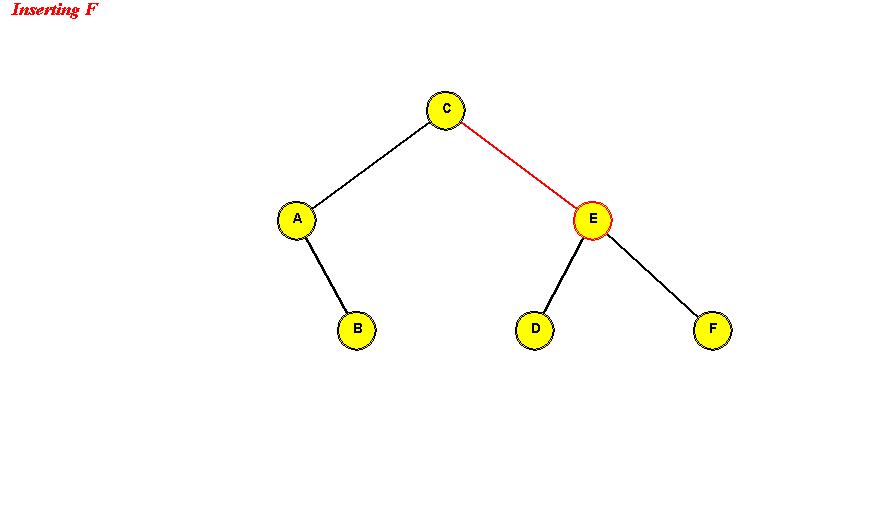
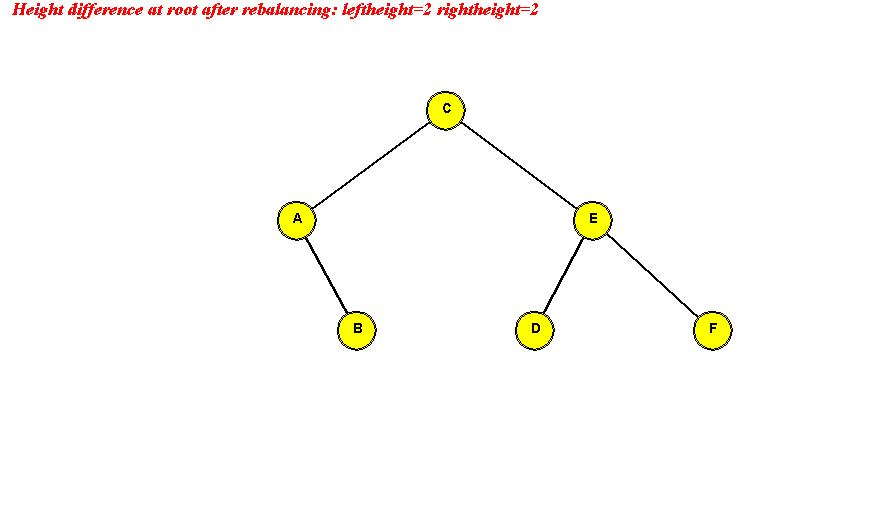
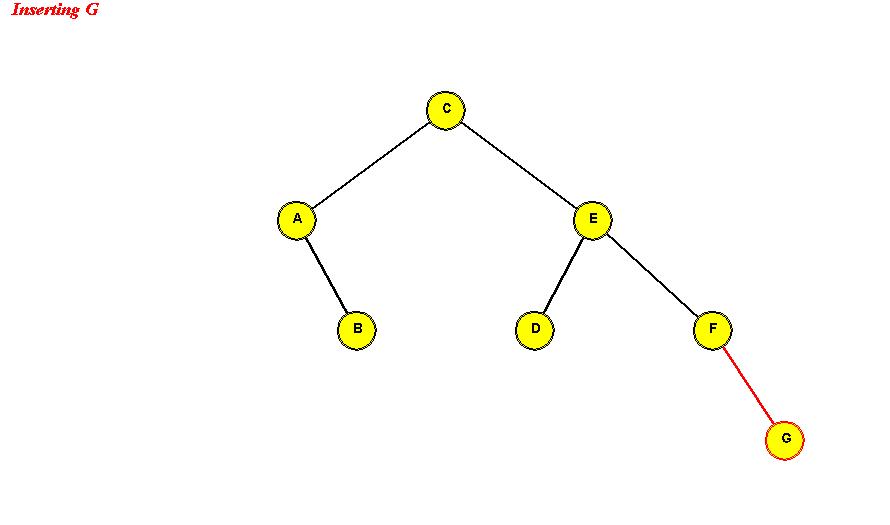
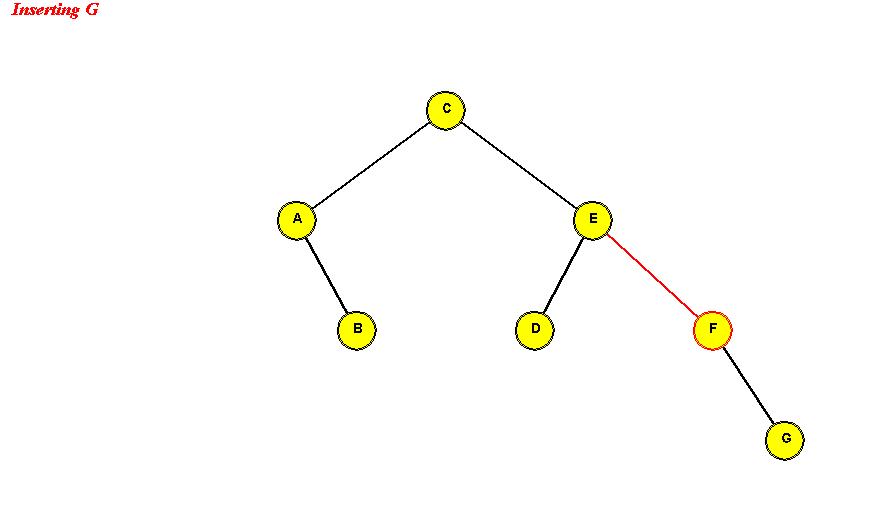
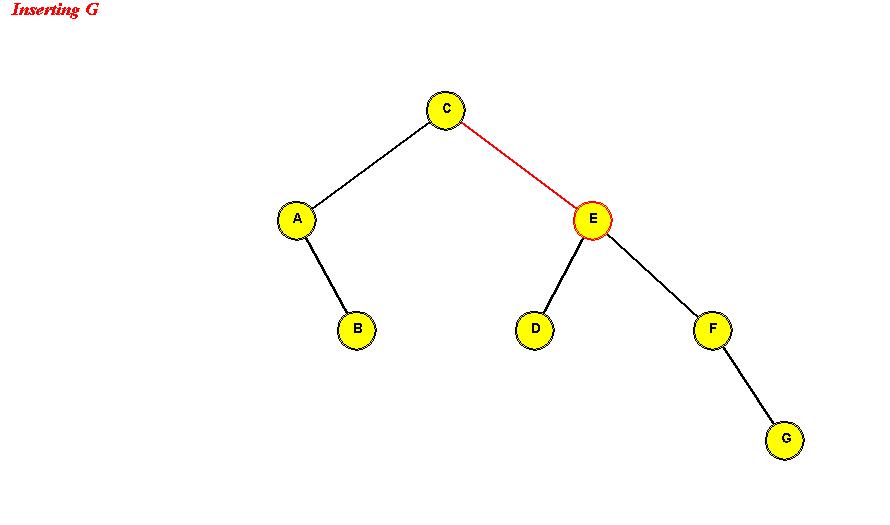
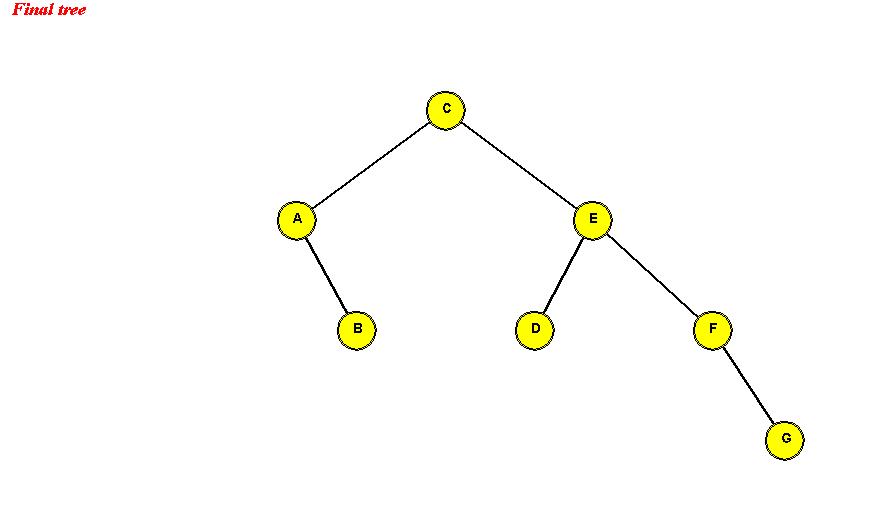
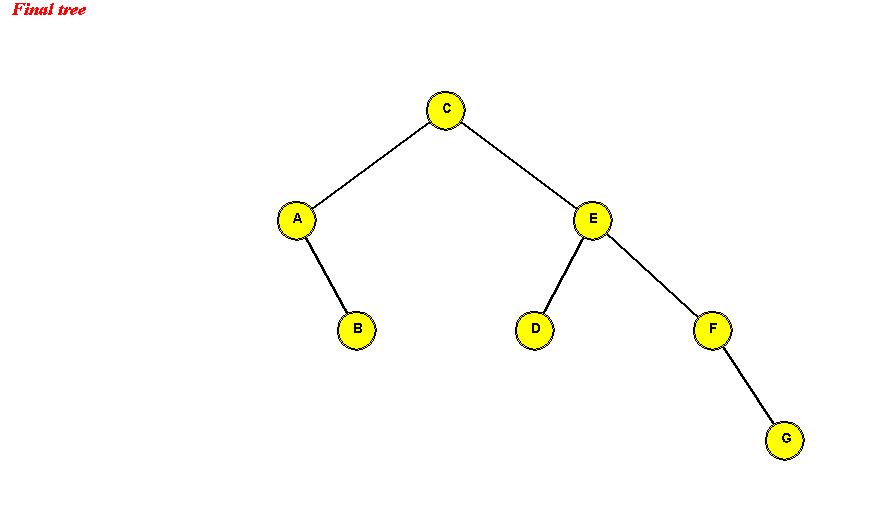
Search: same as in binary search tree.
Deletion: complicated (not covered here).
Analysis:
- Cost of balancing adds no more than O(h), where h
is the worst tree height.
- Because the AVL tree remains balanced, insertion and search
require O(log(n)) time per operation.
- Extra space in each node required for storing height.
=> O(n) extra space.
In practice:
- AVL trees are rarely used because of the difficulty of
deletion, and because of the height-maintenance overhead.
- Options: multiway trees or self-adjusting binary trees.
Multiway trees
About multiway trees:
- Although "multiway" suggests increasing the number of children
per node, we will study a specific kind of multiway tree.
- All leaf nodes will be at the same level.
=> always balanced.
- Associate a number m, called the degree of
the tree.
- Each node except the root must contain at least m-1 keys.
=> important for efficiency.
- Each node can contain at most 2m-1 keys.
- An internal node with k keys contains k+1
pointers.
(Note: k < 2m)
- Leaf nodes do not contain pointers.
- The root must contain at least one key.
In-Class Exercise 3.5:
Suppose a multiway tree of degree m has n keys.
- Argue that the maximum possible height is obtained when each node
except the root has m-1 keys.
- What is the maximum possible height in terms of n?
- What is the maximum possible height when n=109 and m=11?
Searching:
- Start at root node and search recursively.
- Search current node's keys.
If search-key is found, done.
Else, identify child node, search recursively.
If child-pointer is null, key is not in tree.
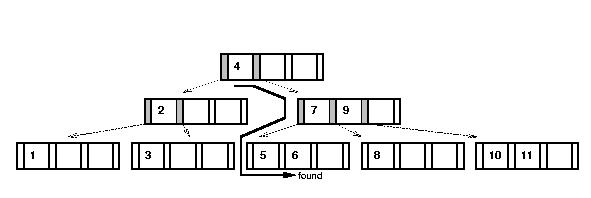
- Example: (m = 2)
Search for `6' in this tree:
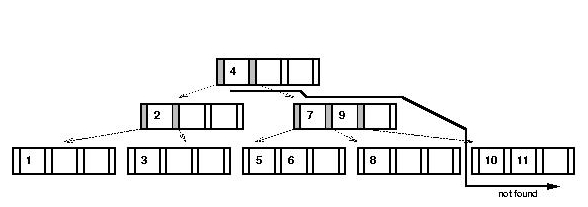
Search for `14':
Insertion:
- We will learn insertion via an example:
- m = 2.
- Key values are integers in this example.
- Insertion order: 1,7,8,10,9,3,2,5,4,6,11.
Note:
- When m=2: at least m-1=1 value per node.
- When m=2: at most 2m-1=3 values per node.
- "Median" value is 2nd value.
Insertion example:
- Initially, create (empty) root node:

- After insertion of `1', `7' and `8':

- Insert `10':
- Root node is full => must split root.
- Median element `7' is bumped up one level (into new root).
- New element is added in appropriate split node.
Step 1: split node:
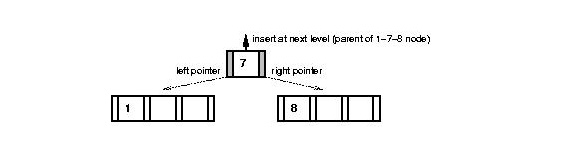
Step 2: Add new key `10':
Step 3: Insert median element `7' with left and right pointers in
level above.
=> in this case, create new root.
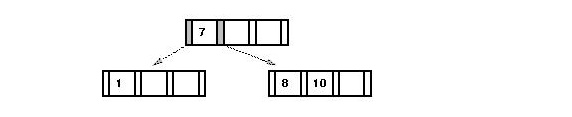
- Key ideas in insertion:
- First, find correct leaf for insertion (wherever search ends).
- If space is available, insert in node.
- Else, split node and "push up" median:
=> insert median element into parent node (with pointers).
- Add new element to left or right split nodes.
- If parent is full, split that ...etc recursively.
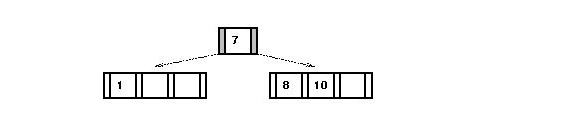
- (Example continued) After insertion of `9', `3' and `2':
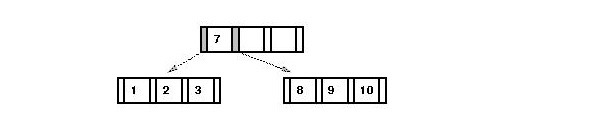
- Insert `5':
- Search for correct leaf => the 1-2-3 node.
- Node is full => split (median is `2').
- Add new key to correct child: the `3' node
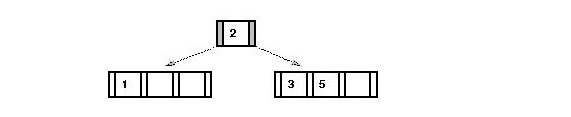
- Insert `2' into parent:
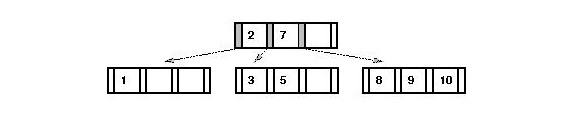
- After insertion of `4' and `6':
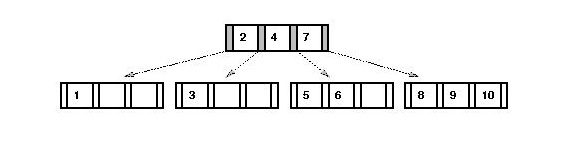
Note:
- The key `7' and everything to the right of it (including
pointers) are shifted to the right.
- The pointer between `2' and `7' is overwritten by `4' and
its pointers.
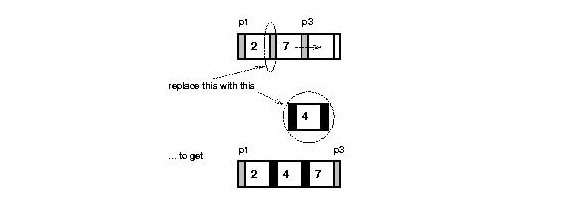
Final tree after inserting `11':
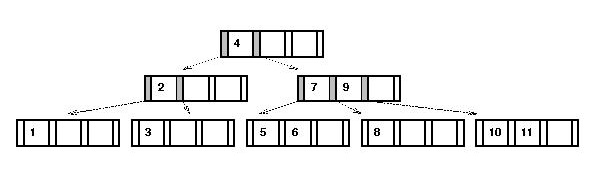
Pseudocode:
- Search:
Algorithm: search (key)
Input: a search key
1. Initialize stack;
2. found = false
3. recursiveSearch (root, key)
4. if found
5. node = stack.pop()
6. Extract value from node;
// For insertions:
7. stack.push (node)
8. return value
9. else
10. return null
11. endif
Output: value corresponding to key, if found.
Algorithm: recursiveSearch (node, key)
Input: tree node, search key
1. Find i such that i-th key in node is smallest key larger than or equal to key.
2. stack.push (node)
3. if found in node
4. found = true
5. return
6. endif
// If we're at a leaf, the key wasn't found.
7. if node is a leaf
8. return
9. endif
// Otherwise, follow pointer down to next level
10. recursiveSearch (node.child[i], key)
- Insertion:
Algorithm: insert (key, value)
Input: key-value pair
1. if tree is empty
2. create new root and add key-value;
3. return
4. endif
// Otherwise, search: stack contains path to leaf.
5. search (key)
6. if found
7. Handle duplicates;
8. return
9. endif
10. recursiveInsert (key, value, null, null)
Algorithm: recursiveInsert (key, value, left, right)
Input: key-value pair, left and right pointers
// First, get the node from the stack.
1. node = stack.pop()
2. if node.numEntries < 2m-1
// Space available.
3. insert in correct position in node, along with left and right pointers.
4. return
5. endif
6. // Otherwise, a split is needed.
7. medianKey = m-th key in node;
8. medianValue = m-th value in node;
9. Create newRightNode;
10. Place keys-values-pointers from 1,...,m-1 in current (left) node.
11. Place keys-values-pointers from m+1,...,2m-1 in newRightNode;
12. Put key and value in appropriate node (node or newRightNode).
13. if node == root
14. createNewRoot (medianKey, medianValue, node, newRightNode)
15. else
16. recursiveInsert (medianKey, medianValue, node, newRightNode)
17. endif
Self-adjusting binary trees
What does "self-adjusting" mean?
- Consider this linked list example:
- The list stores the 26 letters "A" ... "Z".
- For each letter, we store font information (e.g., a
bitmap).
- The list is accessed by an application that needs font
information for printing letters.
- To access a particular letter: start from the front and walk
down the list until the letter is found.
- The time taken to find a letter is the number of letters
before it in the list.
- Suppose we store the letters in the order "A" ... "Z":
- Is this the optimal order?
- What about the order "E" "T" "A" "I" "O" "N" ... ?
In-Class Exercise 3.6:
Suppose the frequency of access for letter "A" is
fA,
the frequency of access for letter "B" is
fB ... etc.
What is the best way to order the list?
- In many applications, the frequencies are not known.
- Yet: successive accesses provide some frequency information.
- Idea: why not re-organize the list with each access?
Self-adjusting linked lists:
- Move-To-Front strategy:
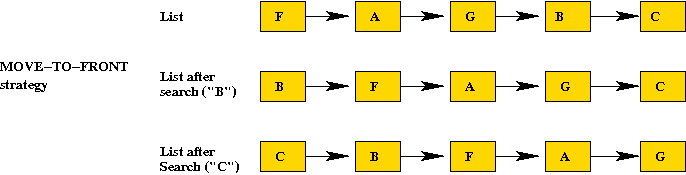
- Whenever an item is accessed, move the item to the front of the list.
- Cost of move: O(1) (constant).
- More frequently-accessed items will tend to be found towards
the front.
- Transpose strategy:
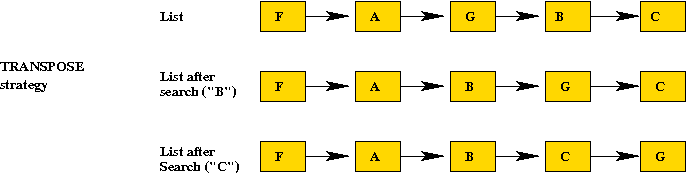
- Whenever an item is accessed, swap it with the one just ahead
of it
(i.e., move it towards the front one place)
- Cost of move: O(1).
- More frequently-accessed items will tend to bubble towards
the front.
In-Class Exercise 3.7:
Consider the following 5-element list with initial order: "A" "B" "C" "D" "E".
- For the Move-To-Front strategy with the access pattern "E" "E" "D" "E" "B" "E",
show the state of the list after each access.
- Do the same for the Transpose strategy with the above
access pattern.
- Create an access pattern that works well for Move-To-Front but
in which Transpose performs badly.
About self-adjusting linked lists:
- It can be shown that Transpose performs better than
Move-To-Front on the average.
- It can be shown that no strategy can results in 50% lower
access costs than Move-To-Front.
- The analysis of self-adjusting linked lists initiated the area of
amortized analysis: analysis over a sequence of accesses (operations).
Self-adjusting binary trees:
- Where should frequently-accessed items be moved?
=> near the root.
- Re-arranging the tree might destroy the "in-order" property?
- To "move" an element towards the root: use rotations.
=> "in-order" property intact.
Using simple rotations:
- A rotation can move a node into its parent's position.
- Goal: use successive rotations to move a node into root position.
- Example:
- However:
- Consider this example:
Tree before rotating "C" to the root:
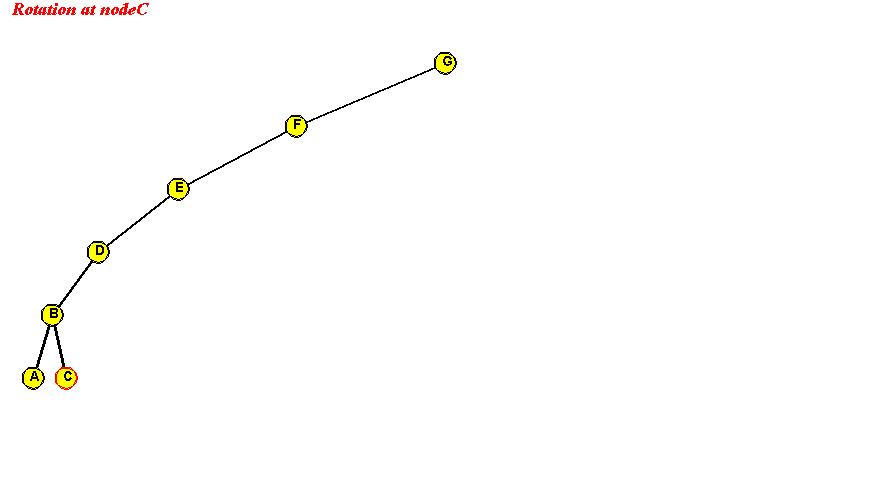
In-Class Exercise 3.8:
Show the intermediate trees obtained in rotating "C" to the root position.
After rotating "C" to the root:
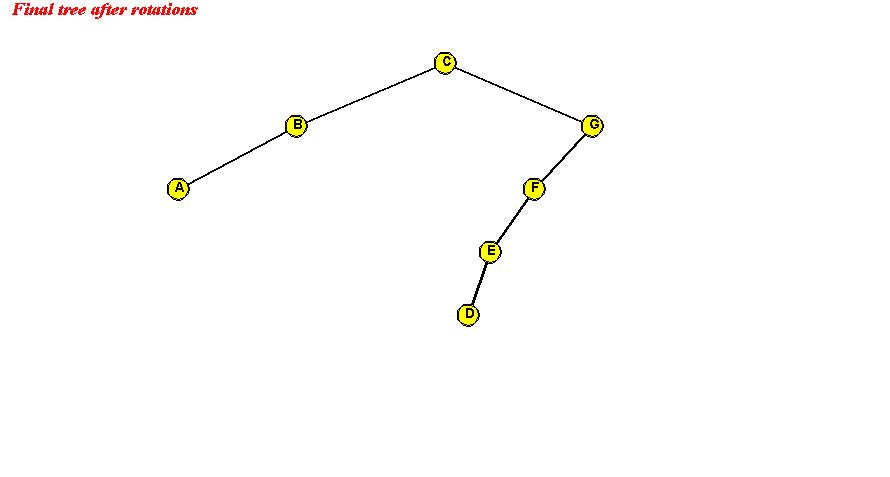
=> simple rotations can push "down one side".
- It can be shown that simple rotations can leave the tree unbalanced.
Using splaystep operations:
- The splaystep is similar to the AVL tree's double
rotation, but is a little more complicated.
- There are 5 cases:
- CASE 1: the target node (to move) is a child of the root.
- CASE 1(a): target node is the root's left child:
rotate node into root position.
=> rotate left child of root (in AVL terms).
- CASE 1(b): target node is the root's right child:
rotate node into root position.
=> rotate right child of root.
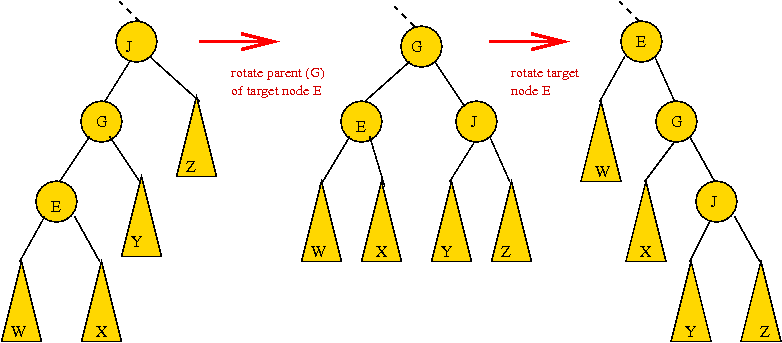
- CASE 2: the target and the target's parent are both left children
- First, rotate the parent into its parent's (grandparent's) position.
This will place the target at its parent's original level.
To do this: rotate the left child of the grandparent.
- Now rotate the target into the next level
This will place the target at its grandparent's original level.
To do this: rotate the left child of the parent
(which is now in the grandparent's old position)
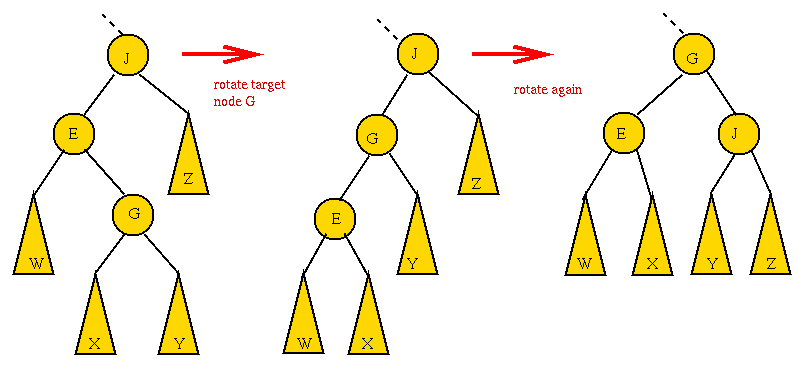
- CASE 3: the target and the target's parent are both right children
- First, rotate the parent into its parent's (grandparent's) position.
=> rotate the right child of the grandparent.
- Now rotate the target into the next level
=> rotate the right child of the parent
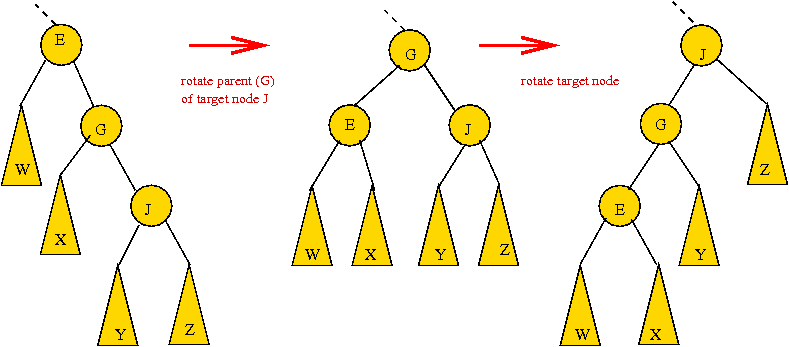
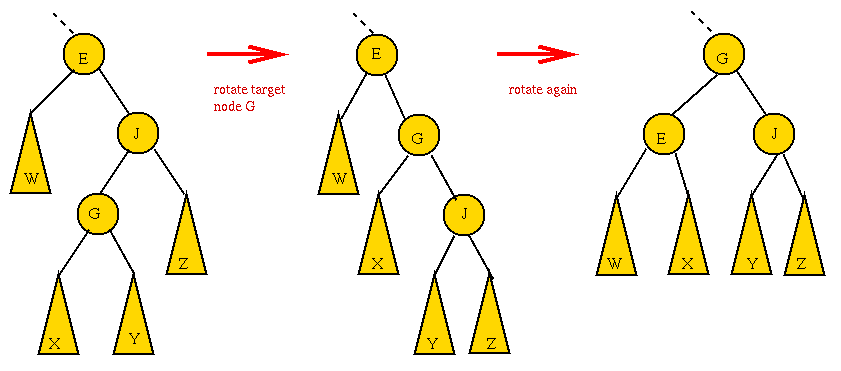
- CASE 4: the target is a right child, the parent is a left child.
- First, rotate the target into the parent's old position.
=> rotate the parent's right child.
- Now the target is a (left) child of the original grandparent.
- Next, rotate the target into the next level.
=> rotate left child of grandparent.
- CASE 5: the target is a left child, the parent is a right child.
- First, rotate the target into the parent's old position.
=> rotate the parent's left child.
- The target is now a (right) child of the original grandparent.
- Next, rotate the target into the next level.
=> rotate right child of grandparent.
- Thus, a target node may move up one or two levels in a
single splaystep operation.
- Through successive splaystep operations a target node can be
moved into the root position.
Search:
- Recursively traverse the tree, comparing with the input key, as in
binary search tree.
- If the key is found, move the target node (where the key was
found) to the root position using splaysteps.
- Pseudocode:
Algorithm: search (key)
Input: a search-key
1. found = false;
2. node = recursiveSearch (root, key)
3. if found
4. Move node to root-position using splaysteps;
5. return value
6. else
7. return null
8. endif
Output: value corresponding to key, if found.
Algorithm: recursiveSearch (node, key)
Input: tree node, search-key
1. if key = node.key
2. found = true
3. return node
4. endif
// Otherwise, traverse further
5. if key < node.key
6. if node.left is null
7. return node
8. else
9. return recursiveSearch (node.left, key)
10. endif
11. else
12. if node.right is null
13. return node
14. else
15. return recursiveSearch (node.right, key)
16. endif
17. endif
Output: pointer to node where found; if not found, pointer to node for insertion.
Insertion:
- Find the appropriate node to insert input key as a child, as in
a binary search tree.
- Once inserted, move the newly created node to the root
position using splaysteps.
- Pseudocode:
Algorithm: insert (key, value)
Input: a key-value pair
1. if tree is empty
2. Create new root and insert key-value pair;
3. return
4. endif
// Otherwise, use search to find appropriate position
5. node = recursiveSearch (root, key)
6. if found
7. Handle duplicates;
8. return
9. endif
// Otherwise, node returned is correct place to insert.
10. Create new tree-node and insert as child of node;
11. Move newly created tree-node to root position using splaysteps;
Deletion:
- Same as in binary search tree.
Analysis:
- It is possible to show that occasionally the tree gets
unbalanced
=> particular operations may take O(n) time.
- Consider a sequence of m operations (among: insert,
search, delete).
- One can show: O(m log(n)) time for the m
operations overall.
- Thus, some operations may take long, but others will be short
=> amortized time is O(log(n)) per operation.
- Note: amortized O(log(n) time is stronger than
average O(log(n) time.
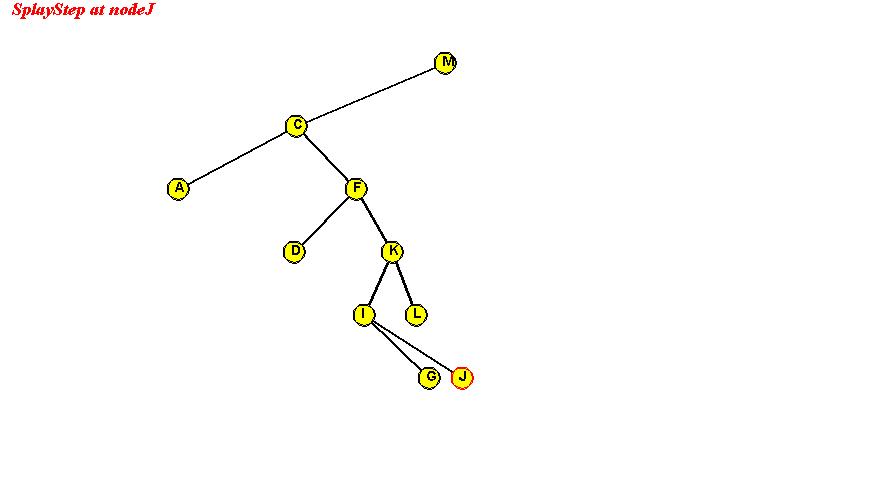
In-Class Exercise 3.9:
Show the intermediate trees and final tree after "J" is moved into the
root position using splaysteps. In each case, identify which "CASE" is
used.