Sequence Alignment
What is Alignment?
Let's distinguish between two uses of "alignment":
Types of two-sequence alignments:
- Global alignment:
- Input: treat the two sequences as potentially equivalent.
- Goal: identify conserved regions and differences.
- Algorithm: Needleman-Wunsch dynamic programming
- Applications:
- Comparing two genes with same function (in human vs. mouse).
- Comparing two proteins with similar function.
- Local alignment:
- Input: The two sequences may or may not be related.
- Goal: see whether a substring in one sequence aligns well
with a substring in the other.
- Algorithm: Smith-Waterman dynamic programming
- Applications:
- Searching for local similarities in large sequences (e.g.,
newly sequenced genomes).
- Looking for conserved domains or motifs in two proteins.
- Semi-global alignment:
- Input: two sequences, one short and one long.
- Goal: is the short one a part of the long one?
- Algorithm: modification of Smith-Waterman.
- Applications:
- Given a DNA fragment (with possible error), look for it in
the genome.
- Look for a well-known domain in a newly-sequenced protein.
- Suffix-prefix alignment:
- Input: two sequences (usually DNA)
- Goal: is the prefix of one the suffix of the other?
- Algorithm: modification of Smith-Waterman.
- Applications:
- Heuristic alignment:
- Input: two sequences.
- Goal: See if two sequences are "similar" or candidates for alignment.
- Algorithms: BLAST, FASTA (and others)
- Applications:
- Search in large databases.
Difference between keyword-search and alignment:
- Keyword search:
- Keyword search is exact matching.
- Can be done quickly (straightforward scan).
- Used in Entrez (for example)
- Alignment:
- Non-exact, scored matching.
- Takes much more time.
- Used in tools like BLAST2, CLUSTALW.
Problems from a biologist's point of view:
- "I have just sequenced a DNA fragment"
=> you have a piece of unknown DNA.
- Run a BLAST search (which uses the BLAST algorithm).
=> result: other DNA fragments (or genomes) that contain
similar stretches.
- Once you have candidates, run a more careful alignment among them.
=> local alignment or semi-global alignment.
- "I've located a gene using a gene-finding algorithm"
=> you have the gene sequence fairly well determined.
- Run BLAST to locate similar genes.
- Run a global alignment to see differences.
- Alternatively, identify potential proteins via a protein database.
- "I'm confirming a sequencing experiment first done by
someone else"
=> do a global alignment.
- "I've sequenced a new protein"
=> BLAST search (on proteins) and then global alignment on results.
- "I've found a new domain or motif"
=> BLAST to locate proteins of interest, then semi-global alignment.
Global Alignment - The Needleman-Wunsch Algorithm
The alignment problem in Computer Science terms:
- Given two strings and the scoring rules, find the optimal alignment.
- Define scoring rules for evaluating a particular alignment:
- Perfectly matched letters get a high score.
- Matches between related letters get a modest score.
- Matches with gaps get a low score.
- Problem components:
- An alphabet
e.g., { A, C, G, T } (DNA
e.g., { M, A, L, ..., } (protein)
- Two input strings, e.g.,
- Match and gap scores, e.g.,
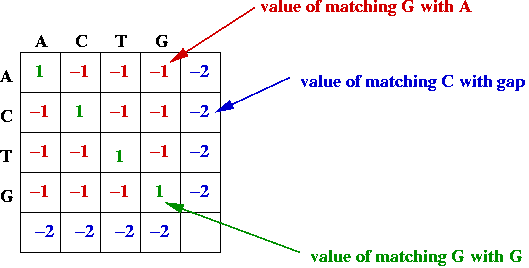
- Goal: find the alignment with the best (largest) value.
- Potential asymmetry:
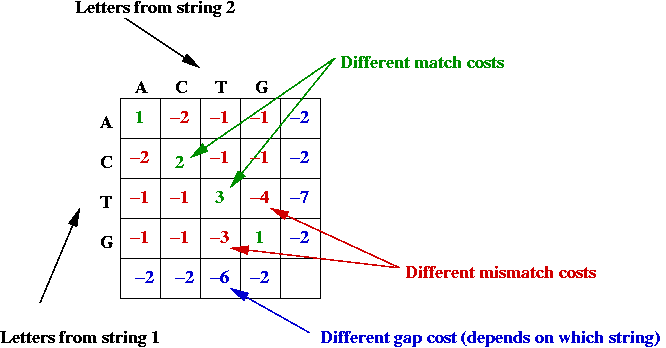
- Some letter-alignments may be more favored.
- Some gap costs are different.
- Example:
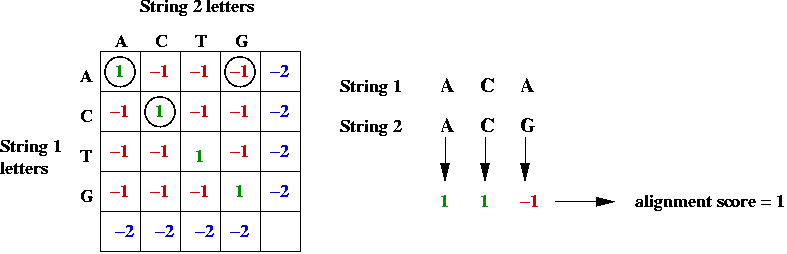
- Example:
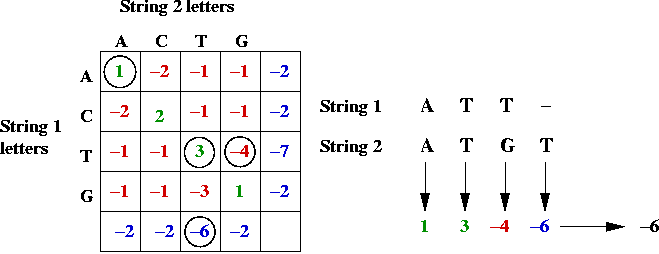
Key ideas in solution:
- First, the alignment problem can be expressed as a
graph problem:
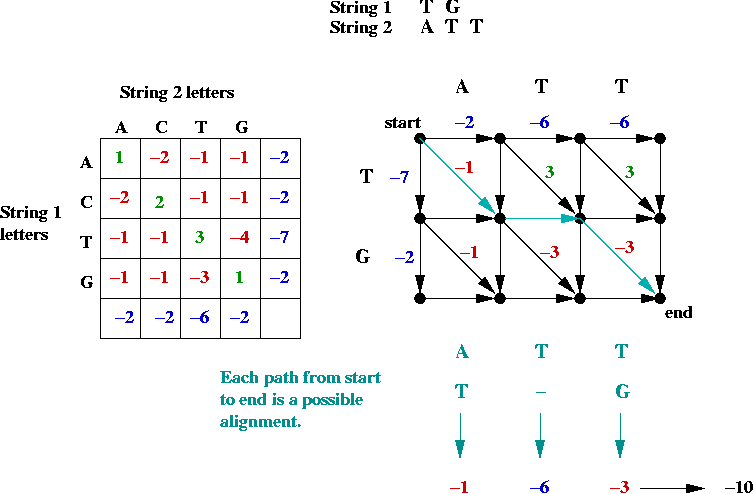
- The diagonal edges correspond to character matches
(whether identical or not).
- Each down edge corresponds to a gap in string 2.
- Each across edge corresponds to a gap in string 1.
- Goal: find the longest (max value) path from top-left to bottom-right.
=> longest-path problem in Directed Acyclic Graph.
- Can be solved in O(mn) time (using topological sort)
(m = length of string1, n = length of string2).
- Suppose we label the vertices (i, j) where
i is the row, and j is the column.
- The best path to an intermediate node is via one of its
neighbors: NORTH, WEST or NORTHWEST.
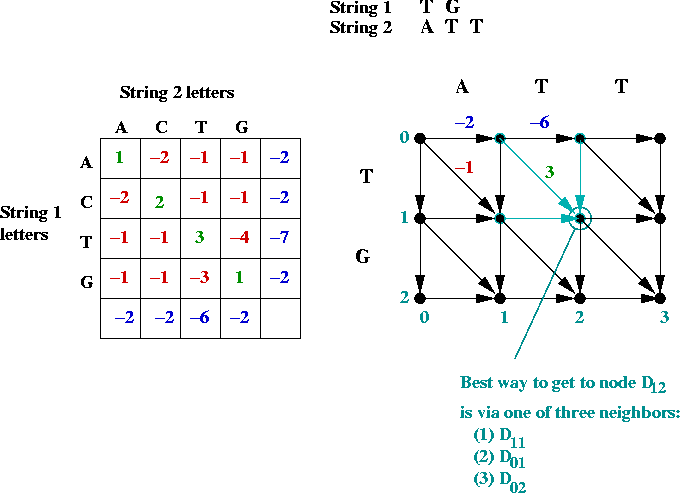
- Dynamic programming approach:
- Building an actual graph (adjacency matrix etc) is unnecessary.
- Let Di,j
= value of best path to node (i,j) from (0, 0).
= score of optimal match of first i chars in string 1
to first j chars in string 2.
- Define (for clarity)
| Ci-1,j-1 |
= |
Di-1,j-1 + exact-match-score |
| Ci-1,j |
= |
Di-1,j + string1-gap-score |
| Ci,j-1 |
= |
Di,j-1 + string2-gap-score |
- Thus,
| Di,j |
= |
max (Ci-1,j-1, Ci-1,j, Ci,j-1) |
| |
= |
max (Di-1,j-1 + exact-match-score,
Di-1,j + string1-gap-score,
Di,j-1 + string2-gap-score) |
- Initial conditions:
- D0,0 = 0
- Di,0 = Di-1,0 + gap-score for
i-th char in string 1.
- D0,j = D0,j-1 + gap-score for
j-th char in string 2.
Implementation:
- Pseudocode:
Algorithm: align (s1, s2)
Input: string s1 of length m, string s2 of length n
1. Initialize matrix D properly;
// Build the matrix D row by row.
2. for i=1 to m
3. for j=1 to n
// Initialize max to the first of the three terms (NORTH).
4. max = D[i-1][j] + gapScore2 (s2[j-1])
// See if the second term is larger (WEST).
5. if max < D[i][j-1] + gapScore1 (s1[i-1])
6. max = D[i][j-1] + gapScore1 (s2[i-1])
7. endif
// See if the third term is the largest (NORTHWEST).
8. if max < D[i-1][j-1] + matchScore (s1[i-1], s2[j-1])
9. max = D[i-1][j-1] + matchScore (s1[i-1], s2[j-1])
10. endif
11. D[i][j] = max
12. endfor
13. endfor
// Return the optimal value in bottom-right corner.
14. return D[m][n]
Output: value of optimal alignment
- Explanation:
- The 2D array D[i][j] stores the Di,j values.
- The method matchScore returns the value in matching
two characters.
- The method gapScore1 returns the value of matching a
particular character in string 1 with a gap.
(gapScore2 is similarly defined).
- Note: D[i][0] and D[0][j] represent
initial conditions.
- Note: there is one more row than the length of string 1.
(likewise for string 2).
- Computing the actual alignment:
- A separate 2D array tracks which term contributed to the
maximum for each (i, j).
- After computing all of D, traceback and obtain path (alignment).
In-Class Exercise:
(Solution)
Download this template and
implement the above algorithm. Gap and match costs are given.
Analysis:
- The double for-loop tells the story: O(mn) to compute Dm,n.
- Note: computing the actual alignment requires tracing back:
O(m + n) time (length of a path).
- Space required: O(mn).
An improvement (in space):
- Genes are often longer than 10,000 bases (letters) long
=> space required is prohibitive.
- First, note that we only need successive rows in computing D
=> space requirement can be reduced to O(n).
- However, O(mn) space is still required to construct
the actual alignment.
- A different approach:
- Consider the "middle" character in string 1
=> the character at position m / 2.
- In the optimal alignment, this character will either align
with some j-th character in string 1, or a gap.
=> we can try all possible j values.
- To try these alignments, compute the m/2-th row (in
O(mn) time).
- Output the optimal alignment found.
- Recurse on either side of the optimal alignment.
- It is possible to show: O(mn) time and O(n) space.
Local Alignment - The Smith-Waterman Algorithm
Consider a global alignment example:
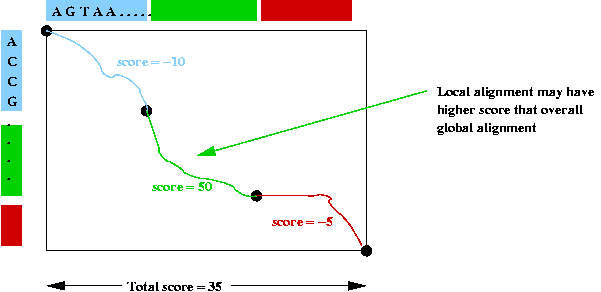
- An alignment is forced across the whole table.
=> each position is scored.
- However, the score in one particular section may be higher
=> local alignments may have higher scores.
- Goal in local alignment: find best possible local alignment.
Two key modifications to global alignment algorithm:
- Starting new alignments:
- As with global, start at top left corner.
- However, if an alignment gets too expensive, discard it and
start a new one.
- Look for best local alignment:
- As with global, fill all matrix entries.
- However, do not count on bottom-right as starting point
=> search entire matrix for best "bottom-right corner of
local alignment"
To achieve the first part:
- Decide when a local alignment should be abandoned (i.e., when a
new one should start).
=> Typically, when score goes below zero.
- Modify recurrence to avoid below-zero scores:
| Di,j |
= |
max (0, Ci-1,j-1, Ci-1,j, Ci,j-1) |
- If 0 is the maximum score at (i, j)
=> a new alignment is started.
- Record (i, j) values where new alignments start.
To achieve the second part:
- Search for Di,j with highest score.
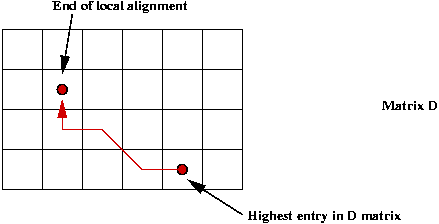
- Work backwards from this point.
Scoring - the PAM Approach
What is PAM?
- PAM = Point Accepted Mutations.
- A theory for assigning scores to substitutions (mutations) in proteins.
Consider a group of related proteins and a particular position:
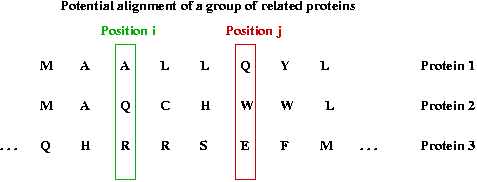
- Suppose the proteins are listed in evolutionary order and aligned.
- We'll use a, b, c], ... to denote amino acids.
- A mutation from a to b can occur in one step or many.
- Let Mab = Pr[an a -> b mutation occurs] in
some position.
- Let Maa = Pr[no mutation occurs].
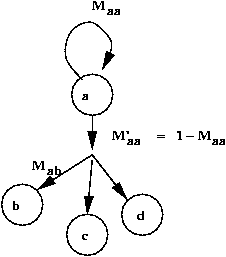
- Let pa = Pr[residue a occurs].
Scoring intuition:
- Consider scoring the substitution a to b.
- Want a high score if Mab is high
=> because of high a -> b mutations.
- Want a low score if pb is high
=> because high occurence of b explains occurence of
b (as opposed to mutation).
- Solution: let score be proportional to Mab / pb
PAM scoring:
- Consider mutations in two positions: a -> b and c -> d.
- Probability of both occuring is proportional to product:
(Mab / pb) * (Mcd / pd)
- But algorithm requires scores to be additive (for decomposability).
- Take logarithms:
score =
log (Mab / pb) + log (Mcd / pd)
Evolutionary distance in PAM scoring:
- In comparing a -> b in two proteins:
- One possibility: the two proteins are phylogenetically
adjacent
=> direct a -> b mutation.
- Another possibility: several intermediate mutations occured:
e.g., a -> e -> f -> b. (evolutionary distance = 3)
e.g., c -> g -> d. (evolutionary distance = 2)
- Goal: design scoring for a particular distance k.
- What do we want reflected in the score?
- Let Mabk = Pr[a -> b in k steps].
- Compute Mabk for each a,
b.
- Score for a -> b is:
log (Mabk / pb)
- Thus, in PAM-250 (a popular one), k = 250.
Note:
- We have only sketched some of the theory: a more rigorous
explanation requires background in Markov chain theory.
- Usually, it is desirable to adjust the "rate of overall
mutation" in the theory.
- Let M'aa = Pr[mutation from a]
- Let Maa = 1 - M'aa
- Adjust the ratio M'aa / Maa
- Typical value: 1/100
=> one mutation in every 100 amino acids.
How BLAST Works
Key ideas in BLAST (e.g, protein) searches:
- BLAST computes "similarity", not "alignment".
- Given two protein sequences:
- Find all substrings of length k (typical: k = 4) that occur in both strings.
- Build score based on matches.
- Extend substrings to see if match score can be increased.
- Compute total score when no more extensions are possible.
- Compute BLAST score against all proteins in database.
- Rank order search results by score.