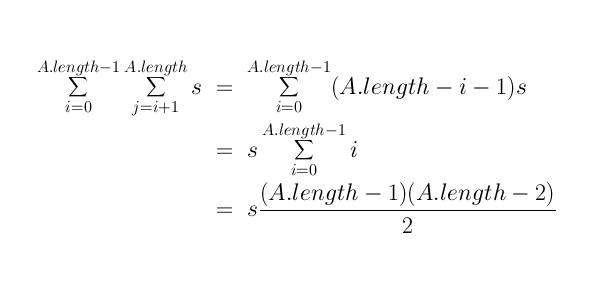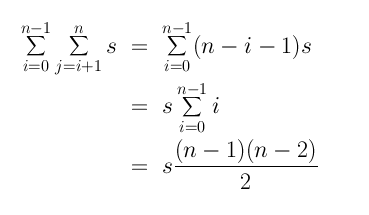Module 1: Introduction
A simple problem and some solutions
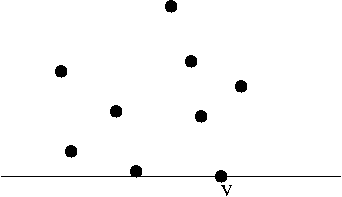
Consider the largest distance problem:
- Input: a set of points on the place (x and y values for each point).
- Output: the distance between the two points that are furthest apart.
- Sample application: enclosure/aperture design.
In-Class Exercise 1:
In this exercise you will write code to find the distance
between the two furthest points among a set of points:
Now consider this algorithm:
- First, compute the convex hull of the set of points.
- Then, scan the hull and find antipodal pairs.
- Compute the distances between antipodal pairs.
- Report the largest such distance.
Let's take this one step at a time:
- What is a convex hull?
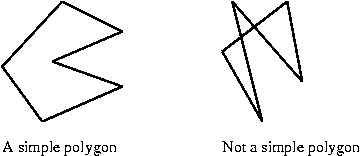
- First: a (simple) polygon is an ordered
set of edges such that successive edges and only
successive edges share a single endpoint.
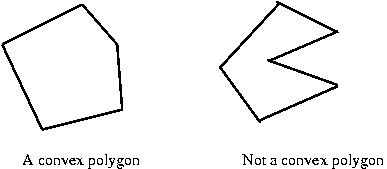
- Second: a polygon is convex if no internal
angle is larger than 180 degrees.
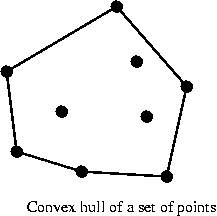
- Finally: for a set of points, the convex hull is the
smallest convex polygon completely enclosing the points.
- Using the Graham-Scan algorithm to compute the convex
hull:
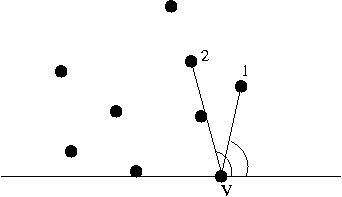
- Find distances between antipodal pairs:
- For a given vertex, its antipodals are
those points that lie on parallel lines that don't cross
the hull.
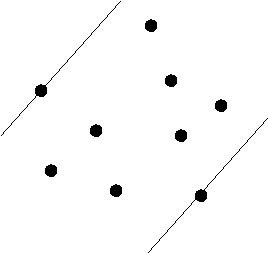
- Key observation: the two farthest points in the set must
be antipodal pairs on the hull.
- To find these distances, compute distances to each edge:
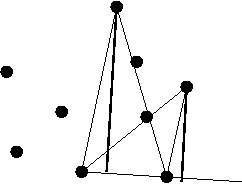
- Another key observation: antipodal pairs can be
found in a single sweep
=> your clockwise neighbor's antipodal is farther along than
your antipodal.
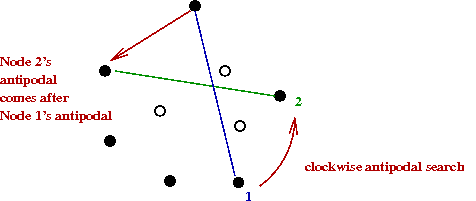
Now, let's take a first look at the code:
- The AntiPodal Algorithm:
(source file):
public class AntiPodalAlgorithm {
static double distance (Pointd p, Pointd q)
{
// Return the Euclidean distance between the two points.
}
static double findMaxDistance3 (Pointd[] points, int a, int b, int c)
{
// Compute the distance between each of ab, ac and bc,
// and return the largest.
}
boolean turnComplete = false;
int nextCounterClockwise (Pointd[] points, int i)
{
// Find the next point in the list going counterclockwise,
// that is, in increasing order. Go back to zero if needed.
// Return the array index.
}
int prevCounterClockwise (Pointd[] points, int i)
{
// Similar.
}
int findAntiPodalIndex (Pointd[] hullPoints, int currentIndex, int startAntiPodalIndex)
{
// Given a convex polygon, an index into the vertex array (a particular vertex),
// find it's antipodal vertex, the one farthest away. Start the search from
// a specified vertex, the "startAntiPodalIndex"
}
public double findLargestDistance (Pointd[] points)
{
// 1. Compute the convex hull:
Hull hull = new Hull (points);
// 2. Extract the hull points:
Pointd[] hullPoints = hull.getPoints();
// 3. If it's exactly three points, we have a method just for that:
if (hullPoints.length == 3)
return findMaxDistance3 (hullPoints, 0, 1, 2);
// Otherwise, we start an antipodal scan.
boolean over = false;
// 4. Start the scan at vertex 0, using the edge ending at 0:
int currentIndex = 0;
int prevIndex = prevCounterClockwise (hullPoints, currentIndex);
// 5. Find the antipodal vertex for edge (n-1,0):
int antiPodalIndex = findAntiPodalIndex (hullPoints, currentIndex, 1);
// 6. Set the current largest distance:
double maxDist = findMaxDistance3 (hullPoints, currentIndex, prevIndex, antiPodalIndex);
// We'll stop once we've gone around and come back to vertex 0.
double dist = 0;
turnComplete = false;
// 7. While the turn is not complete:
while (! over) {
// 7.1 Find the next edge:
prevIndex = currentIndex;
currentIndex = nextCounterClockwise (hullPoints, currentIndex);
// 7.2 Get its antipodal vertex:
antiPodalIndex = findAntiPodalIndex (hullPoints, currentIndex, antiPodalIndex);
// 7.3 Compute the distance:
dist = findMaxDistance3 (hullPoints, currentIndex, prevIndex, antiPodalIndex);
// 7.4 Record maximum:
if (dist > maxDist)
maxDist = dist;
// 7.5 Check whether turn is complete:
if (turnComplete)
over = true;
} // end-while
// 8. Return largest distance found.
return maxDist;
}
} // End-class
- Computing the convex hull:
import java.util.*;
public class Hull {
// Maintain hull points internally:
private Pointd[] hull;
// The data set is given to the constructor.
public Hull (Pointd[] points)
{
Pointd[] vertices;
int i, n;
// Record the number of vertices:
n = points.length;
// 1. Make a copy of the vertices because we'll need to sort:
vertices = new Pointd[n];
System.arraycopy (points, 0, vertices, 0, n);
// 2. Find the rightmost, lowest point (it's on the hull).
int low = findLowest (vertices);
// 3. Put that in the first position and sort the rest by
// angle made from the horizontal line through "low".
swap (vertices, 0, low);
HullSortComparator comp = new HullSortComparator (vertices[0]);
Arrays.sort (vertices, 1, vertices.length-1, comp);
// 4. Remove collinear points:
n = removeCollinearPoints (vertices);
// 5. Now compute the hull.
hull = grahamScan (vertices, n);
}
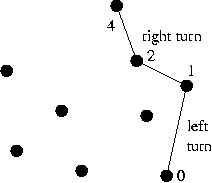
Pointd[] grahamScan (Pointd[] p, int numPoints)
{
// 1. Create a stack and initialize with first two points:
HullStack hstack = new HullStack (numPoints);
hstack.push (p[0]);
hstack.push (p[1]);
// 2. Start scanning points.
int i = 2;
// 3. While scan not complete:
while (i < numPoints)
{
// 3.1 If the current point is on the hull, push next one.
// We know a point is potentially on the hull if the
// the angle is convex (a left turn).
if ( hstack.isHull (p[i]) )
hstack.push (p[i++]);
// Else remove it.
else
hstack.pop ();
// NOTE: the isHull() method looks for "left" and "right" turns.
}
// 4. Return all points still on the stack.
return hstack.hullArray();
}
private int findLowest (Pointd[] v)
{
// 1. Scan through points:
// 1.1 If y-value is lower, the point is lower. If the y-values
// are the same, check that the x value is further to the right:
// 2. Return lowest point found:
}
int removeCollinearPoints (Pointd[] p)
{
// Not shown
}
void swap (Pointd[] data, int i, int j)
{
// Not shown
}
}
Next, consider this idea:
- Suppose experimentation reveals that the hull points are only a
small subset of all the points.
For example, we compute the number of hull points for the
following data sizes (randomly generated):
| # of points | # hull points |
| 10 | 6 |
| 100 | 13 |
| 1000 | 18 |
| 10000 | 25 |
- This suggests computing the hull and then doing an all-pairs
distance computation:
(source file):
public class HullAlgorithm {
static double distance (Pointd p, Pointd q)
{
// Return the distance between points p and q.
}
public double findLargest (Pointd[] points)
{
// For each pair of points: compute the distance, recording
// the largest such distance:
}
public double findLargestDistance (Pointd[] points)
{
// 1. Find the convex hull:
Hull hull = new Hull (points);
// 2. Extract the points:
Pointd[] hullPoints = hull.getPoints();
// 3. Compute an all-pairs largest-distance:
return findLargest (hullPoints);
}
}
Note:
- Fact: the AntiPodal algorithm is provably fast (fastest
possible, in a worst-case sense).
- Fact: the Hull algorithm is experimentally fast, but not
provably so.
- Fact: it is possible to create pathological test data that makes the Hull
algorithm perform badly.
In-Class Exercise 2:
What is this pathological test data? Give an example.
Summary:
- It is possible to design much faster algorithms using
insight into problem structure.
- A fast algorithm may be slow for small data sets, and might
require some setup overhead.
- A fast algorithm may be quite complicated, and use complicated
data structures.
- Some experimentation with typical data sets may reveal simpler
approaches that are as effective as the provably-fast algorithms.
Improving a program's speed
Consider the following problem:
- Input: an array of numbers.
- Output: the two numbers whose absolute difference is largest,
and the absolute difference.
As a first attempt to solve this problem, consider
(source file):
static void algorithm1 (double[] A)
{
// 1. Set the initial maximum to the difference between the first two:
double max = Math.abs (A[0] - A[1]);
// 2. Record the actual values:
double x = A[0], y = A[1];
// 3. Now compare each pair of numbers:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
// 3.1 For each such pair, see if it's difference is larger
// than the current maximum.
double diff = Math.abs (A[i] - A[j]);
if (diff > max) {
// 3.1.1 If so, record the new maximum and the values
// that achieved it.
max = diff;
x = A[i];
y = A[j];
}
} // inner-for
} // outer-for
// 4. Output:
System.out.println ("Algorithm 1: the numbers: " + x + "," + y
+ " difference=" + max);
}
Here are some timings for different array sizes (in milliseconds):
| Array size | execution time |
| 1000 | 84 |
| 2000 | 258 |
| 3000 | 554 |
| 4000 | 985 |
| 5000 | 1551 |
| 6000 | 2228 |
| 7000 | 3031 |
| 8000 | 3962 |
| 9000 | 5020 |
| 10000 | 6247 |
How could we improve this program?
In-Class Exercise 3:
In what other ways can the original Java program be improved?
Instead, let's consider some algorithmic improvements:
- Algorithm 2:
(source file)
static void algorithm2 (double[] A)
{
// 1. Sort the array:
Arrays.sort (A);
// 2. The smallest is first, the largest last:
double diff = A[A.length-1] - A[0];
// 3. Output:
System.out.println ("Algorithm 2: the numbers: " + A[0] + "," + A[A.length-1]
+ " difference=" + diff);
}
- Algorithm 3:
(source file)
static void algorithm3 (double[] A)
{
// 1. Initialize min and max:
double min = A[0];
double max = A[0];
// 2. Scan through array finding the latest min and max:
for (int i=1; i < A.length; i++){
if (A[i] < min)
min = A[i];
else if (A[i] > max)
max = A[i];
}
// 3. Output:
double diff = max - min;
System.out.println ("Algorithm 3: the numbers: " + min + "," + max
+ " difference=" + diff);
}
In-Class Exercise 4:
Why are algorithms 2 and 3 faster?
In-Class Exercise 5:
Take your code for Exercise 1, and count the number of times "distance"
is computed. For n points, how many times is distance computed?
Course outline
What this course is about:
- Part of the science in computer science.
- Algorithm analysis: both for execution time and other
resources (like memory).
- Problem-solving techniques.
- Exposure to classic computer science problems and techniques.
- Exposure to useful data structures.
- Exposure to important types of combinatorial objects (graphs,
strings, geometry).
- Exposure to discrete optimization problems.
- Performance monitoring and code tuning.
- Writing clean, efficient code.
In addition, you will:
- Learn to think about problems and algorithms independent of code.
=> Algorithmic thinking
- Improve your analytic skills.
- Improve your programming skills:
- More challenging debugging (e.g., "tree" code).
- Reusable code.
- Think at the right level of detail.
- Increase your ability to learn new material by yourself.
Key principles:
- Insight: Analysis of problem structure.
- Data organization: possibly sort the data, use an
efficient data structure.
- Divide and conquer:
- Breakdown the problem in the "right" way
- Solve smaller problems first.
- Put together solution from sub-solutions.
- Simple, effective code:
- Exploit the power of recursion.
- Reusable data structures.
- Simple, clear interfaces to data structures, and subproblem algorithms.
- Statistics: exploit statistical characteristics in data.
Algorithms in the context of the rest of computer science:
- The science of algorithms is a key computer science technology.
- Hard problems have been analysed and clever algorithms have
made some computations routinely fast.
Example: sorting
- A large class of (but not all) algorithms go hand-in-hand with
data structures.
These data structures tend to be used again and again.
- Often, some applications demand slight modifications in data structures.
(So, it's not enough to use a package).
- Algorithmic insight is a key skill.
- Algorithm analysis is an integral part of many other courses.
Algorithms
What is an algorithm?
- An algorithm is NOT a program.
- An algorithm is: the key ideas underlying a program that remain the same
no matter what language or machine is used.
- An algorithm sometimes consists of sub-algorithms
e.g., finding the convex hull is part of finding the largest distance.
- Algorithms are typically described in pseudocode.
- Algorithms are analyzed for speed independent of machine/language.
- Algorithms are usually analyzed along with the problems they solve.
(Analyzing a problem is often harder).
Describing algorithms: pseudocode
What is pseudocode?
- A language-independent description of an algorithm.
- Various "levels" of pseudocode:
- Very-high level pseudocode, e.g., for Algorithm1 above:
1. Scan through all possible pairs of numbers in the array.
2. For each such pair, compute the absolute difference.
3. Record the largest such difference.
- English-like pseudocode:
Input: an array of numbers, A
1. Set the initial maximum to the difference between the first two
in the array.
2. Loop through all possible pairs of numbers:
2.1 For each such pair, see if it's difference is larger
than the current maximum.
2.1.1 If so, record the new maximum and the values
that achieved it.
3. Output the maximum found.
- Detailed pseudocode, as found in many algorithms books:
Algorithm1 (A)
Input: A, an array of numbers.
// Set the initial maximum to the difference between the first two:
1. max = Absolute-Difference (A[0], A[1]);
// Record the actual values:
2. x = A[0], y = A[1];
// Now compare each pair of numbers:
3. for i=0 to length-1:
4. for j=i+1 to length
// For each such pair, see if it's difference is larger
// than the current maximum.
5. diff = Absolute-Difference (A[i], A[j]);
6. if (diff > max)
// If so, record the new maximum and the values
// that achieved it.
7. max = diff;
8. x = A[i]; y = A[j];
9. endif
10. endfor
11. endfor
Output: min, max, diff
Note:
- Such pseudocode usually does not contain variable
declarations or data-types
(They are usually implied or left to the reader)
- The pseudocode "language" is fictitious.
- Boldface is usually used for keywords.
- Not all methods/functions are shown, especially when
the meaning is obvious.
- Pseudocode (all levels) is extremely useful in describing algorithms.
- Notice how easy it is to express the key idea in high-level pseudocode.
- Recommended practice:
- Provide high-level pseudocode at the very minimum.
- Provide separate detailed pseudocode where possible,
usually in manuals or written documentation.
- Include the high-level pseudocode at the beginning
of a program.
- Include the detailed pseudocode as comments in the program.
Analysing algorithms
Algorithms are analysed using the so-called "order notation":
- The order-notation is initially confusing to learn.
- Once mastered, it makes analysis easier and definitely easy to present.
- The key idea: pay attention only to important details.
Consider the following example:
for (int i=0; i < A.length-1; i++){
for (int j=i+1; j < A.length; j++) {
double diff = Math.abs (A[i] - A[j]);
if (diff > max)
max = diff;
}
}
Let's analyse this piece of code:
- The outer loop is executed A.length-1 times.
- For the i-th outer loop iteration, the inner one is executed
A.length-i times.
- In the inner loop, the Math.abs function is called
every time.
- The assignment inside the if is not always executed.
- Assume it takes about s seconds for one iteration of
the inner loop.
- How many seconds overall?
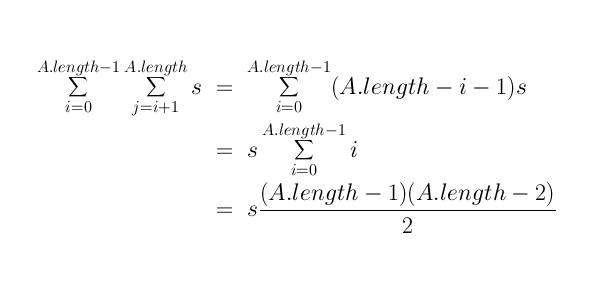
First, it's preferable to use math symbols:
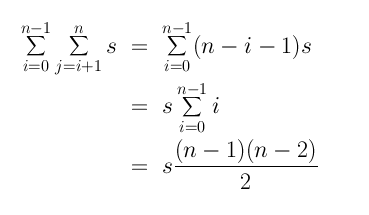
It is possible to simplify further by observing that
(n-1)(n-2)/2 = n2/2 -3n/2 + 1.
Observe: the term that dominates is
n2/2.
Accordingly, for purposes of approximate analysis:
- Ignore the "lower-order" terms.
- Ignore constants.
=> The algorithm requires O(n2) steps.
Background math
A quick math review:
- What is a function?
- A formal definition requires more set-theory definitions.
- But we have an intuitive idea:
e.g., f(x) = x2 implies f(3) = 32 = 9.
- Informally:
- A domain of possible arguments - "what the function takes".
- A range - "what the function produces".
- For any argument, a unique result.
In-Class Exercise 6:
Use a calculator and plot the following functions in the range
(0,100) by "joining the dots" of function values computed
at 0, 10, 20, ..., 100:
- f(x) = x
- f(x) = x2
- f(x) = log2(x)
- f(x) = xlog2(x)
- f(x) = 2x
- f(x) = ex
- Useful exponentiation rules:
- xa xb = xa+b
- xa / xb = xa-b
- (xa)b = xab
- Logarithms:
- What exactly are they?
=> the "inverse of exponentiation"
- Definition: y = loga(x) if ay = x
- Example: What is log2(256)?
2? = 256?
28 = 256
Thus, log2(256) = 8.
- Another way of thinking about it:
- Divide 256 by 2 to get: 256 / 2 = 128.
- Then, 128 / 2 = 64
- ...
- How many times do we need to divide by 2 to get 1?
log2256 times.
- What do logarithms have to do with algorithms? (e.g., searching)
- Consider an algorithm to search a data set of size n.
- Break up the data into two pieces (size n/2 each).
- Figure out (quickly) which piece has the data.
- Continue the search with data set of size n/2.
- Repeat the procedure.
How long does this procedure take?
How many times can you recursively break up the data into two pieces?
Ans: log(n) times.
Thus, the procedure takes about log(n) steps.
- Note: loge(x) is sometimes denoted lne(x)
In-Class Exercise 7:
Use the definition of logarithms and the exponentiation rules to
show that: loga(xy) = loga(x) + loga(y).
- Useful sums:
- 1 + 2 + 3 + ... + n = n(n+1)/2
- 1 + a + a2 + a3 + ... + an
= (an+1 - 1) / (a - 1)
- 1 + a + a2 + a3 + ...
= 1/(a - 1) when 0 < a < 1 (infinite sum)
- 1 + 1/2 + 1/3 + 1/4 + ... + 1/n approx. equals logen
The order notation
Consider the functions:
- f(n) = 9n2 + 1000n
- g(n) = n3
Think of f(n) as the time taken by some algorithm, and
g(n) as some function that will be useful for analysis.
In-Class Exercise 8:
Download and execute TwoFunction.java.
You will also need Function.java
and SimplePlotPanel.java.
- Confirm that the functions f and g are being plotted.
- At what value of n does g(n) rise above f(n)?
Order notation:
- We sense from the above example that f(n) is "less than" g(n).
- But that is not always true.
=> not true for n = 10.
- Possible definition 1:
f(n) = O(g(n)) if
f(n) ≤ g(n) for all large enough n.
- This is often written as:
f(n) = O(g(n)) if there is some N such that
f(n) ≤ g(n) for all n > N
- How to say it aloud: f(n) is "Oh-of" g(n) or
"Big-Oh-of" g(n).
In-Class Exercise 9:
Consider f(n) = 9n2 and
g(n) = n2. Is f(n) = O(g(n))?
- However, the dominant term in f(n)=9n2
is n2
We'd like to say that f(n)=9n2 is "of
the order of" g(n)=n2.
- They are of the same order except for a constant multiplying factor.
- Possible definition 2:
f(n) = O(g(n)) if there exists a constant c
such f(n) ≤ c g(n).
In-Class Exercise 10:
Consider f(n) = 9n2 and
g(n) = n2. What choice of c suffices
to show f(n) = O(g(n)) by the above definition?
- Does this always work?
In-Class Exercise 11:
Consider f(n) = 9n2 + 1000n and
g(n) = n2. Is there a choice of c
such that f(n) = O(g(n)) by the above definition?
- Possible definition 3:
f(n) = O(g(n)) if there exists constants c
and N such that f(n) ≤ c g(n)
for all n > N.
In-Class Exercise 12:
Consider f(n) = 9n2 + 1000n and
g(n) = n2. Suppose c=10.
Is there a value of N such that
f(n) ≤ c g(n) for all n > N?
Plot f and g by modifying the code
in TwoFunction.java.
- Suppose we pick c=100. Then
100 g(n)
= 100n2
= 9n2 + 91n2
Thus,
100g(n) ≥ f(n)
if
9n2 + 91n2 ≥ 9n2 + 1000n.
Which will be true if
91n2 ≥ 1000n.
Which will be true if
n ≥ 11
Thus, c=100, N=11 is sufficient to prove
that f = O(g).
- Thus, the higher we pick c, the lower N needs
to be.
In-Class Exercise 13:
What value of N is sufficient when c=1000?
All of the above reasoning leads to this definition:
- Definition: We say that
f(n) = O(g(n)) if there exists a constant c
such f(n) ≤ c g(n) for all n≥1.
Note:
Related definitions:
- We say that f(n) = Ω(g(n)) if g(n) = O(f(n))
=> Informally, f is at least as large as g, e.g.,
f(n)=4n3 and g(n)=6n2.
- We say that f(n) = Θ(g(n)) if both
f(n) = Ω(g(n)) and f(n) = O(g(n))
=> Informally, f and g are of the same order, e.g.
f(n)=4n3+8n2 and g(n)=n3+n.
In-Class Exercise 16:
Implement and analyze the Selection Sort algorithm:
- SelectionSort works like this: Suppose the array is in
data[i].
First find the smallest element and put that in
data[0].
Then find the smallest element in the range
data[1],...,data[data.length-1]
and put that in
data[1], etc.
- Download SelectionSort.java
and UniformRandom.java.
- Write your code in the file SelectionSort,
to sort a data set of integers.
- Then test by executing SelectionSort.
- If f(n) denotes the number comparisons made by
SelectionSort for a data set of size n, what is the smallest
value of k for which f(n) = O(nk)?
- Count the number of comparisons - does your experimental
evidence match the analysis?
- Do the number of comparisons depend on the input data?
Worst-case and other comparisons
Consider comparing two algorithms A and B on the sorting problem:
- On some data sets A might perform better than B.
On others, B might perform better.
How to compare them?
- The standard approach: a worst-case order analysis:
- Other approaches:
- Best-case (theoretical)
- Average-case (theoretical)
- Average-case (experimental)
- Other kinds of issues:
- Complexity of implementation.
- Practical data sets, problem sizes.
- Relation to application, relative importance of algorithm.
- Exploiting architecture, operating systems.
Typical worst-case analysis:
- Assume the worst possible input for the algorithm.
- Identify key operations that take unit time.
- Count number of operations using order notation.
Theoretical average-case analysis:
- Assume a probability distribution over possible inputs.
- Derive expected running time using distribution.
- Express expected running time using order notation.
- Typically very difficult even for simple problems/algorithms.
- Not often practical, even if feasible.
Experimental average-case analysis:
- Compare algorithms on randomly generated data sets.
- Running a single algorithm sometimes makes little sense.
(Depends on processor, system architecture, OS).
- Create different types of data sets (uniform, non-uniform).
- Test over wide range of problem sizes.
- Accompany with worst-case analysis.
A comprehensive analysis of a problem:
- Prove a lower-bound on the problem.
(e.g., sorting cannot be solved faster than O(n log(n))
- Devise a fast algorithm.
- Analyse worst-case complexity of algorithm.
- Experimentally evaluate algorithm: compare with others and lower-bound.
- See if special cases can be solved faster.
Simple timing of a Java program
Use the System.currentTimeMillis() method:
long startTime = System.currentTimeMillis();
// ... algorithm runs here ...
double timeTaken = System.currentTimeMillis() - startTime;
In-Class Exercise 17:
Compare your selection sort implementation with the sort algorithm
in the Java library. Download
SelectionSortTiming.java
and insert your code from the previous exercise.
Famous algorithms
A brief mention of some "famous" algorithms and data structures:
- The Simplex algorithm:
- Used in linear programming, a class of optimization problems.
- Part of almost every optimization package.
- Needs some math background to understand.
- NOT an efficient algorithm (provably faster algorithms
exist), but "undefeated" until recently (by Karmarkar's algorithm).
- FFT:
- Fast Fourier Transform.
- Simple to implement, needs math background to understand.
- Used as a key building-block in just about every signal-processing software.
- Considered the "most used" algorithm of all time.
- Dijkstra's Shortest-Path algorithm:
- Currently the algorithm used for routing in the Internet.
- Simple to implement, using a binary heap.
- Interesting theoretical improvements exist.
- Since tens of thousands of internet routers run this algorithm every
few seconds, perhaps it should be considered the "most executed" algorithm.
- Quicksort:
- Exemplar of the "divide and conquer" technique.
- Easy to implement, hard to beat.
- Poor worst-case performance, excellent average-case performance.
- Hashing:
- Probably the "most used" data structure.
- Useful for "equality" search, sets.
- Except for pathological cases, extremely fast for insertion and retrieval.
- B-tree:
- Devised for accessing external files.
- Variations are used in almost every commercial database system.
- Simple, yet powerful.
- Block-oriented.
- Binary heap:
- Simple, efficient priority queue.
- Used in various graph algorithms.
- Efficient (and unusual) array implementation.
- Can be (but rarely) used for sorting.
- Splay tree:
- Self-balancing, self-adjusting binary tree.
- Less overhead than AVL-trees.
- Opened a new line of analysis: amortized analysis.
- Useful as both a "dictionary" and "priority-queue".
- Simulated Annealing:
- A simple algorithm, based on an interesting metaphor.
- Used for solving combinatorial problems.
- Not very efficient, but very easy to implement.
- The RSA algorithm:
- Named after Rivest-Shamir-Adleman.
- First public asymmetric public-key cryptographic algorithm.
- Easy to implement (but not as easy to implement efficiently).
- Not free - must pay authors royalty.
- Very popular, has made authors very rich.
- Effectiveness recently (2002) called into question by fast
primality testing.
In-Class Exercise 18:
Do a web search on "top ten algorithms".