Exercise 5

  1. Reading: Chapter 16 (pp. 370-383).

  2. Pen-and-paper exercises:
    1. In each of the graph examples below, your graph should have at least 6 nodes.
      1. Draw an example of a graph such that if you remove any one edge, the resulting graph remains connected.
      2. Draw an example of a graph such that if you remove any edge, the resulting graph is not connected.
      3. Draw an example of a graph such that only one edge in the graph has the property that if you remove it, the resulting graph will not be connected.
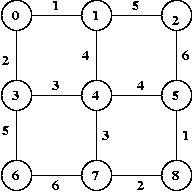
    2. For the graph below, show the steps in executing Kruskal's algorithm and Prim's algorithm. Draw the graph with the MST edges identified at each step.

    Note: Credit will not be given only for answers - show all your work: your reasoning, steps you took to get your answer etc.

  3. In this part, you will use Kruskal's algorithm to estimate the minimum-spanning tree weight of a randomly-created set of points.

    Compute the average weight of the minimum spanning tree for a collection of n random points in the unit square:

    • Consider a set of random points in the plane. For example, suppose these were pegs nailed to a board. Suppose you had to connect these pegs with the least amount amount of string. Note that this is just the minimum spanning tree problem. (You need to think about this for a few minutes). The goal is to compute the weight of the minimum spanning tree for a random set of points. Here, you can assume an "edge" between each pair of points with the distance between as the weight.
    • How do you generate n random points in the unit square? And what is the unit square?
      The unit square is the square with one corner at the origin (0,0) and opposite corner at (1,1). To generate a point randomly, we can use UniformRandom.uniform() to generate a value randomly between 0 and 1 for the X value, and call it once again for the Y value. So, to generate n such X and Y values, you can use this code: 
          for (int i=0; i < n; i++)
      X[i] = UniformRandom.uniform();
    for (int i=0; i < n; i++)
      Y[i] = UniformRandom.uniform();
    • For a given value of n, each set of n random points will have some minimum spanning tree connecting those points and some weight. If you average across different sets of n points, then you will get an average "tree weight" for n points.
    • Report this average for the following values of n: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Use 100 trials for each average.
    • Modify the code given to you in Module 8 for Kruskal's algorithm. Read through this carefully.
    • Name your class Kruskal.java.
    • Your class will need to implement the SpanningTreeAlgorithm interface. In particular, you will need to provide implementations for these methods: initialize(), minimumSpanningTree(double[][] adjMatrix) and getTreeWeight().
    • The classes and interfaces involved in this exercise are:
      The Algorithm interface
      The SpanningTreeAlgorithm interface
    • Also, Kruskal's algorithm will need an implementation of Union-Find. For this purpose, you should create a class called UnionFindInt. You can intuit what this class needs to have from its use in the Module 8 examples.
    • Use the test environment to test your minimum spanning tree algorithm. However, it does not compute the average tree weight. Simply submit your hardcopy and evidence that your code worked for the average-weight problem.
    • Use this properties file for testing your adjacency matrix implementation.

Submission: