Module 9: Recursion, Part II

Supplemental material

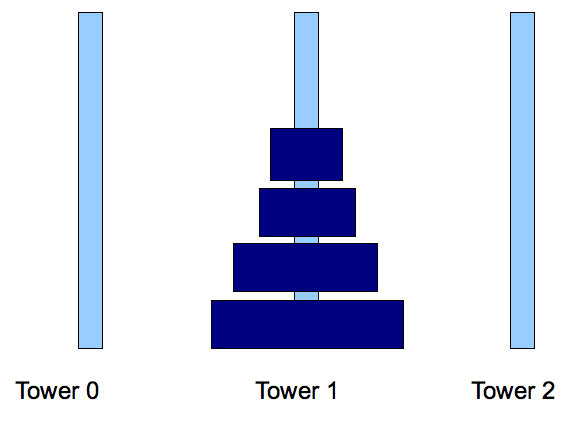
The Tower of Hanoi

In the Tower of Hanoi puzzle:

There are three stacks (towers), numbered 0, 1, 2.

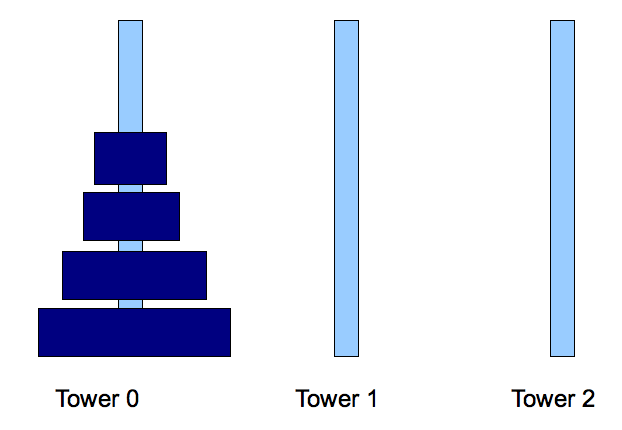
There are N disks numbered 0, ..., N-1.
⇒ 0 is the smallest.

Initially, the disks are placed in tower 0, in the order largest to smallest.
⇒ Smallest on top.

Goal: to move the disks to tower 1 using only legal moves.

What's a legal move?

You can move only a disk at the top of a tower.
You can move only one disk at a time.
You cannot place a disk on top of a smaller one.

In-Class Exercise 1: Work out the moves for the ToH problem with three disks. You can either cut out pieces of paper or find an interactive applet on the web. Write down the moves on paper as in "Step 1: Move disk 0 from tower 0 to tower 1 ..."

We will solve the problem using (of course) recursion:

There are three key steps in the recursion:
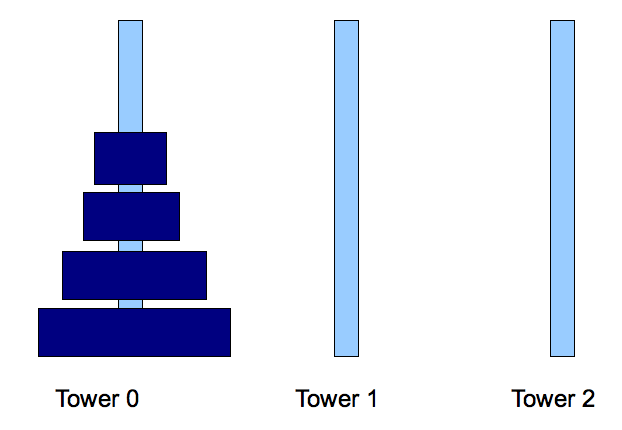
- Step 1: move disks 0, ..., N-2 from tower 0 to tower 2
  ⇒ Sub problem of smaller size.
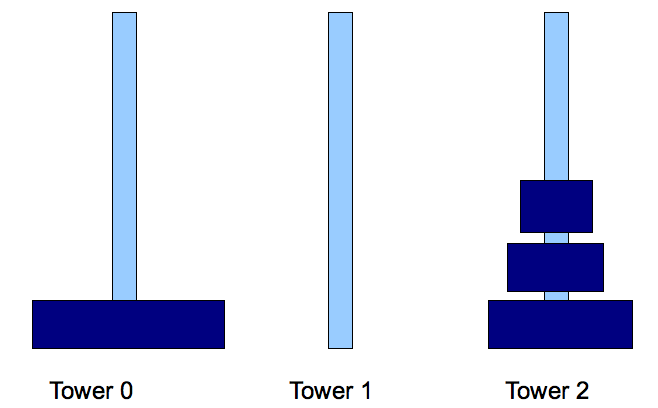
- Step 2: move disk N-1 from tower 0 to tower 1.
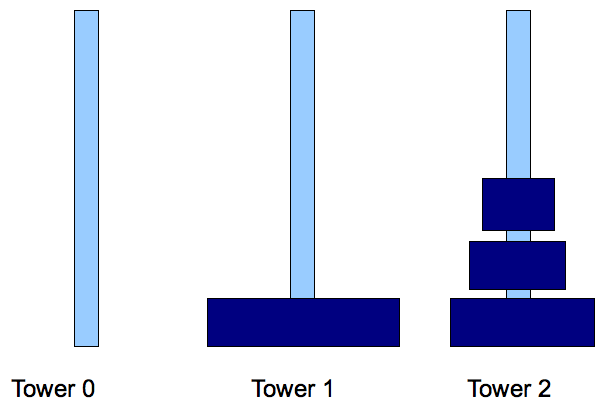
- Step 3: move disks 0, ..., N-2 from tower 2 to tower 1.
  ⇒ Sub problem of smaller size.

In pseudocode (without base case):

     Algorithm towerOfHanoi (n, i, j)
     Input: Disks numbered 0, ..., n are to be moved from tower i to tower j

     1.    // ... base case ...

           // First find the third tower, other than i and j:
     2.    k = otherTower (i, j)

           // Step 1: move disks 0,..,n-1 from i to k
     3.    towerOfHanoi (n-1, i, k)
           // Step 2: move disk# n from i to j
     4.    move (n, i, j)
           // Step 3: move disks 0,...,n-1 from k to j
     5.    towerOfHanoi (n-1, k, j)

The base case: move a single disk

Here's the program:

public class TowerOfHanoi {

    public static void main (String[] argv)
    {
        // A 3-disk puzzle:
        System.out.println ("3-Disk solution: ");
	solveHanoi (2, 0, 1);

        // A 4-disk puzzle:
        System.out.println ("4-Disk solution: ");
	solveHanoi (3, 0, 1);
    }


    static void solveHanoi (int n, int i, int j)
    {
	// Bottom-out.
	if (n == 0) {
            // The smallest disk.
	    move (0, i, j);
	    return;
	}

	int k = other (i, j);
	solveHanoi (n-1, i, k);    // Step 1.
	move (n, i, j);            // Step 2.
	solveHanoi (n-1, k, j);    // Step 3.
    }


    static void move (int n, int i, int j)
    {
        // For now, we'll merely print out the move.
        System.out.println ("⇒ Move disk# " + n + " from tower " + i + " to tower " + j);
    }


    static int other (int i, int j)
    {
        // Given two towers, return the third.
        if ( (i == 0) && (j == 1) ) {
            return 2;
        }
        else if ( (i == 1) && (j == 0) ) {
            return 2;
        }
        else if ( (i == 1) && (j == 2) ) {
            return 0;
        }
        else if ( (i == 2) && (j == 1) ) {
            return 0;
        }
        else if ( (i == 0) && (j == 2) ) {
            return 1;
        }
        else if ( (i == 2) && (j == 0) ) {
            return 1;
        }

        // We shouldn't reach here.
        return -1;
    }

}

Note:

The above program merely prints out the moves needed
⇒ We don't actually maintain the state of each tower.

In-Class Exercise 2: Compile and execute the above program to verify that your "moves" from Exercise 1 were correct.

In-Class Exercise 3: The other() method now has above 10-12 lines of code. Can you rewrite it to have only one line, a very short line, of code? Hint: think of a mathematical property you could exploit.

Next, suppose we want to maintain the state of each tower:

The ideal data structure is a stack.
We'll use one stack for each tower.

Here's the program:


import java.util.*;

public class TowerOfHanoi2 {

    // towers[0], towers[1] and towers[2] are the three stacks.
    static Stack<Integer>[] towers;


    public static void main (String[] argv)
    {
        // A 3-disk puzzle:
        System.out.println ("3-Disk solution: ");
	solveHanoi (2, 0, 1);

        // A 4-disk puzzle:
        System.out.println ("4-Disk solution: ");
	solveHanoi (3, 0, 1);
    }


    static void solveHanoi (int n, int i, int j)
    {
        // Create the three stacks.
	towers = new Stack [3];
	for (int k=0; k<3; k++) {
	    towers[k] = new Stack<Integer>();
	}

        // Put disks 0,...,n on stack 0.
	for (int k=n; k>=0; k--) {
	    towers[0].add (k);
	}

        // Print the initial stack.
	printTowers ();

        // Now solve recursively. Note: this is the method below.
	solveHanoiRecursive (n, i, j);
    }
    

    static void solveHanoiRecursive (int n, int i, int j)
    {
	// Bottom-out.
	if (n == 0) {
	    move (0, i, j);
	    return;
	}
	int k = other (i, j);
	solveHanoiRecursive (n-1, i, k);   // Step 1.
	move (n, i, j);                    // Step 2.
	solveHanoiRecursive (n-1, k, j);   // Step 3.
    }


    static void move (int n, int i, int j)
    {
        // Pull out the top disk on stack i.
	int topVal = towers[i].pop();
        // Put it on stack j.
	towers[j].push (topVal);
        // Print status.
        System.out.println ("Towers after moving " + n + " from tower " + i + " to tower " + j);
	printTowers ();
    }


    static int other (int i, int j)
    {
        // ... 
    }


    static void printTowers ()
    {
	for (int i=0; i<towers.length; i++) {
	    System.out.print ("Tower " + i + ": ");
	    if ( ! towers[i].isEmpty() ) {
		for (Integer I: towers[i]) {
		    System.out.print (" " + I);
		}
	    }
	    System.out.println ();
	}
    }

}

Note:

Since we needed to create the stacks ahead of time, we moved the recursive part of the code into a new recursive method solveHanoiRecursive().

To remove a disk from the top of a tower, we pop() from that tower (stack):

        // Pull out the top disk on stack i.
	int topVal = towers[i].pop();

To place a disk on top of a tower, we push() it:

        // Put it on stack j.
	towers[j].push (topVal);

Notice how printTowers() uses the "collection" version of the for-loop:

	    if ( ! towers[i].isEmpty() ) {
                // New type of for-loop:
		for (Integer I: towers[i]) {
		    System.out.print (" " + I);
		}
	    }

A strange compilation message:
- In compiling the above program (with a Java 1.5 compiler), we get a warning (not an error):
```
Note: TowerOfHanoi2.java uses unchecked or unsafe operations.
Note: Recompile with -Xlint:unchecked for details.
      
```
- This allows you to continue with execution.
- You can, as it suggests, re-compile with the -Xlint:unchecked option:
```
      javac -Xlint:unchecked TowerOfHanoi2.java
      
```
- What you see as a result:
```
TowerOfHanoi2.java:25: warning: [unchecked] unchecked conversion
found   : java.util.Stack[]
required: java.util.Stack[]
        towers = new Stack [3];
                 ^
      
```
- The compiler did not like the statement:
```
        towers = new Stack [3];
       
```
- So, should this instead have been
```
        towers = new Stack<Integer> [3];
       
```
  as one might intuitively expect?
- Unfortunately, that results in a compilation error.
- The reason is quite esoteric and has to do with the gory details of generic types are handled in Java.
- Essentially, it boils down to this: a declaration like
```
        towers = new Stack<Integer> [3];
       
```
  is unsafe because one can assign non-Integer stacks to towers, which is why the compiler doesn't allow it.
- Thus, we are left with using the slightly less unsafe
```
        towers = new Stack [3];
       
```
  which the compiler allows but warns against.
- Generic types in Java constitute a large and somewhat advanced topic, too complicated for this course.

In-Class Exercise 4: Modify TowerOfHanoi2.java to count the total number of moves. How many moves are needed for a puzzle with N disks? Is this a polynomial or exponential algorithm?

An application: disk backup schedules

Suppose we have four disks (A, B, C and D) on which we wish to perform backups each day.
⇒ This is a different meaning of disk (hard drive, removable media)
Each day we need to choose a disk on which to backup
⇒ The backup schedule.

One option is to go round-robin

       Day 0 - use disk A
       Day 1 - use disk B
       Day 2 - use disk C
       Day 3 - use disk D
       Day 4 - use disk A
       Day 5 - use disk B
       ...
       (and so on)

With this system, we can only go back at most four days.
We are not able to retrieve the state of the system from, say, 6 days ago.

Another approach: stagger the disks:

       Day 0 - use disk A
       Day 1 - use disk B
       Day 2 - use disk A
       Day 3 - use disk C
       Day 4 - use disk A
       Day 5 - use disk B
       Day 6 - use disk A
       Day 7 - use disk D
       Day 8 - use disk A
       ...
       (and so on)

With this approach, we'd have a distribution like

         Disk A - 1 or 2 days before
         Disk B - at most 4 days before
         Disk C - at most 8 days before
         Disk D - at most 16 days before

This distribution allows a deeper reach into the past.

The sequence above is exactly the Tower-of-Hanoi move sequence for disks numbered A, B, C and D.

In-Class Exercise 5: Modify TowerOfHanoi3.java to print out the disk-backup schedule for disks A, ..., E (five disks).

Recursion: a review

First, let's review a simple example from Module 4:

Recall the recursive computation of power:

    // Compute a^b

    static int power (int a, int b)
    {
        // Bottom-out:
        if (b == 0) {
            return 1;
        }

        // Recursion:
        return (a * power (a, b-1));
    }

What's important:

We must test for the bottom out case before recursing.
The bottom-out case tests the value (or values) of the parameter (or parameters) that changes in the recursion.
⇒ These are the parameters that control the recursion.
The recursive calls must change (usually decrease) the parameters that control the recursion.
⇒ Above, there is only one recursive call, but Tower of Hanoi has two.

How recursion works:

Each method call creates an activation record on the system stack.
The activation record consists of space allocated for the particular parameters and local variables for that method call.
Thus, a recursive call results in a new activation record for each such recursive call.
⇒ This is why each execution of the method retains its own parameters and local variables.
The activation record also knows that when execution of a method call completes, execution returns to the calling method just after the called-method was called.
For recursion it's no different except that it's the same code involved in all method calls.

The best way to understand recursion initially is to draw the stack picture and work through an example.

In-Class Exercise 6: Draw the stack picture at each step (call) for the first TowerOfHanoi example, using three disks. How many stack snapshots are in the drawing?

Let's now review another example from Module 4:

This is the permutation seating example where we print the arrangement:

    // The parameters to this method are:
    //    numSpaces - total number of remaining seats available
    //    numRemaining - total number of people left to seat
    //    seats - an array where seats[i]==0 if seat is available
    //    person - which person we need to seat

    static void printPermutations (int numSpaces, int numRemaining, int[] seats, int person)
    {
        // Bottom-out case. 
	if (numRemaining == 0) {
	    // Print.
	    System.out.println ( Arrays.toString(seats) );
	    return;
	}

	// Otherwise, non-base case: look for an empty spot for "person"
	for (int i=0; i < seats.length; i++) {
	    if (seats[i] == 0) {

		// Empty spot.
		seats[i] = person;

                // Recursively assign remaining, starting with person+1
		printPermutations (numSpaces-1, numRemaining-1, seats, person+1);

                // Important: we need to un-do the seating for other trials.
		seats[i] = 0;
	    }
	} //end-for
    }

What's similar about this recursive method:
- The parameter that controls recursion is: numSpaces
  ⇒ This is what we check in the bottom-out case.
- Other parameters pass along information: person and seats.

What's different (from the power() example):

When we fill in the seats array, we un-do this assignment after the recursive call:

                // Make some change to a parameter:
		seats[i] = person;

                // Recurse:
		printPermutations (numSpaces-1, numRemaining-1, seats, person+1);

                // Un-do the change (restore the original) for future recursions:
		seats[i] = 0;

Two types of recursion:

Recursion where you don't un-do changes.
⇒ Sometimes this is called tail recursion.
Recursion where you need to un-do changes so that you can properly explore all possibilities
⇒ Sometimes this is called recursion with backtracking.
Many examples of tail-recursion can easily be written non-recursively (using iteration)
⇒ For many of these examples (power, factorial, fibonacci), it's better to use iteration.
However, when there's backtracking, it can be very difficult to avoid recursion.

In-Class Exercise 7: Which kind of recursion is TowerOfHanoi.java?

Maze construction and traversal: a (long) example of recursion with backtracking

We will now examine a maze application in detail to illustrate recursion with backtracking:

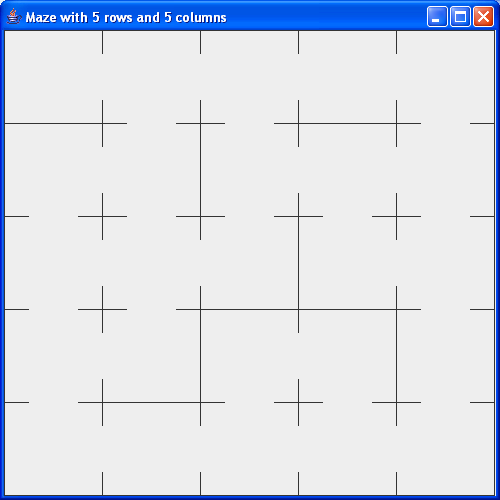
First, we will use recursion to create a maze like this:

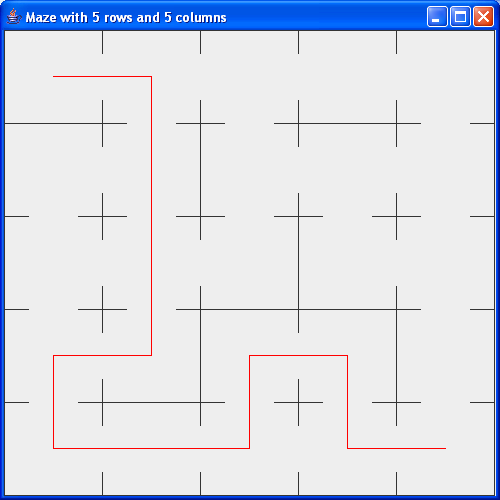
Then, we will use recursion to solve such a maze (by finding a path from a given start cell (e.g., the topleft) to a given end cell (e.g., the bottom right):

We will put a whole bunch of useful code in a class called Maze and instead focus on using that class through its methods.

We'll use this cell-numbering convention:

Rows start numbering at 0, and increase downwards.
Columns start at 0 and increase rightwards.

Thus, the topleft cell is (0,0). The one to its right is (0,1) and the one directly below is (1,0).

To start with, let's examine the methods in the class Maze:

The constructor: we create an instance by specifying the number of rows and columns:
```
     Maze maze = new Maze (5, 5);
     
```
Our examples will use square mazes.

display(): call this method to display the maze:

     Maze maze = new Maze (5, 5);

     // Bring up the GUI:
     maze.display ();

breakWall():

Initially, the maze consists of complete cells. To actually create a walkable maze, we will "break walls" between neighboring cells.

For example, we can break the wall between cells (3,4) and (2,4) as follows:

        Maze maze = new Maze (5, 5);

        // Note the use of the Coord class:
        Coord c1 = new Coord (3,4);
        Coord c2 = new Coord (2,4);
        maze.breakWall (c1, c2);

        maze.display ();

Or, alternatively, with shorter code:

        Maze maze = new Maze (5, 5);

        // Create an instance directly in the method argument list:
        maze.breakWall (new Coord(3,4),  new Coord (2,4));

        maze.display ();

The Coord class looks like this:

public class Coord {

    public int row=-1, col=-1;

    public Coord (int r, int c)
    {
        row = r;
        col = c;
    }
    
    public String toString ()
    {
        return "[" + row + "," + col + "]";
    }
    
}

Thus, to access the stored coordinates:

      Coord c = new Coord (3,4);
      System.out.println ("Row=" + c.row + " Col=" + c.col);
      // Or, to print both using toString():
      System.out.println (c);

A number of methods (in the class Maze) allow us to mark and un-mark cells as visited:
- markVisited (Coord c): mark cell c as visited.
- markUnVisited (Coord c): mark cell c as not visited.
- markAllUnvisited(): mark all cells as unvisited.
- isVisited (Coord c): see whether cell c has been visited.
A number of methods related to fetching a list (array) of a cell's neighbors:
- Coord[] getUnvisitedClosedNeighbors (Coord c): get cell c's neighbors that are closed off from c (there's a wall between) and haven't been visited yet.
- Coord[] getClosedNeighbors (Coord c): get neighbors of c that share a wall (unbroken) with c whether visited or not.
- Coord[] getUnvisitedOpenNeighbors (Coord c): get those neighbors of c for which we can walk through to the neighbor (no wall) and which haven't been visited.
Each of these methods return an array of Coord instances.

A few additional useful methods:

copy(): make a full copy of the maze, as in:

       Maze m = new Maze (5,5);
       // ... do stuff: break walls etc ...
       Maze m2 = m.copy();
       // Now m2 is a copy of m. Making changes to m won't affect m2.

setSolutionPath (LinkedList<Coord> solutionPath): we will call this method once we have constructed a solution.

In-Class Exercise 8: Download Maze.java (which you don't have to read) and modify MazeByHand.java to draw a maze path from (3,4) to (1,1). Do this by breaking walls. You can type in each wall-break separately using calls to breakWall(). Then, when that's working, create a solution path and display it.

We'll now write our first attempt:

We will try to generate a maze path of a given path length.

The key idea:

     Algorithm: recursiveGenerate (Coord c)
     1.   if path-length has been reached
     2.     return
          // Otherwise ...
     3.   c' = Pick a random neighbor of cell c
     4.   recursiveGenerate (c')

Here's the program:

public class MazeMaker {

    // These variables will be used across methods:
    static int desiredPathLength;    
    static Maze maze;


    public static void main (String[] argv)
    {
        generateMaze (5, 5);
    }


    public static void generateMaze (int numRows, int numCols)
    {
        maze = new Maze (numRows, numCols);

        // We want to generate a path of this length:
	desiredPathLength = numRows * numCols;

	// Initially, we'll start with the top left cell and mark that as visited.
        Coord start = new Coord (0, 0);
	maze.markVisited (start);

        // Generate the maze path recursively.
	boolean found = recursiveGenerate (start, 1);

        if (! found) {
            System.out.println ("Could not create the whole maze");
        }
        maze.display();
    }


    static boolean recursiveGenerate (Coord c, int pathLength)
    {
        // Bottom out condition 1:
	if (pathLength == desiredPathLength) {
	    // Done. We've create a maze path of the desired length.
	    return true;
	}

        // Bottom out condition 2: see if there's a neighbor to visit.
	Coord[] validNeighbors = maze.getUnvisitedClosedNeighbors (c);
	if ((validNeighbors == null) || (validNeighbors.length == 0)) {
            // There's no neighbor whose wall we can break. So quit trying.
	    return false;
	}

        // Otherwise, pick a random neighbor and proceed.
        int i = UniformRandom.uniform (0, validNeighbors.length-1);

        // Break the wall and mark the neighbor as visited.
        maze.breakWall (c, validNeighbors[i]);
        maze.markVisited (validNeighbors[i]);
            
        // Recurse.
        return recursiveGenerate (validNeighbors[i], pathLength+1);
    }

}

In-Class Exercise 9: Download Maze.java and and MazeMaker.java. You will also need UniformRandom.java. Then compile and execute. Why doesn't it produce a path of the desired length?

Next attempt:

Simple tail recursion can get stuck.
⇒ We need a way to "un-do" paths and try different neighbors.
We will pick a neighbor to explore recursively
⇒ If that doesn't work out, we'll try another.

Here's the program:

public class MazeMaker2 {

    static int desiredPathLength;
    static Maze maze;


    public static void main (String[] argv)
    {
        generateMaze (5, 5);
    }


    public static void generateMaze (int numRows, int numCols)
    {
        maze = new Maze (numRows, numCols);

	desiredPathLength = numRows * numCols;

	// Initially, we'll start with the top left cell.
        Coord start = new Coord (0, 0);
	maze.markVisited (start);

        // Generate the maze path recursively.
	boolean found = recursiveGenerate (start, 1);

        if (! found) {
            System.out.println ("Could not create the whole maze");
        }
        maze.display();
    }


    static boolean recursiveGenerate (Coord c, int pathLength)
    {
        // Bottom out condition 1:
	if (pathLength == desiredPathLength) {
	    return true;
	}

        // Bottom out condition 1: see if we're stuck.
	Coord[] validNeighbors = maze.getUnvisitedClosedNeighbors (c);
	if ((validNeighbors == null) || (validNeighbors.length == 0)) {
	    return false;
	}


	// Otherwise, we have some neighbors to explore.
	// Permute the directions randomly.
	permute (validNeighbors);

	for (int i=0; i < validNeighbors.length; i++) {

            // Try neighbor i.
            maze.breakWall (c, validNeighbors[i]);
            maze.markVisited (validNeighbors[i]);
            
	    boolean ok = recursiveGenerate (validNeighbors[i], pathLength+1);
	    if (ok) {
                // If neighbor i worked out, great.
		return true;
	    }

	    // Otherwise, undo assignment to i.
	    maze.fixWall (c, validNeighbors[i]);
	    maze.markUnvisited (validNeighbors[i]);

	} // end-for

	// Couldn't make it work.
	return false;
    }


    static void permute (Coord[] coords)
    {
	for (int i=0; i < coords.length; i++) {
	    // Find a random element to place into i-th place.
	    int k = (int) UniformRandom.uniform (i, coords.length-1);
	    Coord temp = coords[i];
	    coords[i] = coords[k];
	    coords[k] = temp;
	}
    }

}

Note:

The key idea is to try as many neighbors as needed:

     Algorithm: recursiveGenerate (Coord c)
     1.   if path-length has been reached
     2.     return true
     3.   endif
          // Otherwise ...
     4.   for each neighbor c' of c
     5.     found = recursiveGenerate (c')
     6.     if found
     7.       return true
     8.     endif
     9.   endfor
          // We reach here only if every neighbor did not work out.
     10.  return false

Note how we un-do a broken wall:

	for (int i=0; i < validNeighbors.length; i++) {
            // Try neighbor i.
            maze.breakWall (c, validNeighbors[i]);
            maze.markVisited (validNeighbors[i]);
            
            // ... recursion here ...

	    // To un-do: repair the wall and mark as UNvisited.
	    maze.fixWall (c, validNeighbors[i]);
	    maze.markUnvisited (validNeighbors[i]);
	} // end-for

In-Class Exercise 10: Download MazeMaker2.java, compile and execute. Does it produce a complete path covering all cells? What do you notice about the execution time? Try making this a 6x6 maze with desired path-length 36.

A maze with choices:

The above maze path has no choices
⇒ There's only one way from the topleft to the end of the path.
We will build upon this to create a maze with choices
⇒ After generating the long path, we'll break some random walls.

Here's the program:


public class MazeMaker3 {

    // ... variables ...

    public static void main (String[] argv)
    {
        generateMaze (5, 5);
    }


    public static void generateMaze (int numRows, int numCols)
    {
        // ... create and generate single-path maze ...

        // Break a few more walls, randomly.
        breakRandomWalls (maze, 10);

        maze.display();
    }


    static boolean recursiveGenerate (Coord c, int pathLength)
    {
        // ... same as before ...
    }

 
    static void breakRandomWalls (Maze maze, int numWalls)
    {
	for (int k=0; k < numWalls; k++) {
            // Create random coordinates, i.e., identify a random cell.
	    int x = UniformRandom.uniform (0, maze.numRows-1);
	    int y = UniformRandom.uniform (0, maze.numCols-1);
	    Coord c = new Coord (x,y);

            // Get its neighbors that are separated by a wall.
	    Coord[] validNeighbors = maze.getClosedNeighbors (c);
	    if (validNeighbors != null) {
                // Pick one and break the wall.
                int m = UniformRandom.uniform (0, validNeighbors.length-1);
		maze.breakWall (c, validNeighbors[m]);
	    }
	}
    }

}

In-Class Exercise 11: Download MazeMaker3.java, compile and execute. Solve by hand the maze generated: start at the top-left corner and find a path to the bottom-right corner.

Let's turn our attention to solving the maze:

We'll first try a simple idea:

     Algorithm: recursivelyFindPath (Coord c)
     1.   if c is the end
     2.     return true
     3.   endif
     4.   // Otherwise search further ...
     5.   c' = pick a random "open" neighbor 
     6.   if c' is null
            // Stuck: couldn't find a path.
     7.     return false
     8.   endif
     9.   return recursivelyFindPath (c')

Here's the program:

import java.util.*;

public class MazeMaker4 {

    static int desiredPathLength;
    static Maze maze;


    public static void main (String[] argv)
    {
        Maze maze = generateMaze (5, 5);
	if (maze != null) {
            // We will seek a path from the top-left to the bottom-right corner.
	    Coord start = new Coord (0,0);
	    Coord end = new Coord (4,4);
	    solveMaze (maze, start, end);
	    maze.display ();
	}
	else {
	    System.out.println ("Maze creation did not work");
	}
    }


    // A path is a list of cells, i.e., a list of Coord instances.
    static LinkedList<Coord> solutionPath;


    static void solveMaze (Maze maze, Coord start, Coord end)
    {
        // We'll mark visited cells as we go along our path. Initially:
	maze.markAllUnvisited ();

        // Mark the start cell as visited.
	maze.markVisited (start);

        // Create the list.
	solutionPath = new LinkedList<Coord> ();

        // Recursively find the path and fill in coord's into the list.
	recursivelyFindPath (maze, start, end);

        // Pass the path into the GUI.
	maze.setSolutionPath (solutionPath);
    }


    static boolean recursivelyFindPath (Maze maze, Coord c, Coord end)
    {
        // First add the current cell into the path.
	solutionPath.add (c);

        // If we've reached the end, we're done.
	if ( (c.row == end.row) && (c.col == end.col) ) {
	    return true;
	}

        // Otherwise, let's find a neighbor to explore.
	Coord[] validNeighbors = maze.getUnvisitedOpenNeighbors (c);

	if (validNeighbors == null) {
            // If there aren't any, we're done, but couldn't find a path.
	    return false;
	}

	// Take the first one and explore from there.
	maze.markVisited (validNeighbors[0]);

	return recursivelyFindPath (maze, validNeighbors[0], end);
    }


    // ...  Maze generation code ... same as before ...

}

In-Class Exercise 12: Download MazeMaker4.java, compile and execute. Does it find a solution? Why not?

A solution that works:

When exploring a neighbor, we need a way to un-do (backtrack) if it doesn't lead to a solution.

The idea is to try all possible neighbors, as many as needed:

     Algorithm: recursivelyFindPath (Coord c)
     1.   if c is the end
     2.     return true
     3.   endif
     4.   // Otherwise search further ...
     5.   for each "open" neighbor c'
     6.      found = recursivelyFindPath (c')
     7.      if found
     8.        add c' to path
     9.        return true
     10.     endif
     10.  endfor
     11.  return false

Here's the program:

import java.util.*;

public class MazeMaker5 {

    // ... variables ... same as before (for generation) ...


    public static void main (String[] argv)
    {
        // ... same ...
    }


    // A path is a list of cells, i.e., a list of Coord instances.
    static LinkedList<Coord> solutionPath;


    static void solveMaze (Maze maze, Coord start, Coord end)
    {
        // We'll mark visited cells as we go along our path. Initially:
	maze.markAllUnvisited ();

        // Mark the start cell as visited.
	maze.markVisited (start);

        // Create the list.
	solutionPath = new LinkedList<Coord> ();

        // Recursively find the path and fill in coord's into the list.
	recursivelyFindPath (maze, start, end);

        // The start node gets added last. Why?
        solutionPath.addFirst (start);

        // Pass the path into the GUI.
	maze.setSolutionPath (solutionPath);
    }


    static boolean recursivelyFindPath (Maze maze, Coord c, Coord end)
    {
        // If we've reached the end, we're done.
	if ( (c.row == end.row) && (c.col == end.col) ) {
	    return true;
	}

        // Otherwise, let's find a neighbor to explore.
	Coord[] validNeighbors = maze.getUnvisitedOpenNeighbors (c);
	if (validNeighbors == null) {
            // If we couldn't find any neighbors to explore, we're stuck.
	    return false;
	}

        // Try each neighbor, as many as needed.

        for (int i=0; i < validNeighbors.length; i++) {

            // Try neighbor i.
	    maze.markVisited (validNeighbors[i]);
	    boolean found = recursivelyFindPath (maze, validNeighbors[i], end);

	    if (found) {
                // Notice that we add this to the front of the list, and only
                // after the solution has been found up to here.
		solutionPath.addFirst (validNeighbors[i]);
		return true;
	    }
            
            // If neighbor i didn't work out, un-do the visit and continue.
	    maze.markUnvisited (validNeighbors[i]);
	}

        // If we reached here, then none of the neighbors worked out.
	return false;
    }

}

In-Class Exercise 13: Download MazeMaker5.java, compile and execute. Does it find a solution? Then add code to answer these questions:

How many dead-end's are reached in trying to find a path? Add code to count such dead-end's.

What does a trace look like? Add copious println's to see how the recursion works. Use the indented printing we studied in Module 4.

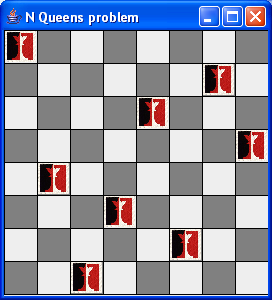
The N-Queens problem

In this problem:

We are given an N x N chessboard and M queens (where M <= N).

The goal is to place the queens on the board so that no queen "attacks" another.

For example (N=8):

Recall that a queen can attack any square in its row, column or diagonal, e.g.

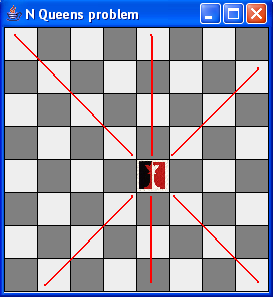
We will of course solve this recursively:

This is another example of recursion with backtracking.
Key ideas:
- We'll proceed columm-by-column (left to right).
- When solving for the current column, try to place a queen on each possible row, and solve the sub-problem (starting with the next column) recursively.

Pseudocode:

    Algorithm: solve (n, c)
    Input: n = the number of queens to assign, c = the column to start with
 
            // ... Bottom-out conditions ... (we'll do this later) 

       1.   for each row r
       2.     if [r,c] is a non-attacked square
       3.        place queen n on cell [r,c]
       4.        found = solve (n-1, c+1)               // Assign remaining n-1 recursively
       5.        if (found)
       6.          return true
       7.        endif
       8.     endif
       9.   endfor
            // We reach here if none of the rows in column c worked out.
       10.  return false

Thus, we try every row for a queen and try to solve the sub-problem with fewer queens.
⇒ If if that gets solved, we can place the queen there and recurse back up
The bottom-out conditions:
- Check if there are no more queens to assign
  ⇒ Problem gets solved.
- Check if there are no more columns to try
  ⇒ No solution exists.
We will build a class called ChessBoard with methods that hide most of the messy board-manipulation details:
- addQueen (row,col): add a queen in square [row,col].
- removeQueen (row,col): remove the queen in square [row,col].
- boolean isForbidden (row,col): see if [row,col] is an attacked square.
- display(): to bring up a GUI with the board displayed.

Here's the program:

import java.awt.*;
import java.util.*;

public class NQueens {

    static ChessBoard board;


    public static void main (String[] argv)
    {
        solveQueens (8, 8);
    }


    static void solveQueens (int numQueens, int size)
    {
        board = new ChessBoard (size);

        boolean solutionExists = solve (numQueens, 0);

        if (! solutionExists) {
            System.out.println ("No solution for " + numQueens + " on a " + size + " x " + size + " board");
            return;
        }

        System.out.println ("Solution found for " + numQueens + " on a " + size + " x " + size + " board");

        System.out.println (board);
        board.display();
    }
    

    static boolean solve (int numQueens, int whichCol)
    {
        // Bottom-out condition 1:
        if (numQueens == 0) {
            // None to assign - done.
            return true;
        }
        

        // Bottom-out condition 2:
        if (whichCol >= board.size()) {
            // No columns left to try - done.
            return false;
        }
        
        // Try every un-forbidden spot in each row.
        for (int row=0; row < board.size(); row++) {
            if ( ! board.isForbidden(row,whichCol) ) {

                // Try this location.
                board.addQueen (row, whichCol);
                
                boolean solutionExists = solve (numQueens-1, whichCol+1);

                if (solutionExists) {
                    return true;
                }

                // Else, un-do
                board.removeQueen (row, whichCol);
            }

        }
        
        // Couldn't find a solution.
        return false;
    }

}

In-Class Exercise 14: Can 3 queens be placed on a 3x3 board? Can 3 queens be placed on a 4x4 board? Download and modify NQueens.java and ChessBoard.java to find out. You will also need ImageTool.java and queen.jpg.