Module 4: Supplemental Material
Binary search
First, let's consider a simple search in an array:
public class SimpleSearch {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = {51, 24, 63, 73, 42, 85, 71, 41, 87, 32};
// Create a test value to search for.
int searchTerm = 32;
boolean found = search (testData, searchTerm);
// Print result.
System.out.println ("found = " + true);
}
static boolean search (int[] A, int value)
{
for (int i=0; i < A.length; i++) {
if (A[i] == value) {
return true;
}
}
return false;
}
}
Note:
- We perform a comparison at each position in the array, until
found.
- We could get lucky and find the search-term near the
beginning.
- We could, equally, be unlucky and have to search the whole array.
⇒
n comparisons in the worst-case for an array of size n.
Now suppose the array were sorted:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- We "know" that 32 is towards the front
⇒
Can we make use of that?
- For example, if we were to search for 51, should we
start the search near the middle?
⇒
Could we somehow make use of the data itself to guide the search?
The key ideas in binary search:
- Consider this sorted array:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- Suppose we are searching for 32.
- First, start by examining three elements:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
^ ^ ^
- By looking at these three, we can tell which half
of the array the search term cannot lie in.
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87] // Cannot lie in the upper half
⇒
Clearly, since 32 < 51, it (32) can't lie in
the region past 51.
- Thus, with a simple comparison, we eliminate half the array.
- The logical next step, is now to apply the same reasoning to
the lower half:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
^ ^ ^
- Here, we've divided the range from 24 to
51 into two pieces by focusing on the middle
element 41.
- By a simple comparison with 41, we can eliminate
the range 41, ..., 51.
- Again, we've eliminated half the array we started with.
- This leaves us with the range
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- Repeating the idea, we examine 32
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
⇒
In this case, we found 32.
- If we were searching for 31, we could declare "not found".
- Note: Binary search works only for sorted arrays.
Now let's examine the program:
public class BinarySearch {
public static void main (String[] argv)
{
// Sorted array:
int[] testData = {24, 32, 41, 42, 51, 63, 71, 73, 85, 87};
// Create a test value to search for.
int searchTerm = 32;
// Note: initially, the "range" is 0,...,testData.length-1
boolean found = binarySearch (testData, searchTerm, 0, testData.length-1);
// Print result.
System.out.println ("found = " + found);
// Another search.
searchTerm = 55;
found = binarySearch (testData, searchTerm, 0, testData.length-1);
System.out.println ("found = " + found);
}
static boolean binarySearch (int[] A, int value, int start, int end)
{
// Bottom-out cases:
if (start == end) {
// There's only one value to check: A[start]=value?
if (A[start] == value) {
return true;
}
else {
return false;
}
}
// If there are only two values in the range:
if (end == start+1) {
if (A[start] == value) {
return true;
}
else if (A[end] == value) {
return true;
}
else {
return false;
}
}
// Otherwise recurse. We know that A[start] <= value <= A[end].
// Find the middle:
int mid = (start + end) / 2;
if (value <= A[mid]) {
// Search the left half: A[start],...,A[mid]
return binarySearch (A, value, start, mid);
}
else {
// Search the right half: A[mid+1],...,A[end]
return binarySearch (A, value, mid+1, end);
}
}
}
Note:
- Initially, when binarySearch() is first called, the
range is 0 to the end of the array.
- Consider the recursive call:
// Search the left half: A[start],...,A[mid]
return binarySearch (A, value, start, mid);
Here, the next call will have the left end as start and
the right end as mid.
- Each recursive call, generates a new range to search within.
Exercise 1:
Implement and modify the above the program to print out something
before every return statement in binarySearch().
This allows you to see what's going on.
Now consider the following problem:
- Consider the data
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- Suppose the search term were 300 (larger than the
largest value in the array) or 15 (smaller than the
smallest value).
- The code above does not explicitly check whether the search
term is inside the range of the elements in the array.
Does the code break down if you present it with a value outside the
range? Try it out and see what happens. Then explain what you see.
Here's an interesting variation:
public class BinarySearch2 {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = {24, 32, 41, 42, 51, 63, 71, 73, 85, 87};
// Create a test value to search for.
int searchTerm = 32;
// Note: initially, the "range" is 0,...,testData.length-1
boolean found = binarySearch (testData, searchTerm, 0, testData.length-1);
// Print result.
System.out.println ("found = " + found);
// Another search.
searchTerm = 55;
found = binarySearch (testData, searchTerm, 0, testData.length-1);
System.out.println ("found = " + found);
}
static boolean binarySearch (int[] A, int value, int start, int end)
{
// Only need to check if the interval got inverted.
if (start > end) {
return false;
}
// Find the middle:
int mid = (start + end) / 2;
if (A[mid] == value) {
return true;
}
else if (value <= A[mid]) {
// Search the left half: A[start],...,A[mid-1]
return binarySearch (A, value, start, mid-1);
}
else {
// Search the right half: A[mid+1],...,A[end]
return binarySearch (A, value, mid+1, end);
}
}
}
Note:
- It's a little difficult to see why this simpler bottom-out
condition works.
- It's easy to see how the recursion works for large
intervals:
- For a large interval, either the search value is equal to
A[mid] or not.
- If not, we know it's either strictly less (and therefore, we search
to the left), or strictly larger (and therefore, we search to to the right).
- However, it's not clear what happens when we get down to
small intervals.
- Let's look at a simple example:
A = [24, 32]
search value = 25
- Initially, start==0 and end==1, and thus, mid=0
⇒
Therefore, value > A[mid], and we end up taking the else
// ...
if (A[mid] == value) {
return true;
}
else if (value < A[mid]) {
return binarySearch (A, value, start, mid-1);
}
else {
// This is what we execute with mid=0, end=1
return binarySearch (A, value, mid+1, end);
}
- Then, the next call to binarySearch() will have
start==1 and end==1.
⇒
This means, mid=1, and therefore value < A[mid]
⇒
We execute the first call:
// ...
if (A[mid] == value) {
return true;
}
else if (value < A[mid]) {
// This is what we execute with mid=1, end=1
return binarySearch (A, value, start, mid-1);
}
else {
return binarySearch (A, value, mid+1, end);
}
- Then, the next call has start==1 and end==0
⇒
Now start > end and so we're done (not found).
- Thus, for small intervals, even with only one element, we
allow further searching that eventually bottoms out.
Exercise 2:
Download SearchComparison.java
and UniformRandom.java
and compare Binary Search to simple search.
The code you downloaded contains both search methods. What you need
to do is to add code to count the number of comparisons made
by each method. Try this for array sizes of 10, 100, 1000 and 10000.
Finally, let's examine a non-recursive (iterative) version of Binary
Search:
public class BinarySearch3 {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = {24, 32, 41, 42, 51, 63, 71, 73, 85, 87};
// Create a test value to search for.
int searchTerm = 32;
// Note: initially, the "range" is 0,...,testData.length-1
boolean found = binarySearch (testData, searchTerm);
// Print result.
System.out.println ("found = " + found);
// Another search.
searchTerm = 55;
found = binarySearch (testData, searchTerm);
System.out.println ("found = " + found);
}
static boolean binarySearch (int[] A, int value)
{
// Instead of calling the method recursively, we can also
// set start and end initially, and simply adjust the values
// in a loop.
int start = 0;
int end = A.length - 1;
while (start <= end) {
int mid = (start + end) / 2;
if (value == A[mid]) {
return true;
}
else if (value < A[mid]) {
end = mid-1;
}
else {
start = mid+1;
}
} // end-while
return false;
}
}
Note:
- The code is quite elegant and simple.
- What makes it simple is that we only need to adjust either
start or end each time.
- Generally, iterative versions are not simpler than recursive
versions, but Binary Search is probably an exception.
The power example revisited
We will revisit the power examples from Module 4:
- First, recall how we used recursion to compute powers:
public class PowerExample3 {
public static void main (String[] argv)
{
int p = power (3, 2);
System.out.println ( "3^2 = " + p);
p = power (3, 4);
System.out.println ( "3^4 = " + p);
p = power (2, 8);
System.out.println ( "2^8 = " + p);
}
static int power (int a, int b)
{
if (b == 0) {
return 1;
}
return (a * power (a, b-1));
}
}
- Using int's limits the size of powers we can compute.
⇒
For example, we can't compute 2127-1 (the
largest prime known in 1876)
To handle arbitrarily large integers, Java provides the
BigInteger class:
- One BitInteger instance is used for each number desired.
- The BigInteger class provides methods for the usual
operations: add, sub, multiple, divide.
Let's look at an example:
import java.math.*; // We need to import from this library.
public class BigIntegerExample {
public static void main (String[] argv)
{
// Create two instances with 5 and 2 as actual values.
BigInteger A = new BigInteger ("5");
BigInteger B = new BigInteger ("2");
// Examples of arithmetic operations:
BigInteger C = A.add (B); // 7
BigInteger D = A.multiply (B); // 10
BigInteger E = A.divide (B); // 2
BigInteger F = A.mod (B); // 1
System.out.println ("A=" + A + " B=" + B + " C=" + C + " D=" + D + " E=" + E + " F=" + F);
// Two constants.
BigInteger zero = new BigInteger ("0");
BigInteger one = new BigInteger ("1");
BigInteger G = A.add (zero); // 5
BigInteger H = B.multiply (one); // 2
System.out.println ("G=" + G + " H=" + H);
// Largest possible int.
int x = 2147483647;
int y = x*x; // "Garbage" result: it won't work.
System.out.println ("x=" + x + " y=" + y);
// But this works fine:
BigInteger X = new BigInteger ("2147483647");
BigInteger Y = X.multiply (X);
System.out.println ("X=" + X + " Y=" + Y);
// And now for some really large integers ...
// Some of the largest known primes in history, found without computers.
// Largest known in 1588, by P.Cataldi:
BigInteger P1 = new BigInteger ("524287");
// Next record in 1772, by Euler:
BigInteger P2 = new BigInteger ("2147483647");
// Then in 1876 by Lucas:
BigInteger P3 = new BigInteger ("170141183460469231731687303715884105727");
// Next record in 1951 by Ferrier:
BigInteger P4 = new BigInteger ("20988936657440586486151264256610222593863921");
}
}
Next, let's re-do our power example using BigInteger's:
import java.math.*;
public class BigPower {
public static void main (String[] argv)
{
// The first two examples, of course, can be done with int's.
BigInteger X = new BigInteger ("3");
BigInteger Y = new BigInteger ("2");
BigInteger Z = power (X, Y);
System.out.println (X + "^" + Y + " = " + Z);
X = new BigInteger ("2");
Y = new BigInteger ("8");
Z = power (X, Y);
System.out.println (X + "^" + Y + " = " + Z);
// But this one cannot be computed using int's.
X = new BigInteger ("2");
Y = new BigInteger ("1000");
Z = power (X, Y);
System.out.println (X + "^" + Y + " = " + Z);
}
// Some constants that will be useful below.
static BigInteger zero = new BigInteger ("0");
static BigInteger one = new BigInteger ("1");
static BigInteger power (BigInteger A, BigInteger B)
{
if ( B.equals(zero) ) {
return new BigInteger ("1");
}
// Recurse.
BigInteger BMinus1 = B.subtract (one);
BigInteger temp = power (A, BMinus1);
BigInteger P = A.multiply (temp);
// Thus, P = A*power(A, B-1)
return P;
}
}
Exercise 3:
Recall how compactly the power() method was written for the
case where we had int's:
static int power (int a, int b)
{
if (b == 0) {
return 1;
}
return (a * power (a, b-1));
}
Modify the BigInteger example above and do the same. The
result is probably less readable, but it's a good exercise to
see how it can be done.
Recursion and fractals
Next, let's look at an interesting use of recursion in drawing a
fractal:
- We will draw the so-called Von-Koch Snowflake (of a given
depth).
- Since fractals are themselves defined recursively, recursion
is very convenient to use as the programming method.
- Here, below are the snowflakes of depth=1, depth=2 and
depth=4, respectively.
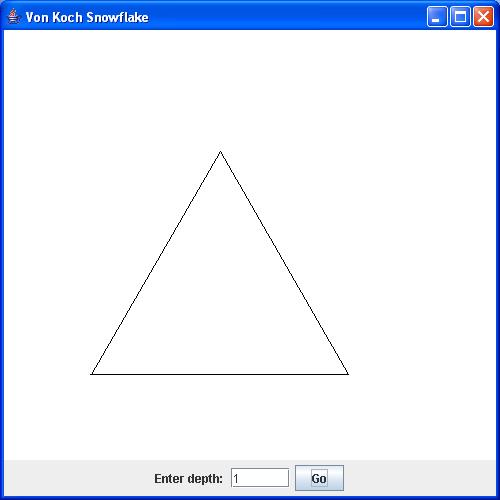
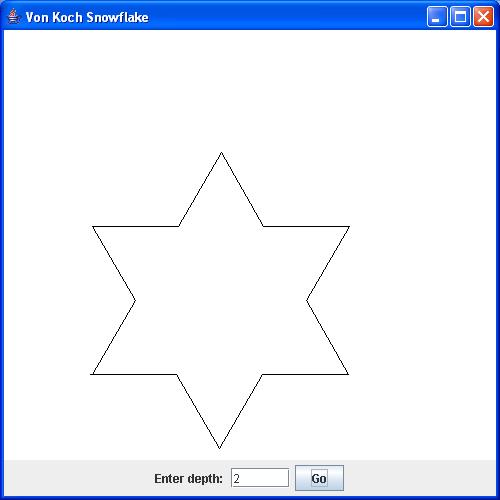

- Thus, at depth=1 each side is a line.
- When depth=2, the depth=1 side is a fractal consisting of
four parts, each of which is a line.
- Similarly, one recurses down until the given depth to
actually draw lines.
To implement:
- We will simply recurse downwards, changing the length of
the "fractal side" to be drawn
- This sounds simpler than it actually is. There are some
complexities:
- We will keep track of which segment we are drawing
relative to the previously drawn segment.
- To do this, we will compute the change in angle
going from one segment to another.
Here's the program:
import java.awt.*;
import java.awt.event.*;
import javax.swing.*;
import javax.swing.event.*;
class SnowflakePanel extends JPanel {
// These values will be used in the recursion.
int depth = 0;
double currentAngle;
// The end points of the current "fractal edge"
Point currentPoint, nextPoint;
// paintComponent is called whenever the screen needs to be rendered.
// This is where we do all our drawing work.
public void paintComponent (Graphics g)
{
super.paintComponent (g);
if (depth == 0) {
// We actually need this because there is nothing to draw
// when the screen first comes up.
return;
}
// Create a grey background and white pen color.
Dimension D = this.getSize();
g.setColor (Color.white);
g.fillRect (0,0, D.width, D.height);
g.setColor (Color.black);
// Now figure out an appropriate size for the length of
// the side of the initial triangle.
int minDim = D.width;
if (D.height < minDim) {
minDim = D.height;
}
int leftInset = (int) (0.2 * minDim);
double initLength = (int) (0.6 * minDim);
// The first point is a little inside the origin.
currentPoint = new Point (leftInset, leftInset);
// Start with initial angle horizontal.
currentAngle = 0;
// Draw three "fractal sides" next.
// The first one.
drawSide (initLength, depth, g);
changeAngleRight (120);
// After drawing the base, the next line comes at an angle of 120.
// Now the second one, after which there's another 120 rotation.
drawSide (initLength, depth, g);
changeAngleRight (120);
// Last one.
drawSide (initLength, depth, g);
}
void drawSide (double length, int depth, Graphics g)
{
if (length <= 1) {
// Too small: we can't draw something smaller than a pixel.
System.out.println ("Length too small: depth too much");
return;
}
// Base case:
if (depth == 1) {
// Compute next point by turning the angle and using the angle
// to compute the (x,y) values of the end-point.
nextPoint = new Point ();
double radians = currentAngle*Math.PI/180.0;
nextPoint.x = currentPoint.x + (int) (Math.cos(radians) * length);
nextPoint.y = currentPoint.y + (int) (Math.sin(radians) * length);
// Draw.
Dimension D = this.getSize();
g.drawLine (currentPoint.x, D.height-currentPoint.y, nextPoint.x, D.height-nextPoint.y);
// Update.
currentPoint = nextPoint;
return;
}
// Recursive case: draw FOUR sides fractally. After each, the angle
// needs to be changed to compute the new end-points.
drawSide (length/3, depth-1, g);
changeAngleLeft (60);
drawSide (length/3, depth-1, g);
changeAngleRight (120);
drawSide (length/3, depth-1, g);
changeAngleLeft (60);
drawSide (length/3, depth-1, g);
}
// Methods to set the angle.
void changeAngleRight (double increment)
{
currentAngle = currentAngle + increment;
}
void changeAngleLeft (double increment)
{
currentAngle = currentAngle - increment;
}
} //end-SnowflakePanel
// The remainder of the code is entirely GUI-related.
class SnowflakeFrame extends JFrame {
// A text field where the user enters the fractal depth.
JTextField depthField;
// The panel on which we draw.
SnowflakePanel drawPanel;
public SnowflakeFrame ()
{
this.setSize (500,500);
this.setTitle ("Von Koch Snowflake");
this.setResizable (true);
// This is how stuff is put into a frame.
Container cPane = this.getContentPane();
drawPanel = new SnowflakePanel ();
cPane.add (drawPanel, BorderLayout.CENTER);
// Make the controls.
JPanel panel = new JPanel ();
JLabel label = new JLabel ("Enter depth: ");
panel.add (label);
depthField = new JTextField (5);
panel.add (depthField);
JButton button = new JButton ("Go");
button.addActionListener (
new ActionListener () {
public void actionPerformed (ActionEvent a)
{
handleButtonClick();
}
}
);
panel.add (button);
cPane.add (panel, BorderLayout.SOUTH);
this.setVisible (true);
}
void handleButtonClick ()
{
// Extract the string from the textfield where the user typed the strings.
String inputStr = depthField.getText ();
try {
int d = Integer.parseInt (inputStr.trim());
drawPanel.depth = d;
drawPanel.repaint();
}
catch (NumberFormatException e) {
System.out.println (e);
}
}
}
public class Snowflake {
public static void main (String[] argv)
{
SnowflakeFrame s = new SnowflakeFrame ();
}
}
Exercise 4:
Download and execute the above program to see how it works.
© 2006, Rahul Simha (revised 2017)


