Module 3: Sorting
Supplemental material
Selection: a prelude to sorting
First consider the selection problem: finding the min and max
in an array:
import java.util.*;
public class FindExtremes {
public static void main (String[] argv)
{
// Fill an array with some random values - for testing.
int[] testData = makeRandomArray (10);
// Find largest and smallest elements.
int smallest = findSmallest (testData);
int largest = findLargest (testData);
// Print.
System.out.println ("Smallest=" + smallest + ", largest=" + largest + " in array " + Arrays.toString(testData));
}
static int findSmallest (int[] A)
{
// Start by assuming first is smallest.
int smallest = A[0];
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
}
}
return smallest;
}
static int findLargest (int[] A)
{
// Similar to findSmallest except for if-condition.
int largest = A[0];
for (int i=1; i < A.length; i++) {
if (A[i] > largest) {
largest = A[i];
}
}
return largest;
}
static int[] makeRandomArray (int length)
{
int[] A = new int [length];
for (int i=0; i < A.length; i++) {
A[i] = UniformRandom.uniform (1, 100);
}
return A;
}
}
In-Class Exercise 1:
Download the above program
(You'll also need UniformRandom.java)
and modify it to also print the positions in the array where
the min and max occur. For example,
Smallest=24 at position=1, largest=87 at position=8 in array [51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
Let's examine a variation of the program written for
String's:
import java.util.*;
public class FindStringExtremes {
public static void main (String[] argv)
{
// Some test data (a subset of Java's reserved words).
String[] reservedWords = {"if", "else", "while", "do", "return",
"true", "false", "instanceof", "class"};
// Here, smallest means 'alphabetically first'.
String smallest = findSmallest (reservedWords);
String largest = findLargest (reservedWords);
// Print.
System.out.println ("Smallest=\"" + smallest + "\", largest=\"" + largest + "\" in array " + Arrays.toString(reservedWords));
}
static String findLargest (String[] words)
{
String largest = words[0];
for (int i=1; i < words.length; i++) {
// Note: compareTo() method in String returns an int.
if ( words[i].compareTo (largest) > 0 ) {
largest = words[i];
}
}
return largest;
}
static String findSmallest (String[] words)
{
String smallest = words[0];
for (int i=1; i < words.length; i++) {
if ( words[i].compareTo (smallest) < 0 ) {
smallest = words[i];
}
}
return smallest;
}
}
Note:
- The class String has a compareTo() method
that when invoked as str1.compareTo(str2)
returns -1 if str1
comes alphabetically before str2
returns 1 if str1
comes alphabetically after str2
returns 0 if the two strings are equal
- In all other respects, the program is like the one for
integer arrays.
Next, let's return to the integer example and:
- Find the smallest element.
- Then place the smallest element in the first position in the
array.
- Whatever was in the first position gets moved to where the
smallest one was found.
Here's the program:
import java.util.*;
public class SmallestInFront {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
smallestInFront (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void smallestInFront (int[] A)
{
// Start by assuming first is smallest.
int smallest = A[0];
// We're going to record the position where the smallest occurs.
int pos = 0;
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in front.
int temp = A[0];
A[0] = A[pos];
A[pos] = temp;
}
static int[] makeRandomArray (int length)
{
// ... same as before ...
}
}
In-Class Exercise 2:
Modify the above idea to put the largest element at the back
(last position) of the array, and do this for String arrays.
Download LargestAtBack.java and
implement the method largestAtBack().
Now let's examine a small variation: we'll place the smallest
two elements at the front:
import java.util.*;
public class SmallestInFront2 {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
smallestTwoInFront (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void smallestTwoInFront (int[] A)
{
// First, the smallest in front.
int smallest = A[0];
int pos = 0;
// Check against A[1], A[2] ... etc.
for (int i=1; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in front.
int temp = A[0];
A[0] = A[pos];
A[pos] = temp;
// Now for the second smallest: put that in A[1].
smallest = A[1];
pos = 1;
// Check against A[2], A[3] ... etc.
for (int i=2; i < A.length; i++) {
if (A[i] < smallest) {
smallest = A[i];
pos = i;
}
}
// Swap with what's in A[1].
temp = A[1];
A[1] = A[pos];
A[pos] = temp;
}
static int[] makeRandomArray (int length)
{
// ... same as before ...
}
}
In-Class Exercise 3:
Here's some sample output for the above program:
Before: [51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
After: [24, 32, 63, 73, 42, 85, 71, 41, 87, 51]
Explain how '51' reached the last position in the array.
We'll now extend this idea to create our first sorting algorithm.
Selection sort
The idea behind Selection Sort is simple:
- Find the smallest element and put that in the first array position.
- Find the second smallest, and put that in the second position.
- Find the third smallest, ... etc.
Here's the program:
import java.util.*;
public class SelectionSort {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
selectionSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void selectionSort (int[] A)
{
// We don't need to find the n-th smallest, so stop at n-1.
for (int i=0; i < A.length-1; i++) {
// Find i-th smallest and swap.
int smallest = A[i];
int pos = i;
// Look from i+1 and up.
for (int j=i+1; j < A.length; j++) {
if (A[j] < smallest) {
smallest = A[j];
pos = j;
}
}
// Swap into position i.
int temp = A[i];
A[i] = A[pos];
A[pos] = temp;
}
}
static int[] makeRandomArray (int length)
{
// ...
}
}
In-Class Exercise 4:
Download the above program
and modify it so that the largest element
is placed at the back, then the second largest is placed in the
second-last position in the array, ... and so on.
Bubble sort
The key ideas behind Bubble Sort:
- Bubble-sort performs several sweeps starting from the end
of the array.
- In each sweep, we swap neighboring elements out of order.
- If we perform enough sweeps, the array will end up sorted.
Let's look at the code:
import java.util.*;
public class BubbleSort {
public static void main (String[] argv)
{
int[] testData = makeRandomArray (10);
System.out.println ("Before: " + Arrays.toString(testData));
bubbleSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void bubbleSort (int[] A)
{
// Each sweep, i=0...n-1, will put the i-th least element in place.
for (int i=0; i < A.length-1; i++) {
// Perform swaps from end-of-array down to i-th position.
for (int j=A.length-1; j>i; j--) {
if (A[j] < A[j-1]) {
// Out of order: swap needed.
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
}
static int[] makeRandomArray (int length)
{
// ...
}
}
To see how it works in a little more detail,
let's sort the
array [40, 30, 10, 50, 20]:
Sweep for i=0:
Comparison at position j=4: 40 30 10 50 20 // Need to swap 20 and 50
Comparison at position j=3: 40 30 10 20 50
Comparison at position j=2: 40 30 10 20 50 // Need to swap 10 and 30
Comparison at position j=1: 40 10 30 20 50 // Need to swap 10 and 40
Sweep for i=1:
Comparison at position j=4: 10 40 30 20 50
Comparison at position j=3: 10 40 30 20 50 // Need to swap 20 and 30
Comparison at position j=2: 10 40 20 30 50 // Need to swap 20 and 40
Sweep for i=2:
Comparison at position j=4: 10 20 40 30 50
Comparison at position j=3: 10 20 40 30 50 // Need to swap 30 and 40
Sweep for i=3:
Comparison at position j=4: 10 20 30 40 50
Insertion sort
We'll lead up to Insertion-Sort through a couple
of examples.
First, consider this idea:
- We'll create a separate array that will contain the sorted elements.
- To create the sorted array, we go through the original and
copy over the current element "into the right place" in the sorted array.
- For example, suppose array A is to be sorted:
- We'll created a sorted version in array B.
- Here are the first few elements when we start:
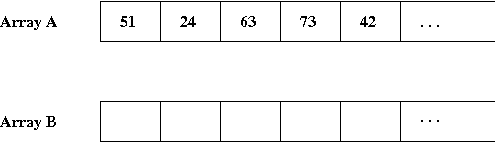
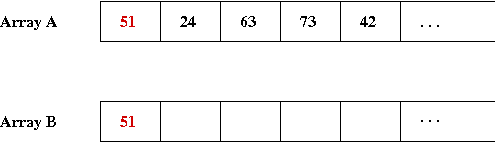
- The first element to insert in B is '51', which gets
into the first spot in B:
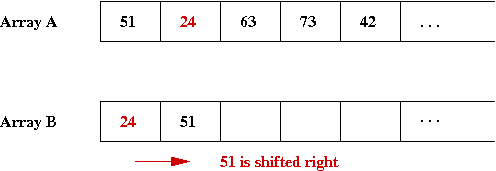
- Next element to insert is '24', for which we need to shift
'51' in the B array
⇒ We'll keep B sorted.
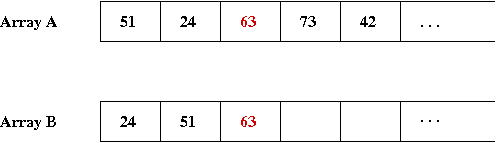
- Next element is '63', which goes into the 3rd spot:
- Then '73':
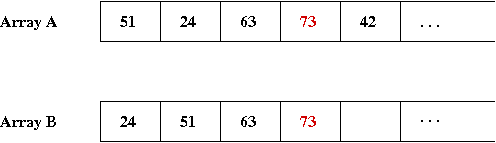
- Finally, for '42', we need to shift-right three elements to
find the right place for '42':
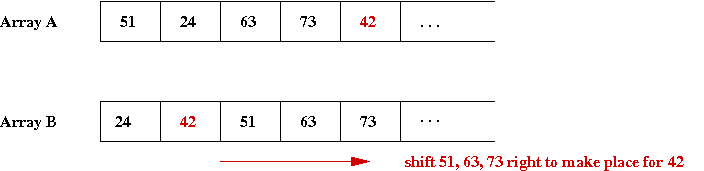
- Thus, the general idea is:
- Proceed sequentially through A's elements.
- For each, find the right place in B, shifting right
as necessary.
Here's the program:
import java.util.*;
public class InsertionSort1 {
public static void main (String[] argv)
{
int[] testData = {51, 24, 63, 73, 42, 85, 71, 41, 87, 32};
System.out.println ("Before: " + Arrays.toString(testData));
int[] sortedData = insertionSort (testData);
System.out.println ("After: " + Arrays.toString(sortedData));
}
static int[] insertionSort (int[] A)
{
// Make space for the "result" array B:
int[] B = new int [A.length];
// Go through A's elements and find the right place for each in B:
for (int i=0; i < A.length; i++) {
// Find the right place for A[i] in array B.
int posInB = i;
for (int j=0; j < i; j++) {
if (B[j] < A[i]) {
// Skip.
}
else {
posInB = j;
break;
}
}
// Now shift rightwards in B from posInB onwards.
for (int j=i+1; j>posInB; j--) {
// We need this because the array has to be shifted except
// for the last position when i=n-1.
if (j < B.length) {
B[j] = B[j-1];
}
}
// Assign A[i] in right place.
B[posInB] = A[i];
}
return B;
}
static int[] makeRandomArray (int length)
{
// ...
}
}
Note:
- To find the right place in B:
- We start at the right end of B (the most recent
index is i.
- We scan backwards, going past all elements that are larger
than A[i].
- When we find the right place:
- We shift-right all elements we skipped over.
- Then we insert A[i].
Now for the first clever insight:
- When we scan backwards in B, we can combine that
with shifting right
⇒
This is because we the elements we skip over need to be shifted right.
Let's re-write insertionSort() to do that:
static int[] insertionSort (int[] A)
{
int[] B = new int [A.length];
for (int i=0; i < A.length; i++) {
B[i] = A[i];
// Start at rightmost element in B.
int j = i;
// Swap as we go backwards.
while ( (j > 0) && (B[j] < B[j-1]) ) {
int temp = B[j];
B[j] = B[j-1];
B[j-1] = temp;
j --; // Mustn't forget the decrement.
}
}
return B;
}
Now the really clever insight:
- We don't need a separate array at all!
- After all, those elements we are skipping/swapping are precisely
those "to the left" in B
⇒
But these are the same "to-the-left" elements in A!
Here's a re-write of insertionSort() using only array A:
static void insertionSort (int[] A)
{
for (int i=0; i < A.length; i++) {
// Find the right place for A[i].
int j = i;
while ( (j > 0) && (A[j] < A[j-1]) ) {
// Swap until we stop.
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
j --;
}
}
}
Finally, we point out that a for-loop could be used instead
of the while-loop:
static void insertionSort (int[] A)
{
for (int i=0; i < A.length; i++) {
for (int j=i; (j>0) && (A[j] < A[j-1]); j--) {
int temp = A[j];
A[j] = A[j-1];
A[j-1] = temp;
}
}
}
In-Class Exercise 5:
Modify each of
SelectionSort.java,
BubbleSort.java
and
InsertionSort.java
to count the total number of comparisons made. That is:
- Each time two elements are compared for their "size", count
that as one comparison.
- Modify each file separately.
- Print the total number of comparisons required for
SelectionSort, the total required for BubbleSort and the
total required for InsertionSort.
Get this working for an array size of 10 elements. Then, get
the number-of-comparisons for a 20-element array, then 30, ...,
until 100. Plot a graph (by hand, on paper)
of the number of comparisons vs. array size.
Sorting our own objects
Let's look at an example where we create objects of our own design and
sort them:
Here's the program:
class Person {
// Some data:
String firstName;
String lastName;
int birthYear;
// This is called a constructor:
public Person (String firstName, String lastName, int birthYear)
{
this.firstName = firstName;
this.lastName = lastName;
this.birthYear = birthYear;
}
// A comparison method to allow two Person instances to be compared.
public boolean lessThan (Person p)
{
// Compare the birthyear inside this instance (where we are executing)
// with the birthyear of the parameter instance.
if (birthYear < p.birthYear) {
return true;
}
else {
return false;
}
}
} // end-of-Person
public class ObjectSortExample {
public static void main (String[] argv)
{
// Make space for 10 person pointers.
Person[] someKennedys = new Person [10];
// Each array location is itself an object pointer. We
// need to assign actual object instances using the new operator.
someKennedys[0] = new Person ("Patrick", "Kennedy", 1858);
someKennedys[1] = new Person ("Joseph", "Kennedy", 1888);
someKennedys[2] = new Person ("Rose", "Fitzgerald", 1890);
someKennedys[3] = new Person ("Joseph", "Kennedy", 1915);
someKennedys[4] = new Person ("John", "Kennedy", 1917);
someKennedys[5] = new Person ("Jacqueline", "Bouvier", 1929);
someKennedys[6] = new Person ("Robert", "Kennedy", 1925);
someKennedys[7] = new Person ("Edward", "Kennedy", 1932);
someKennedys[8] = new Person ("Caroline", "Kennedy", 1957);
someKennedys[9] = new Person ("Maria", "Shriver", 1955);
System.out.println ("Unsorted: ");
print (someKennedys);
sort (someKennedys);
System.out.println ("\nSorted: ");
print (someKennedys);
}
static void print (Person[] people)
{
for (int i=0; i < people.length; i++) {
System.out.println (people[i].firstName + " " + people[i].lastName + " (b. " + people[i].birthYear + ")");
}
}
static void sort (Person[] people)
{
// Selection Sort.
for (int i=0; i < people.length-1; i++) {
Person min = people[i];
int pos = i;
for (int j=i+1; j < people.length; j++) {
// Compare j-th person with best so far.
if ( people[j].lessThan (min) ) {
min = people[j];
pos = j;
}
}
// Swap.
Person temp = people[i];
people[i] = people[pos];
people[pos] = temp;
}
}
} // end-of-ObjectSortExample
Note:
- In the int version of Selection-Sort, the key
comparison occured in the for-loop:
for (int j=i+1; j < A.length; j++) {
if (A[j] < smallest) {
smallest = A[j];
pos = j;
}
}
Here, A[i] (an int) is compared to
smallest (also an int).
- In the Person example,
for (int j=i+1; j < people.length; j++) {
if ( people[j].lessThan (min) ) {
min = people[j];
pos = j;
}
}
Here, people[j] (a Person instance) is
compared to min (also a Person instance).
- The comparison itself is done inside the method
lessThan() in one instance.
Quicksort
Key ideas in Quicksort:
- Consider the array
[51, 24, 63, 73, 42, 85, 71, 41, 87, 32]
and the first element '51'.
- Suppose we place the elements less than '51' to the left
and those greater to the right of it:
[24, 42, 41, 32] 51 [63, 73, 85, 71, 87]
- Then, suppose we magically sort the left array independently:
[24, 32, 41, 42] 51 [63, 73, 85, 71, 87]
- Next, suppose we magically sort the right array:
[24, 32, 41, 42] 51 [63, 71, 73, 85, 87]
- Then, we can piece together the final result:
[24, 32, 41, 42, 51, 63, 71, 73, 85, 87]
- Key insight: sorting the smaller arrays (left and right)
is just like sorting a larger array
⇒
We can apply the same idea recursively.
- Thus, the code is going to look like this:
static void quickSortRecursive (int[] data, int left, int right)
{
if (left < right) {
// Partition to find the "right place" for the leftmost element.
int partitionPosition = quickSortPartition (data, left, right);
// Recurse on the left side:
quickSortRecursive (data, left, partitionPosition-1);
// Recurse on the right side:
quickSortRecursive (data, partitionPosition+1, right);
}
// Else: left==right so we're done.
}
- We won't need to build separate arrays if we can somehow
do everything in one array:
- When we "partition" the array, we use the leftmost element
and find the "right place" for it:
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^
partition position = 4
- Then, all we need are the limits on each side:
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^ ^ // Left array limits
left=0 right=3
and
[24, 42, 41, 32, 51, 63, 73, 85, 71, 87] // Inside original array
^ ^ // Right array limits
left=6 right=9
- Thus, if we can write the recursive method to work with "left"
and "right" indices to delineate a portion of the array, we can use
the same array.
Here's the program:
import java.util.*;
public class QuickSort {
public static void main (String[] argv)
{
int[] testData = {51, 24, 63, 73, 42, 85, 71, 41, 87, 32};
System.out.println ("Before: " + Arrays.toString(testData));
quickSort (testData);
System.out.println ("After: " + Arrays.toString(testData));
}
static void quickSort (int[] A)
{
quickSortRecursive (A, 0, A.length-1);
}
static void quickSortRecursive (int[] data, int left, int right)
{
if (left < right) {
// Partition to find the "right place" for the leftmost element.
int partitionPosition = quickSortPartition (data, left, right);
// Recurse on the left side:
quickSortRecursive (data, left, partitionPosition-1);
// Recurse on the right side:
quickSortRecursive (data, partitionPosition+1, right);
}
// Else: left==right so we're done.
}
static int quickSortPartition (int[] data, int left, int right)
{
if (left == right)
return left;
int partitionElement = data[right];
int currentSwapPosition = right;
for (int i=right-1; i>=left; i--) {
// Examine everything between left and right-1 inclusive.
if (data[i] > partitionElement) {
// Switch with swap position
currentSwapPosition--;
swap (data, currentSwapPosition, i);
// Shift swap position rightwards:
}
}
// Last one:
swap (data, currentSwapPosition, right);
return currentSwapPosition;
}
static void swap (int[] data, int i, int j)
{
int temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
In-Class Exercise 6:
Can you identify where in the code comparisons are actually made?
Modify QuickSort2.java to count the
number of comparisons. Then plot the results along with the
other sort algorithms in Exercise 5 above.
Measuring actual run time
In Java, it is fairly easy to measure actual running time, accurate
to within milliseconds, for example:
// Get the current time (in milliseconds).
long startTime = System.currentTimeMillis ();
// Here's the code we're going to evaluate.
selectionSort (A);
// After it has run, we record the time taken as the current
// time minus the starttime.
long timeTaken = System.currentTimeMillis () - startTime;
System.out.println ("Selection sort time: " + timeTaken);
In-Class Exercise 7:
Download and execute SortPerformance.java
to compare QuickSort with SelectionSort.
Do either InsertionSort or BubbleSort compare with QuickSort?
Copy over those algorithms and try it out.
© 2006, Rahul Simha (revised 2017)





