int[] A = {1, 2, 7, 9, 18, 29, 32, 41};
The sequence of numbers in this array is always increasing.
Similarly, the array
int[] B = {38, 24, 18, 12, 8, 3};
is a decreasing sequence of integers.
We will call such arrays monotonic arrays.
This property does not hold for the array
int[] C = {1, 2, 7, 3, 18, 14, 32, 41};
Here, after initially increasing numbers 1, 2, 7, the
fourth one, 3, is less than 7. This array is neither
always increasing nor always decreasing, and is
therefore not monotonic.
Write a program called
CheckMonotonic.java
that takes an array and prints either "Monotonic"
nor "Not monotonic", depending on whether the
array is monotonic. Test your program with the
above three arrays.
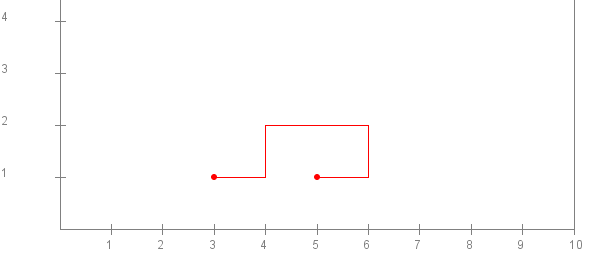
We will use the numbers 1,2,3,4 to represent the four directions North, East, South, West. Then, the walk that that goes East, North, East, East, South, West is represented by the numbers 2,1,2,2,3,4.
Here are the numbers in an array with the
starting point (3,1):
double x=3, y=1;
double[] A = {2, 1, 2, 2, 3, 4};
Clearly, after starting at (3,1)
and following these "directions", we end up at
(5,1).
One can use DrawTool to depict this "integer walk":
Write a program called
IntegerWalk
that takes a starting point and
an array of "directions" like above and draws the walk.
Test your program with the above data, and then get it working
for this starting point and array:
double x=1, y=9;
double[] A = {3,2,3,3,2,1,2,3,3,3,2,2,1,2,1,2,3,3,3,4,3};
Note: although our points are actually integer values, we will use
double
variables (and arrays) for consistency with
DrawTool.
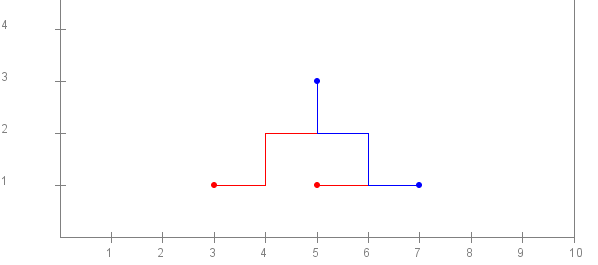
double x1=3, y1=1;
double[] A = {2, 1, 2, 2, 3, 4};
double x2=5, y2=3;
double[] B = {3, 2, 3, 2};
When drawn in red and blue, we see that there are
two segments in common:
Write a program called CommonSegments
to print out the common segments when given two
integer walks (two starting points, and two
direction arrays, as above). Your program
should print out the common segments. For example,
for the above two walks, the output should be
2 segments:
(5.0,2.0)-(6.0,2.0)
(6.0,2.0)-(6.0,1.0)
Test your program on both the small example
above and the longer walks
double x1=1, y1=9;
double[] A = {3,2,3,3,2,1,2,3,3,3,2,2,1,2,1,2,3,3,3,4,3};
double x2=2, y2=2;
double[] B = {1,2,1,2,3,2,1,2,2,2,2,1,1,4,4,4,1,1,2};