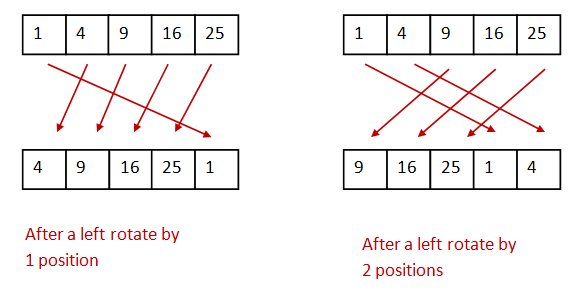
Here, elements are shifted leftwards, and an element that is shifted "off the left end" is shifted into the rightmost position. We have described a left rotation by 1 position (each element gets shifted by one spot). One can generalize this to a rotation in which each element moves k spots to the left. An example with k=2 is shown above.
Write a program called LeftRotate.java that achieves a left rotation of the array int[] A={1,4,9,16,25}.
Then, write a program called LeftRotateByK.java that achieves a left rotation of the array int[] A={1,4,9,16,25} by k positions, where k is a variable you can change in the program. Test it out for k=2, k=3 and k=5.
int[] histogram = {2, 3, 8, 2, 1, 0, 3, 0, 6, 3};
Think of the elements in here as the heights of rectangles
that will be drawn along the x-axis using
DrawTool
as shown below:
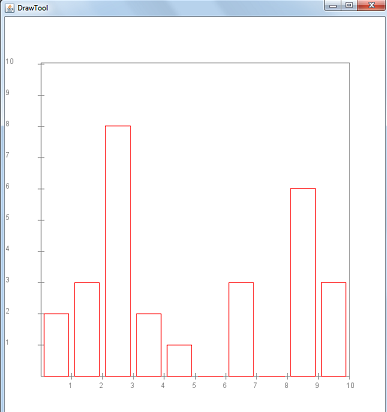
Such a picture is called a histogram. Write a program called Histogram.java that takes the histogram array and draws the rectangles. Don't forget that the width of each rectangle is slightly less than 1.0 and that you need DrawTool.java in the same directory.
double[] data = {8.5, 6.6, 2.7, 2.1, 9.4, 0.9,
2.1, 6.2, 8.3, 1.2, 2.2, 0.3,
9.3, 2.6, 3.8, 2.5, 6.8, 8.1,
8.8, 9.5, 1.8, 8.2, 1.5, 2.9,
8.9, 3.1, 2.9, 4.6};
The above data was used to count how many data values
are in the range 0 to 1 (answer: 2), how
many in the range 1 to 2 (answer: 3), etc.
Thus, this is the data used to generate the histogram
counts in the previous exercise.
Write a program called
HistogramGeneration.java
that takes the
data
array, uses it to generate a corresponding
histogram
array and draws the rectangles.