Module 7: Real Numbers

Objectives

By the end of this module, for simple programs with real numbers, you will be able to:

Create variable declarations for variables.
Assign values to variables by simple assignment, and print them out.
Demonstrate ability to perform operations for a desired output.
Evaluate expressions with variables in them.
Convert English descriptions of operations into expressions.
Mentally trace execution with expressions and calculations.
Mentally trace expressions and calculations inside for-loops.
Produce desired output using for-loops and calculations.
Identify new syntactic elements related to the above.

Real-valued variables

Just like we did with integers, we can declare variables and assign values to them:

Another example:

Again, as with integers, the standard operators apply:

In-Class Exercise 1: Write a program to print out the area of a circle whose radius is 1.5 inches.

In-Class Exercise 2: Can you find a well-known formula or law in science or engineering that uses all four of the standard operators: +, -, *, /? If not, find one that uses as many as possible.

In-Class Exercise 3: Do the increment and decrement operators work with real numbers?

Now consider this simple example:

In-Class Exercise 4: Change the assignment to:

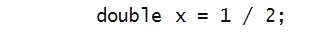
and see what prints. Explain the result.

Real-valued variables in loops

Let's write a program to sum the numbers 0.1, 0.2, ..., 1.0.

Here's one way:

In-Class Exercise 5: Use a table to trace the execution of the above loop. Show the changing values of sum, x, and i.

We'll now examine a number of variations:

We can use real variables directly in the for-loop:
Here's the same example with shortcut operators:

Next, consider this product computation:

In-Class Exercise 6: Do you recognize what the above loop is computing? Edit, compile and execute to see the output.

In-Class Exercise 7: Modify the above program to compute the product of numbers 0.1 * 0.2 * ... * 1.0. What do you observe as the output that is inconsistent with the product in the previous exercise? What is the explanation?

An example with a nested loop

Let's write a program to explore the sum 1 + (1/2) + (1/2)² + ... + (1/2)ⁿ.

Let's do this in steps:

First, some pseudocode at the highest level:

      sum = 0
      for k=0 to n {
         x = (1/2) raised-to-power k
         sum = sum + x
      }
      Print sum

But (1/2)^k = (1/2) * (1/2) * ... * (1/2) (k-times).
=> This is itself a loop.
Let's first write the inner loop for fixed k:

In-Class Exercise 8: Try this out to see that it works.

We'll now put this into the larger loop for the sum.

In-Class Exercise 9: Trace the execution using a table, with changing values of sum, k, power and i.

In-Class Exercise 10: Does this program work for the corner cases of n=0 and n=1?

In-Class Exercise 11: Explore what you get for larger values of n. Can you write the sum mathematically and determine the limiting value (as n→∞)?

Casting

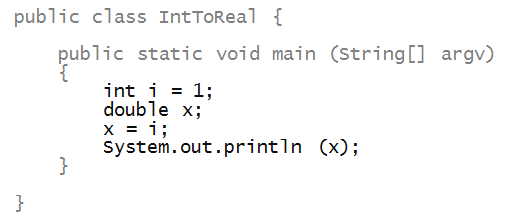
Consider the following program:

In-Class Exercise 12: What you suppose will be printed? Try it. Then, change the program so that you initially assign the value of 1 to i and then assign i to x.

An assignment from an int to a double works fine:

About casting:

The assignment from int to double works because every int is a valid double value.
However, a double need not be a valid int.
=> Which is why the compiler complains.
However, we can force an assignment using an explicit cast (jargon alert!)
The result: the largest integer less than the real.
=> The result is 1 above.
An explicit cast is need even if the double's value happens to be an integer like 1.0.
As we'll see later, casting is a general operation that can be applied to different variable types.

In-Class Exercise 13: What do you get when you cast the real value 0.5 to an int?

Reading and writing

Consider this somewhat complex program:

We'll read this program in steps:

First, observe that a variable called sum is declared, stuff gets added to it, and then it gets printed:
Now let's read the outermost loop:
- Here, we notice that a loop variable called x "drives" the loop.
- Note the start, end, and increment.
- Make sure your eyes catch the closing brace (bracket) of the outer loop.
So far, so good.
Next, look at the next level:
- The loop "driver" is variable y.
- Note the start, end and increment.
- Observe also that y is used not only in the calculation, but as part of the condition for the innermost loop.
Next, we see that there is a variable declared and used entirely within this loop:
(To save space, we've only shown the code inside main).
- Here, you say to yourself: "There's a variable that's initialized to 1, then it multiplicatively accumulates stuff, and gets added to sum."
Now for the innermost loop:
- This loop is driven by z.
- Notice that the start value depends on the current value of y.
- Thus, each time we do the innermost loop will be different because y changes.

When writing nested for-loops:

Write the first line of outermost loop and the closing brace:
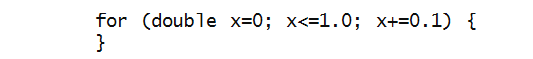
Then, back up into the body and write the code inside:
... and so on.

In-Class Exercise 14: Armed with your improved reading skills and added knowledge of syntax, go back to Module 0 and read through the first primes program. Examine the for-loops in particular - you should be able to trace through them.

When things go wrong

In-Class Exercise 15: What is the bug in this program written to compute the sum of numbers 0.01, 0.02, ..., 0.1?

In-Class Exercise 16: What about this one? (We've shown only the code inside main.)

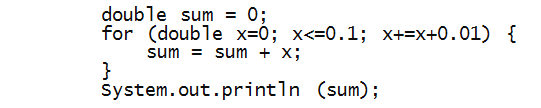
In-Class Exercise 17: What is the bug in this program written to compute the product of numbers 1, 2, ..., 10?