Module 6: Integers

Objectives

By the end of this module, for simple HelloWorld-like programs, you will be able to:

Create variable declarations.
Assign values to variables by simple assignment, and print them out.
Distinguish between integers in strings versus actual integers.
Demonstrate ability to perform operations on integers for a desired output.
Simplify expressions with constants to single value.
Evaluate expressions with variables in them.
Convert English descriptions of operations into expressions.
Mentally trace execution with expressions and calculations.
Mentally trace expressions and calculations inside for-loops.
Produce desired output using for-loops and calculations.
Identify new syntactic elements related to the above.

First, an analogy

Suppose we have boxes. Consider the following rules about "boxes":

Each box can store only one item.
The possible things that can be stored inside are called values.
Thus, at any given moment, a box's value is whatever's inside it.
Each box is "typed"
=> What this means:
- A box meant for shoes is allowed to store only shoes.
- A box meant for caps is allowed to store only caps.
Each box has a unique name:
There is a cloning process that works like this:
- The value inside one box is cloned.
- The cloned value is placed inside another.
There is a strange shortcut notation to specify cloning:
- Here, the = (equals sign) does not mean "equals."
- It has been repurposed to mean "clone", "copy," or, in programming-language jargon "assign".
Usage: "x is assigned the value in y".

In-Class Exercise 1: Suppose z is a box that stores caps. What will the statement z = y result in? Draw a picture.

Integer variables

Consider the following program:

In-Class Exercise 2: Edit, compile and execute the above program.

Now let's examine key parts of this program:

First, i is the name of a "box" (of sorts).
The term used for "box" is variable.
=> i is a variable.
Variables must be "typed"
=> i can only store integers.
To create and name a variable, we use a variable declaration:
Here, int is a reserved word in Java.
To put something in a variable, we use assignment
=> with the repurposed = (equals) sign.
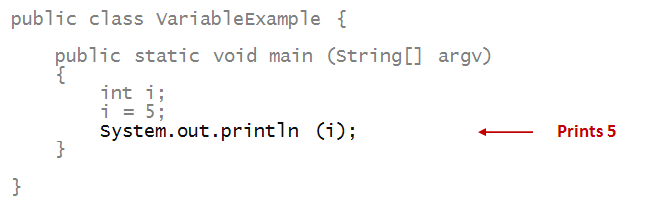
When we print a variable, what gets printed is its value.
=> Thus, the number 5 gets printed

Next, let's look at assignment between variables:

This is the analogue of cloning.
Consider this addition to the above program:
We say, in short, "i is assigned to j".

In-Class Exercise 3: What happens if you don't place a value in a variable? Find out by editing and compiling this program:

In-Class Exercise 4: Identify the output of this program just by reading (mental execution).

In-Class Exercise 5: Identify the output of this program just by reading

A rule: a variable must be declared before it is used (assigned a value or have a value copied from it).

In-Class Exercise 6: What is the compiler error you get for this program?

Variations

The following variations are worth knowing:

Comma-separated declarations:
Note: variables need not be declared in the order they are used in the program.
Declaration and assignment can be combined:
Another example:

In-Class Exercise 7: Consider the following partially-complete program:

Write code where indicated to have the program first print 6, then 5 (without changing the print statements).

Note writing style:

A space on either side of the equals sign for assignment.
The same when you combine declaration and assignment for a single variable.
It's customary to remove the space for multiple declarations.

Integer operators

First, let's consider some unary operators:

These are operators that apply to a single variable.
For example:
The unary operators here are the ++ (increment) and -- (decrement):
Note writing style: no space between variable and unary operator, but this is also acceptable:

In-Class Exercise 8: Mentally execute this program - what does it print?

Next, let's examine the familiar binary operators +, -, *, /

Addition: +
Subtraction: -
Multiplication: *
Division: /
Consider this example with addition:
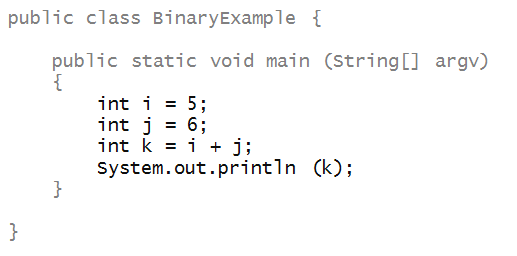
What happens during execution:
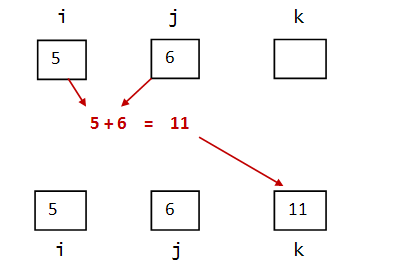
- The values in i and j are added.
- The resulting value goes into variable k.
A long-ish way of saying this aloud:
=> "k is assigned the sum of the values of i and j"
A shorter way:
=> "k is assigned i plus j"
Here's an example with multiplication and division:

In-Class Exercise 8: What does it print?

Expressions and operator-precedence

Consider the following program:

In-Class Exercise 9: What does it print?

About expressions:

An expression combines constants (like 1, above), and variables using operators.
Example:
i*j - (i+1)*(j-1).
The above expression is really equivalent to:
(i*j) - ((i+1) * (j-1)).
Here, we added some clarifying parentheses.
Operator precedence allows us to reduce the number of clarifying parentheses.
Java precedence follows standard predence in math: /, *, +, -.
The above expression is NOT the same as:
i*j - i+1*j-1.

In-Class Exercise 10: What does the expression i*j - i+1*j-1 evaluate to when i=7 and j=3?

Problem solving and pseudocode

Suppose we were given the following problem: write a program to print the first N odd numbers.

We'll solve it in the following steps:

First, let's sketch out a "program-like" outline (not a real program):

       N = 10                 // Let's make it work for N=10.
       for i=1 to N {
          Make the i-th odd number
          Print it
       }

This kind of rough outline is called pseudocode
=> We're meant to do this on paper, prior to programming.
Pseudocode looks a little like code, but is half-English.
For any given i, the i-th odd number is:
2*i - 1.
Now let's put this together into a program:

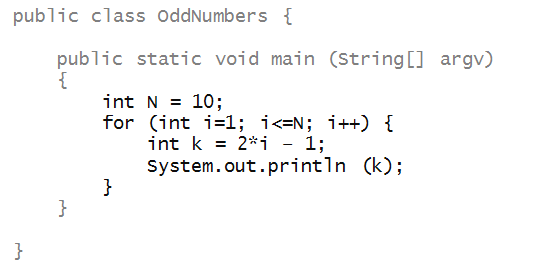
In-Class Exercise 11: Trace on paper the values of i and k in the program above. This is what you should be able to do mentally during mental execution.

More about expressions and assignment

Here are two more operators, one unary (negative sign) and one binary (remainder or mod operator), that are commonly used:

In-Class Exercise 12: What does it print?

In-Class Exercise 13: What does the following program print?

Now we'll look at a strange (initially) but very useful type of assignment:

Consider this program:
Prior to evaluating the expression, i has value 7.
On the right side, the current value of i is used to evaluate the expression.
=> Thus, the expression evaluates to (7 + 7/2) = 10.
This evaluated value then goes into variable i.
=> After the assignment, i has the value 10.

Let's use this to compute the sum of numbers from 0 to 10:

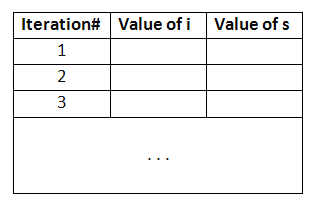
In-Class Exercise 14: Trace the changing values of s in the above program using the following table:

More problem-solving examples

Next, we'll look at some well-known ideas from mathematics, expressed in programs.

The first one is Fibonacci numbers.

The Fibonacci sequence is this:
0, 1, 1, 2, 3, 5, 8, 13, ...
Thus, the next Fibonacci number is the sum of the previous two.
Fibonacci numbers have proven useful in modeling biological growth, and have interesting mathematical properties.
Let's write a program to print Fibonacci numbers.
Observe: to compute a single Fibonacci number
=> We'll need a variable for it.
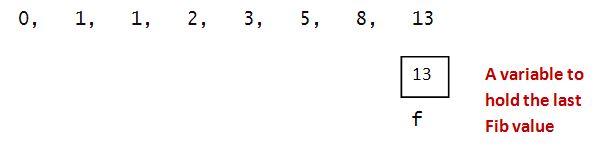
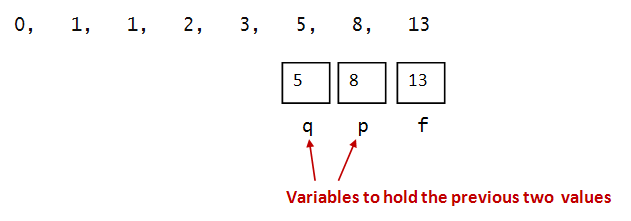
To compute this, we'll need variables for the previous two:

Let's start with some pseudocode:

       N = 10                 // We'll go up the N-th Fibonacci #
       p = 1                  // Initial value of p
       q = 0                  // Initial value of q
       for i=3 to N {
          Make the i-th Fibonacci number
          Print it
          Update p and q
       }

We're going to resist the temptation to code, and instead refine the pseudocode:

       N = 10                 // We'll go up the N-th Fibonacci #
       p = 1                  // Initial value of p
       q = 0                  // Initial value of q
       for i=3 to N {
          f = p + q
          Print f
          q = p
          p = f
       }

Now, finally, let's write this up as a Java program:

In-Class Exercise 15: Trace the changing values of q, p, and f in the above program using a table.

Next, we'll explore a fascinating and very useful sequence:

Consider the sequence
X_n+1 = aX_n mod m
Here, a and m are integer constants.
The starting value of the sequence (called the seed) is X₁

In-Class Exercise 16: Suppose a=7, m=13 and X₁=1. Compute the first few values, up through X₄.

Next, let's write a program to print some of these values.

We'll begin with pseudocode:

       a = 7                // These are the two constants: a, m.
       m = 13               
       x = 1                // Starting value x=1
       n = 25               // Print the first 25 values

       for i=2 to n {
           x = (a*x) mod m
           Print x
       }

In-Class Exercise 17: Write a Java program called StrangeSequence that implements the above idea. The observe the output. What do you notice? Change a=5 and compare the output.

The above type of sequence is the basis for many random number generators.
In practical generators, m is usually very large, e.g., m = 2³¹ - 1
And a needs to satisfy the property that is satisfied by a=7 above (which a=5 does not satisfy. Can you guess what this property is?

The third math idea we'll explore: a program to explore a famous mathematical proof

This is a well-known formula:

     1 + 2 + ... + n   =   n(n+1)/2

There is a rather simple proof of this, attributed to the mathematician Carl Gauss.
What's interesting: Gauss was reportedly 10 years old when he discovered this proof.
The main idea:
- First, write the numbers 1 to n:
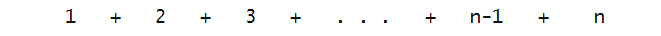
- Then, reverse the order and line up the reversed order underneath:
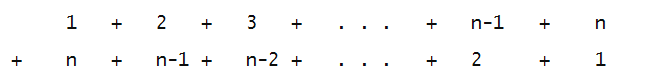
- Then, add:
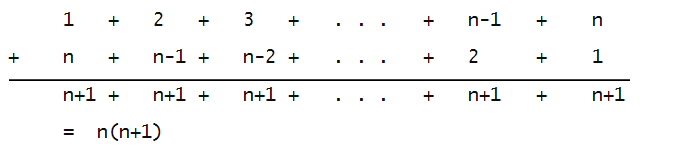
- Since the original sum is double-counted here, it must be true that
```
     1 + 2 + ... + n   =   n(n+1)/2
    
```

Now, let's explore this in a program:

public class Gauss {

    public static void main (String[] argv)
    {
	int n = 10;
	int s = 0;                  // Use this to accumulate the sum.
	int d = 0;                  // Use this to accumulate the double-sum.
	for (int i=1; i<=n; i++) {
	    int a = i;              // The number above.
	    int b = n-i+1;          // The number below.
	    s = s + i;              // Accumulate the sum.
	    d = d + (a + b);        // Accumulate the two terms: (n+1)
	}
	System.out.println (s);     // Print the sum.
	System.out.println (d);     // Print the double-sum.
	int f = n*(n+1)/2;
	System.out.println (f);     // To verify, print the formula.
    }

}

A problem with variables and nested for-loops

We'll solve the following problem: for any given n, compute
1 + 2¹ + 2² + 2³ + ... + 2ⁿ

That is, the sum of consecutive powers of 2.

As a first step, let's see if we can use a loop to compute a single power of 2:

Suppose we wish to compute 2^k for some k.
We know that
2^k = 2*2*2 ... *2 (k times)
Thus, what we could is:
       Start with p = 1
       Multiply by 2: p = p * 2
       Multiple that result by 2: p = p * 2
       ... etc

In pseudocode:

       p = 1  
       for i=1 to k {
          p = p * 2
       }

Let's put this into code and test:

In-Class Exercise 18: Trace the changing values of p in the above program using a table. Then, edit, compile and execute.

Next, let's look at pseudocode for the sum of powers:

       s = 1    
       for k=1 to n {
          Compute k-th power of 2
          Accumulate in s
       }
       Print s

Now, let's put this all together:

In-Class Exercise 19: Make a table with columns labeled k, i, p and s and trace the program, filling in the table step-by-step.

In-Class Exercise 20: Try a few other values of n, e.g., n=3 or n=4. Can you guess the mathematical formula for 1 + 2¹ + 2² + 2³ + ... + 2ⁿ?

Choosing variable names

Thus far, for simplicity, we have used short one-letter names for variables.

It is common to use longer, more meaningful names.

With this in mind, let's demonstrate more appropriate names by re-writing some earlier programs.

For example, the sum program:

Similarly, here's the Fibonacci program with more readable variable names.

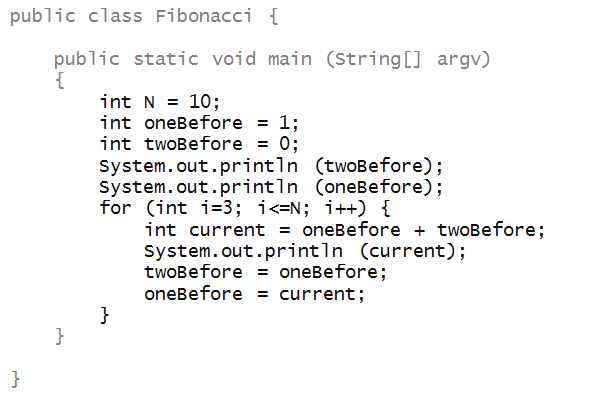
About variable names:

They are a matter of taste.
For programs with obvious mathematical connotation, it's probably best not to use long names.
Generally, loop-variable names tend to be short.

Shortcut operators

Recall the integer-sum program:

Here, the line


      sum = sum + i;

can be replaced with


      sum += i;

The += operator combines assignment and addition.

This can be applied to the other operators as well:


       s -= i;         // Same as s = s - i;
       p *= 2;         // Same as p = p * 2;
       d /= 2;         // Same as d = d / 2;

In-Class Exercise 21: Rewrite the SumOfPowersOf2 program using shortcut operators for multiplication and addition.

When things go wrong

As you might imagine, there are many ways to inadvertently create errors.

Let's start with compilers errors.

In-Class Exercise 22: Try to identify the compiler error (or errors), by reading each program below.
Program 1:

Program 2:

Program 3:

Program 4:

Next, let's look at some logical errors.

In-Class Exercise 23: Consider the sequence of numbers:
1, 2, 6, 42, 1806, 3263442, ....
Here, the n-th term is defined as
X_n = (X_n-1)² + X_n-1.
Thus, each term is the square of the previous term plus itself. Here is a program to compute the n-th term:

The program compiles, but has a mistake - can you find it?

In-Class Exercise 24: What is the error in the program below?

Sometimes an error is not entirely the programmer's fault but a lack of awareness of language limitations.

For example, consider the power-of-2 program from earlier:

In-Class Exercise 25: Edit, compile and test the above program. Now set n=40. What do you observe? What is the largest possible value of n for which you get a correct result?