Module 14: Science & Engineering Applications III - Cryptography and Computational Biology

Objectives

By the end of this module, you will be able to:

Demonstrate the use of shifts in a char array to implement a cipher.
Demonstrate the use of transposition in an array.
Demonstrate an application string equality testing in protein sequences.
Demonstrate substring search and its use in protein sequences.
Demonstrate substring extraction.
Compute molecular weight from protein sequence.
Demonstrate approximate matching and string distance.

The Caesar cipher

The essence of cryptography:

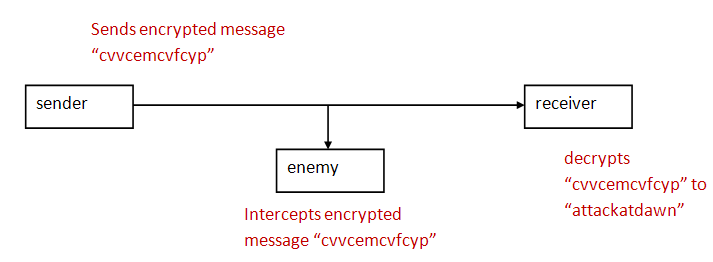
Although there is lots of two-way communication, in essence, it boils down to a Sender that needs to send a message to a Receiver in the presence of an enemy interceptor.
Goals:
- It should be hard for the enemy to decrypt.
- It should easy for sender to encrypt, and for the receiver to decrypt.
A cipher is an encryption technique.
The original text or message to be encrypted is called the plaintext.
The encrypted message or text is called: ciphertext.

One of the oldest ciphers is the Caesar cipher:

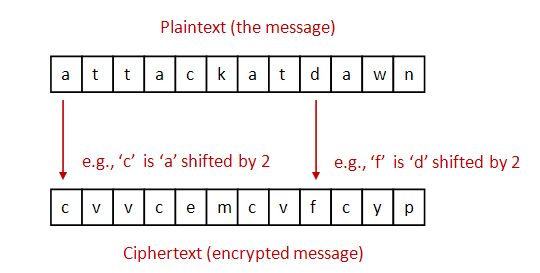
To simplify, let's assume: lowercase letters only (no whitespace or punctuation).
For encryption: each letter is shifted by a fixed amount (e.g., 2).
For decryption: shift back by the same amount.
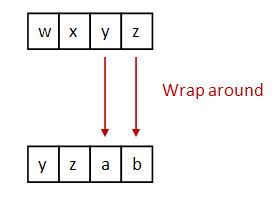
Important: use wraparound.

In-Class Exercise 1: Follow instructions in class to encrypt and decrypt a message.

In-Class Exercise 2: Consider only lowercase letters 'a' through 'z' and suppose 'a' is represented by 0, 'b' is represented by 1 ... etc. Next, suppose we do a Caesar shift by the amount s. Write an expression for computing the shifted character. Show how it works for 'z'.

Next, let's write some code to implement the Caesar cipher:

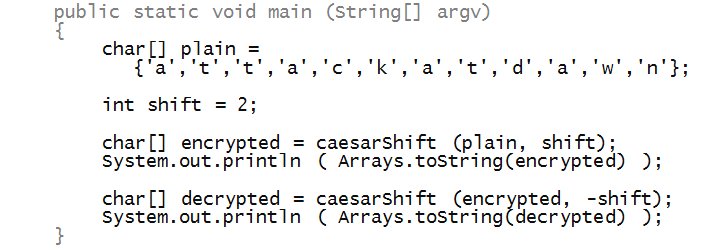
To begin, let's write the test code in main:
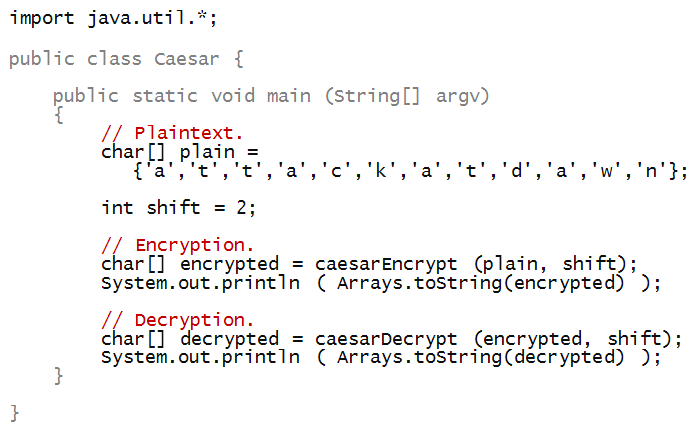
Notice that the method caesarEncrypt takes a char[] array (the plaintext), and shift as parameters:
And returns a char[] array:
To print the array after encryption, we have used a method called Arrays.toString from the Java library:
To be able to use some library methods, we need to import the library:
import statements need to appear at the top, outside the class:
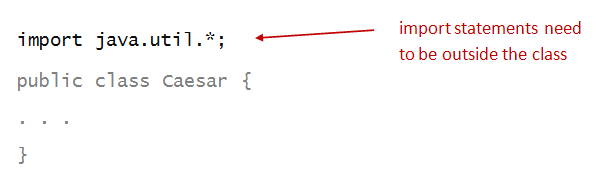
An import statement uses the import reserved word:
And names the library, in this case java.util:
The asterisk simply asks to import everything in the java.util library.
Alternatively, we could have imported just the class we need:

Now, let's write the code inside the method caesarEncrypt:

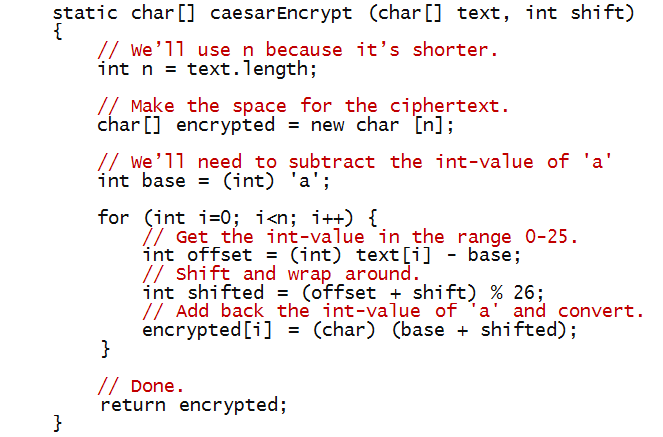
In-Class Exercise 3: Trace through the above method if it's called with with the letters "abc" and a shift of 2.

In-Class Exercise 4: Suppose k is an integer. What is the relationship between k % 26> and (k+26) % 26?

In-Class Exercise 5: Write the method caesarDecrypt so that the whole program works correctly.

In-Class Exercise 6: Follow instructions in class for this exercise.

Now, let's look at an alternative way of writing the same program:

It seems that we should be able to use the almost-symmetry between encryption in the following way:
Thus, decryption is merely a negative shift (shift in the reverse direction):
To do this, we'll use the property of the mod operator that we explored earlier:
We've added 26 so that the number being mod'ed is positive.

In-Class Exercise 7: Fill in the remaining code (in method caesarShift) to make the program work.

The Vigenere cipher

Improving on the Caeser cipher:

As we've seen, the Caesar cipher is rather easy to break.
The problem is: there are only 26 possible shifts
=> the same shift is used for each plaintext letter.
It's convenient of course: the receiver only needs to know the shift once
=> It can be used for many messages.
An idea for strengthening the encryption: use a different shift for each char in the text
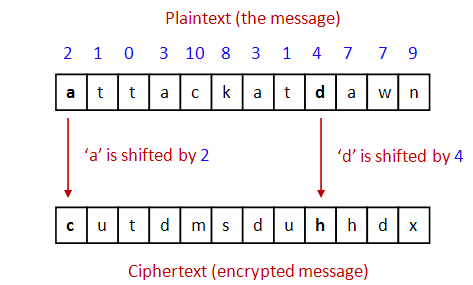
Unfortunately, there are several downsides:
- Both sender and receiver have to have communicated the sequence of "shifts" earlier.
  In this case, for example, both would have to "know"
```
  2 - 1 - 0 - 3 - 10 - 8 - 3 - 1 - 4 - 7 - 7 - 9  
          
```
- Because it's hard to remember, it would have to be stored somewhere, risking discovery.
- Messages can't be longer than the shift-pattern.

The Vigenere cipher addresses this problem:

First, note that shifts are numbers between 0 and 25.
=> A shift can be encoded as a letter!
Thus, a "shift of 3" can be expressed as a "shift by 'd'".

But is a pattern like


  c  b  a  d  k  i  d  b  e  h  h  j

any easier to remember than


  2 - 1 - 0 - 3 - 10 - 8 - 3 - 1 - 4 - 7 - 7 - 9?

Also, it is just as susceptible to discovery if written somewhere.
The "key" insight of Monsieur Vigenere:
- Both sender and receiver agree on a reasonable-size, easy-to-memorize key
  => A string of letters.
- Example: "bad cafe".
Then, the key is repeated (concatenated with itself) as much as needed to match the length of the text.
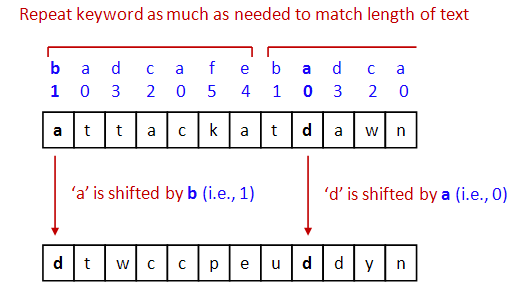
Then, above each text letter is a key letter.
=> They key letter specifies the shift.

In-Class Exercise 8: What is the 3-letter Vigenere key such that encryption with this key will result in the equivalent ciphertext that you get with a Caesar shift by 2?

Next, we'll work towards an implementation:

Let's start with the "test" code in main
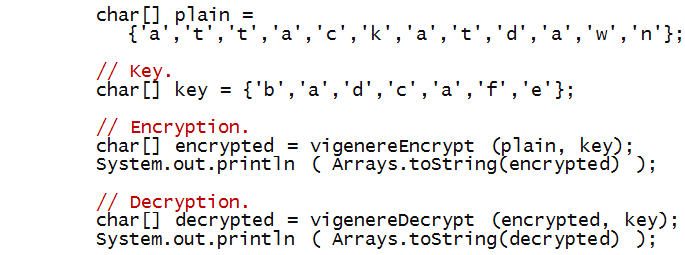
Next, consider vigenereEncrypt:
Notice we have used the same shiftChar method used with the Caesar cipher.
Decryption is symmetric, with the same key:
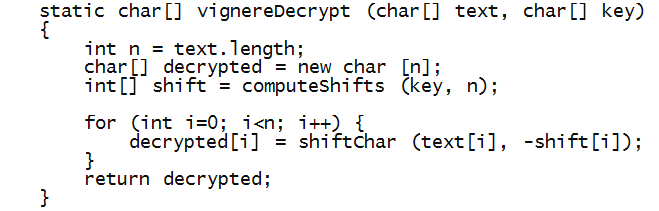
What's left: extending the key by repetition and returning the corresponding array of shifts.

In-Class Exercise 9: Write the code for computeShifts and complete the whole program so that both encryption and decryption work.

In-Class Exercise 10: Consider the following cipher:

First, find a random scramble of letters 'a' through 'z', e.g.

    m g y d v k a c n r o b p z s u f t q i e l w j x

Then, line up the regular alphabet above:

    a b c d e f g h i j k l m n o p q r s t u v w x y z
    m g y d v k a c n r o b p z s u f t q i e l x j w h

This is the letter substitution table: every time you see an 'a', replace it with an 'm'. Similarly, all b's are replaced by g's etc.

Now, for a given plain text message, do a letter-by-letter substitution given the above, e.g.

    a t t a c k a t d a w n
    m i i m y o m i d m x z

Then, miimyomidmxz is the ciphertext.

Clearly, decryption works by reversing the substitution. How does this cipher compare with the Caesar and Vigenere ciphers? Which would you rate as the best and why? The worst and why?

Transposition ciphers

The ciphers we've seen so far use letter substitutions: they are called substitution ciphers.

In a transposition cipher, all the original plaintext letters are used, but they are shuffled.

For example, one could reverse the characters:

     nwadtakcatta

Clearly, this is not as effective as other possible shuffles.

Let's consider a two-interleaving:

Here all the letters are array indices 0, 2, 4, ... are clustered together on the left in the order in which they occur, while the odd ones are to the right.
Once again, let's start with the test code in main:
Now let's write encryption, assuming an even-sized array:
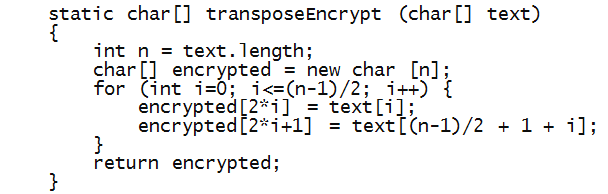
Notice the following:
- The for-loop only goes through only half the length.
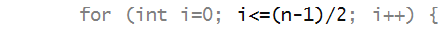
- The first half of the plaintext is copied in even-numbered locations:
- After which the right half of the plain text is copied into odd-numbered locations of the ciphertext:

In-Class Exercise 11: Write the code for decryption and complete the program.

In-Class Exercise 12: The above code does not work for odd-sized arrays. Try it with "attackatmidnight" and see what happens. Fix the code to handle odd-sized arrays.

Combining ciphers

One can easily encrypt already-encrypted text, e.g.

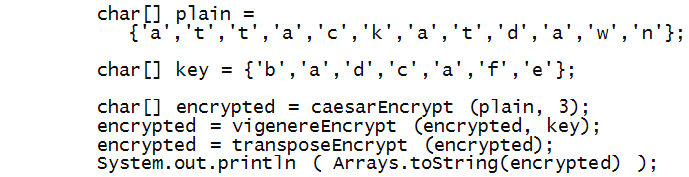
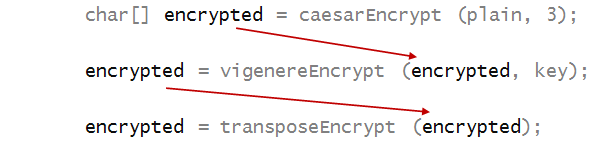
Notice how each successive encryption is fed as the plaintext to the next encryption:

In-Class Exercise 13: Pool together your code from the three ciphers and apply the above encryption. What is the resulting ciphertext. Then, show that the ciphertext decrypts when the decryption is applied in reverse order.

In-Class Exercise 14: With the same ciphers in the same order but using "java" as the Vigenere key, the following is the result of encryption: "miohgqwsfqoscdmrmdyvyuhpmffdfmgzmybb". Decrypt to find the original plaintext.

About cryptography:

Modern ciphers operate at the bit-level, not on characters, but the same principles apply.
Modern ciphers apply several types of encryption in sequence.
We have barely scratched the surface of cryptography.
"Crypto", as it's informally called by its practitioners, is vast subject with many deep and fascinating results.
Many key people involved in cryptography were or are computer scientists - such as Alan Turing.
Crypto is a part of a larger field called computer security, which also involves secure computing systems and networks.

Protein "strings"

Having scratched the surface of crypto, we'll now scratch another: computational biology.

What we'll do:

Understand that proteins (an important type of bio molecule) can be represented using strings.
=> the strings are called protein sequences.
Perform some types of operations on these protein sequences that are useful in biology.

Let's start by understanding what a protein is.

In-Class Exercise 15:

Look up proteins - what is a protein and what does it do?

Look up insulin. What is its purpose? What diseases are associated with insulin? What Nobel prizes were associated with insulin?

What we need to know about proteins:

Although a protein has a 3D shape, it can be considered a long chain of "units".
=> The 3D shape results from this chain folding on itself.
Each unit in the chain is determined by a particular kind of small (or sub-) molecule called an amino-acid.
There are 20 types of amino acids.

These are the 20:

# Amino Acid Symbol

1 Alanine A

2 Arginine R

3 Asparagine N

4 Aspartic acid D

5 Cysteine C

6 Glutamic acid E

7 Glutamine Q

8 Glycine G

9 Histidine H

10 Isoleucine I

11 Leucine L

12 Lysine K

13 Methionine M

14 Phenylalanine F

15 Proline P

16 Serine S

17 Threonine T

18 Tryptophan W

19 Tyrosine Y

20 Valine V

Think of the 20 amino acids as represented by their (20) letters:
```
      A R N D C E Q G H I L K M F P S T W Y V
    
```
Then, a protein is a "word" made from letters in this 20-letter alphabet.
For example: here is part of the insulin protein:
```
	F V N Q H L C G S H L V E A L Y L V C G E R G F F Y T P K T 
    
```
- It's length is 30.
- It happens to be called the B-chain in human insulin.

In-Class Exercise 16: As a puzzle just for fun, can you make a 5-letter English word out of the protein alphabet? A 6-letter one?

To start with, let's understand a couple of things about insulin:

Insulin is made from a precursor molecule call preproinsulin.
Preproinsulin is made directly from the gene for insulin.

For example, here is the 110-letter sequence for preproinsulin:

MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN

Parts of this are called the A-chain, B-chain, and C-chain respectively.

For example, this is the 30-letter B-chain above:

MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN

And the 21-letter A-chain:

MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN

The sequence in between is called the C-chain:

MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN

The real insulin molecule is actually a protein complex that is formed from the A and B chains.

Let's now work on some string problems related to insulin.

Before doing so, it'll help to review some methods available for strings in Java.

In-Class Exercise 17: Look up the following methods in the Java library under String: charAt, indexOf, length, substring, equals. Write down the first line of the method definition. That is, what are the parameters and return value for each?

To start with, let's look for the three chains in preproinsulin:

Suppose we are given:
1. The sequence for preproinsulin.
2. The A-chain and B-chain.
The goal: find where in the preproinsulin they occur, and extract the C-chain.

Here is the program:

	String preproSeq = "MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN";
	String aChain = "GIVEQCCTSICSLYQLENYCN";
	String bChain = "FVNQHLCGSHLVEALYLVCGERGFFYTPKT";

	// Find where the A and B chains occur in preproinsulin.
	int aIndex = preproSeq.indexOf (aChain);
	int bIndex = preproSeq.indexOf (bChain);
	System.out.println ("A chain starts at position " + aIndex);
	System.out.println ("B chain starts at position " + bIndex);

	// Extract the C-chain.
	int cIndex = bIndex + bChain.length();
	String cChain = preproSeq.substring (cIndex, aIndex);
	System.out.println ("C-chain: " + cChain);

In-Class Exercise 18: The following are the preproinsulin sequences for gorilla and owl monkey. Use the equals method to see whether they are the same as human preproinsulin. That is, write a short program to do this testing in main.

MALWMRLLPLLALLALWGPDPAAAFVNQHLCGSHLVEALYLVCGERGFFYTPKTRREAEDLQVGQVELGGGPGAGSLQPLALEGSLQKRGIVEQCCTSICSLYQLENYCN

MALWMHLLPLLALLALWGPEPAPAFVNQHLCGPHLVEALYLVCGERGFFYAPKTRREAEDLQVGQVELGGGSITGSLPPLEGPMQKRGVVDQCCTSICSLYQLQNYCN

Next, let's consider the problem of approximate string matching:

Suppose we don't know the identity of the A and B chains of the owl monkey.
We do know the human ones.
Thus, we'll solve this problem:
- We're given the preproinsulin sequence of the owl monkey:
```
MALWMHLLPLLALLALWGPEPAPAFVNQHLCGPHLVEALYLVCGERGFFYAPKTRREAEDLQVGQVELGGGSITGSLPPLEGPMQKRGVVDQCCTSICSLYQLQNYCN
```
- We know the human B-chain:
```
FVNQHLCGSHLVEALYLVCGERGFFYTPKT
```
- We want to know: which substring of the owl-monkey matches the human B-chain most closely.
To do this, we will develop the idea of distance between two strings.

In-Class Exercise 19: Propose an idea for quantifying the distance between words. For example, what would be the distance between "bold" and "bald"? What about "bold" and "boy"?

Consider the following computation of string distance:

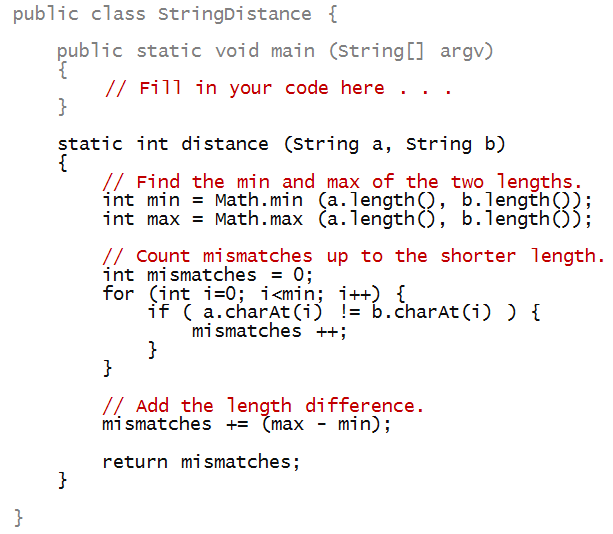
In-Class Exercise 19: Write code in main above to apply this distance measure to compare "bold" with each of the following strings: "bald", "boy", "old".

About string distance:

In general, there are many definitions of string distance.
The simple definition above failed for a simple "shifted" string.
In fact, in computational biology, there are some fairly complicated definitions that make use of statistics.

We'll use our simple distance measure to find the best B-chain match within the owl monkey chain.

For example, suppose we compare the human B-chain at the 5-th position of the owl-monkey preproinsulin:

MALWMHLLPLLALLALWGPEPAPAFVNQHLCGPHLVEALYLVCGERGFFYAPKTRREAEDLQVGQVELGGGSITGSLPPLEGPMQKRGVVDQCCTSICSLYQLQNYCN
     FVNQHLCGSHLVEALYLVCGERGFFYTPKT

To use the distance method we wrote earlier, we'd have to extract the sub-string from the preproinsulin sequence.

Here's a program that makes the comparison at the 5-th position.

	String owlMonkeyPrepro = "MALWMHLLPLLALLALWGPEPAPAFVNQHLCGPHLVEALYLVCGERGFFYAPKTRREAEDLQVGQVELGGGSITGSLPPLEGPMQKRGVVDQCCTSICSLYQLQNYCN";
	String humanB = "FVNQHLCGSHLVEALYLVCGERGFFYTPKT";

	int i = 5;
	String sub = owlMonkeyPrepro.substring (i, i + humanB.length());
	int d = distance (sub, humanB);
	System.out.println ("Distance=" + d + " at position=" + i);
	System.out.println ("Human B  : " + humanB);
	System.out.println ("Owl match: " + sub);

In-Class Exercise 20: Expand on the above code to search all possible positions in the owl-monkey preproinsulin and find the best possible match (with the least distance). Print the position where this occurs, and the distance.

In-Class Exercise 21: Now try the same thing with a few non-primates. Before running your code, which of the three do you expect to produce a result closest to human? Farthest?

Hummingbird:
IQSLPLLALLALSGPGTSHAAVNQHLCGSHLVEALYLVCGERGFFYSPKARRDAEHPLVNGPLHGEVGDLPFQQEEFEKVKRGIVEQCCHNTCSLYQLENYCN

Zebrafish:
MAVWLQAGALLVLLVVSSVSTNPGTPQHLCGSHLVDALYLVCGPTGFFYNPKRDVEPLLGFLPPKSAQETEVADFAFKDHAELIRKRGIVEQCCHKPCSIFELQNYCN

Fruitfly:
SSSSSSKAMMFRSVIPVLLFLIPLLLSAQAANSLRACGPALMDMLRVACPNGFNSMFAKRGTLGLFDYEDHLADLDSSESHHMNSLSSIRRDFRGVVDSCCRKSCSFSTLRAYCDS

Even when a mismatch looks very difficult, it is possible to identify reasonable matches.
=> This is the subject of advanced techniques in computational biology.

#	Amino Acid	Symbol
1	Alanine	A
2	Arginine	R
3	Asparagine	N
4	Aspartic acid	D
5	Cysteine	C
6	Glutamic acid	E
7	Glutamine	Q
8	Glycine	G
9	Histidine	H
10	Isoleucine	I
11	Leucine	L
12	Lysine	K
13	Methionine	M
14	Phenylalanine	F
15	Proline	P
16	Serine	S
17	Threonine	T
18	Tryptophan	W
19	Tyrosine	Y
20	Valine	V