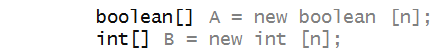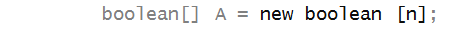Module 10: Conditionals

Objectives

By the end of this module, for simple programs with real numbers, you will be able to:

Evaluate Boolean expressions.
Construct Boolean expressions from English descriptions.
Mentally execute code with if, if-else, and if-multi-else statements.
Write and debug code with conditionals.
Write and debug code with conditionals inside loops.
Declare and use Boolean variables.
Identify new syntactic elements related to the above.

A simple example

Consider this program:

In-Class Exercise 1: Add an additional println right below the "Hey, ..." println. Compile and execute the program. Then, change the value of y to 6 and compile/execute. What is the output?

About the if-statement:

The if-statement above consists of several parts:
- The reserved word if:
- The condition (x>y)
- The block of code associated with the if:
Execution:
- The condition (x>y) is evaluated.
- If it turns out to be true at the moment of execution, the statements inside the if-block are executed.
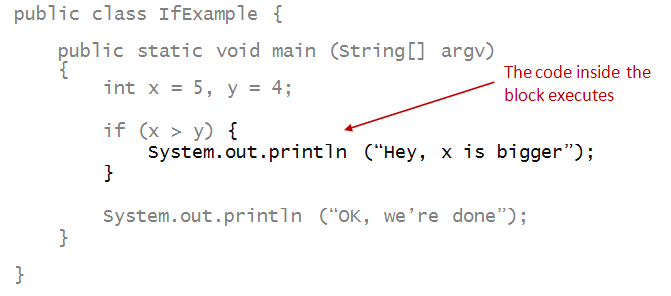
- Then, execution continues after the block:
If such a condition is not true, execution jumps to just after the if-block.

If-else

Consider this program:

If the if-condition (x>y) evaluates to true, the if-block executes:
Otherwise, the else block executes:

We can combine an else clause with an added if-clause:

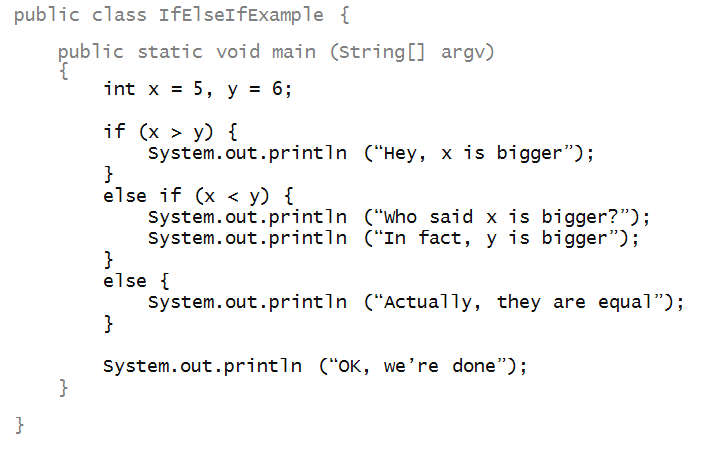
If the if condition is true, only the if-block executes:
If not, the else-if condition is evaluated:
If that's true, the appropriate block is executed:
If the second if-condition is false, the last else-clause executes:

Comparison operators:

These are Java's comparison operators:

       (x < y)                // Strictly less than.
       (x <= y)               // Less than or equal to.
       (x > y)                // Strictly greater than.
       (x >= y)               // Greater than or equal to.
       (x == y)               // Equal to.
       (x != y)               // Not equal to.

Thus, in the above example, we could have written:

In-Class Exercise 2: Are there any circumstances under which the last block executes?

Here, logic dictates that only some blocks can possibly execute.
Thus, sometimes it is not necessary to write some blocks of code if they'll never execute.

In-Class Exercise 3: Suppose we want to identify whether x has the largest value among x, y and z. Why doesn't the following program work?

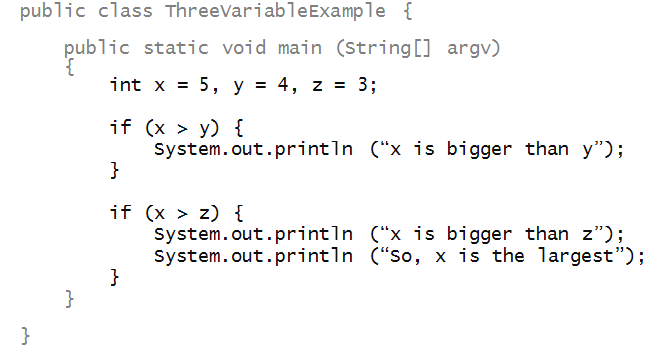
Can you alter the program to make it work?

Nested conditionals

Consider this program:

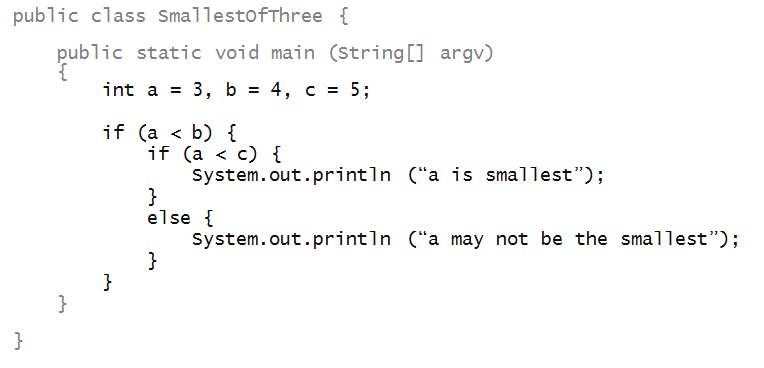
First, the outer if condition is evaluated:
Since that's true here, we get inside the if block:
The next thing to be executed is the inner if condition:
Since that's true here, we get inside that if-statement's if-block:
Note how execution goes from there:

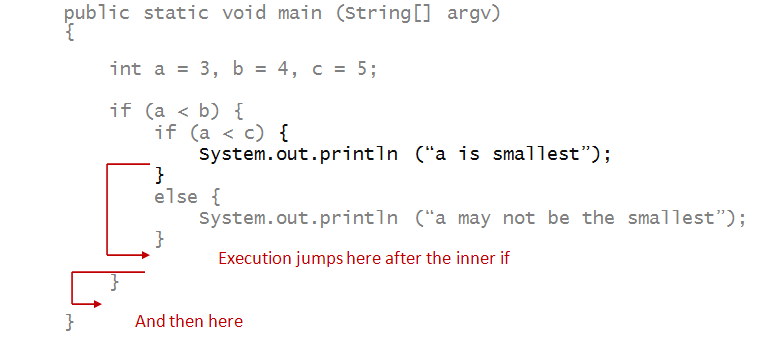
In-Class Exercise 4: Modify the above program so that it prints out, appropriately, one of "a is the smallest", "b is the smallest" or "c is the smallest", depending on the actual values of a, b and c. Try different values of these variables to make sure your program is working correctly.

Combining conditions

Consider this program:

The if condition combines two comparisons:
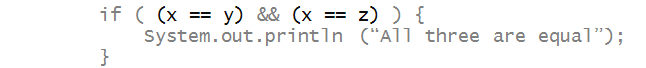
The combination uses the Boolean operator &&
- Read && as "AND".
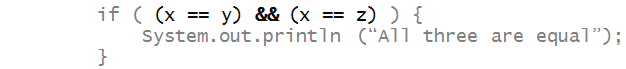
The "AND" operator works like this:
- The overall combination evaluates to true only when BOTH the individual conditions are true.

In-Class Exercise 5: Let's go back to this program:

Use a two-subclause if-statement to identify whether a is the smallest of the three.

In-Class Exercise 6: Now extend this idea to identify which of the three variables has the smallest value.

The OR operator:

Here, the || operator should be read as "OR".
If either subclause is true, the whole is true:

The NOT operator:

In-Class Exercise 7: Modify the above to determine whether all three variables have different values.

The NOT operator can be applied to a larger clause made of sub-clauses:

Here, the inner clauses are first evaluated, and the result is "flipped" to see if the NOT clause turns out to be true:

Conditionals and loops

We'll write a program to loop through a range of numbers, print the even ones:

In-Class Exercise 8: Trace through the above program as i changes in the for-loop. Then modify the program to print whether i is odd or even.

In the next example, we'll find the minimum of a function (approximately):

Consider the function f(x) = 20 + 100(x³ - x²) in the range [0,1].
Let's write a program to find its minimum value in the range:

In-Class Exercise 9: Add a println inside the loop to print the current value of f each time it's calculated.

In-Class Exercise 10: Print both the minimum as well as the x value where the minimum occurs.

In-Class Exercise 11: Use DrawTool.java to plot both the points of the function as well as the x value where the minimum occurs.

Conditionals and arrays

Consider this example:

In-Class Exercise 12: Trace through i and sum in the above example.

In-Class Exercise 13: Write a program using the same array as above that does the following: it searches the array for a given integer and prints out whether the search was successful. For example, suppose we want to search a given array to see if it has the element 4. Then, for the above array, the output should be "Yes, 4 exists in the array".

Minimum and maximum elements in an array:

This is often a useful thing: to find the range of some given data.
As we'll see, it is also something that will help in sorting data.
Here's a first attempt at finding the maximum:

In-Class Exercise 14: Trace the values of i and max through the above program. Can you think of an array that would cause the program to fail to find the maximum? How would you fix the problem?

Now, let's add the minimum:

In-Class Exercise 15: Again, find an array for which the above will not work and fix the problem.

In-Class Exercise 16: Suppose we had used an else-if as below.

Trace through the program to see if this works. Then, change the value of the first element of the array to -50 and trace again.

In-Class Exercise 17: Consider this version:

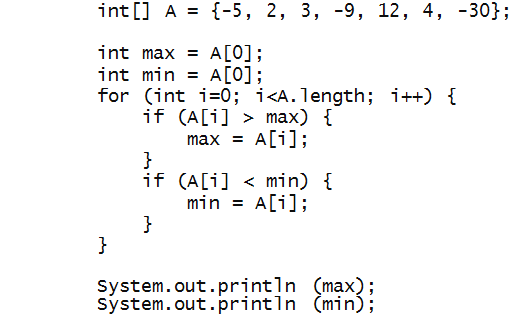
Trace through the program to see if this works. Would this work if we had initialized min and max to any element of the array, such as A[3]?

Working with more than one array

Let's write a simple program to copy one array (of numbers) into another, ensuring that if a number is negative, we copy its positive part:

Note: we created array B of the same length as A.
No additional condition was needed in the else-clause.

Now, we'll do something a little harder: copy over only those elements that are positive:

In-Class Exercise 18: Trace through the above program to see how it works. Draw a picture showing the contents of array B at each step. Then, modify the program so that it prints only the elements copied over into B.

In-Class Exercise 19: Add code to the template below so that you copy over into B only those numbers from A that are multiples of 3 or 4. Then print out these resulting numbers from array B.

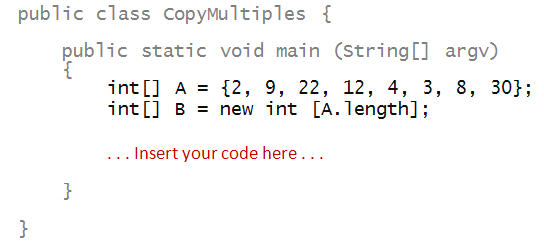
Thus, you should print out: 9, 12, 4, 3, 8, 30.

Nested for-loops

Now we'll look at a few examples of working with arrays and conditionals in nested loops.

First, let's examine an array to see if it has duplicates:

In-Class Exercise 20: Trace through the above program, drawing a picture of the array and tracking i and j.

Note:

First, notice the starting value for j:
Next, notice that the two loop entry conditions are different:
This is a "standard" form of nested-loop that allows all possible pairs of elements to be compared.

Next, we'll write a program to simply count occurences of each integer in an array:

In-Class Exercise 21: Trace through the above program, drawing a picture of the occurenceCount array and tracking its values.

Notice how we used an array value as an index:
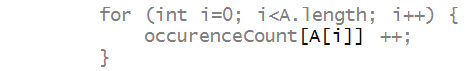
The output above resulted in printing the occurence count multiple times for some integers.

Here's one way to address the problem:


    public static void main (String[] argv)
    {
        int[] A = {2, 9, 2, 6, 4, 3, 3, 2};
        int max = 9;
        int[] occurenceCount = new int [max+1];
        for (int i=0; i<A.length; i++) {
            occurenceCount[A[i]] ++;
        }
        for (int k=0; k<occurenceCount.length; k++) {
            if (occurenceCount[k] > 0) {
                System.out.println (k + " occurs " + occurenceCount[k] + " times");
            }
        }
    }

In-Class Exercise 22: Execute the above program to see how it works. Then, trace through the second for-loop above.

Rearranging an array

We'll start with a simple task: find the smallest value in an array and move it to the first location in the array.

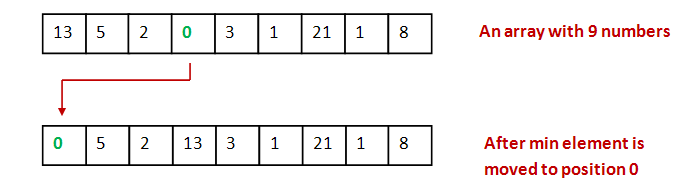
The program:

In-Class Exercise 23: Execute the above program. Then, trace through the first for-loop above. What would happen we started with i=0 in that for-loop?

In-Class Exercise 24: Add code to the above program so that, after the min element is moved to position 0, the next smallest element (one of the 1's above) is moved into position 1.

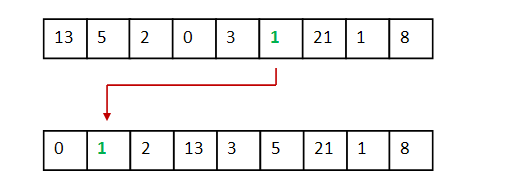
Change the data in the array several times to see if your program works.

We'll now generalize this idea to move the k-th smallest element to the k-th position:

	int[] A = {13, 5, 2, 0, 1, 3, 21, 1, 8};
	
	for (int k=0; k<A.length-1; k++) {
	    
	    // Default assumption: k-th element is k-th min.
	    int min = A[k];
	    int minPosition = k;

	    // Now find the min amongst elements from
            // positions k onwards.
	    for (int i=k+1; i<A.length; i++) {
		if (A[i] < min) {
		    min = A[i];
		    minPosition = i;
		}
	    }

	    // Swap min into position k.
	    int temp = A[k];
	    A[k] = A[minPosition];
	    A[minPosition] = temp;
	}

	// Print.
	for (int i=0; i<A.length; i++) {
	    System.out.println (A[i]);
	}

In-Class Exercise 25: Trace the values of these variables: k, i, min and minPosition. Then, execute the above program to see the result. What is the result? What have we achieved?

In-Class Exercise 26: Is the variable min really needed? Re-write the program to do without it (but using the other variables).

In-Class Exercise 27: Write a variation of the above program so that the maximum element is swapped into the first place (position 0), then the next largest is swapped in the second place (position 1) ... etc.

Boolean variables

What is a Boolean variable?

An int variable takes integer values like: 12, 256, or -9.
A double variable takes on values like 3.141, -14.0, or 2.718.
A boolean variables takes on one of only two values: true or false.

An example:

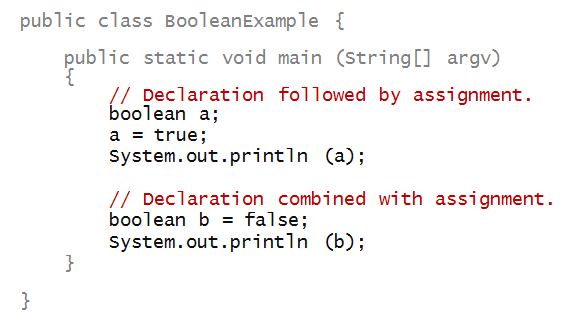
boolean, true and false are reserved words.
Note: true and false are not in quotes.

Boolean operators:

Two binary operators: && and ||
One unary operators: !
An example:

To understand the && operator:

Let's see what c could be based on all possible combinations of a and b values:

a b c = a && b

false false false

false true false

true true true

true false false

In short, the result of an AND operation is true only when both operands are true.

Similarly, let's look at the || operator:

Let's see what c could be based on all possible combinations of a and b values:

a b c = a || b

false false false

false true true

true true true

true false true

In short, the result of an OR operation is false only when both operands are false.
The ! operator:

a !a

true false

false true
In short, the NOT operator flips the value.
Note: the above table describes some of the "rules" for logic.

Using Boolean variables

Let's now use Boolean variables in a few examples.

Suppose we wish to solve the following problem:

We are given an array of integers and an additional integer.
Our goal is to search the array to see if the additional integer is in the array.
We are to print "found" if it's there, else "not found" if it's not there.
Consider this program:

In-Class Exercise 28: Trace through the program. Explain why this does not accomplish the task.

Let's make another attempt:

In-Class Exercise 29: Explain why this does not accomplish the task either.

Instead, let's use a Boolean variable to flag whether we've found the item in the array.

In-Class Exercise 30: Trace through and convince yourself that this works. Try another searchvalue that isn't actually in the array. Will this work if found is initialized to true?

Note: one can replace if (found == true) with if (found):

Boolean arrays

Just as we created arrays of int's or double's, we can create boolean arrays.

For example:

Observe how similar the declaration is to an integer array:
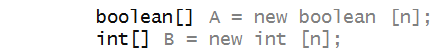
Again, space is created using the new reserved word:

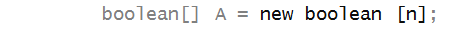
In-Class Exercise 31: Suppose we replaced the second for-loop with

Without typing up the program, identify what gets printed out.

Next, let's develop an application in steps: counting all the prime numbers less than or equal to some given n.

Let's start by eliminating all the numbers divisible by 2.

Of course, these are not the prime numbers (yet).
Eventually, we'll eliminate the numbers divisible by 3, then the numbers divisible by 4 etc.
Notice the general idea:
- We start by assuming all are prime.
- Then, we eliminate all that are divisible by 2.

In-Class Exercise 32: Why do we create an array of size n+1 above? Why do the second and third for-loops begin with 3?

In-Class Exercise 33: Modify the above code so that we eliminate both multiples of 2 and multiples of 3.

To identify the primes we need to eliminate all numbers that are divisible by some other number.

Thus, we will replace the second for-loop with this nested one:

Thus, we first eliminate all numbers divisible by k=2 (outermost loop).
Then, we eliminate all numbers divisible by k=3, etc.

In-Class Exercise 34: Implement the above program to count the primes, and confirm that it works.

In-Class Exercise 35: Trace through the above loop when n=15 by drawing picture of the array and its contents after each outerloop iteration.

In-Class Exercise 36: You should notice some unnecessary iterations through the outer for-loop. What is a more reasonable upper limit for the outer loop?

Reading and writing

First, reading:

When seeing
say to yourself:
- "Here's an if-block that may or may not execute."
- "What follows the if-block (the second println) always executes".
Read aloud the if-construct as: "if x > y then ... (the first println)".
Similarly when seeing a larger if-else, focus on the structure:
Say to yourself:
- "Only one of the three code blocks will execute."
- "The second condition is evaluated only if the first one is false."
- "We reach the third block only if both the previous two conditions fail."
When seeing a complex condition like
break it up into a hierarchical view:

In-Class Exercise 37: Draw a hierarchical picture that matches the conditional below.

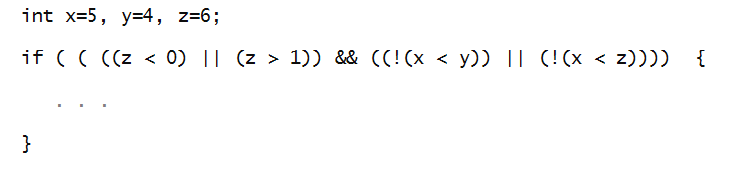
Then, evaluate it to see whether the result is true or false. Write down the true/false values at intermediate levels of the hierarchy.

Writing:

Remember to type in the matching right bracket immediately after typing in the left one.
Use spacing and layout consistent with the above example.

When things go wrong

In-Class Exercise 38: Identify the four errors in this piece of code:

In-Class Exercise 39: Fix the errors in the if condition to make this print "Success".

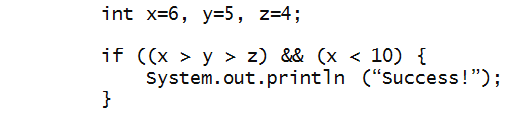
First, try to find the problems without compiling. Then, fix the code and see if you were right while reading.

In-Class Exercise 40: What does the following print out?

Fix the problem.

In-Class Exercise 41: The following code intends to print out alternate array elements starting from the end, but only if the elements aren't negative.

However, there are two problems. Can you see the problems just by reading? Fix the problems.

In-Class Exercise 42: The following code intends to search an array for a given searchValue to print true or false, depending on whether it was found or not.

Trace through the above program by hand to predict what it prints. Then, fix the problem.

a	b	c = a && b
false	false	false
false	true	false
true	true	true
true	false	false

a	b	c = a \|\| b
false	false	false
false	true	true
true	true	true
true	false	true