\( \newcommand{\eqb}[1]{\begin{eqnarray*}#1\end{eqnarray*}} \newcommand{\eqbn}[1]{\begin{eqnarray}#1\end{eqnarray}} \newcommand{\bb}[1]{\mathbf{#1}} \newcommand{\nchoose}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array}\right)} \newcommand{\defn}{\stackrel{\vartriangle}{=}} \newcommand{\eql}{\;\; = \;\;} \definecolor{dkblue}{RGB}{0,0,120} \definecolor{dkred}{RGB}{120,0,0} \definecolor{dkgreen}{RGB}{0,120,0} \newcommand{\bigsp}{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \newcommand{\plss}{\;\;+\;\;} \newcommand{\miss}{\;\;-\;\;} \newcommand{\implies}{\Rightarrow\;\;\;\;\;\;\;\;\;\;\;\;} \)

Module 5: Pattern Search

Module objectives

By the end of this module, you will be able to:

Demonstrate how to write pseudocode for solving the text search problem.
Demonstrate how to implement the Rabin-Karp text search algorithm.
Explain the principle behind the Knuth-Morris-Pratt and Boyer-Moore-Horspool algorithms for text search.
Show how a finite automaton can be used for text search.
Show how to construct an NDFA for regular expressions.
Explain how web documents are indexed for searching.

5.1 Problem Definition

Simple description:

Given two strings of characters, the "text" and the "pattern", find the first occurence of the "pattern" (as a substring) in the "text".
Terminology:
- Pattern: string or string-specification you are looking for.
- Text: sequence of characters in which you are searching.

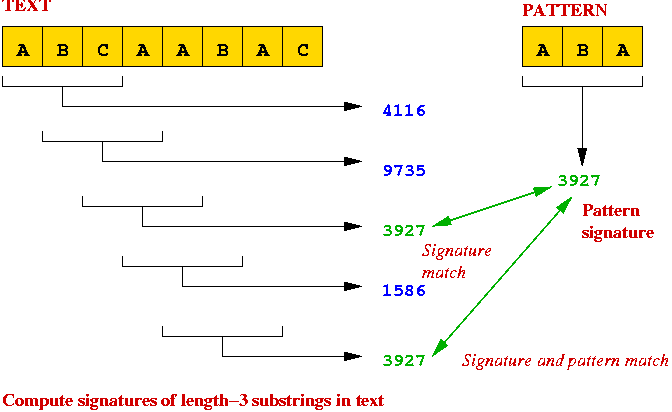
Example:

A pattern "BAC" that is found in the text "ABABACBABABA"


 A B A B A C B A B A B A
       B A C

Pattern "BAD" is not found in text "ABABACBABABA"

Practical issues:

Type of data:
- Usually: text (characters).
- Others: image data, bitstrings.
How is the data presented to the algorithm?
- Usually: two arrays of characters.
- Other ways: files, database tables.

Typical operations supported by the algorithm (Java):


public interface PatternSearchAlgorithm {

  public int findFirstOccurrence (char[] pattern, char[] text);

  public int[] findAllOccurrences (char[] pattern, char[] text);

}

Variations:
- Are multiple searches expected on the same text?
  ⇒ text can be pre-processed.
- Find all occurrences of pattern.
- Find largest-prefix of pattern in text (closest-match).
- Multiple patterns: wildcards, regular expressions.
  Example:
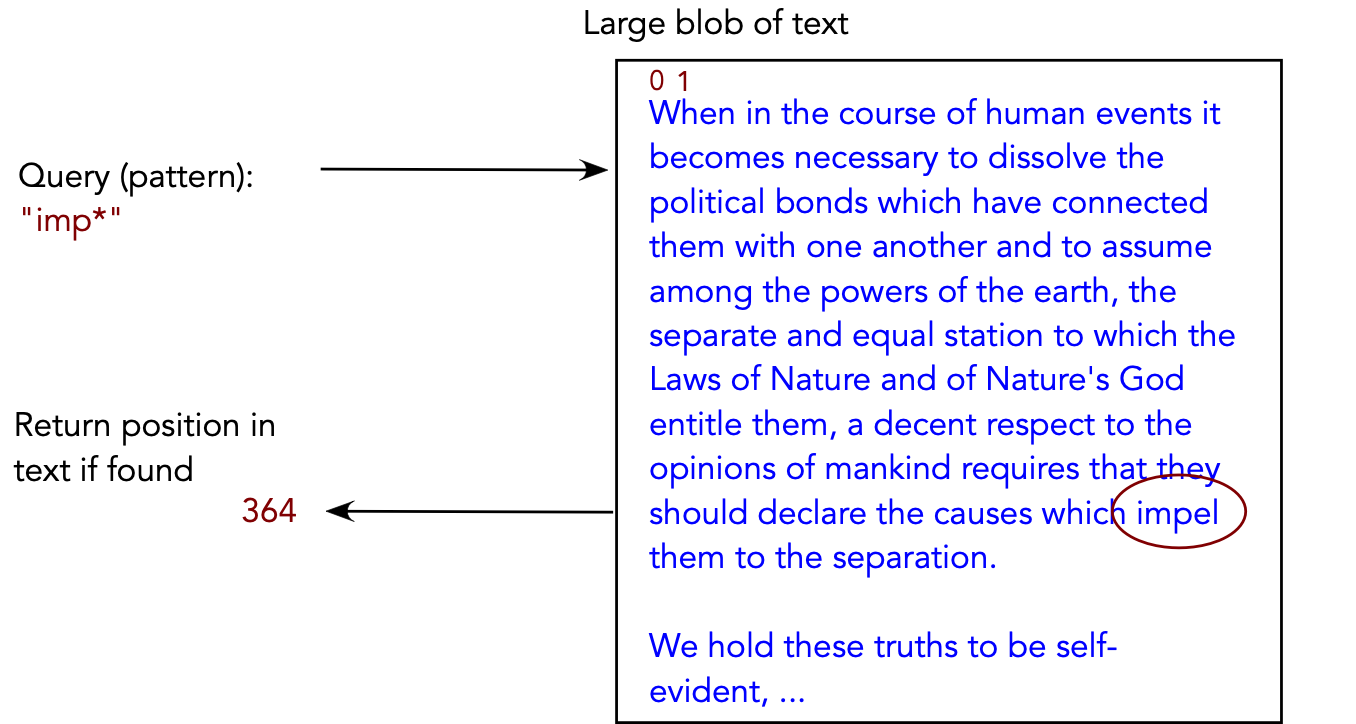
```
      grep in*face *.java 
      
```
  (Find all lines containing words that match the pattern "in*face" in all .java files).
- Multiple documents (texts).
Applications:
- Editors.
- Databases.
- Document searching.
- Pattern recognition (images, character recognition).

In-Class Exercise 5.1: Download this template and implement the straightforward iterative algorithm for finding a pattern within a text. Both the pattern and text are of type char[] (arrays of characters). You will also need UniformRandom.java.

Start by writing pseudocode for two versions: one with for-loops and one with while-loops.

Analyse the complexity of your algorithm for a pattern of size m and a text of length n.

Implement the algorithm in the template.

Write pseudocode for an alternative recursive version. What is its running time in terms of m and n?

5.2 Using Signatures: The Rabin-Karp Algorithm

Key ideas:

Compute the "signature" of the pattern.
Compute the "signature" of each substring of the text.
Scan text until signature matches
⇒ potential match, so perform string comparison.

Details:

Recall how a typical signature is computed:

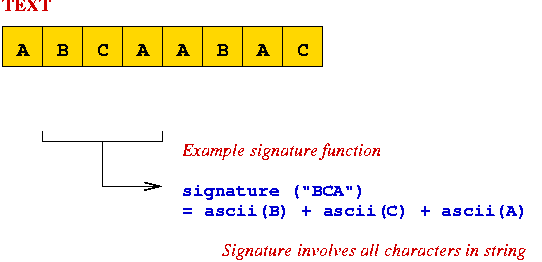
⇒ signature involves all characters
⇒ computing signature for each substring takes O(m) time.
⇒ no faster than naive search.
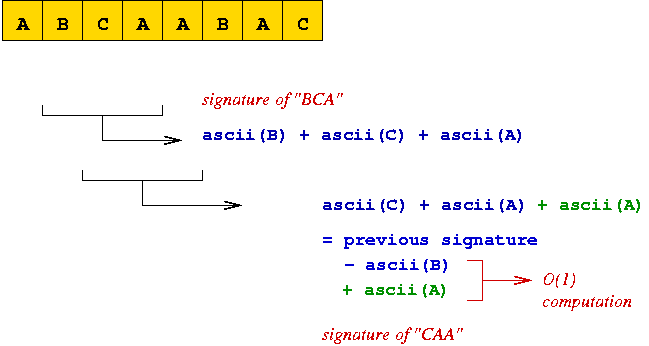
Observation: two successive substrings differ by only two characters.

⇒ next signature can be computed quickly (O(1)).
Note: simple addition of ascii values has been shown to be less effective.
⇒ use a different signature function.

Let's put this idea into pseudocode:


Algorithm: SignaturePatternSearch (pattern, text)
Input: pattern array of length m, text array of length n

1.   patternHash = computePatternSignature (pattern);
2.   texthash = compute signature of text[0]...text[m-1]
3.   lastPossiblePosition = n - m               // No match possible after this position: 
4.   textCursor = 0
5.   while textCursor <= lastPossiblePosition
6.     if textHash = patternHash                // Potential match. 
7.       if match (pattern, text, textCursor)
8.         return textCursor                    // Match found 
9.       endif
10.    endif
11.    textCursor = textCursor + 1
12.    textHash = compute signature of text[textCursor],...,text[textCursor+m-1]
13.  endwhile
14.  return -1
Output: position in text if pattern is found, -1 if not found.

Rabin and Karp used a different signature function to lower the chances of a false positive.
- Let m be the pattern length.
- Define the signature of the m-length substring starting at text[i] to be:
  
  f(text[i],...,text[i+m-1])
  = text[i] * d^m-1 + text[i+1] * d^m-2 + ... + text[i+m-1] * d⁰.
- Then, for the next substring:
  
  f(text[i+1],...,text[i+m])
  = text[i+1]*d^m-1 + text[i+2]*d^m-2 + ... + text[i+m]*d⁰.
  = d * (f(text[i],...,text[i+m-1]) - text[i]*d^m-1 + text[i+m]
- Suppose we use the short form: f_i = f(text[i],...,text[i+m-1])
  Then, f_i+1 = d * (f_i - text[i]*d^m-1) + text[i+m]
What is d?
- d can be any positive integer.
- Choose d so that d^k can be computed fast
  ⇒ d is a power of 2.
- Example: d=16 or d=32.
What if d^k gets too large?
⇒ Overflow can occur.
Use modulo arithmetic to avoid overflow:
- Let q be a large prime number.
- Choose q so that (d+1)*q is less than the largest integer.
  (In Java: largest integer is Integer.MAX_VALUE).
- Use this fact: if x mod q = y mod q and a mod q = b mod q, then:
  - (x+a) mod q = (y+b) mod q
  - (x*a) mod q = (y*b) mod q.
- Essentially, all arithmetic operations can be performed "mod q".
- Thus, to compute
  
  f_i+1 = d * (f_i - text[i]*d^m-1) + text[i+m]
  we can instead compute
  - t₁ = d^m-1 mod q
  - t₂ = (text[i]*t₁) mod q
  - t₃ = (d * (f_i - t₂) ) mod q
  - f_i+1 = (t₃ + text[i+m]) mod q
- The "mod q" approach guarantees that two equal strings will have the same signature.
What if two different substrings have the same signature?
- Identical signatures do NOT mean identical substrings.
- A string comparison is still needed if the signatures match.
  ⇒ will happen in only a few cases.

Pseudocode:


Algorithm: RabinKarpPatternSearch (pattern, text)
Input: pattern array of length m, text array of length n
     // Compute the signature of the pattern using modulo-arithmetic. 
1.   patternHash = computePatternSignature (pattern);
     // A small optimization: compute d^m-1 mod q just once. 
2.   multiplier = d^m-1 mod q;
     // Initialize the current text signature to first substring of length m. 
3.   texthash = compute signature of text[0]...text[m-1]
     // No match possible after this position: 
4.   lastPossiblePosition = n - m
     // Start scan. 
5.   textCursor = 0
6.   while textCursor <= lastPossiblePosition
7.     if textHash = patternHash
          // Potential match. 
8.       if match (pattern, text, textCursor)
           // Match found 
9.         return textCursor
10.      endif
         // Different strings with same signature, so continue search.        
11.    endif
12.    textCursor = textCursor + 1
       // Use O(1) computation to compute next signature: this uses 
       // the multiplier as well as d and q. 
13.    textHash = compute signature of text[textCursor],...,text[textCursor+m-1]
14.  endwhile
15.  return -1
Output: position in text if pattern is found, -1 if not found.

Example:


 A B A B A C B A C A C A B A          TextHash=2199650 patternHash=2231457
 B A C A

 A B A B A C B A C A C A B A          TextHash=2231425 patternHash=2231457
   B A C A

 A B A B A C B A C A C A B A          TextHash=2199651 patternHash=2231457
     B A C A

 A B A B A C B A C A C A B A          TextHash=2231458 patternHash=2231457
       B A C A

 A B A B A C B A C A C A B A          TextHash=2200705 patternHash=2231457
         B A C A

 A B A B A C B A C A C A B A          TextHash=2265187 patternHash=2231457
           B A C A

 A B A B A C B A C A C A B A          TextHash=2231457 patternHash=2231457
             B A C A

 A B A B A C B A C A C A B A          Pattern found
             B A C A

Analysis:

The pattern signature is computed once: O(m).
The first text signature takes O(m) time.
Each subsequent signature takes O(1) time
⇒ O(m+n) time overall.
However, in theory a "false" match could occur every time.
⇒ comparison required at every text position.
⇒ O(mn) time overall.
In practice, this is unlikely: O(m+n) time on the average.
Recall: the naive algorithm takes O(mn) time.
How different is O(mn) from O(m+n)?
if m = n/2 then mn = O(n²) but m+n = O(n).

In practice:

Signatures take time to compute
⇒ naive search often performs better.
Signature approach not worth it for small m (pattern length).
The signature technique is very general
⇒ can apply to 2D patterns, other kinds of data.

In-Class Exercise 5.2: Download this template and implement the Rabin-Karp algorithm but with a different signature function. Use the simple signature of adding up the ascii codes in the string (shown in the second figure in this section).

5.3 The Knuth-Morris-Pratt Algorithm

Key ideas:

The particular sequence of characters in the pattern can be exploited.
For example, consider
```
 B A B C A B A B A B A B B A C A A B          
           B A B A B B

 B A B C A B A B A B A B B A C A A B          
               B A B A B B
```
- In the first line, we know that five characters matched.
  ⇒ partial match.
- This means that the text contained "B A B A B".
- Thus, the "B A B" in the first part of the pattern could be matched against the second "B A B" in the text.
- We could pre-compute all such possibilities.
- This will allow "skipping" parts of the text.
Observations about skipping:
- In the above example, we can skip two places to the right.
- Note: we don't have to compare the "B A B"
  ⇒ Can start comparison later in the pattern
  ⇒ In the above example: start comparing at the "A" in "B A B A".
  ⇒ No backing up required!
- Thus, the text-cursor always moves right.
  ⇒ we only decide where in the pattern to start comparing.
  ⇒ need to pre-compute pattern-shifts in case of partial matches.
We will build a function called nextIndex that will take the mismatch position (in the pattern), and return the "next pattern position to start comparing".

Example:

Before going into detail, consider an example.
Text = "B A B C A B A B A B A B B A C A A B"
Pattern = "B A B A B B"
Suppose the nextIndex function turns out to be: (we'll learn how to compute it later)

Mismatch Position nextIndex

0 0

1 0

2 0

3 1 (Infer: match up to 0)

4 2 (Infer: match up to 1)

5 3 (Infer: match up to 2)

Let's apply this nextIndex function to the text:


 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 0
 B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 1
 B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 2
 B A B A B B

 B A B C A B A B A B A B B A C A A B          Mismatch at pattern position 3 nextIndex=1
 B A B A B B

 B A B C A B A B A B A B B A C A A B          Mismatch at pattern position 1 nextIndex=0
     B A B A B B

 B A B C A B A B A B A B B A C A A B          Mismatch at start of pattern: shifting right
       B A B A B B

 B A B C A B A B A B A B B A C A A B          Mismatch at start of pattern: shifting right
         B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 0
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 1
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 2
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 3
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 4
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Mismatch at pattern position 5 nextIndex=3
           B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 3
               B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 4
               B A B A B B

 B A B C A B A B A B A B B A C A A B          Matched up to pattern position 5
               B A B A B B

 B A B C A B A B A B A B B A C A A B          Pattern found
               B A B A B B

Computing the nextIndex function:

The hard part is understanding how to compute the nextIndex function.

At first, it may seem that having a high-degree of overlap is good:


 E A A A A E A A A A C A A A A
   A A A A F

 E A A A A E A A A A C A A A A
     A A A A F

Here, the overall "shift" was only one space.

Now consider:


 E A B C D E A A A A C A A A A
   A B C D F

 E A B C D E A A A A C A A A A
           A B C D F

In this case: the overall shift was "four spaces" (much better).

What made the difference?
- If the pattern has very little repetition in the pattern, the shift will be larger.
- If the pattern has a lot of repetition, the shift will generally be smaller.

In-Class Exercise 5.3: Consider this partial match:


 E A B C A B C A B A B C E A A A A C A A A A
   A B C A B C A F

How many letters can we skip? What about this case (below)?


 E A B C B B C A C A B C E A A A A C A A A A
   A B C B B C A F

What is the intuition? Consider this example:
```
 E A B A B E A A A A C A A A A
   A B A B F

 E A B A B E A A A A C A A A A
       A B A B F
```
The amount shifted depends on how large a "prefix of the pattern" is a "suffix of the matched-text".
Consider the first example again:
```
 E A A A A E A A A A C A A A A
   A A A A F
```
- The A A A prefix of the pattern is a suffix of the matched text A A A A
- That's why we must consider the possibility of matching it:
```
 E A A A A E A A A A C A A A A
     A A A A F
 
```
Second example:
```
 E A B A B E A A A A C A A A A
   A B A B F
```
- The A B prefix of the pattern is a suffix of the matched text A B A B.
Thus, intuitively, the amout to slide forward depends on the prefix-suffix match:
- The more the match, the less we can slide forward.

The relation with nextIndex:

Consider the first example:
```
 E A A A A E A A A A C A A A A          Mismatch at pattern position 4 nextIndex=3
  
```
- Here, we slide forward one space.
- But four characters were matched.
  ⇒ need to start comparisons at position 3 (fourth character) in pattern.
  ⇒ nextIndex = 3.
```
   A A A A F
 E A A A A E A A A A C A A A A
     A A A A F
  
```

Consider the second example:


 E A B A B E A A A A C A A A A          Mismatch at pattern position 4 nextIndex=2

In this example, we slide forward two spaces.

Since two characters match, the comparisons start at position 2.
⇒ nextIndex=2.


   A B A B F
 E A B A B E A A A A C A A A A
       A B A B F

How to define nextIndex:
- Notice: nextIndex is the length of the largest prefix of the pattern that is a suffix of the matched-text.
- Alternatively: the length of the largest suffix of the matched-text that is a prefix of the pattern.
- But: the matched text is also in the pattern!
  ⇒ can pre-compute nextIndex using only the pattern.
Formal definition:
- Suppose the mismatch occurs at the k-th character (in the pattern).
  ⇒ first k-1 characters of the pattern have matched.
- Call this k-1 substring the matched part.
- Let nextIndex = largest suffix of matched part that is also a prefix.

Pseudocode:


Algorithm: KnuthMorrisPrattPatternSearch (pattern, text)
Input: pattern array of length m, text array of length n
     // Compute the nextIndex function, stored in an array: 
1.   nextIndex = computeNextIndex (pattern)
     // Start the pattern search. 
2.   textCursor = 0
3.   patternCursor = 0
4.   while textCursor < n and patternCursor < m
5.     if text[textCursor] = pattern[patternCursor]
         // Advance cursors as long as characters match. 
6.       textCursor = textCursor + 1
7.       patternCursor = patternCursor + 1
8.     else
         // Mismatch. 
9.       if patternCursor = 0
           // If the mismatch occurred at first position, simply 
           // advance the pattern one space. 
10.        textCursor = textCursor + 1
11.      else
           // Otherwise, use the nextIndex function. The textCursor 
           // already points to the next place to compare in the text. 
12.        patternCursor = nextIndex[patternCursor]
13.      endif
14.    endif
15.  endwhile
16.  if patternCursor = m
       // If there was a match, return the first position in the match. 
17.    return (textCursor - patternCursor)
18.  else
19.    return -1
Output: position in text if pattern is found, -1 if not found.


Algorithm: computeNextIndex (pattern)
Input: a pattern array of length m
1.   nextIndex[0] = 0
2.   for i=1 to m-1
3.     nextIndex[i] = largest suffix of pattern[0]...pattern[i-1] that
                      is a prefix of pattern.
4.   endfor
5.   return nextIndex
Output: the nextIndex array (representing the nextIndex function)

Analysis:

Since we never backtrack in scanning the text: O(n) for the scan.
Our implementation of computeNextIndex took: O(m²) time.
⇒ Overall time: O(m² + n)
It is possible to optimize computeNextIndex to take O(m) time.
⇒ Overall time: O(m + n)

5.4 The Boyer-Moore-Horspool Algorithm

The problems with previous algorithms:

KMP runs in time O(m + n), but is complicated and is inefficient for small patterns.
KMP does not exploit low-overlap between pattern and text.

The Boyer-Moore-Horspool algorithm:

It's a heuristic: runs in worst-case O(mn) time.
But is simple and effective in practice.

Key ideas:

Start comparisons from the right end of the pattern:
When a mismatch occurs, shift pattern to the right.
Ideal case: mismatch character in text does not occur in pattern at all
⇒ Entire pattern can be shifted to the mismatch position.
Less ideal case:
The rule at each step is:
- Start comparing from the right end of the pattern.
- Identify the mismatch char in the text, and its position.
- Find the rightmost occurence of this char in the pattern, that is to the left of the mismatch position.
- Move the pattern rightwards to align these two chars.

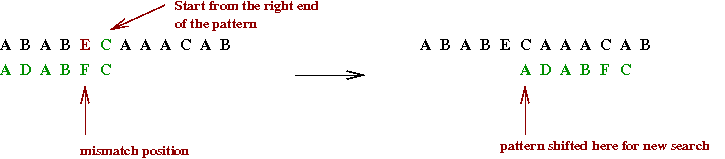
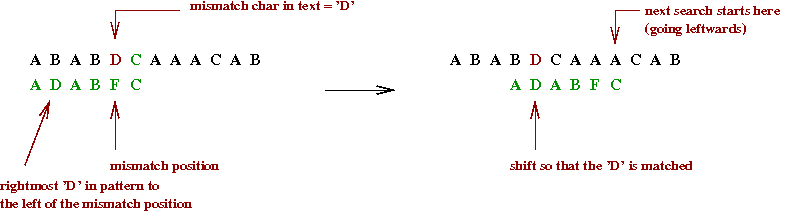
The worst-case running time is still O(mn), but it is easy to implement and practically fast.

5.5 Pattern Search with Deterministic Finite Automata

The "Evil Bureaucracy" metaphor:

Suppose you need to get a document (e.g., passport application) signed by various officials in sequence.
The officials:

OFFICIAL ABBREVIATION

Assistant Director A

Director D

Managing Director M

Chief Managing Director C
The paper trail:
Interpretation: going from "state" to "state"

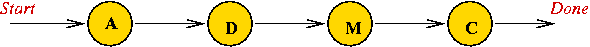
⇒ Here, "A" represents the state of "approval by A".
Consider this alternative scenario:
- Suppose your form needs to have one item satisfied for each bureaucrat.
- It is each bureaucrat's job to check that their item is on the form.
- Thus, "A" checks for the "A" item, "B" looks for the "B" item, and so on.
Then, the above "state machine" recognizes the pattern of items "A D M C".

What is a DFA?

DFA = Deterministic Finite Automaton.
A DFA is a collection of "states" and "arcs".
The arcs have "labels" on them.
A label on an arc is a "rule" that describes when one state leads to another.
A DFA scans an input string and follows labels accordingly.
Each input character causes a jump from the current "state" to the next "state"
⇒ Which can sometimes result in jumping from a state to itself
Some DFA "states" are marked as "final states".
If the input causes the DFA to go into a final state, the input is "accepted".

Example: consider a DFA to recognize the string "A B C D".

If the input string is "A B C D", the DFA goes into the final state.
- Initially we are in state 0.
- The first letter, "A", causes a jump to state 1.
- The next letter, "B", causes a jump from state 1 to state 2.
- ... and so on.
Note: there is an implicit "cursor" or position in the input string as we progress one character at a time.
Any other input string causes the DFA to end in a "non-final" state.

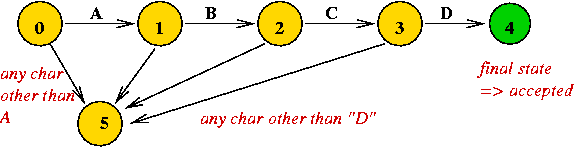
Two key questions about DFAs:

Given a DFA, what is the set of strings that will be "accepted" by the DFA (i.e., will reach a final state)?
Given a set of strings, can a DFA be constructed to "accept" only that set?

Example: consider this DFA

The DFA finds the pattern "A B C D" in the text "... (any number of E's) ... A B C D ... (anything else)".
The DFA does this when we feed it the text
"... (any number of E's) ... A B C D ... (anything else)"
Example text: "E E A B C D A E D C"
Here, we allow states to "get stuck" (not accept input).
Note:
- States are (typically) numbered 0, 1, ... etc.
- Input characters are "swallowed" (removed) one-by-one for each arc taken.

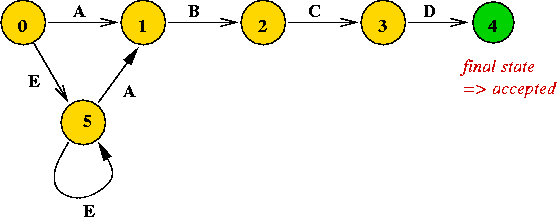
In-Class Exercise 5.4: Draw a DFA to find the first occurence of "A B C D" in a text consisting of the following structure: "... (zero or more E's) ... A ... (zero or more E's) ... B C D ... (anything)". Write the pseudocode equivalent of the DFA. That is, what does a DFA implementation in code (pseudocode) look like?

A DFA to find the first occurrence of "A B C D" in any text:

Here, the idea is to let state 5 "eat" non-A characters until the first "A" is found.
When an "A" is detected in other states, move to state 1.

Thus, a DFA can be used for the pattern search problem.

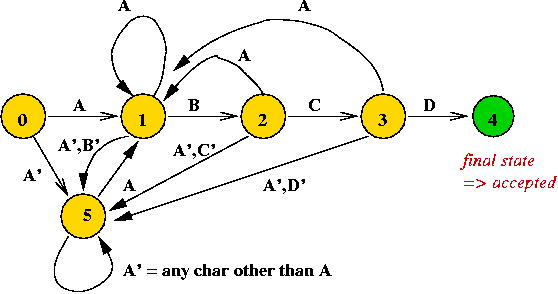
Another example: a DFA for the pattern "A B C A B D"

Note: only some arcs are shown.
Observe arc from state 5 to state 3
⇒ because the sub-pattern "A B" is already scanned.

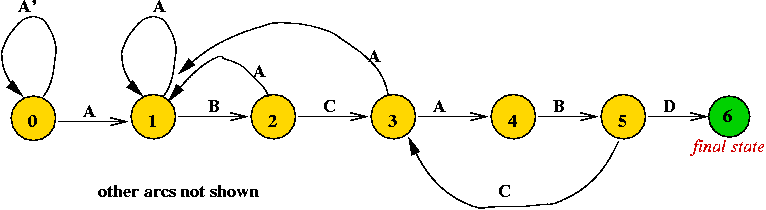
The nextState function:

A DFA is represented in a program using a "nextState" function (a table).
The table has one row for each state, one column for each possible input character.
The table entry for row i and column "C" tells you the next state going from state i upon input "C".
⇒ the arc leading out of i with character "C".

Example:

Suppose our character set is {A, B, C, D}.
The nextState function for the pattern "A B C A B D" is:

Input char

Current
state A B C D

0 1 0 0 0

1 1 2 0 0

2 1 0 3 0

3 4 0 0 0

4 1 5 0 0

5 1 0 3 6

Sample execution using text: "A A B C A B C A B D D"


 A A A B C A B C A B D          Processing 'A': next-state = 1


 A A A B C A B C A B D          Processing 'A': next-state = 1


 A A B B C A B C A B D          Processing 'B': next-state = 2


 A A B C C A B C A B D          Processing 'C': next-state = 3


 A A B C A A B C A B D          Processing 'A': next-state = 4


 A A B C A B B C A B D          Processing 'B': next-state = 5


 A A B C A B C C A B D          Processing 'C': next-state = 3


 A A B C A B C A A B D          Processing 'A': next-state = 4


 A A B C A B C A B B D          Processing 'B': next-state = 5


 A A B C A B C A B D D          Processing 'D': next-state = 6


 A A B C A B C A B D D          Pattern found
         A B C A B D

Building the nextState function:

Some observations:
- The nextState function uses the current character in the input.
- States can be numbered according to the length of the prefix detected so far.
- Forward arcs (low number to high-numbered state) go along the pattern itself.
- Reverse arc lengths depend on the length of the prefix detected so far.
- Key observation: a reverse arc decreases by the length of the largest suffix that is a prefix (of the pattern).
- The final state is numbered with the pattern length.

Pseudocode:


Algorithm: DFAPatternSearch (pattern, text)
Input: pattern array of length m, text array of length n
     // First, build the nextState function. 
1.   nextState = computeNextStateFunction (pattern)
     // Now scan input character by character. 
2.   currentState = 0
3.   for textCursor=0 to n-1
4.     character = text[textCursor]
       // Go to next state. 
5.     currentState = nextState[currentState][character]
       // If it's the final state, we're done. 
6.     if currentState = m
7.       return (textCursor - m + 1)
8.     endif
9.   endfor
10.  return -1
Output: position in text if pattern is found, -1 if not found.


Algorithm: computeNextStateFunction (pattern)
Input: pattern array of length m
1.   for state=0 to m-1
2.     for character=smallestChar to largestChar
3.       patternPlusChar = concatenate (pattern, character)
4.       k = length of longest suffix of patternPlusChar that is a prefix of pattern
5.       nextState[state][character] = k
6.     endfor
7.   endfor

Analysis:

The nextState function requires O(cm²) time to compute where c = size of character set.
Processing the text requires O(n) time.
⇒ total time is O(cm² + n).

In practice:

The DFA method is rarely used because character sets tend to be large
⇒ nextState computation is significant.
However, DFA's are easy to build and have many other applications
⇒ useful as library code.
DFA's can be automatically built using tools like Lex.

5.6 Wildcards, Regular Expressions and Non-Deterministic Finite Automata

What does "wildcard" mean?

Consider the Unix command to list files, used in the following way:
```
    ls *.java
   
```
Here, the "*" is equivalent to "any character string".
(Not containing special characters like "*").
The pattern *.java is a wildcard expression.
In simple text search, a pattern is one string.
A wildcard expression can specify a set of strings:
*.java = {.java, a.java, aa.java, aaa.java, ... ,b.java, ... (infinite) set}

Regular expressions:

Regular expressions are a generalization of wildcard expressions.
Think of a regular expression as a "way to describe a set of strings that satisfy a property".
Regular expressions are specified recursively using operators:
- Terminal: a character is a regular expression.
  Example: "A" is a regular expression.
- Concatenation: if R₁ and R₂ are regular expressions, so is R₁R₂.
  Example: "A" concatenated with "B" gives regular expression "A B".
- Or: if R₁ and R₂ are regular expressions, so is R₁ | R₂.
  - A | B is a regular expression specifying the set {"A", "B"}.
  - Since C is a regular expression, using concatenation, (A | B) C is a regular expression.
  - (A | B) C specifies the set {"A C", "B C"}.
- Closure (or Kleene-star): if R₁ is a regular expression, R₁^* specifies any number of repetitions of R₁:
  - Note: the * is used as a superscript and (confusingly) is NOT the same as the wildcard "*".
  - The expression A^* specifies the set {"A", "A A", "A A A", ...(infinite set)} and the empty string.
  - Similarly, (AB)^*C = {"C", "A B C", "A B A B", ... }.
The alphabet and expression operators.
- Underlying both wildcard expressions and regular expression is an alphabet
  ⇒ the characters used as terminals.
- Operators used for expressions, such as | and ^* are NOT permitted to be in the alphabet.
Expressing wildcards with regular expressions:
- Suppose our alphabet consists of {A, B, C}
- Consider the wildcard expression "* A B *".
- The corresponding regular expression is: (A | B | C)^* (A B) (A | B | C)^*
- Intuition: any combination of letters, followed by A B, followed by any combination of letters.
Terminology: the following are equivalent
- A C satisfies expression (A | B) C
- A C matches expression (A | B) C
- A C is in the set specified by expression (A | B) C

In-Class Exercise 5.5: Construct the regular expression for the set {"D A B", "D A C", "D A B E", "D A C E", "D A B E E", "D A C E E",... }

The pattern-search problem we want to solve:

Given a regular expression, e.g., (A | B) (A B)^* C, and a text, find the first occurrence of a substring in the text that satisfies the regular expression.
(i.e., is in the set specified by the expression).
- Example: regular expression (A | B) (A B)^* C, and text "D B B A A B C D A".
- The substring "A A B C" in "D B B A A B C D A" satisfies in the expression.
First, we'll solve a simpler problem: Given a regular expression and a string (pattern), does the string satisfy the expression?
We'll use a Non-Deterministic Finite Automaton (NDFA) to recognize strings that match a regular expression.

What is an NDFA?

First, recall that our DFA examples were built to recognize a single pattern (string).
We can construct a DFA to recognize strings from a set:
- Consider the set {"A B C", "A D E"}
- This DFA recognizes the set:
- Note: there are multiple final states.
Consider a DFA (separately) for each string in {"A B C", "A D E"}

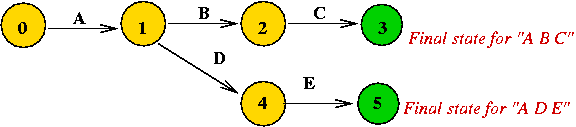
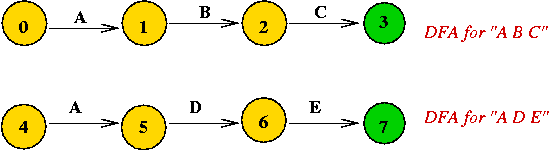
(States are numbered differently, to avoid confusion).
Now, combine them into an NDFA:
- The NDFA has "special states" that allow non-deterministic jumps to other states.
- A jump from a "special state" does NOT swallow an input character.
- The NDFA can pick any outgoing arc from a "special state".
- The non-special states are called "regular" states.
- Regular states must swallow input.
- For a particular input character, there is only one state to go to from a regular state.
What does "choice" really mean?
- Think of the NDFA faced with a choice of two arcs (in a special state).
- The NDFA makes a clone of itself.
- The original follows one arc.
- The clone follows the second arc.
- Thus, for multiple arcs, there are multiple clones.
  ⇒ a family of NDFA's operate on input (in parallel).
- If any one of the NDFA's reach a final state, the input string is "recognized".
- Think of each clone as a "thread" running on its own.

Example:

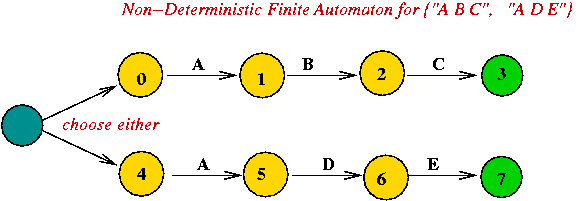
Constructing an NDFA from a regular expression:

Recall original goal: a recognizer for regular expressions.
The NDFA will be constructed recursively using combining rules.
Rules:
- Terminal: An NDFA for a single character, e.g., for "A"
  - Special states are used as start and end states.
  - A regular state is used to recognize the character.
- Concatenation:
  - Suppose we have NDFA's for regular expressions R₁ and R₂
  - We want the NDFA for R₁ R₂
  - The NDFA's are combined in sequence by merging the final state of R₁ and the start state of R₂.
- Or:
  - Suppose we have NDFA's for regular expressions R₁ and R₂
  - We want the NDFA for R₁ | R₂
  - The NDFA's are combined in "parallel" by introducing new special states.
- Closure:
  - Suppose we have an NDFA for regular expression R₁.
  - We want the NDFA for R₁^*.
  - Add new start and final states, and new arcs (arrows).
Optimizations:
- The above combination rules will result in "bloated" NDFA's.
- Several optimizations can be applied, for example:
  - Special states in sequence:
  - Removing the special start state for a single-character.

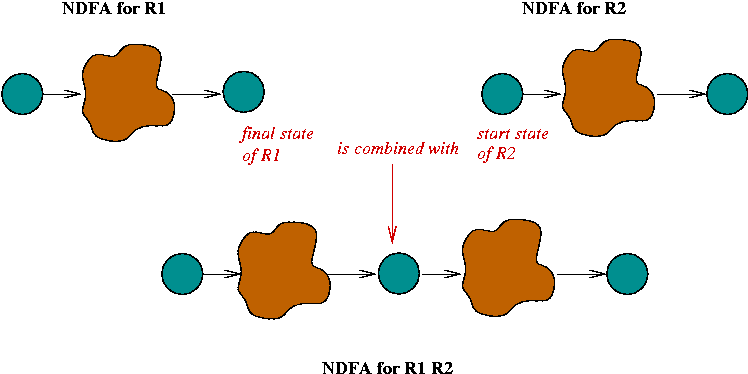
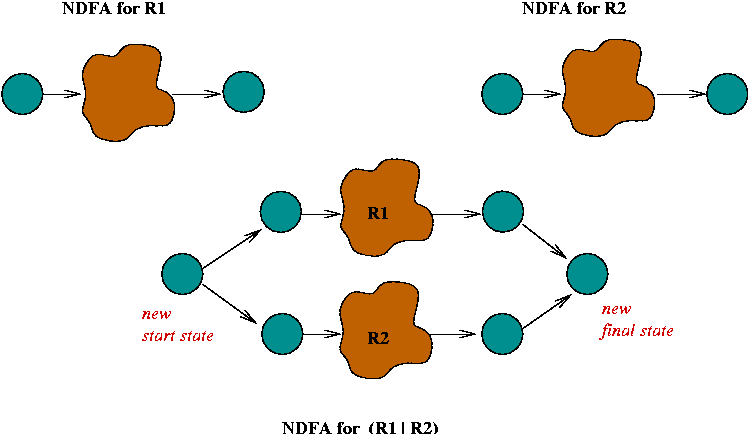
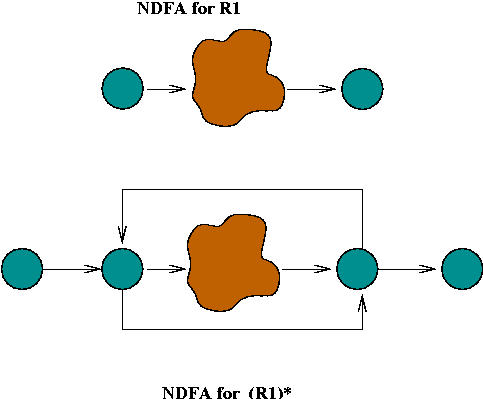
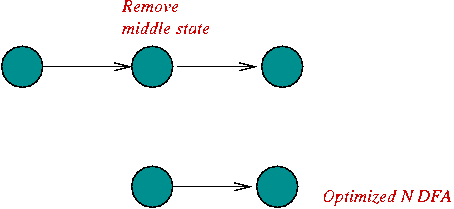
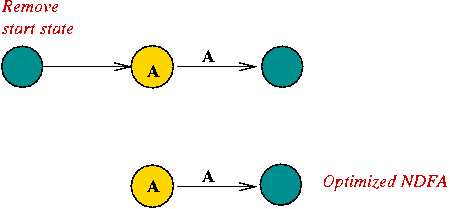
In-Class Exercise 5.6: Construct an NDFA for the regular expression "C (A | B) (A B)^*". First, use the rules to construct an unoptimized version, then try to optimize it (reduce the number of states).

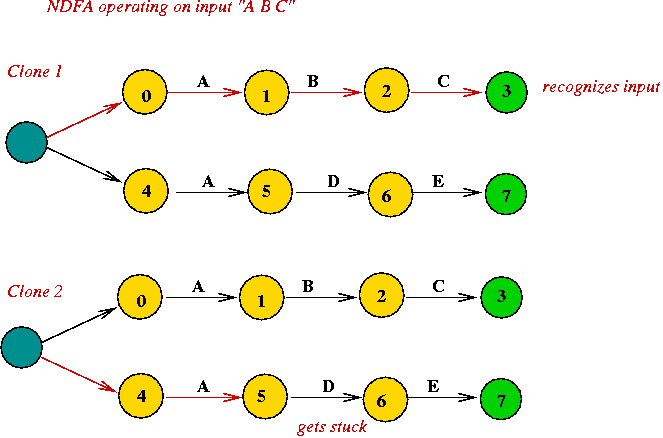
Two ways to "run" an NDFA on input:

Use threads:
- For each "clone", fire off a thread that starts the new clone with the appropriate "choice" made (one thread per choice).
- If any thread reaches a final state, the string is accepted.
- If any thread gets stuck, it stops.
Use a single thread and a deque (a double-ended queue).

Using a deque:

Track all possible states in clones simultaneously.
When processing a "special state", place all possible next states in the front of the deque.
When processing a regular state, consume the input character, and place next state at the end of the queue.
Keep processing until either:
- A final state is reached
  ⇒ accept input string.
- All input is consumed
  string does not satisfy regular expression.

In-Class Exercise 5.7: This is a recursion-writing exercise. Write pseudocode describing a recursive algorithm to see if a given string (such as PatternSearch.java) matches a given wildcard pattern (such as Patt*nSearch.*). Your algorithm should solve the problem directly, without using DFAs or NDFAs.

5.7 Web Search Engines

In this section, we'll give an overview of how search engines work.

Three parts to search engines:

Crawling:
- The process of scouring the web looking for new documents.
- Usually, by retrieving a page and then following links in it.
- Typically non-recursive, with priorities.
  ⇒ keep separate list of "well-known" sites.
- Crawling is independent of other processes.
- Easy to parallelize.
Indexing
- Key idea: build an inverted list over document base.
- Also collect/compute information used in relevance-ranking.
Query handling:
- Present a web-page for users with query fields, e.g., Google's simple homepage.
- Extract query and parse it.
- Compute/extract results (links to documents).
- Sort results by relevance or other factors.
- Display (send back to browser).

In-Class Exercise 5.8: Look up the "page rank" algorithm and describe how it works. What are the disadvantages of using that algorithm?

Indexing via an example:

Consider these two documents:
An inverted list:
- Simply a collection of all "words" with pointers to documents that contain them:
Key ideas in processing a document:
- Skip "stop words" such as "the, an, a,...".
- Maintain positions of important words.
- Add data to inverted list.
- Other info: statistical data
  (e.g., number of occurrences in document).

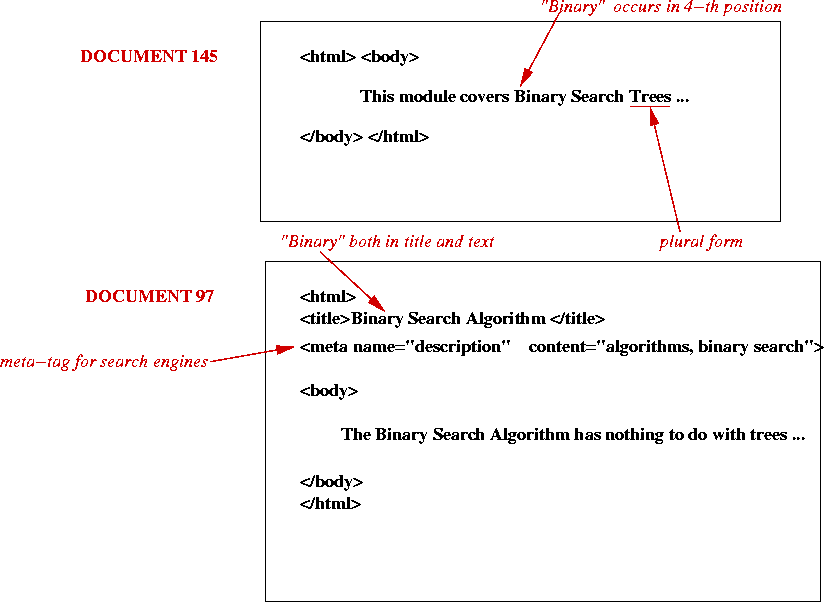
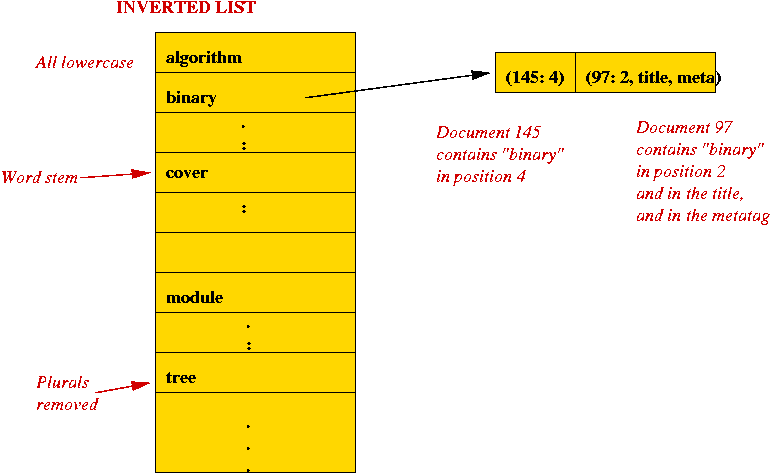
Query-handling:

Example: "Algorithm"
- Find all documents containing word.
- Rank according to relevance.
  ⇒ rank Document 97 higher than Document 145 (because "Algorithm" is in the title).
Example: "Binary Search Tree".
- Find all documents containing the words.
- Identify those containing all three words.
- Rank according to relevance.
  ⇒ rank Document 145 higher than Document 97 (because the words occur in sequence).

Mismatch Position	nextIndex
0	0
1	0
2	0
3	1	(Infer: match up to 0)
4	2	(Infer: match up to 1)
5	3	(Infer: match up to 2)

	OFFICIAL		ABBREVIATION
	Assistant Director		A
	Director		D
	Managing Director		M
	Chief Managing Director		C

	Input char
Current state	A	B	C	D
0	1	0	0	0
1	1	2	0	0
2	1	0	3	0
3	4	0	0	0
4	1	5	0	0
5	1	0	3	6