Chapter: Graph Theory -- A valuable mathematical model

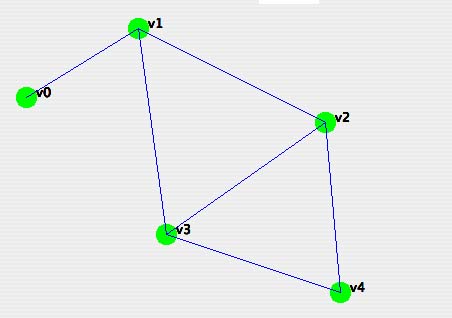
A graph is a set of Nodes and a set of Edges. The terms node and vertex are used interchangeably. Each edge consists of a pair of Nodes. We draw pictures of graphs with disks representing the points and lines representing the edges.

The number of edges containing a particular vertex is called the degree of the vertex. For example, v3 has degree 3. v0 has degree 1. If nodes are joined by an edge, we say the two nodes are adjacent.

Graphs can represent all sorts of data. For example, the nodes v0 v1 v2 v3 v4 might represent five people. The edges might denote a relationship such as "knows". In that case, the graph conveys a lot of information, such as:

• v1 v2 and v3 all know each other
• v2 v3 and v4 all know each other
• the largest group of "mutual acquaintances" consists of three people
• v0 only knows one other person
• v4 knows exactly two other people
• v1 v2 and v3 each know three other people

If we are interpreting a graph in this way, i.e. as a set of people and a set of binary relationships between the people, we sometimes speak of the graph as representing a social network.

Graph theory encourages us to make definitions of concepts within social networks. For example, since "degree" is an important concept in graph theory, we are likely to interpret that concept in the social network. The degree of a node corresponds to the number of acquaintances the person represented by the node has. In social networks therefore we might be tempted to define the acquaintance-count of a person. This is simply the degree of that person's node. Two adjacent nodes correspond to acquaintances. Two non-adjacent nodes correpond to a pair of people who don't know each other.

Graph theory encourages us to prove theorems about social networks. Such as:

Theorem: In any social network, if we sum the acquaintance-count over all the people, we will obtain an even number.

Proof:

1. Each edge contributes one to the acquaintance count of exactly 2 people.
2. Therefore the sum of the acquaintance-counts is exactly twice the number of edges.
3. ... which is an even number.
4. Q.E.D.

I am going to ask you to do something I've never asked you to do before in a lab; I'm going to ask you to write a mathematical proof. This is a CS class, so the graders will not be as exacting as a mathematics professor would be. Nevertheless, your proof should consist of a series of logical statements that, taken in sequence, will convince a reasonably intelligent person of the truth of your assertion.

Exercise 1

Theorem: In any social network, the number of people who have an odd number of acquaintances must be even.

If you liked that, try this optional exercise:

Exercise 2

• There are three mutual acquaintances (i.e. three people who all know each of the other two), or
• There are three mutual strangers (i.e. three people, no two of which know each other.