Chapter: Abstraction
...Section: Interfaces
... ...Subsection: The Persian Rug algorithm

A persian rug is a square whose side has length $2$n + 1 pixels, for some value of n (for example, 3, 5, 9, 17, ... 129, 257, 513, ...). Each pixel in the rug is drawn with a different color determined by the algorithm. We start with a list of all the colors to be used in coloring the rug. It can have any length, but more interesting rugs will arise if we include a larger number of colors. The basic idea of the algorithm is to use the colors on the border of the square to determine a color for dividing the square into four sub-squares, and then recursively repeating the algorithm.

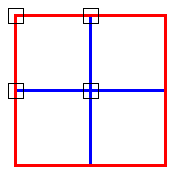
It works something like this: say the square to be divided has a red border, as pictured on the left below.

We consider the colors at the 4 corners, in this case all red, and compute a new color. Suppose the new color is blue. We divide the square into 4 squares with a pair of blue lines, as shown below left. We then repeat the algorithm on the 4 new squares (now with both red and blue borders), as shown below right. For these recursive calls the colors at the corners will be 2 reds and 2 blues.

Here is the algorithm in pseudocode:

LET colList = a list of colors
LET S be a square of size 2n + 1 for some n greater than 1
LET newColor be a function that takes four colors and returns a color

Color the border of the square one of the colors
Perform persianRug on S

persianRug(square S){

   if (S is 2 X 2){
      done
   }
   else {
      Get the four colors at the corner of the square;
      LET newCol = newColor(the four corner colors);
      Divide this square into four equal squares using newCol;
      Do persianRug on the four new squares;
   }
}