Chapter: The Koch Snowflake Curve

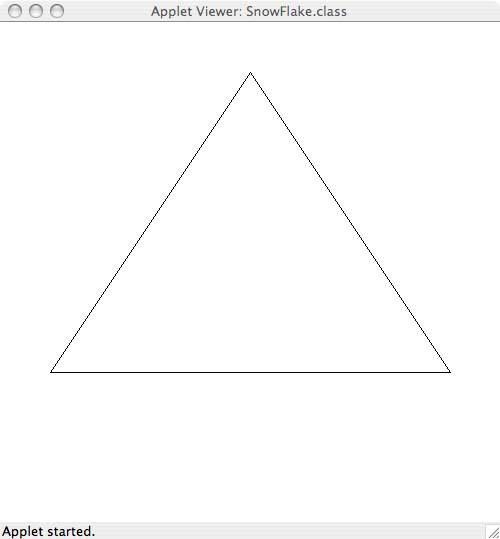
Consider this picture of a triangle.

What would happen if we replaced each line by a zigzag line that traces the first third of the line, zigs left at $60o$ for the same length, zags right at $60o$ for the same length again and then finally completes the last third of the original line? Imagine it and then look at this:

We get a star.

Now let's repeat the process and replace each line with a 4-segment zig-zag again:

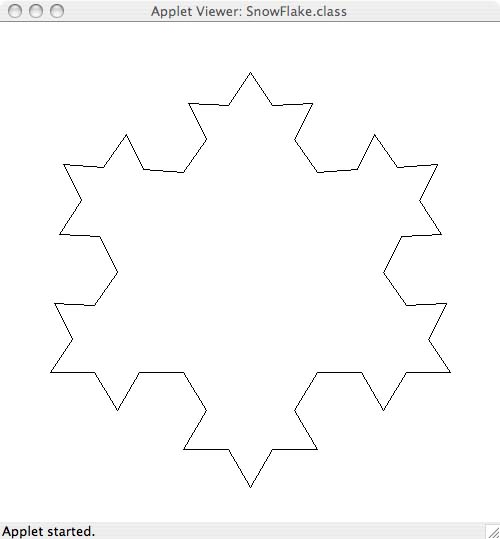
It begins to look like a snowflake doesn't it? Click in this applet to see the process animated.

        
             
            Your browser is ignoring the <APPLET> tag!      
        

Click again to repeat the process. If we had the screen resolution to repeat the process infinitely often, we would be approaching a fractal curve. For more information on fractals, do a Google search or visit the library or a bookstore and check out books like James Gleick's Chaos or the Computational Beauty of Nature or Mandelbrot's The Fractal Geometry of Nature or a host of others.

Fractal curves have interesting properties. Let's say we start with a triangle each of whose sides has length 1 metre. After the first zigzag operation, each side is replaced by 4 segments each of whose lengths is one third the length of the original side. So the triangle with three sides of length 1m becomes a star whose perimeter is $3\; *\; (4/$₃). At the next stage, each line segment gets replaced by four line segments each of length one third the length of the segment. So the perimeter again gets increased by a factor of $(4/$₃).

The length of the perimeter starts at 3. After one zigzag operation each side becomes $4/$₃ its previous size. After two zigzag operations the length will again multiply by $4/$₃. And so on. The total length of the perimeter goes from

$3$ to $3*(4/$₃) to $3*(4/$₃)*(⁴/₃) or $3*(4/$₃)²

Then with more repetitions to

$3*(4/$₃)³ and $3*(4/$₃)⁴ and $3*(4/$₃)⁵ and ...

But notice that the entire curve will always be contained inside the applet frame. This means that, no matter how many repetitions we make, the total area inside the snowflake curve will always be finite.

Exercise 1

1. In the limit, as the number $n$ of repetitions approaches infinity, what happens to the length of the snowflake curve?
2. In the limit, as the number $n$ of repetitions approaches infinity, what happens to the area enclosed inside the snowflake curve?
3. Imagine that you have a powerful microscope and can view one of the line segments within the curve as it exists after 42 repetitions. It will be, of course, a straight line segment.
   1. What is the length (in metres) of that line segment? You may use an expression of the form $(a/$_b)ⁿ, or you may try to extract an answer from a calculator.
   2. What would you see (in your microscope) replacing that line segment at the 43rd repetition?