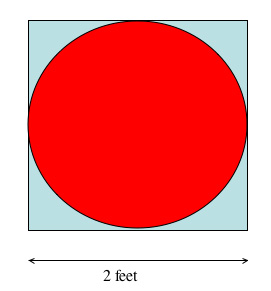
Using simulation to estimate the value of PI

Chapter: Using simulation to estimate the value of PI

Imagine a circular dartboard of radius 1 foot mounted on a square backdrop of side 2 feet. Now suppose darts are thrown. Of the darts that land within the square, some will land inside the circle of the dartboard (hits) and others will lie outside the circle but inside the square (misses).

Imagine the dartboard centered on a cartesian grid with its center at (0,0). Select two floating point numbers x and y both in the range from -1.0 to 1.0. $(x,y)$ are the coordinates of a dart randomly thrown that lands within the square. Sometimes, the dart will also be within the circle.

Q. 2: How can you tell if the point $(x,y)$ is inside the circle?

You can write a program to simulate throwing darts. Furthermore, it can count how many darts land within the dartboard. If you throw enough darts, the ratio of ^hits/_{total darts} will begin to approximate the probability that a random dart will land inside the circular dartboard.

Q. 3: What is the area of the dartboard?

And we know that the area of the square is 4 square feet.

Q. 4: What's the probability that a random dart lands in the dartboard?

Now you're ready to estimate the value of PI using simulation.

Exercise 4

Write a program to simulate throwing darts at the square-mounted dartboard pictured. It should keep track of how many are thrown, how many are hits, and the corresponding estimation of the value of PI. It should also pause occasionally to update the user and decide whether or not to continue. Here is a typical output:

>  simpi
78 hits in 100 throws for PI value 3.120000
Hit q to quit, ENTER to continue > 
155 hits in 200 throws for PI value 3.100000
Hit q to quit, ENTER to continue > 
231 hits in 300 throws for PI value 3.080000
Hit q to quit, ENTER to continue > 
310 hits in 400 throws for PI value 3.100000
Hit q to quit, ENTER to continue > 
391 hits in 500 throws for PI value 3.128000
Hit q to quit, ENTER to continue > q

rhyspj@gwu.edu