Chapter: Parsing and Unparsing

Whenever an interpreter interprets a given piece of input, two things need to happen. First, the input needs to be parsed, or separated out, into its component parts in such a way that the parts can be easily worked with. Then the interpreter can go about its job of interpreting. The parsing deals with the syntactic considerations, and the interpreting deals with the semantic considerations.

Q. 3

Why do we need to separate out these two steps? Can't we just combine them together?

The actual syntax that a programmer writes when working in a programming language like Scheme or Java is known as a concrete syntax. The syntax generated by a parser and used by an interpreter is known as an abstract syntax. Before we generate a parser, then, we need to decide on an abstract syntax, and how it will be represented. We will work with a small subset of Scheme defined by the grammar below.

<exp> ::= <number>		
        | <varref>		  
        | (lambda (<var>) <exp>)  
        | (<exp> <exp>)		  

This grammar can work with numbers, variable references, lambda expressions of one variable, and applications of one expression to another.

In order to make an abstract syntax for this grammar, we need to decide on a name for each production in the grammar, and names for each nonterminal in the production. One possible choice is

<exp> ::= <number>                    lit (datum)
        | <varref>                          varref (var)
        | (lambda (<var>) <exp>)      function (formal body)
        | (<exp> <exp>)               app (rator rand)

(In this example, rator stands for operator and rand stands for operand.)

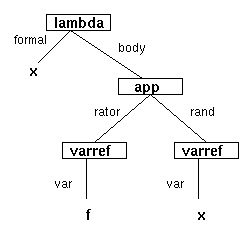
It is easiest to reason about an abstract syntax representation as an abstract syntax tree. As an example, the abstract syntax tree for the expression (lambda (x) (f x)), following the specification above, looks like this.

Chez Scheme provides a define-record-type form that creates for us:

• a constructor procedure
• a type predicate that returns true only for records of the type,
• an access procedure for each field
• (and an assignment procedure for each mutable field -- this is a feature we won't be using)

We will use define-record-type to represent each of the four productions of our grammar above. We will associate with each production name a record type, and the fields in the record type will correspond to the names of the nonterminals. Here are the record definitions we will use:

(define-record-type lit (fields datum))
(define-record-type varref (fields var))
(define-record-type function (fields formal body))
(define-record-type app (fields rator rand))

As you can tell if you read the section above from the Chez Scheme User's Guide, the first of these results in the definition of:

• a constructor called make-lit
• a type predicate named lit?
• an accessor called lit-datum
• (but not a mutator called set-lit-datum because we did not declare datum to be a mutable field)

Look at this transcript to see what the last of the define-record-types above achieves:

; from  (define-record-type app (fields rator rand))
> make-app
#
> (define foo (make-app 'plus 99))
> (app? foo)
#t
> (app? +)
#f
> (app-rator foo)
plus
> (app-rand foo)
99
> 

The code above is intended to demonstrate the define-record-type form. As a matter of fact (make-app 'plus 99) does not result in a piece of syntax that is valid in the language we are about to define.

Although it's not standard Scheme, define-record-type is immensely useful in helping us create the structures needed for an abstract syntax. In particular, a parser can be defined very easily. The code can be found in parse.ss.

If you know the concrete syntax of the language, the parser almost writes itself! If you don't agree with me, then look at the syntax and the Scheme code close to each other:

<exp> ::= <number>                    lit (datum)
        | <varref>                          varref (var)
        | (lambda (<var>) <exp>)      function (formal body)
        | (<exp> <exp>)               app (rator rand)


(define parse
  (lambda (datum)
    (cond
     ((number? datum) (make-lit datum))
     ((symbol? datum) (make-varref datum))
     ((pair? datum) (if (eq? (car datum) 'lambda)
                        (make-function (caadr datum) (parse (caddr datum)))
                        (make-app (parse (car datum)) (parse (cadr datum)))))
     (else (error 'parse "Invalid concrete syntax" datum)))))

Q. 4

What about all those yucky "magic number" caddr cadr caadr things?

It is sometimes useful to be able to unparse something represented in abstract syntax. It is equally easy to write unparse in Scheme. The code can be found in unparse.ss.

Exercise 1

> (parse 44)
#[#{lit bh76vhxsbantq4gv-1} 44]
> (parse 'x)
#[#{varref bh76vhxsbantq4gv-2} x]
> (parse '(lambda (x) x))
#[#{function bh76vhxsbantq4gv-3} x #[#{varref bh76vhxsbantq4gv-2} x]]
> (unparse (parse '((lambda (x) x) 42)))
((lambda (x) x) 42)
>

> (unparse (parse '((lambda (x) x) 42 45)))
((lambda (x) x) 42)
> (unparse (parse '((lambda (x y) x) 96 1 2)))
((lambda (x) x) 96)
> 

You need not hand in anything for this exercise. However, you should play enough with parse and unparse that you understand them well. You should be able to make sense of that strange #[...] notation and those uniquely "gensym'ed" names. Can you explain what will happen if you try to parse the application of a function of 2? Think about how to modify the parser to check for this kind of violation so that you can enforce the details of your syntax. Try to make up other predict/test examples of your own. The idea here is for you to take the time and really understand this parsing process. Ask your friendly lab instructor if you're unsure about any details here.

> (define g (parse '(lambda (x) (f x))))
> g
#[#{function bh76vhxsbantq4gv-3} x #[#{app bh76vhxsbantq4gv-0} #[#{varref bh76vhxsbantq4gv-2} f] #[#{varref bh76vhxsbantq4gv-2} x]]]
> (unparse g)
(lambda (x) (f x))
> (parse 'x)
#[#{varref bh76vhxsbantq4gv-2} x]
> (unparse #[#{varref bh76vhxsbantq4gv-2} x])

Exception: invalid syntax #[#{varref bh76vhxsbantq4gv-2} x]
Type (debug) to enter the debugger.
> (unparse '#[#{varref bh76vhxsbantq4gv-2} x])
x
> (unparse (parse '(lambda (x) (lambda (t) (t ((lambda (x) p) z))))))
(lambda (x) (lambda (t) (t ((lambda (x) p) z))))
> 

For the next exercise, I recommend you exit scheme and start it again. That's so there will be no lingering define-record-type definitions around to haunt you. I created parse2.ss and unparse2.ss by editing parse.ss and unparse.ss; but you can start from scratch if you prefer.

Exercise 2

Here is an extension of the grammar used in this section:

<exp> ::= <number>			lit (datum)
        | <varref>			varref (var)
	| (if <exp> <exp> <exp>)	if (test-exp then-exp else-exp)
        | (lambda ({<var>}*) <exp>) 	lambda (formals body)
        | (<exp> {<exp>}*)		app (rator rands)

Notice the changes. We now allow functions of arbitrary arity. We have added an if statement. Whereas you can simply parse or unparse a single operand, you may want to use map to get over a list of them?

1. Write parse-2, a parser for this grammar.

(Note I have been nice to you and indented the parsed code. Your results will be messier.)

> (parse-2 '(lambda (x) (+ x 2)))
#[#{function bh76vhxsbantq4gv-4} (x) 
  #[#{app bh76vhxsbantq4gv-5} 
    #[#{varref bh76vhxsbantq4gv-6} +] 
    (#[#{varref bh76vhxsbantq4gv-6} x] #[#{lit bh76vhxsbantq4gv-8} 2])]]
> (parse-2 '(if (happy? me) (smile me) (frown me)))
#[#{if bh76vhxsbantq4gv-7} 
  #[#{app bh76vhxsbantq4gv-5} 
     #[#{varref bh76vhxsbantq4gv-6} happy?] 
     (#[#{varref bh76vhxsbantq4gv-6} me])] 
  #[#{app bh76vhxsbantq4gv-5} 
     #[#{varref bh76vhxsbantq4gv-6} smile] 
     (#[#{varref bh76vhxsbantq4gv-6} me])] 
  #[#{app bh76vhxsbantq4gv-5} 
     #[#{varref bh76vhxsbantq4gv-6} frown] 
     (#[#{varref bh76vhxsbantq4gv-6} me])]]
> (parse-2 '( (lambda (x y z) (* x y (+ z 1))) 2 4 (expt 4 5)))
#[#{app bh76vhxsbantq4gv-5} 
  #[#{function bh76vhxsbantq4gv-4} (x y z) 
    #[#{app bh76vhxsbantq4gv-5} 
      #[#{varref bh76vhxsbantq4gv-6} *] 
        (#[#{varref bh76vhxsbantq4gv-6} x] 
         #[#{varref bh76vhxsbantq4gv-6} y] 
         #[#{app bh76vhxsbantq4gv-5} 
            #[#{varref bh76vhxsbantq4gv-6} +] 
            (#[#{varref bh76vhxsbantq4gv-6} z] 
            #[#{lit bh76vhxsbantq4gv-8} 1])])]] 
  (#[#{lit bh76vhxsbantq4gv-8} 2] 
   #[#{lit bh76vhxsbantq4gv-8} 4] 
   #[#{app bh76vhxsbantq4gv-5} 
     #[#{varref bh76vhxsbantq4gv-6} expt] 
       (#[#{lit bh76vhxsbantq4gv-8} 4] 
        #[#{lit bh76vhxsbantq4gv-8} 5])])]
> 

2. Write unparse-2.

> (load "parse2.ss")
> (load "unparse2.ss")
> (unparse-2 (parse-2 '(lambda (x) x)))
(lambda (x) x)
> (unparse-2 (parse-2 '(lambda (x) (+ x 2))))
(lambda (x) (+ x 2))
> (unparse-2 (parse-2 '((lambda (x y z) (* x y (+ z 1))) 2 4 (expt 4 5))))
((lambda (x y z) (* x y (+ z 1))) 2 4 (expt 4 5))
> 

It should be clear now that abstract syntax is not meant for human consumption. However, when writing a program that deals with syntax such as an interpreter, it is much easier to use a well thought out abstract syntax than to work directly with the concrete syntax.

Some good news. At this stage you have developed a fairly impressive parser and unparser. You will need those skills in Labs 5 and onwards. But for the rest of this lab, you will work with much simpler parsers and unparsers. Don't forget what you learned, though!