Chapter: Finding Continuations
...Section: Tail Recursion
... ...Subsection: Proper Tail Recursion

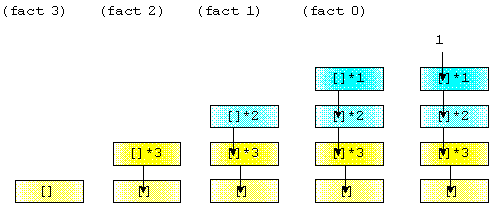
Why are we interested in tail recursive calls? Because they are cheap. Consider the mechanics of executing (fact n). With each recursive call the context becomes bigger. That context must be saved somehow or else we lose the computation. The execution stack exists for exactly this purpose. Every time a function is called a new frame containing the current execution state is pushed on the stack. This frame is restored when control returns from the call. Altogether, the collection of frames on the stack constitutes the current continuation.

The following diagram shows how the stack models the context dynamics of (fact 3).

Now, consider a tail recursive program, like islat. If a frame is likewise pushed on the stack for each recursive call, you get something like this.

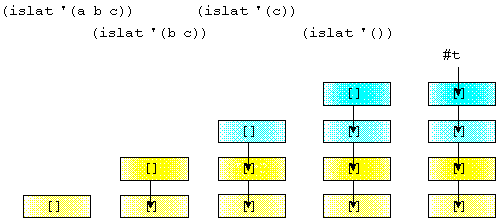
This outcome is consistent with the definition of tail recursion, but is clearly a waste of effort. In an efficient implementation, a tail recursive call ignores the stack and simply begins executing the code corresponding to the call. Such an implementation is called proper tail recursion.

Now compare once again the while loop and its recursive counterpart from before.

Q. 8

Is there a uniform relationship between iteration and tail recursion?

This gives us a precise definition of iteration: a repetitive program that does not create a growing context on the stack; in other words, a properly tail recursive program.

Exercise 5

1. A proper tail recursive call to G never returns to its caller F, yet the computation can proceed as though it had.
2. From the point of view of control, a proper tail recursive call is equivalent to a .