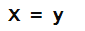Lecture Notes 03: Introduction to Numeric Variables

Objectives

By the end of this module, you will be able to:

Create variable declarations.
Assign values to variables by simple assignment, and print them out.
Demonstrate ability to perform operations on integers for a desired output.
Simplify expressions with constants to single value.
Evaluate expressions with variables in them.
Convert English descriptions of operations into expressions.
Trace execution with expressions and calculations.
Identify new syntactic elements related to the above.
Convert values by using Casting.
Demonstrate how to read values entered by the user into the terminal.

And, once we've worked with integers, we'll also do some "number crunching".

Shift in course format

We are going to start picking up the pace in both lectures and labs at this point in the semester. Some items to be aware of:

We will be spending class time going over coding exercises
You will have homework exercises you are expected to complete and submit to BB; we will start these in class
We will also often go over sample quizzes in class as well
Labs will be used to 1) proctor quizzes (using LockDown Browser and Blackboard) and 2) work on the coding exercises mentioned
Therefore, you should plan to spend 3-5 hours a week outside of lectures and labs working on coding exercises

Why are numbers and numeric types useful in computation?

Control systems using mathematical calculations, like SpaceX
Articial Intellgience and Deep Learning: billions of numeric calculations to train these models
Other examples?

Now, let's talk about how Java (and other programming languages store the most basic type of values: numbers.

But first, an analogy

Suppose we have boxes. Consider the following rules about "boxes":

Each box can store only one item.
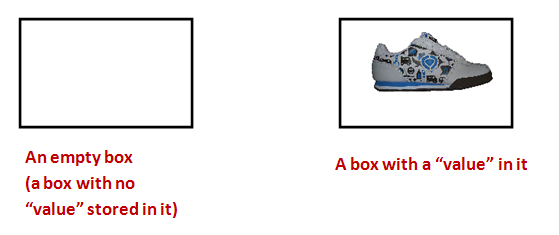
The possible things that can be stored inside are called values.
Thus, at any given moment, a box's value is whatever's inside it.
Each box is "typed"
⇒ What this means:
- A box meant for shoes is allowed to store only shoes.
- A box meant for caps is allowed to store only caps.
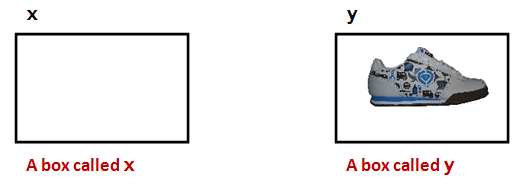
Each box has a unique name:
There is a cloning process that works like this:
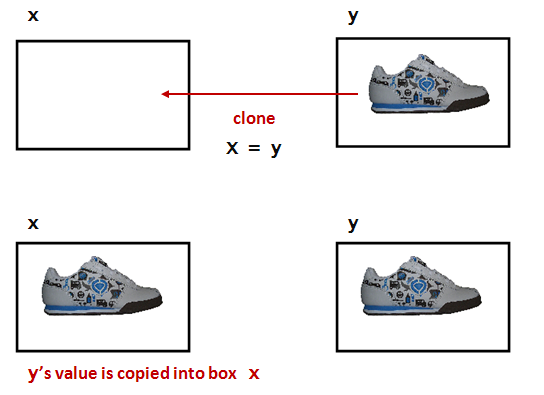
- The value inside one box is cloned.
- The cloned value is placed inside another.
There is a strange shortcut notation to specify cloning:
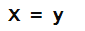
- Here, the = (equals sign) does NOT mean "equals."
- It has been repurposed to mean "clone", "copy," or, in programming-language jargon, "assign".
- Notice that what happens is whatever is in the box that y points to, gets copied into the box that x points to. This is one of the most important, fundamental concepts we will cover in this course, though it seems deceptively simple. You'll hear me say all semester long, "copy what's in the box". We will ALWAYS do a "copy what's in the box" when we are doing any type of assignment -- remembering this will make your lives much easier this semester!
How to say it: "x is assigned the value in y".
Important: Remember, a box can hold only one value at a time.

Integer variables

Consider the following program:

Activity 1:Let's trace through this code together to make sure you understand the following concepts about creating and using integers in Java:

Every variable in Java must be declared with a type.
The compiler will then enforce that all assignments to that variable are the type we declared it to be.

Some notes on style:

It is good practice to put a space before and after your operators for readability.
Similarly, you should generally strive for meaningful variable names. We'll enforce this this semester by ensuring that all of your variable names are at least three letters long (unless they are a counter variable, which we will cover later).

Integer operators

Binary Operators

First, let's examine the familiar binary operators (you've already seen the addition operator above):

Addition: +
Subtraction: -
Multiplication: *
Division: /
Modulus: %

Most of these work the way you would expect them to on integers. However, integer division is a bit tricky, since it's possible to divide two integers and not have a whole number as the result (such as 5 / 2). In Java, however, the compiler sees that that only integers are being used, and will perform integer division. That is, the result is rounded down to the nearest integer. Thus, 1/4=0 and 21/6=3. Later, when we work with real numbers, we will see that, to compute a real-valued expression, at least one of the numbers needs to be real-valued (i.e. 5.0 / 2.0 = 2.5)

The modulus (%) operator is probably new for you, and it is used to return the remainder of a division. For example, 5 % 2 evaluates to 1, while 6 % 2 evaluates to 0, because there is no remainder.

When evaluating complex arithmetial expressions, such as 5 + 3 * 2, Java uses the same order of operations as you're used to, and evaluates left-to-right. To be sure, I recommend you use parentheses explicitly to make this order of evaluation and precedence obvious or as needed: (5 + 3) * 2

There are also some binary operators to check for equality:

is equal: ==
is not equal: !=
greater than, greater than or equal: >, >=
less than, less than or equal: <, <=

These work the way you would expect.

Unary Operators

Next, let's consider some unary operators:

These are operators that apply to a single variable.
For example:

Activity 2: Let's trace through this code in the Visualizer.
For example:

It is very important to know that a unary operator written like this:
num++;
will increase the value of the variable num by 1 only AFTER it has been resolved and used in the expression it is in.
That means that a more complex operation, that involves the unary operators, might not result in what you expect.

When things go wrong

As you might imagine, there are many ways to inadvertently create errors.

Let's start by identifying compilers errors by reading carefully.

Activity 3: Identify the compiler error:

Real-valued variables

About real numbers:

We typically think of real numbers as numbers "with something after the decimal point" like 3.14159 or 2.718.
But 3, an integer, is also a real number -- 3.0.
The "reals" are a much larger set, and include the integers.
Some tidbits about the reals:
- Some are rational meaning they can be expressed as a fraction of integers like 4/3.
- Others are irrational and cannot be expressed as such, such as √2.
- Some are transcendental, such as π.
So, is every number a real number?
⇒ No, there are numbers like √-1 that are imaginary.

Just like we did with integers, we can declare variables and assign values to them, using the reserved word double

The short form int corresponds nicely with the English word integer. But double? There is an explanation (below).

One can also use the Java reserved word float as a substitute for double, as in:

float x = 3.14159;

Here, float means English term floating point number.

Think about this:

A number like π has an infinite number of digits after the decimal (as do all irrationals and transendentals).
Because a computer's internal storage is finite, we can only store a fixed number of digits.
Now, observe that 3.14159 = 0.314159 × 10 = 0.314159 × 10¹
The standard internal representation (in a computer) is to store the digits "314159" and the exponent "1" (the power of 10 here), all of which takes less space.
This is called a floating point representation because we can adjust the exponent to make the decimal point "float"
Another example: 42.93 = 0.4293 × 10², which implies the digits "4293" and exponent "2".

Back to double:

The float format reserves a fixed number of spaces for digits.
This limits accuracy.
When you perform mathematical calculations with numbers represented in the float format, you can run into accuracy issues quickly.
This is why Java allows the accuracy to be doubled using double.

Hardly anyone uses float. anymore. We'll use double.

Homework 1: due Monday at midnight

Let's go through the first Homework 1 problems together now; there are a few additional details to how homework problems are scored that we should discuss together now, before you learn those pieces later this semester.

There are only five problems in the homework, but problems 2, 4, and 5 can be tricky! You should budget up to two hours for this assignment if you haven't programmed before. When you're working on the problems, stop after 20 minutes on a problem where you haven't made any progress, and create a post on Ed -- we answer these very quickly (usually less than an hour). While you're waiting, you can see if other people got stuck on the same problem (this will almost certainly happen!) and see if any of the answers there help you with your questions. Ed is the quickest and easiest way to receive help fast, and we love to answer your questions there!

Although this homework is graded, you are allowed (and encouraged!) to work in groups. You are also encouraged to help each other out on Ed, which includes getting class participation credit for answering someone else's question. We ask that if you are helping another student, you avoid just giving them your answer, as that doesn't help them learn as much as guiding them toward the correct answer does!

Activity 4: Let's solve Problem 0 on Homework 1 together, so we all understand how to run and use the driver.

Casting

Consider the following program:

Activity 5: What you suppose will be printed? Try it in an open visualizer window. Then, change the program to try the assignment the other way around: initially assign the value of 1 to i and then assign i to x.

An assignment from an int to a double works fine:

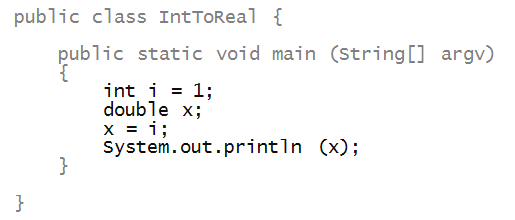
About casting:

The assignment from int to double works because every int is a valid double value.
However, a double need not be a valid int.
⇒ Which is why the compiler complains.
However, we can force an assignment using an explicit cast
The result: the largest integer less than the real.
⇒ The result is 1 above.
An explicit cast is need even if the double's value happens to be an integer like 1.0.
As we'll see later, casting is a general operation that can be applied to different variable types.

Activity 6: What do you get when you cast the real value 0.5 to an int? Write code in your Visualizer window to find out.

Next class:

Now that we understand basic numeric types, we'll learn how to tell a program to make a decision using conditional statements.
We will also continue with HW1 problems in lab this Thursday/Monday -- it is due Monday at 11:59pm.

Assignments for next lecture:

Complete all of the homework assignments on variables and numeric types before the next class (HW1 due Monday at 11:59pm), and prepare for the in-lecture quiz on lecture_04 notes on Tuesday.

CS 1111